微积分思维导图

对称性
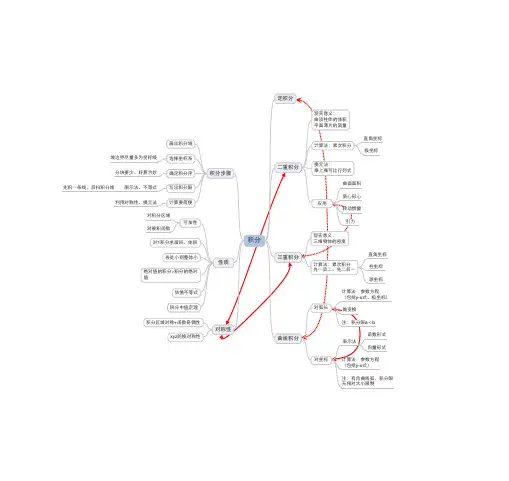
积分
定积分 二重积分 三重积分 曲线积分
现实意义： 曲顶柱体的体积 平面薄片的质量
计算法：累次积分
直角坐标 极坐标
换元法： 乘上雅可比行列式
应用
曲面面积 质心形心 转动惯量
引力
现实意义： 三维物体的密度
计算法：累次积分 先一后二、先二后一
直角坐标 柱坐标 球坐标
对弧长
计算法：参数方程 （包括y-x式、极坐标）
做变换
注：积分限a＜b
表示法函数形式ຫໍສະໝຸດ 向量形式对坐标计算法：参数方程 （包括y-x式）
注：有向曲线弧，积分限 无相对大小限制
画出积分域
域边界尽量多为坐标线
选择坐标系
分块要少、好算为妙
确定积分序
积分步骤
先积一条线，后扫积分域 图示法、不等式
写出积分限
利用对称性、换元法
计算要简便
对积分区域 对被积函数
可加性
对1积分求面积、体积
各处小则整体小
绝对值的积分>积分的绝对 值
性质
估值不等式
积分中值定理
积分区域对称+函数奇偶性 xyz轮换对称性