电阻对理想RLC串联谐振电路频率特性的影响

竭诚为您提供优质文档/双击可除rlc串联电路频率特性实验报告篇一：RLc串联电路的幅频特性与谐振现象实验报告_-_4(1)《电路原理》实验报告实验时间：20XX/5/17一、实验名称RLc串联电路的幅频特性与谐振现象二、实验目的1．测定R、L、c串联谐振电路的频率特性曲线。

2．观察串联谐振现象，了解电路参数对谐振特性的影响。

1．R、L、c串联电路(图4-1)的阻抗是电源频率的函数，即：Z?R?j(?L?1)?Zej??c三、实验原理当?L?1时，电路呈现电阻性，us一定时，电流达最大，这种现象称为串?c联谐振，谐振时的频率称为谐振频率，也称电路的固有频率。

即?0?1Lc或f0?12?LcR无关。

图4-12．电路处于谐振状态时的特征：①复阻抗Z达最小，电路呈现电阻性，电流与输入电压同相。

②电感电压与电容电压数值相等，相位相反。

此时电感电压(或电容电压)为电源电压的Q倍，Q称为品质因数，即Q?uLuc?0L11ususR?0cRRc在L和c为定值时，Q值仅由回路电阻R的大小来决定。

③在激励电压有效值不变时，回路中的电流达最大值，即：I?I0?usR3．串联谐振电路的频率特性：①回路的电流与电源角频率的关系称为电流的幅频特性，表明其关系的图形称为串联谐振曲线。

电流与角频率的关系为：I(?)?us1??R2??L???c??2?us0??R?Q2?0??I00??1?Q2?0?2当L、c一定时，改变回路的电阻R值，即可得到不同Q 值下的电流的幅频特性曲线(图4-2)图4-2有时为了方便，常以?I为横坐标，为纵坐标画电流的幅频特性曲线(这称?0I0 I下降越厉害，电路的选择性就越好。

I0为通用幅频特性)，图4-3画出了不同Q值下的通用幅频特性曲线。

回路的品质因数Q越大，在一定的频率偏移下，为了衡量谐振电路对不同频率的选择能力引进通频带概念，把通用幅频特性的幅值从峰值1下降到0.707时所对应的上、下频率之间的宽度称为通频带(以bw表示)即：bw??2?1??0?0由图4-3看出Q值越大，通频带越窄，电路的选择性越好。

在RLC串联谐振电路中，电阻R的作用非常重要：
1. 能量损耗：
电阻R代表了电路中的阻性成分，当电流通过时会产生热量，即造成能量损耗。

即使在谐振状态下，由于理想元件不存在，实际电路中的电阻也会导致部分电能转化为热能而损失掉。

2. 影响品质因数Q：
串联谐振电路的品质因数（Quality Factor, Q）是衡量系统对谐振频率响应选择性的参数。

其中，电阻的存在会降低Q值，意味着谐振电路的选择性变差，峰值电压降低，谐振曲线变得更宽。

3. 决定带宽：
在通信和信号处理领域，电阻与电感L和电容C 一起决定了电路的带宽。

在谐振条件下，带宽定义为谐振频率f0处增益下降到峰值增益的1/√2时的频率范围，电阻越大，带宽越宽。

4. 影响谐振峰值：
在谐振点，由于电阻的存在，会导致谐振时电路中
的电流不达到无限大，而是有一个最大值，这个最大电流受到电阻的影响。

5. 稳定性增强：
虽然电阻降低了效率和增大了带宽，但它也增加了电路的稳定性。

没有电阻的理想RLC谐振电路在发生谐振时可能出现非常大的电流或电压，这在某些情况下可能是危险的。

电阻的存在可以限制这些极端值。

总之，在RLC串联谐振电路中，电阻R虽然从效率角度看是一种不利因素，但它是电路设计中不可或缺的一部分，对于电路的工作特性、稳定性以及能源的有效利用等方面起着关键作用。

rlc串联谐振电路的工作原理RLC串联谐振电路是由电感、电阻和电容三个元件组成的电路。

它具有独特的工作原理和特性，常用于信号处理、滤波器设计、通信系统等领域。

我们来了解一下RLC串联谐振电路的基本组成。

电感是由线圈或绕组构成的元件，具有储存能量的特性。

电容则是由两个导体之间的绝缘介质隔开的元件，能够储存电荷。

电阻则是电流流过时产生的电压降的阻碍。

在RLC串联谐振电路中，电感、电容和电阻分别连接在串联的电路中。

当电路中的电感、电容和电阻达到一定的数值时，RLC串联谐振电路就会产生谐振现象。

谐振是指电路中的电感、电容和电阻的特定数值使得电路的阻抗最小，而电流和电压达到最大值的现象。

在RLC串联谐振电路中，电感和电容的谐振频率由以下公式决定：f = 1 / (2π√(LC))其中，f表示谐振频率，L表示电感的值，C表示电容的值，π是一个数学常数。

当外部输入信号的频率等于谐振频率时，电路中的电感和电容会产生共振现象。

此时，电感和电容会相互储存和释放能量，使得电流和电压达到峰值。

在RLC串联谐振电路中，电流和电压的相位差也是一个重要的特性。

在谐振频率附近，电流和电压的相位差接近0度，即它们几乎是同相的。

这是因为在谐振频率附近，电感和电容的阻抗相互抵消，电路的纯电阻部分占主导地位。

RLC串联谐振电路的工作原理可以通过以下过程来描述：1. 当外部输入信号的频率与谐振频率相差较大时，电路中的电感和电容的阻抗较大，电路的纯电阻部分起主导作用，电流和电压的幅值较小。

2. 当外部输入信号的频率与谐振频率接近时，电路中的电感和电容的阻抗减小，电路的纯电阻部分的影响减弱，电流和电压的幅值逐渐增大。

3. 当外部输入信号的频率等于谐振频率时，电路中的电感和电容的阻抗最小，电路的纯电阻部分几乎为零，此时电流和电压达到峰值。

4. 当外部输入信号的频率超过谐振频率时，电路中的电感和电容的阻抗又开始增大，电路的纯电阻部分起主导作用，电流和电压的幅值逐渐减小。

RLC串联电路的谐振特性研究实验报告.doc 实验目的：1. 了解RLC串联电路的工作原理及其谐振特性；2. 掌握测量RLC串联电路谐振频率和谐振带宽的方法。

实验仪器：1. RLC串联电路实验箱；2. 信号源；3. 示波器。

实验原理：RLC串联电路是由电阻、电感和电容串联形成的电路，它可以产生共振现象。

当其频率为共振频率时，电路中流过电流的大小取决于电路中的电感和电容。

此时，电路呈现出很高的阻抗，电流最大。

谐振频率 f0 由以下公式给出：f0 = 1 / (2π√LC)其中，L 为电路中的电感，C 为电路中的电容。

Z0 = R + j(XL - XC)谐振带宽 BW 的计算公式为：BW = Δf = f2 - f1其中，f1 和 f2 分别为电路总阻抗等于Z0/√2 时的频率。

实验步骤：1. 连接实验电路：将电阻、电感和电容串联起来，组成 RLC 串联电路，并连接信号源和示波器。

2. 设置信号源：将信号源的频率调节旋钮设置到最小值，同时将信号源电压调节旋钮调整到最大值。

3. 测量谐振频率：将示波器调节到 X-Y 模式，然后调节信号源频率调节旋钮，逐渐增大频率，直到示波器屏幕上显示出一个正弦波。

此时，记录下示波器显示的频率值，即为电路的谐振频率 f0。

实验结果：1. 在本次实验中，使用的电阻、电感和电容的值分别为：R = 1kΩ，L = 10mH，C = 0.1μF。

2. 在逐渐增大信号源频率的过程中，当频率达到 2231 Hz 时，电路中开始出现正弦波，此时记录下的频率值即为电路的谐振频率 f0。

3. 继续增大信号源频率，当频率达到 2358 Hz 时，电路总阻抗等于Z0/√2 时，记录下此时信号源频率调节旋钮的读数。

5. 通过计算，得到电路的谐振带宽为 157 Hz。

1. RLC串联电路可以产生共振现象，其频率为谐振频率 f0。

2. 对于给定的 RLC 串联电路，谐振频率 f0 取决于电路中的电感和电容的值。

rlc串联谐振电路研究实验报告RLC串联谐振电路研究实验报告引言：本文旨在研究RLC串联谐振电路的特性和性能。

RLC串联谐振电路是一种常见的电路结构，它由电阻（R）、电感（L）和电容（C）组成。

在特定频率下，RLC串联谐振电路能够表现出共振现象，这对于电子工程领域的应用具有重要意义。

实验目的：1. 研究RLC串联谐振电路的频率响应特性；2. 探究电阻、电感和电容对谐振频率和带宽的影响；3. 分析RLC串联谐振电路的相位差和频率之间的关系；4. 理解RLC串联谐振电路的功率传输和能量转换机制。

实验步骤：1. 搭建RLC串联谐振电路实验装置，包括电源、电阻、电感和电容等元件；2. 测量不同频率下电压和电流的数值；3. 绘制电压-频率和相位差-频率曲线，并找出谐振频率和带宽；4. 分析实验数据，总结RLC串联谐振电路的性能特点。

实验结果：通过实验测量和数据处理，我们得到了以下结果：在RLC串联谐振电路中，当输入信号频率等于谐振频率时，电路中的电流和电压达到最大值。

此时，电容的电压和电感的电流互相抵消，只有电阻消耗能量。

在谐振频率附近，电路的带宽较小，能够保持较高的品质因数。

而当频率远离谐振频率时，电路的电流和电压将会衰减。

讨论：通过实验数据和分析，我们可以得出以下结论：RLC串联谐振电路具有选择性放大特性，在谐振频率附近，电路能够对特定频率的信号进行放大，而对其他频率的信号进行衰减。

这种特性使得RLC串联谐振电路在无线通信、音频放大和滤波等领域有着广泛的应用。

实验结果还显示，电阻、电感和电容对RLC串联谐振电路的性能有着重要影响。

电阻的增加会减小电路的品质因数，降低谐振频率和带宽；电感值的增加会提高电路的品质因数，增大谐振频率和带宽；而电容的变化则会对谐振频率产生较大影响。

结论：通过本次实验，我们深入了解了RLC串联谐振电路的特性和性能。

该电路在电子工程领域具有重要应用，能够对特定频率的信号进行放大和滤波。

R、L、C串/并联谐振电路的特性分析及应用摘要：本文对RLC串联、RLC并联及RL-C并联三种谐振电路的阻抗Z、谐振频率 、及品质因数Q三种特性进行了分析。

其中品质因数Q是电路在谐振状态下最为重要的电路特性，我们从Q的几种定义出发，着重研究了它对三种最基本的谐振电路的几个重要影响。

同时简单介绍了串/并联谐振电路在生活中的具体应用。

关键词：谐振电路；谐振特性；品质因数目录0 引言： (1)1 RLC串联与RLC并联及RL-C并联电路阻抗及谐振频率 (2)1.1 RLC串联电路的阻抗及谐振频率 (2)1.2 RLC并联电路的阻抗及谐振频率 (2)1.3 RL-C并联电路的阻抗及谐振频率 (3)2 R、L、C串/并联电路的品质因数Q (3)2.1 电路的品质因数Q (3)2.2 谐振电路的品质因数Q的几点重要性 (4)2.2.1 Q对回路中能量交换及能量储存的影响 (4)2.2.2 Q值与谐振电路的选择性 (4)2.2.2.1 Q值与串联谐振电路的选择性 (4)2.2.2.2 Q值与RL-C并联谐振电路的选择性 (6)2.2.2.3 RLC并联谐振回路与RL-C并联谐振回路的品质因数的统一性 (8)3 谐振电路在生活中的应用 (11)0 引言：构成各种复杂电路的基础通常是RLC 串/并联谐振电路，本文就简单介绍了其三种连接方式如图，而了解这些基本电路的频率特性对于理解更复杂的电路甚至实用电路是非常有益的,并且对于深入了解其它重要的相关特性是十分有帮助的。

本文简单阐述了下面三种电路图的Z 、ω及Q 以及一些具体实际的应用。

下面是R 、L 、C 串/并联谐振电路的简图，如图1，图2，图3所示。

•R U•L U＋•U•C U图1,串联谐振电路RLC•U— 图2，并联谐振电路RLC图3,并联谐振电路C RL -1 RLC 串联与RLC 并联及RL-C 并联电路阻抗及谐振频率 1.1 RLC 串联电路的阻抗及谐振频率由图1知RLC 串联电路的复阻抗Z 和阻抗z 分别为()()22111CL R z L L j R C jL j R Z ωωωωωω-+=-+=-+=电路中的I 和z 以及U 之间的关系为：()221CL R U zU I ωω-+==(1)由于谐振时01=-C L ωω，故谐振时的电流 R U I I =00为。

rlc串联谐振电路的实验报告实验报告：RLC串联谐振电路引言：RLC串联谐振电路是电工学中常见的一种电路，它由电感器（L）、电容器（C）和电阻器（R）组成。

在特定的频率下，串联谐振电路能够表现出一系列特殊的性质和行为。

本实验旨在通过搭建RLC串联谐振电路并进行实验，进一步研究和探索其特性和应用。

一、实验装置与原理1. 实验装置：本实验所需的装置包括：信号发生器、电感器、电容器、电阻器、示波器、万用表等。

2. 实验原理：RLC串联谐振电路是由电感器、电容器和电阻器依次连接而成。

当电路中的电感、电容和电阻分别为L、C和R时，串联谐振电路的共振频率f0可由以下公式计算得出：f0 = 1 / (2π√(LC))二、实验步骤1. 搭建电路：根据实验要求，按照串联谐振电路的连接方式，将电感器、电容器和电阻器依次连接起来。

2. 调节信号发生器：将信号发生器连接到电路中，调节信号发生器的频率，使之逐渐接近共振频率f0。

3. 观察示波器波形：将示波器连接到电路中，调节示波器的设置，观察电路中的电压波形。

当信号发生器的频率接近共振频率f0时，示波器上的波形将出现明显的共振现象。

4. 测量电压和电流：使用万用表等测量工具，分别测量电感器、电容器和电阻器上的电压和电流数值。

三、实验结果与分析通过实验，我们得到了一系列数据，并进行了进一步的分析和研究。

1. 共振频率：根据实验测量的数据，我们计算得到了串联谐振电路的共振频率f0。

与理论计算值进行对比，可以评估实验的准确性和可靠性。

2. 波形分析：观察示波器上的波形，我们可以看到在共振频率f0附近，电压波形呈现出明显的共振现象。

这是因为在共振频率下，电感器和电容器的阻抗相互抵消，电路中的电流达到最大值。

3. 电压和电流的关系：通过测量电路中电压和电流的数值，我们可以进一步分析电压和电流之间的关系。

根据欧姆定律和基尔霍夫电压定律，我们可以推导出电流与电压的相位差等相关参数。

四、实验应用与展望RLC串联谐振电路在实际应用中具有广泛的用途，例如：1. 滤波器：串联谐振电路可以用作滤波器，通过调节频率可以选择性地滤除或通过特定频率的信号。

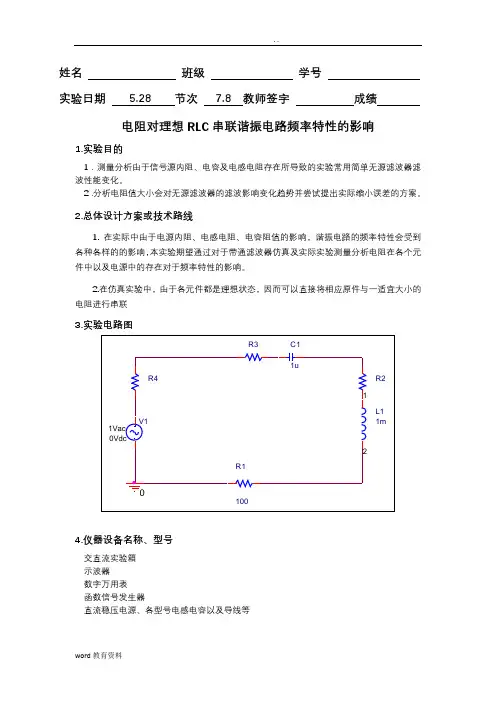
姓名班级学号实验日期 5.28 节次7.8 教师签字成绩电阻对理想RLC串联谐振电路频率特性的影响1.实验目的1．测量分析由于信号源内阻、电容及电感电阻存在所导致的实验常用简单无源滤波器滤波性能变化。

2．分析电阻值大小会对无源滤波器的滤波影响变化趋势并尝试提出实际缩小误差的方案。

2.总体设计方案或技术路线1. 在实际中由于电源内阻、电感电阻、电容阻值的影响，谐振电路的频率特性会受到各种各样的的影响，本实验期望通过对于带通滤波器仿真及实际实验测量分析电阻在各个元件中以及电源中的存在对于频率特性的影响。

2.在仿真实验中，由于各元件都是理想状态，因而可以直接将相应原件与一适宜大小的电阻进行串联3.实验电路图4.仪器设备名称、型号交直流实验箱示波器数字万用表函数信号发生器直流稳压电源、各型号电感电容以及导线等5.电感内阻电容内阻Frequency V(R2:1)+ V(C1:1)FrequencyV(R2:1)+ V(L1:1)电阻增加V(R1:1)Frequency电源内阻其中所有电阻变化在图线下标中均为从左向右依次增加，第一个为1nΩ，模拟0内阻的时候，其余四个为10Ω，100Ω，1kΩ，10kΩ6.详细实验步骤及实验结果数据记录（包括各仪器、仪表量程及内阻的记录）测量电源内阻影响1.按照电路图连接电路，并检查个部分工作是否正常。

2.对电源进行串连一个电阻箱，并调节相应电阻值。

3.调节信号源频率，使获得最大信号强度，记录此时频率f0。

4.在此频率基础上测量获得两个截止频率，并在其中选取相应频率值记数。

5.改变电阻值，再次测量。

信号源频率/Hz 10 80 149 180 210 f0 223 输出电压/mv 30.9 266 582 726 810 821信号源频率/Hz 260 310 340 400 1k 电阻值Ω输出电压/mv 777 652 581 469 160 0 信号源频率/Hz 10 40 144 170 210 f0 223 输出电压/v 30.9 126 536 645 750 758信号源频率/Hz 270 290 352 500 2k 电阻值Ω输出电压/v 705 663 535 349 77.1 100 信号源频率20 80 110 150 190 f0 223/Hz输出电压/v 61.8 239 316 394 437 446信号源频率/Hz 280 340 464 600 1k 电阻值Ω输出电压/v 430 392 315 251 155 1k相应修正:信号源电压Vrms=1v，C=5uF，L=1H，Rl=146Ω测量电感内阻影响1.按照电路图连接电路，并检查个部分工作是否正常。

实验报告祝金华 PB 实验题目：R 、L 、C 串联谐振电路的研究实验目的： 1. 学习用实验方法绘制R 、L 、C 串联电路的幅频特性曲线;2. 加深理解电路发生谐振的条件、特点,掌握电路品质因数电路Q 值的物理意义及其测定方法;实验原理 1. 在图1所示的R 、L 、C 串联电路中,当正弦交流信号源U i 的频率 f 改变时,电路中的感抗、容抗随之而变,电路中的电流也随f 而变; 取电阻R 上的电压U O 作为响应,当输入电压U i 的幅值维持不变时, 在不同频率的信号激励下,测出U O 之值,然后以f 为横坐标,以U O 为纵坐标,绘出光滑的曲线,此即为幅频特性曲线,亦称谐振曲线,如图2所示;图22. 在f ＝fo ＝LCπ21处,即幅频特性曲线尖峰所在的频率点称为谐振频率;此时X L＝Xc,电路呈纯阻性,电路阻抗的模为最小;在输入电压U i 为定值时,电路中的电流达到最大值,且与输入电压U i 同相位;从理论上讲,此时 U i ＝U R ＝U O ,U L ＝U c ＝QU i ,式中的Q 称为电路的品质因数;3. 电路品质因数Q 值的两种测量方法 一是根据公式Q ＝oCU U 测定,U c 为谐振时电容器C 上的电压电感上的电压无法测量,故不考虑Q=oLU U 测定 ;另一方法是通过测量谐振曲线的通频带宽度△f ＝f2－f1,再根据Q ＝12f f f O-求出Q 值;式中f o 为谐振频率,f 2和f 1是失谐时, 亦即输出电压的幅度下降到最大值U 0102Li图 1的2/1 ＝倍时的上、下频率点;Q 值越大,曲线越尖锐,通频带越窄,电路的选择性越好; 在恒压源供电时,电路的品质因数、选择性与通频带只决定于电路本身的参数,而与信号源无关;预习思考题1. 根据实验线路板给出的元件参数值,估算电路的谐振频率;L=30mH fo ＝LCπ21=1/2×π631001.01030--⨯⨯⨯=2. 改变电路的哪些参数可以使电路发生谐振,电路中R 的数值是否影响谐振频率值改变频率f,电感L,电容C 可以使电路发生谐振,电路中R 的数值不会影响谐振频率值; 3. 如何判别电路是否发生谐振测试谐振点的方案有哪些 4.判断：电容与电感的电压相等时,电路此时发生谐振；U i 与U 0相位相同时此时发生谐振；U i 与U 0大小相等时电路发生谐振; 测量：理论计算,f=1/2π√LC；仪表测量此时电流频率;4． 电路发生串联谐振时,为什么输入电压不能太大, 如果信号源给出3V 的电压,电路谐振时,用交流毫伏表测U L 和U C ,应该选择用多大的量限输入电压过大,L 、C 器件两端的电压远高于信号源电压；应该选用最大量程 ; 5. 要提高R 、L 、C 串联电路的品质因数,电路参数应如何改变减小R,增大L,同时等比例缩小C; 6. 本实验在谐振时,对应的U L 与U C 是否相等如有差异,原因何在7.U L ,U C 大小相等,方向相反,因为在谐振点L,C 的阻抗相等,二者阻抗方向相反;实验设备低频函数信号发生器,交流毫伏表,双踪示波器,频率计,谐振电路实验电路板 实验内容1. 利用HE-15实验箱上的“R 、L 、C 串联谐振电路”,按图3组成监视、测量电路;选C 1=μF;用交流毫伏表测电压, 用示波器监视信号源输出;令信号源输出电压U i =3V ,并保持不变;图 32. 找出电路的谐振频率f0,其方法是,将毫伏表接在R200Ω两端,令信号源的频率由小逐渐变大注意要维持信号源的输出幅度不变,当Uo的读数为最大时,读得频率计上的频率值即为电路的谐振频率f0,并测量U C与U L之值注意及时更换毫伏表的量限;3. 在谐振点两侧,按频率递增或递减300Hz或500KHz,依次各取8 个测量点,逐点测出②U i=3v, C=μF, R=200Ω, f o= , f2-f1= , Q==数据处理1. 根据测量数据,绘出不同Q值时三条幅频特性曲线,即：U O＝UfU c=Uf2. 计算出通频带与Q 值根据输出电压与输入信号频率的记录,可得f 0=③ f 2-f 1= , Q== ②Q=U C /U 0==实验总结和误差分析对两种不同的测Q 值的方法进行比较,分析误差原因; 第一种方法测量出的Q 值偏大,由公式Q=12f f f O-计算时,由于实验仪器精度并不是非常小,存在一定的仪器误差和读数误差,f 0课确定范围较大,且由图像读数f 1,f 2也不是非常精确,不确定度较大;第二种方法测量Q 值时,由于频率在一定范围内电阻电压保持最大值,无法精确确定f 0,导致U 0、U C 可选范围增大,Q 值可取值增多;谐振时,比较输出电压U O 与输入电压U i 是否相等 试分析原因;不相等,电感并不是理想电感,存在电阻,导线存在电阻,消耗电压;通过本次实验,总结、归纳串联谐振电路的特性;①在f ＝fo ＝LCπ21处,即幅频特性曲线尖峰所在的频率点为谐振频率时,X L＝Xc,电路呈纯阻性,电路阻抗的模为最小,等于电阻阻值;②在输入电压U i 为定值时,电路中的电流达到最大值,且与输入电压U i 同相位; ③电阻电压也达到最大值;④电感和电容的电压也达到最大,且是反相位;心得体会及其它1. 第一次做电工实验,对实验器材、实验步骤存在疑问,应该主动预先预习,了解相关知识;2. 电压的测量问题中,应该考虑向电路接入毫伏表对电路的影响,注意各个表笔接地端是否产生短路3. 对于实验安全,应该遵守实验室规则,听从老师的安排,不随意行动;4. 信号发射器关于频率的调节,应该先粗调,后细调;。

RLC 串联谐振电路实验误差的分析及改进一、摘要：从RLC 串联谐振电路的方程分析出发，推导了电路在谐振状态下的谐振频率、品质因数和输入阻抗，并且基于Multisim仿真软件创建RLC 串联谐振电路，利用其虚拟仪表和仿真分析，分别用测量及仿真分析的方法验证它的理论根据。

其结果表明了仿真与理论分析的一致性，为仿真分析在电子电路设计中的运用提供了一种可行的研究方法。

二、关键词：RLC；串联；谐振电路；三、引言谐振现象是正弦稳态电路的一种特定的工作状态。

通常，谐振电路由电容、电感和电阻组成，按照其原件的连接形式可分为串联谐振电路、并联谐振电路和耦合谐振电路等。

由于谐振电路具有良好的选择性，在通信与电子技术中得到了广泛的应用。

比如，串联谐振时电感电压或电容电压大于激励电压的现象，在无线电通信技术领域获得了有效的应用，例如当无线电广播或电视接收机调谐在某个频率或频带上时，就可使该频率或频带的信号特别增强，而把其他频率或频带的信号滤去，这种性能即称为谐振电路的选择性。

所以研究串联谐振有重要的意义。

在含有电感L 、电容C 和电阻R 的串联谐振电路中，需要研究在不同频率正弦激励下响应随频率变化的情况，即频率特性。

Multisim 仿真软件可以实现原理图的捕获、电路分析、电路仿真、仿真仪器测试等方面的应用，其数量众多的元件数据库、标准化仿真仪器、直观界面、简洁明了的操作、强大的分析测试、可信的测试结果都为众多的电子工程设计人员提供了一种可靠的分析方法，同时也缩短了产品的研发时间。

四、正文（1）实验目的：1.加深对串联谐振电路条件及特性的理解。

2.掌握谐振频率的测量方法。

3.理解电路品质因数的物理意义和其测定方法。

4.测定RLC串联谐振电路的频率特性曲线。

(2)实验原理：RLC串联电路如图所示，改变电路参数L、C或电源频率时，都可能使电路发生谐振。

该电路的阻抗是电源角频率ω的函数：Z=R+j(ωL-1/ωC)当ωL-1/ωC=0时，电路中的电流与激励电压同相，电路处于谐振状态。

C1L ω=ωfC 21πC1ωLC21πLC1LC实验八 R 、L 、C 串联电路的谐振实验一、实验目的1、研究交流串联电路发生谐振现象的条件。

2、研究交流串联电路发生谐振时电路的特征。

3、研究串联电路参数对谐振特性的影响。

二、实验原理1、R L C 串联电压谐振在具有电阻、 电感和电容元件的电路中，电路两端的电压与电路中的电流一般是不同相的。

如果我们调节电路中电感和电容元件的参数或改变电源的频率就能够使得电路中的电流和电压出现了同相的情况。

电路的这种情况即电路的这种状态称为谐振。

R 、L 、C 串联谐振又称为电压谐振。

在由线性电阻R 、电感L 、电容c 组成的串联电路中，如图8-1所示。

图8-1 R L C 串联电路图当感抗和容抗相等时，电路的电抗等于零即X L = X C ； ； 2πf L=X = ω L － = 0则 ϕ = arc tg = 0即电源电压u 与电路中电流i 同相，由于是在串联电路中出现的谐振故称为串联谐振。

谐振频率用f 0表示为f = f 0 = 谐振时的角频率用ω 0表示为ω = ω 0 =谐振时的周期用T 0表示为T = T 0 = 2 π 串联电路的谐振角频率ω 0频率f 0，周期T 0，完全是由电路本身的有关参数来决定的，它们是电路本身的固有性质，而且每一个R 、L 、C 串联电路，只有一个对应的谐振频f 0和 周期T 0。

因而，对R 、L 、C 串联电路来说只有将外施电压的频率与电路的谐振频率相等时候，电路才会发生谐振。

在实际应用中，往往采用两种方法使电路发生谐振。

一种是当外施()2CL2X X R -+RU UU U电压频率f 固定时，改变电路电感L 或电容C 参数的方法，使电路满足谐振条件。

另一种是当电路电感L 或电容C 参数固定时，可用改变外施电压频率f 的方法，使电路在其谐振频率下达到谐振。

总之，在R 、L 、C 串联电路中，f 、L 、C 三个量，无论改变哪一个量都可以达到谐振条件，使电路发生谐振。

RC 、RL 及RLC 串联电路幅频和相频特性的研究【摘要】本文主要研究RC ，RL 和RLC 串联电路在不同频率的信号下的响应，在双踪示波器上同时观察电阻和电感（或电容）上输出电压幅度和相位差的变化，定量研究了RLC 串联电路的幅频特性和相频特性。

同时发现在实际的实验操作中，电阻，电容以及电感的参数的选择对本实验有很大的影响，掌握了幅频特性和相频特性的测量方法，使理论知识和实验内容有机的结合起来。

【关键词】串联电路；RLC 电路；相频特性；幅频特性 1引言RC 、RL 和RLC 串联电路是大学物理实验的设计性实验之一，在交流电路中，幅频特性和相频特性是RC 、RL 和RLC 串联电路的重要性质，并在电子电路中被广泛应用。

本文对实验方法进行改进，采用幅频和相频特性的测量方法，观察各种参数变化，进一步了解各种参数对幅频特性和相频特性的影响。

2实验设计原理在RC ，RL ，RLC 串联电路中， 若加在电路两端的正弦交流信号保持不变，则当电路中的电流和电压变化达到稳定状态时，电流（或者某元件两端的电压）与频率之间的关系特性称为幅频特性；电压、电流之间的位相差与频率之间的关系特性称位相频特性。

2.1 RC 串联电路电路如图1所示。

令ω表示电源的圆频率，U ，I ，R U ,C U 分别表示电源电压，电路中的电流，电阻R 上的电压和电容C 上的有效值。

ϕ表示电路电流I 和电源电压U 间的相位差，则： RC 总阻抗为：CjR Z ω1~-= （1） 其中Z ~的模为：221|~|⎪⎭⎫ ⎝⎛+==C R Z Z ω（2）CR R Cωωϕ1arctan 1arctan -=⎪⎪⎪⎪⎭⎫ ⎝⎛-= （3）ϕ为U 和I 之间的相位差，即 I U ϕϕϕ-= （4）RL 的总阻抗为：L j R Z ω+=~（10） 其模为：()22|~|L R Z Z ω+== （11）其辐角为：RLωϕarctan= （12） IR U R = (13)L I U L ω= (14) 22)(L R IU ω+= (15)图4图5图52.2.2相频特性图6 图7由式（12）和图7可知：从0逐渐增大并趋近于∞时，相应的8所示，不同于RC和RL电路：图8调节函数发生器的频率在f=100～3000之间，实个不同的频率点，用示波器分别测量电阻和电感的峰峰值电压R U 图10 RLC 实验装置参数的选择对本实验有很大的影响，不合适的元件参数下实验现象会出现不稳定，不明显甚至无法观察，这是实验时应当注意的。

一、概述1.1 RLC串联电路的基本结构和特性1.2 频率与响应对RLC串联电路的影响二、RLC串联电路频率与响应之间的关系2.1 频率对电阻的影响2.2 频率对电感的影响2.3 频率对电容的影响三、频率对RLC串联电路整体响应的影响3.1 阻抗角和相位差3.2 谐振频率和带宽3.3 激励信号频率选择与响应分析四、频率与RLC串联电路的应用4.1 通信与信号处理4.2 滤波器设计4.3 可变频率电路设计五、结论5.1 频率与RLC串联电路的紧密关系5.2 频率与响应的深入研究对工程应用的重要性本文将通过对RLC串联电路频率与响应之间的关系展开论述。

首先简要介绍RLC串联电路的基本结构和特性，然后重点分析频率对电阻、电感和电容的影响。

接着探讨频率对RLC串联电路整体响应的影响，包括阻抗角和相位差、谐振频率和带宽等方面的讨论。

本文将介绍频率对RLC串联电路在通信、信号处理、滤波器设计和可变频率电路设计等领域的应用，并总结频率与RLC串联电路的紧密关系以及对工程应用的重要性。

一、概述1.1 RLC串联电路的基本结构和特性RLC串联电路是由电阻、电感和电容三种基本元件按一定顺序连接而成的电路。

电阻R阻碍电流的通过，电感L对电流的变化很敏感，电容C则对电压变化具有很大的响应。

根据基尔霍夫定律和欧姆定律，RLC串联电路中，电感和电容对电压和电流具有相位差，而电阻对电压和电流没有相位差。

具体来说，电阻和电容的电压和电流是同相的，而电感的电压和电流是异相的。

1.2 频率与响应对RLC串联电路的影响在工程实际应用中，RLC串联电路频率与其响应之间的关系是一个重要的研究课题。

频率是指单位时间内信号波形的重复率，是变化的速度。

对于RLC串联电路来说，频率会直接影响电感和电容的阻抗，并对整个电路的响应产生影响。

以下将分别讨论频率对电阻、电感和电容的影响。

二、RLC串联电路频率与响应之间的关系2.1 频率对电阻的影响对于电阻来说，频率对其阻抗没有影响。

rlc串联谐振电路阻抗
（最新版）
目录
1.RLC 串联谐振电路的概念
2.RLC 串联谐振电路的阻抗特性
3.RLC 串联谐振电路的谐振频率
4.RLC 串联谐振电路的应用
正文
一、RLC 串联谐振电路的概念
RLC 串联谐振电路是一种由电阻（R）、电感（L）和电容（C）串联组成的电路。

当电路中的电阻、电感和电容满足特定条件时，电路会发生谐振现象，即电路中的电流和电压呈现周期性变化。

在 RLC 串联谐振电路中，阻抗最小，电流最大。

二、RLC 串联谐振电路的阻抗特性
在 RLC 串联谐振电路中，当电路发生谐振时，电路的总阻抗等于纯电阻值，即阻抗最小。

这是因为在谐振状态下，电感和电容的电压相位相反，相互抵消，从而使得电路的总阻抗最小。

三、RLC 串联谐振电路的谐振频率
RLC串联谐振电路的谐振频率可以通过公式1/(2π√(LC))计算。

其中，L表示电感，C表示电容。

在谐振频率处，电路的阻抗最小，电流最大。

四、RLC 串联谐振电路的应用
RLC 串联谐振电路在电子工程中有广泛的应用，如无线通信、广播电视、音响设备等领域。

在通信领域，RLC 谐振电路常用于制作滤波器、振
荡器等；在广播电视领域，RLC 谐振电路用于制作电视信号发生器；在音响设备中，RLC 谐振电路用于制作扬声器等。

总之，RLC 串联谐振电路是一种具有特殊阻抗特性和谐振频率的电路，广泛应用于电子工程领域。

rlc串联谐振电路阻抗
（最新版）
目录
1.RLC 串联谐振电路的概念
2.RLC 串联谐振电路的阻抗特性
3.RLC 串联谐振电路的谐振频率
4.RLC 串联谐振电路的应用
正文
一、RLC 串联谐振电路的概念
RLC 串联谐振电路是一种由电阻（R）、电感（L）和电容（C）串联组成的电路，它是一种特殊的电路，能够在特定频率下产生谐振现象。

在 RLC 串联谐振电路中，电阻、电感和电容共同作用，使得电路的阻抗在某一频率下达到最小值。

二、RLC 串联谐振电路的阻抗特性
在 RLC 串联谐振电路中，当电路发生谐振时，电路的阻抗达到最小值。

此时，电路中的电流最大。

阻抗的大小取决于电路中的电感、电容和电阻的数值，可以通过计算得到。

在 RLC 串联谐振电路中，阻抗的计算公式为：Z = R + j(ωL - 1/ωC)，其中，Z表示阻抗，R表示电阻，ω表示角频率，L表示电感，C表示电容。

三、RLC 串联谐振电路的谐振频率
RLC 串联谐振电路的谐振频率可以通过公式 f = 1/(2π√(LC))计算得到。

在这个公式中，f表示谐振频率，L表示电感，C表示电容。

当电路的频率等于谐振频率时，电路的阻抗最小，电流最大。

四、RLC 串联谐振电路的应用
RLC 串联谐振电路在电子工程中有广泛的应用，例如在无线通信、广播电视、计算机网络等领域都有应用。

此外，RLC 串联谐振电路还可以用于制作滤波器、振荡器等电子设备。

谐振频率电阻
谐振频率和电阻是电路中非常重要的两个参数。

谐振频率是指当电路中的电感和电容元件形成共振时的频率，而电阻则是电路中的阻力。

谐振频率和电阻的关系非常密切，因为它们共同影响着电路的性能和特性。

在电路中，电感和电容元件可以组合成不同类型的谐振电路，如串联谐振电路和并联谐振电路等。

这些电路的谐振频率取决于电容和电感值的大小，以及电路中的电阻值。

当电路中的电阻值很小时，谐振频率会相对较高，而当电路中的电阻值较大时，谐振频率则会较低。

电阻对电路的影响相当重要，因为它可以影响电路中的能量损耗和信号幅度。

在某些情况下，电路中需要加入一定的电阻来控制电路的电流和电压等参数，从而达到所需的功能。

例如，在滤波器电路中，加入一定的电阻可以增强滤波效果，使电路的输出信号更加纯净。

总之，谐振频率和电阻是电路中不可或缺的两个参数，它们共同作用着电路的性能和特性。

在设计和应用电路时，需要充分考虑谐振频率和电阻对电路的影响，从而达到最佳的性能和效果。

- 1 -。

rlc串联谐振电路截止频率RLC串联谐振电路是一种在电子学中被广泛应用的电路。

它具有一个共振频率，在这个频率点上，电路的串联阻抗达到最小值，同时电路中的谐振电流达到最大值。

本文将讨论RLC串联谐振电路中的截止频率，这是一个非常重要的概念，它是指在串联谐振电路中，当频率超出一定的范围时，谐振电路将不能正常工作。

我们将探讨这个频率是如何确定的，它的物理原理和应用。

在RLC串联谐振电路中，R、L和C分别代表电阻、电感和电容。

电导性质与电阻在概念上是一致的，所以在后续的讨论中，我们将使用“电阻”一词代替“电导”。

在这种电路中，电感和电容通过电导连接。

两者的共同作用是使电路中的电流呈现出谐振的特性。

谐振电路的共振频率是什么？共振频率是指当电路中电感和电容的共同作用下，电路的串联阻抗达到最小值所对应的频率。

在这个频率点上，电阻的影响非常小，因为在它附近，只有电感和电容能够影响电路阻抗。

在这种情况下，电路中的谐振电流达到最大值。

然而，在共振频率两侧的频率范围内，电路的阻抗将发生变化。

当频率降低时，电感的作用变得更加明显，阻抗将上升。

同样的，当频率增加时，电容的作用更加明显，电路阻抗也会上升。

当频率超出一定范围时，电路的阻抗将变得非常高，阻止电流继续流动，从而产生所谓的截止现象。

这个频率就是截止频率。

当电路的频率达到截止频率时，电路的阻抗将变得非常大，任何外置的电流将无法通过电路。

这是由于在这个频率点上，电路中电感和电容的阻抗相互抵消，使电路中的电阻成为主导因素。

因此，当电路的频率超出截止频率时，电路将无法表现出谐振的特性。

在实际应用中，截止频率非常重要。

它是系统中的一个安全保护，可以避免系统中产生过多的谐振干扰。

在设计电路时，我们需要确保电路的工作频率不会超出截止频率范围，从而保证电路能够正常工作。

同样的，由于在截止频率下，阻抗非常大，电路可以作为合适的高通滤波器使用。

通过对电路的频率进行调整，我们能够在谐振电路中加入不同的滤波效果，达到预期的目的。