当前位置：文档之家 › 复变函数同步辅导及习题全解-西安交大版下

复变函数同步辅导及习题全解-西安交大版下

  • 格式：pdf
  • 大小：1.99 MB
  • 文档页数：134

下载文档原格式

  / 134

合集下载

西安交大西工大 考研备考期末复习 工程数学复变函数 复数与复变函数

西安交大西工大 考研备考期末复习 工程数学复变函数 复数与复变函数
z r cos i sin
z rei
三角表达式 指数表达式
说明： z r cos i sin
rei
复变函数
例1.将下列复数写为三角表达式与指数表达式
1)z 12 2i
2)z sin i cos
5
5
3)z 1 cos i sin
0
例2.求证 z1 z2 z1 z2
z2
x22 y22
复变函数
2.复数的运算法则
z1 z2 z2 z1, z1z2 z2 z1
(交换律)
z1 z1
(z2 z3) (z1 (z2 z3 ) (z1z2 )z3
z2
)
z3
(结合律)
z1(z2 z3 ) (z1z2 z1z3 ) (分配律)
复变函数
3.共轭复数
2k
n
其中 k 0,1, , n 1
例2.求 1) 1 i 6
2) 6 1
复变函数
本次课小结 本次课的内容要点
1.复数的概念 2.复数的代数运算 3.复数的几何表示 4.复数的乘幂与方根
作业：习题一 4(4)、8(1,3,6)、11 14(3、4)、16、21(4、6)
复变函数
说明：1) z 0 若z=0，则辐角不定
2） tan y ，即tan Argz y
x
x
3) 多值性 Argz 2k
4) 把满足 的辐角称为辐角主值
记为 arg z
arg z arctan y x
复变函数
arg z arctan y
x
arg z arctan y
x
arg z arctan y x
复变函数
复变函数的理论基础是在十九世纪奠定的，主 要是围绕柯西 、魏尔斯特拉斯和黎曼三人的工作进 行的。

《复变函数》(西安交大 第四版)第7章 拉普拉斯变换

《复变函数》(西安交大 第四版)第7章 拉普拉斯变换
f (t T ) f (t) (t 0)
当 f (t)在一个周期上连续或分段连续时,则有
ℒ
f
(t)
1
1 es
T
T f (t)es tdt
0
这是求周期函数拉氏变换公式
例8 设f (t)是以2 为周期的函数，且在一个
周期内 的表达式 为f (t)
cos
0
t
0
t t
2
求: ℒ f (t)
est dt
k
k2
sin k t estdt
0
s2 s2 0
所以
sin
k
t
s2
k
k2
Res 0
即
k sin kt s2 k 2 (Re(s) 0)
同理可得
cos kt
s s2 k2
(Re(s) 0)
如
ℒ
sin
2t
s2
2
4
Res 0
ℒ
cos
3t
s2
s
9
Res 0
例7 求: f (t) e t (t) e tu(t) ( 0)
函数可写为 F(s) f (t) estdt 0
我们称上式为函数 f (t)的拉普拉斯变换式 ,记做
F (s) ℒ f (t)
F(s) 叫做 f (t) 的拉氏变换,象函数.
f (t) 叫做 F(s) 的拉氏逆变换,象原函数,f (t) =ℒ 1 F(s)
7.1.2 拉普拉斯变换存在定理
d ds
s2
s
k
2
s2 k2 s2 k2 2
例13 求: f (t) te t cos t 的Laplace变换。

复变函数西安交大 第四版第六讲PPT课件

复变函数西安交大 第四版第六讲PPT课件
---级数的部分和
▪ 若z0 D ln i m sn (z0 ) s(z0 ),称 级 数(1)在z0收 敛, 其 和 为s(z0 ), ln i m sn (z0 )不 存 在 ， 称 级 数(1)在z0发 散 。
且
u u ( ) ( )
y y x x
v x
dx
v y
dy
u y
dx
u x
dy
v
d v(
x,
y)
( x, y)
u
u
v(x, y)
( dx dy) c ()
y ( x0 , y0 )
x
第7页/共47页
v u v u 满 足C R方 程. x y y x
u iv在D内 解 析.
n0 n! n0 n!
n0 n!
(3)
n1
(1)n
收
敛
，
n
n1
1 2n
收
敛
，
n1
(
(1)n n
i 2n
)收 敛.
又 (1)n 条 件收 敛，原 级数 非 绝对 收 敛. n1 n
第24页/共47页
例3
讨论
z
n
的
敛散性。
n0 n!
解
令 z r,
zn
rn er
n0 n! n0 n!
1. 复数列的极限 2. 级数的概念
第17页/共47页
1. 复数列的极限
定义 设复数列{：n}(n 1,2,),其中n＝an ibn,
又设复常数： a ib，
若 0, N 0, n N , 恒 有n ，
那 么称 为 复 数 列{n }当n 时 的 极 限 ，
记

西安交大复变函数课件5-1-1本性奇点

西安交大复变函数课件5-1-1本性奇点
sinh z 思考 z 0 是 3 的几级极点? z
注意: 不能以函数的表面形式作出结论 .
21
三、函数在无穷远点的性态
1. 定义 如果函数 f (z ) 在无穷远点 z 的去心 邻域 R z 内解析, 则称点 为 f (z ) 的孤 y 立奇点. R o
x
22
1 1 (t ), 令变换 t : 则 f ( z ) f 规定此变换将: z t 映射为 z t 0,
z
ez 1 z 因为 lim lim e 1, z 0 z 0 z
8
2. 极点 1) 定义 如果洛朗级数中只有有限多个 z z0 的
负幂项, 其中关于 ( z z0 ) 的最高幂为 ( z z0 ) , 即
1
m
f ( z ) cm ( z z0 ) c2 ( z z0 ) c1 ( z z0 )
3
孤立奇点的分类 依据 f (z ) 在其孤立奇点 z0 的去心邻域
0 z z0 内的洛朗级数的情况分为三类:
1．可去奇点;
1．可去奇点
2．极点;
3．本性奇点.
1) 定义 如果洛朗级数中不含 z z0 的负幂项,
那末孤立奇点 z0 称为 f (z ) 的可去奇点.
4
说明: (1) z0若是f ( z )的孤立奇点 ,
c0 c1 ( z z0 )
m
2
1
( m 1, cm 0)
1 1 f ( z )f z ) m g ( z) , ggz)z ) , 0处解析,且g ( z0 ) 0 ( ( 在z ( (z z ) 或写成 0 ( z z )m
0

西安交大工程数学复变函数第四版第三章复变函数的积分

西安交大工程数学复变函数第四版第三章复变函数的积分

显然曲线 AEBBEAA,AAFBBFA均为封闭曲线.
因为它们的内部全含于D,
故 f (z)dz 0, AEBBEAA
CF A A F
B
f (z)dz 0.
D1 E C1 B
AAF BBFA
︵︵
D
︵
E
︵
︵ ︵ AEBBEAA AEB BB BEA AA,
︵
︵
AAFBBFA AA AFB BB BFA,
22
2 不定积分 f z 的原函数的一般表达式 F z C（其中C为 任意常数），称为 f z 的不定积分，即
f zdz Fz c （其中C为任意常数）
例如 sinzdz cos z c 其中c为任意常数
（换元积分法 分部积分法）
例 z sinzdz z d cos z z cos z cos zdz
二、复合闭路定理
设 f z在多连通域D内解析，C是D内的一条简单闭曲线，
C1, C2 , , Cn是在C内部的简单闭曲线，它们互不包含也互
不相交，且以C, C1, C2 , , Cn 为边界的区域全包含于D，
则
n
⑴
f zdz
C
k 1 Ck
f zdz
C1
n
⑵ f zdz f zdz 0
设f z在单连通域B内解析，则F z在B内是一解析函数，
且Fz f z, 即F z为f z的原函数. 证明
24
定理三
设f z在单连通域B内解析，Gz为f z的一个原函数，
则
z1 z0
f
zdz
Gz1 Gz0 .
解析函数的积分计算公式
证
z z0
f zdz,Gz均为f

《复变函数》(西安交大 第四版第六讲名师教学资料

《复变函数》(西安交大 第四版第六讲名师教学资料
n
an

a,
lim
n
bn

b.
“”
已
知 lim n
an
0, N 0,
n
a,
lim
n
bn

N ,恒有
b an
即，
a


2
，bn

b


2
又n (an a) i(bn b)
an a bn b
故
lim
n
2
2
其中c 为任意实的常数
又解 v 2x y v 2xy y2 ( x)
y
2
v u
v 2 y '( x)
x y
2y x
偏
x
积
'(x) x
(x) x2 c
2
分
法
y2 x2 v( x, y) 2xy c
2u 2u x2 y2 0,
同理有
2v x 2

2v y 2

0
即u及v 在D内满足拉普拉斯(Laplace)方程:
u 0,
v 0
其中

2 x 2

2 y 2
u u(x, y)，v v(x, y)是D内的调和函数。
定义 设u( x, y)为D内的调和函数, 称使得u iv 在D内构成解析函数的调和函数v( x, y)为u( x, y) 的 共 轭 调 和 函 数.
2 2
x2 y2 0
即（ 0)
则称 ( x, y)为D内的调和函数.
定理 若f (z) u( x, y) iv( x, y)在区域D内解析 u u( x, y)，v v( x, y)是D内的调和函数。

复变函数(西交大)第三讲共48页PPT资料

复变函数(西交大)第三讲共48页PPT资料

| x| 1 , z
| y z| 1 x z(1 i3 ) 0
f(z) lim f(z z)f(z) u i v
ቤተ መጻሕፍቲ ባይዱ 0
z
x x
定理2 函数f (z)=u(x, y)+iv(x, y)在D内解析充要 条件是 u(x, y) 和 v(x, y)在D内可微，且 满足Cauchy-Riemann方程
f'(z)lim f(zz)f(z)
z 0
z
设 ( z)f(z z)f(z)f'(z)
z
则 f (z+ Δz)-f(z)=f (z)Δz+(Δz)Δz (1), 且
lim(z)0
z0
令：f (z+Δz) f (z)=Δu+iΔv，f (z)= a+ib， (Δz)=1+i2 故（1）式可写为
Δu+iΔv = (a+ib)(Δx+iΔy)+(1+i2)(Δx+iΔy) =(aΔx-bΔy+1Δx2Δy)
f(z)limf(zz)f(z)
z0
z
[u(xx, y)i v(xx, y)][u(x, y)i v(x, y)]
lim
x0
x
u(xx, y)u(x, y)
v(xx, y)v(x, y)
lim
i lim
x0
x
x0
x
u i v x x
若沿平行于虚轴 z的 z 方z(式 x0)
f(z)limf(zz) f(z)
§2.2 解析函数的充要条件
1. 解析函数的充要条件 2. 举例
如果复变函数 w = f (z) = u(x, y) + iv(x, y)在定 义域 D内处处可导，则函数 w = f (z) 在 D内解析。

《复变函数》(西安交大 第四版)第七讲共48页

《复变函数》(西安交大 第四版)第七讲共48页
收敛圆周上.
2. 展开式的唯一性
利用泰勒级数可把解析函数展开成幂级数，这样 的展开式是否唯一？
结论 解析函数展开成幂级数是唯一的，就是它 的Taylor级数。
事实上，设f (z)用另外的方法展开为幂级数:
f ( z ) a 0 a 1 ( z z 0 ) a 2 ( z z 0 ) 2 a n ( z z 0 ) n
分析：
cn
1 n!
f
(n)(z0)
21ikf(z0)n1d
z0
k:z0 rR 代入(1)得
D
k
cn(z
n0
z0)nn0f(nn)(!z0)(zz0)n
n 021 ik( f(z0))n1d(zz0)n
21 ikn 0( f(z0))n1(zz0)nd 1)
D
z0
z
k
又 f(z)21 ikf( z)d 2)
比 1 )2 较 ) ,有 f( z ) ， n 0 ( f( z 0 ) )n 1 (z z 0 )n ( )
z z0 q 1,
z0
D
z0
z
k
注意 1 到 zz0 1(zz0)
1 z0
1
1 z z0
,
z0
1 z 1 z 0 1 z z z 0 0 (z z z 0 0 )2 (z z z 0 0 )n (2 )
当z0 0时,Tay级 lor数为：
f(z)f(0 )f'(0 )zf''(0 )z2 f(n )(0 )zn
2 !
n !
函数展开成Taylor级数的方法：
• 代公式 ---直接法 • 由展开式的唯一性，运用级数的代数运算、分
析运算和 已知函数的展开式来展开 ---间接法

西安交通大学复变函数试卷及参考答案

西安交通大学复变函数试卷及参考答案
1【B】；2【D】；3【C】；4【B】；5【C】
三证明：因为 ，由连续性的概念，取 >0，存在 ，
使当 时，有：
从而 即： 即： .
四解： 的参数方程为 ， ，
五求 在圆环域 和 内的罗朗展开式。
六解：由于奇偶性， = ＝ .
七证明：由题意得，
欲证 ，只需要证明：
由于 ，故
又 =
代入前面 ，可得： =
二．选择题（每题4分，共20分）
1 是函数 的【】
A一级极点B本性奇点C可去奇点D零点
2函数 （ ； 为复常数）的解析区域是：【】
A复平面B扩充复平面
C除去原点的复平面D除去原点与负实轴的复平面
3设 为正向圆周 ，则积分 的值为【】
A4B C0D
4函数 在复平面上的所有有限奇点处留数的和：【】
A4B1C－1D2
5分式线性映射 将上半平面 映为上半平面 ， , ,则映射 可能为：【】
A ,B ,C ,D
三设函数 在 连续，且 ，求证:可以找到 的一个邻域，使函数 在此邻域的内取值不为零。
四计算积分 ，其中 是从点A(1,0)到B(-1,0)的上半个圆周。
五求 在圆环域 和 内的罗朗展开式。
六计算 , 。
七设 在 上解析，且为分式线性映射， ， 将 映为 ，证明：
故不等式得证。
又因为 ，则：
共2页第2页
课程复变函数答案
二.填空（每题4分，共40分）
1． 的指数形式：
2
3
4函数 解析，则则
5
6
7函数 的奇点： ，二级极点； 为一级极点（说出类型，如果是极点，则要说明阶数）
8将函数 展开为 的幂函数：
9设 的正向，求积分 1/2

西安交通大学复数与复变函数教学PPT

西安交通大学复数与复变函数教学PPT
a 2 b2 1 ab x x 2 1
解得 a x, 所以
b x2 1
1 2ix x 2 1 ( x i x 2 1)
西安交通大学
例3.证明 | z1 z2 |2 | z1 z2 |2 2(| z1 |2 | z2 |2 ), 并说明几何意义 证：| z1 z2 |2 ( z1 z2 )( z1 z2 )
y Im( z )
所以，2）的方程为
Im( z ) 5
z z 10i 0
zz zz ,y 方程较复杂时，一般用： x 2 2i
西安交通大学
例6 说明下列方程所表示的平面图形.
1. z 2i z 2 2. z 1, Im z 0
解：
1. z 2i z 2
再将模变到原来的r2倍
y
r1r2
z1 z2
r2
2
z2 1 2
r1 z1
1 2
o
1
x
西安交通大学
类似得
z1 r1 i (1 2 ) e . z2 r2
从而
两个复数商的模等于它们模的商； 两个复数商的辐角等于它们辐角的差.
西安交通大学
2）复数的乘幂与方根 n次幂
z r e z .z ...z
西安交通大学
例1.计算 3 8 ，并说明几何意义。 解：3 8 3 8e i 2e
k 0,1,2 2k 2k 2 cos( ) i sin( ) , k 0,1,2 3 3 1 i 3 k0 y 2 k 1 w1 k2 1 i 3 ,
18世纪： 1. 欧拉（L.Euler）建立复数理论，

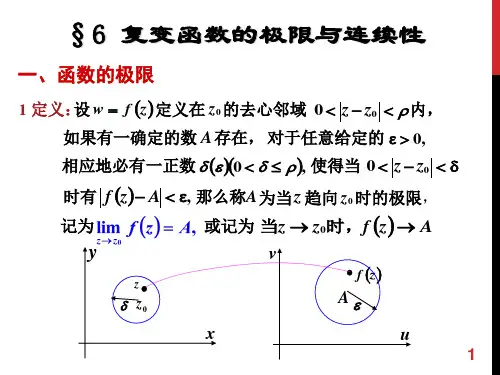
西安交大工程数学复变函数第四版1.6

西安交大工程数学复变函数第四版1.6
x2 y2
ux, y x , vx, y 0.
x2 y2
让z沿直线y kx趋于零，则有
lim u x, y lim x lim
x
x0
ykx
x0
ykx
x2 y2
x0
ykx
1 k2 x2
1
1 k2
lim ux, y不存在，lim f z不存在.
x0
z0
y0
[证法2]令z rcos i sin , 则f z r cos cos .
ux, y, vx, y在x0 , y0 处连续
定理四
1 f z, gz在z0处连续
f
z
g z ,
f
zgz,
f g
z z
g
z0
0在z0处连续.
2 h gz在z0处连续, w f h在h gz0 处连续
w f gz在z0处连续.
4
3 结论：
① 有理整函数(多项式) w Pz a0 a1z a2z2 anzn
对复平面内所有的z都是连续的.
②
有理分式函数
w
Pz Qz
[P(z),Q(z)为多项式]
对复平面内使分母不为零的点都是连续的.
③
函数
f
(z)
在曲线C上
z
0点处连续是指
lim
z z0
f (z)
f (z0 ) ,
zC
在闭曲线或包括曲线端点在内的曲线段上连续的函数f(z) ,
在曲线上是有界的，即 M 0, 使得当 z C 时，恒有
f z M.
5
课后习题：
7
x x0
x x0
y y0
y y0
定理二 lim f z A, lim gz B,

复变函数西安交大 第四版第三讲PPT课件

复变函数西安交大 第四版第三讲PPT课件

第18页/共46页
§2.3 初等函数
1. 指数函数 2. 三角函数和双曲函数 3. 对数函数 4. 乘幂与幂函数 5. 反三角函数与反双曲函数
第21页/共46页
内容简介
本节将实变函数的一些常用的初等 函数推广到复变函数情形，研究这些初等 函数的性质，并说明它的解析性。
第22页/共46页
u 2x u 2 y v 0 v 0
x
y
x
y
仅在点z = 0处满足C-R条件，故
w z 2 仅在z 0处可导，但处处不解析。
第16页/共46页
例2 求证函数
w
u( x, y) iv( x,
y)
x2
x
y2
i
x2
y
y2
1 z
在z x iy 0处 解 析 ， 并 求dw . dz
e zi e zi cosz
(3)
2i
2
称 为z的 正 弦 与 余 弦 函 数
第27页/共46页
正弦与余弦函数的性质
1)sinz及cosz是T 2 周期函数
[cos(z 2 ) ei(z2 ) ei(z2 )
eize2i eize2i
2
2
eiz eiz
cos z]
sin( z 2 ) sin z
u v v u x y x y
由此可以看出可导函数的实部与虚部有密切 的联系.当一个函数可导时,仅由其实部或虚部就可 以求出导数来.
利用该定理可以判断那些函数是不可导的.
第12页/共46页
使用时: i) 判别 u(x, y)，v (x, y) 偏导数的连续性，
(因为u(x,y),v(x,y)具有一阶连续偏导数可推出它们可 微)

《复变函数》第一讲

《复变函数》第一讲
1. 复数的乘积与商 复数的乘积与商 2. 复数的乘幂 复数的乘幂 3.复数的 3.复数的方根 复数的方根
1. 乘积与商
定理1 定理 两个复数乘积的模等于它们的模相乘， 两个复数乘积的模等于它们的模相乘， 两个复数乘积的辐角等于它们的辐角相加。 两个复数乘积的辐角等于它们的辐角相加。 z1=r1(cosθ1+isinθ1)=r1eiθ1 z2=r2(cosθ2+isinθ2)=r2eiθ2 则 z1z2=r1r2(cosθ1+isinθ1)( cosθ2+isinθ2) = r1r2[cos (θ1+θ2)+isin(θ1+θ2)] =r1r2e i(θ1+θ2) 因此 |z1z2|=r1r2，Arg(z1z2)=Argz1+Argz2
课程简介
课程名称 复变函数 教 材 《复变函数》(四版) 复变函数》
西安交通大学高等数学教研室 编
总 学 时 教师姓名
54学时
__张广亮 张广亮__ 张广亮
对
复变函数（自变量为复数的函数） 象 复变函数（自变量为复数的函数）
研究复变数之间的相互依赖关系， 主要任务 研究复变数之间的相互依赖关系， 具体地就是复数域上的微积分。 具体地就是复数域上的微积分。 复数与复变函数、解析函数、 主要内容 复数与复变函数、解析函数、 复变函数的积分、级数、留数、 复变函数的积分、级数、留数、 共形映射等。 共形映射等。
3.共轭复数 共轭复数
的共轭复数. 定义 若z=x+iy , 称z=x-iy 为z 的共轭复数 •共轭复数的性质
(1) ( z1 ± z 2 ) = z1 ± z 2
( z1 z 2 ) = z1 z 2
(conjugate)

西安交大西工大 考研备考期末复习 工程数学复变函数 复数与复变函数概念

西安交大西工大 考研备考期末复习 工程数学复变函数 复数与复变函数概念

3
u
x2 y2 4
z1 i
y
z2 1 2i
z3 1
z1 z2 z3 O
Im z y 0 Re z x 0 z 1
v
Im w 2xy 0
w2
w u2 v2 1
O
x
w1 w3
u
w1 1 w2 3 4i w3 1
复变函数
函数 w=z2 对应于两个二元实变函数: u=x2y2, v=2xy
x x(t)
y y(t) ( t )
所决定的点集C，称为z平面上的一条连续曲线。
令z x(t) iy(t)
( t )
z z(t)
参数表达式 复数表达式
复变函数
2.光滑曲线 设曲线C的参数方程为: z x(t) iy(t)
( t )
又在α≤t≤β上，x’(t)和y’(t)连续且
当反函数单值时z [ f (z)] z G (一般z [ f (z)])
复变函数
当函数(映射)w f (z)和其反函数(逆映射)
z (w)都是单值的，则称函数(映射)w f (z)
是 一 一 的 。 也 称 集 合G与 集 合G 是 一 一 对 应 的 。
例4 已知映射 w 1 ,判断 : z平面上的曲线 x2 y2 1被
三.用复数表达式表示常见区域
1.单位圆内部 z 1
复变函数
2.圆环域
r1 z z0 r2其中r1，r2都是大于0的实数
3.带状区域
x1 Rez x2
y1
Imz
y2
4.角形域 1 arg z 2
5.上半平面 Imz 0
6.左半平面 Rez 0
§5 复变函数
复变函数
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第四章
!
级!数
内容提要
一 !复 数 项 级 数
!
!!复 数 列 的 极 限
复数列极限与 实 数 列 极 限 的 定 义 形 式 上 相 同!复 数 列 ""##"
"!# #$"##$#"!!$!% % &收 敛 于 复 数""!#$" 的 充 要 条 件 为
%&’!# "!!! !%&’"# "")
(
# 称 / 为幂级数 (# 的收 敛 半 径!.(.% / 为 收 敛 圆)在 #%* (
# !" 两种情形中!我们也称 (# 的收敛半径为*和 () #%* (
# 综上!我们有*幂级数 +#(# 在收敛圆.(.%/ 内不仅收 #%*
敛而且绝对收敛!在收敛圆外发 散!在 收 敛 圆 .(.% / 上
#" (
(* 收敛)*$(*&称为它的和)如果级数在 ) 内处处收 敛!那 么 它 的和一定是( 的一个函数*$(&
*$(&"’!$(&#’$$(&# % #’#$(&# %
(
# -$(&称为级数 ’#$(&的和函数)当 #%! ’#$(&"+#.!$(."&#.!
或
时 !函 数 项 级 数 为
’#$(&"+#.!(#.!
#" (
#" (
因此!复数列极限的性 质 也 与 实 数 列 极 限 的 性 质 相 似!并 且 可
将复数列极限的计算问题转化为实数列极限的计算问题)
$)复 数 项 级 数
$!&复 数 项 级 数 敛 散 性 与 和 的 定 义 形 式 上 也 与 实 数 项 级 数 的 相
应概念相同)
(
# $$&复数项级数 !#$!# % "# #$&#&收 敛 的 充 要 条 件 是 级 数 #%!
对所有的(!和函数存在&!其次证明对所有的(!和函数 7$(&
满足所给的方程)而这一点 只 需 要 利 用 幂 级 数 的 逐 项 求 导 性
!#
" !#
$.$&$#-! #
" !.
$.!&#$ #
(
(
(
(
# # # # 级数 "# #%!
"
#%!
! #
发散!级数 &#
#%!
"
#%!
$.!&#
! #
收敛!
故原级数必发散)
$+&由于很难分离出!#"#H#$$!#$&&# 的 实 部 与 虚 部!故 采
$ & 用绝对收敛准则)易见(!#("#$
!
#
!且
!H
%&’
#
!(!#("%&’
!##$
(
!
"
!
&!
#" (
#" (
!H !H
根据正项 级 数 的 根 值 法!故 知 原 级 数 收 敛!而 且 绝 对 收
敛)
$@&由 于(!#("
$!#$&#
#
$$:CD$#
"$#$0$#:0$;#"3##$3.#
$ &3#
!而
级
数##("!3$# 是一收敛的等比级数!根据正项级数的 比 较 准 则!
+如!.!(!3(!D&?(!:CD(!%?$!#(&!$!#(&!$! 为 复 数&等 函 数 的 (#"% (
第四章!级!数
幂 级 数 展 开 式 ,!通 过 对 幂 级 数 进 行 变 量 代 换 !四 则 运 算 和 分 析 运 算 $逐 项 求 导 !逐 项 积 分 等 &!求 出 所 给 函 数 的 幂 级 数 展 开 式 )
&
& 为圆环内绕! 的任何一条正向简单闭曲线!并且展开式是惟
一的!
+!函 数 展 开 成 洛 朗 级 数 的 方 法
洛 朗 级 数 是 泰 勒 级 数 的 推 广 !圆 环 内 解 析 函 数 展 开 成 洛 朗 级 数 的一般方法并不 是 按 照 上 面 公 式 计 算 洛 朗 系 数+# 进 行!而 主 要 是 根 据 洛 朗 级 数 展 开 式 的 惟 一 性 !利 用 已 知 的 幂 级 数 展 开 式 去求所需要的洛朗展开式!
#%*
(
(
(
$# &$# & # "#(#
&#(# " $"#&*-"#,!&!- % -"*&#&(#$乘
#%*
#%*
#%*
积运算&
$$&复 合 运 算 性 质
(
# 设 当.$.&0时!’$$&" "#$#!当,(,&/ 时!$"A$(& #%*
解 析 且 ,A$(&,& 0!则 当 .(.& / 时!’+1$(&,"
敛散性)
二 !幂 级 数
!)函 数 项 级 数 与 幂 级 数
设"’#$(&#为定义在区域 ) 内的复函数列 表达式
(
#’#$(&"’!$(&#’$$(&# % #’#$(&# %
#%!
称为复变函数项级数!
*#$(&"’!$(&#’$$(&# %’#$(& 称为级数部分和) 若(*$)!极 限%&’*#$(*&"*$(*&存 在!则 称 函 数 项 级 数 在 点
典型例题与解题技巧
$例!%!考察下列级数是否收敛. 是否绝对收敛.
(#"& (
!! 复变函数同步辅导及习题全解
#$ & # (
$!&
#%!
!.#!$
3$%#
’! !
(
$$&
#%!
!-
$,$&$#-! ’ #
#(
$+&
#%!
#$ H$
$!-$$&#’
#(
$@&
$!-$&#
#
!
#%! $$:CD$#
解 题 分 析 ! 此 题 考 察 级 数 收 敛 /发 散 /绝 对 收 敛 的 判 别 方 法 !
和性质 )
$)洛 朗 展 开 定 理
在圆环0&((.!(&/$0**!/+ # (&内 解 析 的 函 数 ’$(&必 可 展 开 成 如 下 的 双 边 幂 级 数 $称 为 洛 朗 级 数 &
其中
(
# ’$(&" +#$(,!&# #%,(
, +#

%
! $%$
$(’,$(!& &#-!>($# %*!3!!3$!%&
(#"# (
!! 复变函数同步辅导及习题全解
(
#+#$(,"&# "+* -+!$(,"&-+$$(,"&$ - %
#%*
! -+#$(,"&# - %
或
(
#+#(# "+* -+!(-+$($ - % -+#(# - %
#%*
这种级数称为幂级数!其中" 为定复数)
(
(
# # $!&若 +#(# 在(* %*点收敛!则 +#(# 在.(.&.(*.内绝
# ’$(&%
( #%*
’$##&-$!&$(,!&#
而且展开式是惟一的)
应该指出!如果’$(&在点! 解析!那么使’$(&在! 的泰勒展开
式成立的圆域半径等 于 点! 到’$(&的 奇 点 之 间 的 最 短 距 离)
此外幂级数 的 和 函 数 在 收 敛 圆 周 上 至 少 有 一 个 奇 点)函 数 ’
(
(
# # (* 点 4#(# 绝对收敛!即级数 ,4#,(,(*,# 收敛)
#%!
#%!
由于,(,& /!所以,(0(*,&!)于是有
(
(
# # ,4#(#," ,4#,(,(#,
#%!
#%!
(
# " ,4#,(,(*.#(,(0(*,# #%!
(
# + ,4#,(,(*.# #%!
(
(
# # 由于 ,4#,(,(*.# 收敛!所以 .4#(#.收敛)故得级数
$(&在点! 解析等价 于’$(&在! 的 邻 域 内 可 以 展 开 成 幂 级 数
#(
#%*
’$##&-$!&$(,!&#!
$)函 数 展 开 成 泰 勒 级 数 的 方 法
直 接 法 $直 接 用 泰 勒 定 理 &与 间 接 法 )所 谓 间 接 法 就 是 根 据 函 数 的 幂 级 数 展 开 式 的 惟 一 性 !利 用 一 些 已 知 函 数 的 幂 级 数 展 开 式