(完整版)数字信号处理课后答案_史林版_科学出版社
- 格式:doc
- 大小:2.17 MB
- 文档页数:30

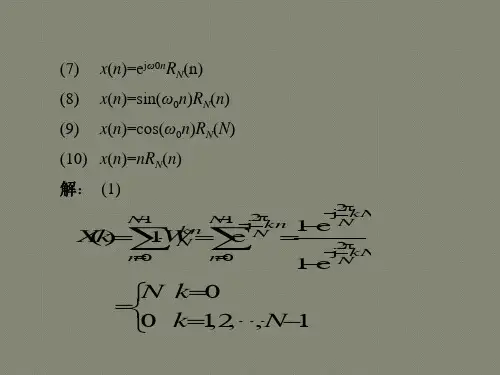



==============================绪论==============================1。
A/D 8bit 5V 00000000 0V 00000001 20mV 00000010 40mV 00011101 29mV==================第一章 时域离散时间信号与系统==================1。
①写出图示序列的表达式答:3)1.5δ(n 2)2δ(n 1)δ(n 2δ(n)1)δ(n x(n)-+---+++= ②用(n ) 表示y (n )={2,7,19,28,29,15}2. ①求下列周期)54sin()8sin()4()51cos()3()54sin()2()8sin()1(n n n n n ππππ-②判断下面的序列是否是周期的; 若是周期的, 确定其周期。
(1)A是常数 8ππn 73Acos x(n)⎪⎪⎭⎫ ⎝⎛-= (2))81(j e )(π-=n n x 解: (1) 因为ω=73π, 所以314π2=ω, 这是有理数, 因此是周期序列, 周期T =14。
(2) 因为ω=81, 所以ωπ2=16π, 这是无理数, 因此是非周期序列。
③序列)Acos(nw x(n)0ϕ+=是周期序列的条件是是有理数2π/w 0。
3.加法 乘法序列{2,3,2,1}与序列{2,3,5,2,1}相加为__{4,6,7,3,1}__,相乘为___{4,9,10,2} 。
移位翻转:①已知x(n)波形,画出x(—n )的波形图。
②尺度变换:已知x(n)波形,画出x (2n )及x(n/2)波形图.卷积和:①h(n)*求x(n),其他2n 0n 3,h(n)其他3n 0n/2设x(n) 例、⎩⎨⎧≤≤-=⎩⎨⎧≤≤=}23,4,7,4,23{0,h(n)*答案:x(n)=②已知x (n )={1,2,4,3},h (n )={2,3,5}, 求y (n )=x (n )*h (n )x (m )={1,2,4,3},h (m )={2,3,5},则h (—m )={5,3,2}(Step1:翻转)解得y (n )={2,7,19,28,29,15}③(n)x *(n)x 3),求x(n)u(n u(n)x 2),2δ(n 1)3δ(n δ(n)2、已知x 2121=--=-+-+=}{1,4,6,5,2答案:x(n)=4. 如果输入信号为,求下述系统的输出信号。





数字信号处理习题及答案HEN system office room 【HEN16H-HENS2AHENS8Q8-HENH1688】==============================绪论============================== 1. A/D 8bit 5V 00000000 0V 00000001 20mV 00000010 40mV 00011101 29mV==================第一章 时域离散时间信号与系统================== 1.①写出图示序列的表达式答:3)1.5δ(n 2)2δ(n 1)δ(n 2δ(n)1)δ(n x(n)-+---+++= ②用(n) 表示y (n )={2,7,19,28,29,15} 2. ①求下列周期②判断下面的序列是否是周期的; 若是周期的, 确定其周期。
(1)A是常数 8ππn 73Acos x(n)⎪⎪⎭⎫ ⎝⎛-= (2))81(j e )(π-=n n x 解: (1) 因为ω=73π, 所以314π2=ω, 这是有理数, 因此是周期序列, 周期T =14。
(2) 因为ω=81, 所以ωπ2=16π, 这是无理数, 因此是非周期序列。
③序列)Acos(nw x(n)0ϕ+=是周期序列的条件是是有理数2π/w 0。
3.加法乘法序列{2,3,2,1}与序列{2,3,5,2,1}相加为__{4,6,7,3,1}__,相乘为___{4,9,10,2} 。
移位翻转:①已知x(n)波形,画出x(-n)的波形图。
②尺度变换:已知x(n)波形,画出x(2n)及x(n/2)波形图。
卷积和:①h(n)*求x(n),其他2n 0n 3,h(n)其他3n 0n/2设x(n) 例、⎩⎨⎧≤≤-=⎩⎨⎧≤≤=②已知x (n )={1,2,4,3},h (n )={2,3,5}, 求y (n )=x (n )*h (n )x (m )={1,2,4,3},h (m )={2,3,5},则h (-m )={5,3,2}(Step1:翻转)解得y (n )={2,7,19,28,29,15} ③(n)x *(n)x 3),求x(n)u(n u(n)x 2),2δ(n 1)3δ(n δ(n)2、已知x 2121=--=-+-+=4. 如果输入信号为,求下述系统的输出信号。
第一章 作业题 答案############################################################################### 1.2一个采样周期为T 的采样器,开关导通时间为()0T ττ<<,若采样器的输入信号为()a x t ,求采样器的输出信号()()()a a x t x t p t ∧=的频谱结构。
式中()()01,()0,n p t r t n t r t ττ∞=-∞=-≤≤⎧=⎨⎩∑其他解:实际的采样脉冲信号为:()()n p t r t n τ∞=-∞=-∑其傅里叶级数表达式为:()000()jk tn p t Sa k T eTωωτω∞=-∞=∑采样后的信号可以表示为:()()()ˆa a xt x t p t δ= 因此,对采样后的信号频谱有如下推导:()()()()()()()()()()()()()0000000000000ˆˆsin 1j t a a jk t j t a n jk t j t a k j k ta k ak a k X j x t e dtx t Sa k T e e dtTSa k T x t e e dtTSa k T x t edtTSa k T X j jk Tk T X j jk T kωωωωωωωωτωωτωωτωωτωωωωωω∞--∞∞∞--∞=-∞∞∞--∞=-∞∞∞---∞=-∞∞=-∞∞=-∞Ω=====-=-⎰∑⎰∑⎰∑⎰∑∑%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% 1.5有一个理想采样系统,对连续时间信号()a x t 进行等间隔T 采样,采样频率8s πΩ=rad/s ,采样后所得采样信号()a x t ∧经理想低通滤波器()G j Ω进行恢复,已知()41/4,,4G j ππ⎧Ω≤⎪Ω=⎨Ω>⎪⎩今有两个输入信号12()cos(2)()cos(5)a a x t t x t t ππ==和,对应的输出信号分别为12()()a a y t y t 和,如题1.5图所示,问12()()a a y t y t 、有没有失真,为什么?题1.5图 理想采样系统与恢复理想低通滤波器解:因为是理想采样系统,因此采样后的信号频谱可以表示为:()()1ˆa a s k X j X j jk T ∞=-∞Ω=Ω-Ω∑8s πΩ=,12πΩ=,25πΩ=,折叠频率为2s Ω,而滤波器对4πΩ≤的信号通过,因此有如下图:结论:1)1()a y t 不失真、2()a y t 失真。
2)输出信号中存在两种频率:2π、3π%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% 1.6已知连续时间信号()a x t 是频率为300Hz 、400Hz 、1.3KHz 和4.3KHz 的正弦信号的线性组合。
现以2KHz 的采样频率对()a x t 进行采样。
若恢复滤波器是一截止频率为900Hz 的理想低通滤波器,试确定通过恢复滤波器后的输出信号()a y t 中的各频率分量。
解:因为是理想采样系统,因此采样后的信号频谱可以表示为:()()1ˆa a s k X j X j jk T ∞=-∞Ω=Ω-Ω∑滤波后信号中的频率分量为:300Hz 、400Hz 、700Hz 。
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%1.7已知一模拟恢复信号()a x t 的频谱如题1.7图所示。
对其等间隔T 采样所得离散时间信号(序列)为()()a x n x nT =。
(1)当采样间隔()0/3T π=Ω时,画出序列()x n 的频谱图形。
(2)试确定采样信号频谱不混叠的最低采样频率,并画出此时()x n 的频谱图形。
(3)画出由(3)中的序列()x n 恢复()a x t 的框图(可用复理想低通滤波器)。
1Ω题1.7图()a x t 的频谱图形解:采样间隔为()0/3T π=Ω,因此采样频率为026Tπ=Ω。
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%第二章 作业题 答案%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%2.1将序列1,01,1()0,22,30,n n x n n n =⎧⎪-=⎪⎪==⎨⎪=⎪⎪⎩其他表示为()u n 及()u n 延迟的和。
解:首先将()x n 表示为单位脉冲序列的形式:()()()()=123x n n n n δδδ--+-对于单位脉冲函数()n δ,用单位阶跃序列()u n 表示,可得:()()()1n u n u n δ=--将上式带入到()x n 的单位脉冲序列表达式中,可得:()()()()()()()()()()()()()()()1231122342122324x n n n n u n u n u n u n u n u n u n u n u n u n u n δδδ=--+-=------+---⎡⎤⎡⎤⎣⎦⎣⎦=--+-+--- %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%2.5判断下列序列中,哪一个是周期序列,如果是周期序列,求出它的周期。
(1)()sin1.2x n n = (2)()sin9.7x n n π= (5)()sin()cos()47nnx n ππ=-解:理论分析详见P18性质7)周期序列题中设计到的是正弦信号,对于正弦信号()0()sin x n A n ωϕ=+,分析其周期性,则需判断:02πω1)为整数,则周期;2)为有理数,则周期;3)为无理数则非周期。
观察(1)、(2)、(5),0ω依次为:0 1.2ω=、09.7ωπ=、12,47ππωω==,从而可知(1)为非周期,(2)、(5)为周期序列。
(2)中,022209.797ππωπ==,因此周期20N =。
(5)中,第一部分周期为1028N πω==,第二部分周期为20214N πω==,因此序列周期为56N =。
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%2.9试确定下列系统是否为线性时不变系统?(1) ()()()sin y n x n n ω=。
(2) ()()0nm y n x m ==∑, m 为正整数。
解:利用线性时不变系统定义、性质分析。
(1)()()()sin y n x n n ω= 线性分析:()()()()()()()()()()()()12121212sin sin sin y n T ax n bx n ax n bx n n ax n n bx n n aT x n bT x n ωωω'=+⎡⎤⎣⎦=+⎡⎤⎣⎦=+=+⎡⎤⎡⎤⎣⎦⎣⎦因此为线性系统。
时不变分析:()()()000sin y n n x n n n n ω-=--⎡⎤⎣⎦而系统输入为()0x n n -时,()()()()00sin y n T x n n x n n n ω'=-=-⎡⎤⎣⎦得:()()0y n y n n '≠-,因此为时变系统。
综上,()()()sin y n x n n ω=为线性时变系统。
(2)()()0nm y n x m ==∑线性分析:()()()()()()()()()1212012012nm n nm m y n T ax n bx n ax m bx m ax m bx m aT x m bT x m ==='=+⎡⎤⎣⎦=+⎡⎤⎣⎦=+=+⎡⎤⎡⎤⎣⎦⎣⎦∑∑∑因此为线性系统。
时不变分析:()()()()()()()()()()()0000001012+01+n n m y n n x m x x x x x x x x x n n -=-==++++++++-⎡⎤⎡⎤⎡⎤⎣⎦⎣⎦⎣⎦∑……而系统输入为()0x n n -时,()()()()()()()()()000000000=++1++1nm y n T x n n x m n x n x n x n x n x n x n n ='=-=-⎡⎤⎣⎦-----++-⎡⎤⎡⎤⎣⎦⎣⎦∑...+...得:()()0y n y n n '≠-,因此为时变系统。
综上,()()0nm y n x m ==∑为线性时变系统。
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% 2.11试求题2.11图所示线性时不变系统的单位脉冲响应()h n ,图中[]1()40.5()(3)n h n u n u n =⨯--23()()(1)()h n h n n u n ==+4()(1)h n n δ=- 5()()4(3)h n n n δδ=--题2.11图 线性时不变系统如果输入序列()()(1)x n n n δδ=--,求该系统的输出序列()y n 。
解:此题涉及到了线性时不变系统的输入、输出关系,即:()()()*y n x n h n =以及线性卷积的性质:交换律、结合律、分配律。
系统的输入输出关系可表示为:()()()()()(){}()()12345****y n x n h n h n h n h n x n h n =-+⎡⎤⎣⎦将()()1,2,3,4,5i h n i =进行变形,尽量表示为单位脉冲序列的形式,以方便运算,则:()()()()()()()()()140.5340.5124212n n h n u n u n n n n n n n δδδδδδ=⨯--⎡⎤⎣⎦=⨯+-+-⎡⎤⎣⎦=+-+- ()()()()231h n h n n u n ==+ ()()41h n n δ=- ()()()543h n n n δδ=--此时注意:()()()()()()()()()()()()()()()()234*111111h n h n h n n u n n u n n n u n nu n nu n nu n u n n n u n δδ-=+-+-=+--=--+=+()()()()()()()()()()()()()()()1234**4212*42124212h n h n h n h n n n n n n u n n n n n n n u n u n u n δδδδδδδ-⎡⎤⎣⎦=+-+-+⎡⎤⎡⎤⎣⎦⎣⎦=+-+-++-+-()()()1x n n n δδ=--,与之卷积实质是序列本身与序列右移一个单位所得新序列的差。