下载文档原格式
Chapter 2 Solutions2.1 最小采样频率为两倍的信号最大频率，即44.1kHz 。
2.2 (a)、由ω = 2πf = 20 rad/sec ，信号的频率为f =3.18 Hz 。
信号的奈奎斯特采样频率为6.37 Hz 。
(b)、35000π=ω，所以f = 833.3 Hz ，奈奎斯特采样频率为1666.7 Hz 。
(c)、73000π=ω，所以f = 214.3 Hz ，奈奎斯特采样频率为428.6 Hz 。
2.3 (a) 12580001f 1T S S ===μs (b)、最大还原频率为采样频率的一半，即4000kHz 。
2.4 ω = 4000 rad/sec ，所以f = 4000/(2π) = 2000/π Hz ，周期T = π/2000 sec 。
因此，5个周期为5π/2000 = π/400 sec 。
对于这个信号，奈奎斯特采样频率为2(2000/π) = 4000/π Hz 。
所以采样频率为f S = 4(4000/π) = 16000/π Hz 。
因此5个周期收集的采样点为(16000/π samples/sec )(π/400 sec) = 40。
2.5 ω = 2500π rad/sec ，所以f = 2500π/(2π) = 1250 Hz ，T = 1/1250 sec 。
因此，5个周期为5/1250 sec 。
对于这个信号，奈奎斯特采样频率为2(1250) = 2500 Hz ，所以采样频率为f S = 7/8(2500) = 2187.5 Hz 。
采样点数为(2187.5 点/sec)(5/1250 sec) = 8.75。
这意味着在模拟信号的五个周期内只有8个点被采样。
事实上，对于这个信号来说，在整数的模拟周期中，是不可能采到整数个点的。
2.62.7 信号搬移发生在kf S ± f 处，换句话说，频谱搬移发生在每个采样频率的整数倍 (a) 采样频率满足奈奎斯特采样定理，所以没有混叠发生。
西安电子 ( 高西全丁美玉第三版 ) 数字信号处理课后答案1.2 教材第一章习题解答1. 用单位脉冲序列 (n) 及其加权和表示 题 1 图所示的序列。
解：x( n)(n4) 2 (n 2) ( n 1)2 (n)(n 1) 2 (n 2) 4 ( n 3)0.5(n 4)2 (n 6)2n 5, 4 n 12. 给定信号： x( n)6,0n 40, 其它（1）画出 x( n) 序列的波形，标上各序列的值； （2）试用延迟单位脉冲序列及其加权和表示 x(n) 序列；（3）令 x 1( n) 2x(n 2) ，试画出 x 1( n) 波形；（4）令 x 2 (n) 2x(n 2) ，试画出 x 2 (n) 波形；（5）令 x 3 (n) 2x(2 n) ，试画出 x 3 (n) 波形。
解：（ 1） x(n) 的波形如 题 2 解图（一） 所示。
（ 2）x(n)3 ( n 4)(n 3) (n 2) 3 ( n 1) 6 (n) 6 (n 1)6 ( n 2)6(n 3) 6 (n 4)（ 3） x 1 (n) 的波形是 x(n) 的波形右移 2 位，在乘以 2，画出图形如 题 2 解图（二） 所示。
（ 4） x 2 (n) 的波形是 x(n) 的波形左移 2 位，在乘以 2，画出图形如 题 2 解图（三） 所示。
（ 5）画 x 3 (n) 时，先画 x(-n) 的波形，然后再右移2 位， x3 ( n) 波形如 题 2 解图（四） 所示。
3. 判断下面的序列是否是周期的，若是周期的，确定其周期。
（1） x( n)Acos(3n) ，A 是常数；78（2）x(n)j ( 1n)e 8。
解：（1）w 3214T=14 ；7,，这是有理数，因此是周期序列，周期是w3（2）w 1 , 216 ，这是无理数，因此是非周期序列。
8w5. 设系统分别用下面的差分方程描述，x(n) 与 y(n) 分别表示系统输入和输出，判断系统是否是线性非时变的。
数字信号处理课后习题答案HEN system office room 【HEN16H-HENS2AHENS8Q8-HENH1688】数字信号处理（姚天任江太辉）第三版课后习题答案第二章判断下列序列是否是周期序列。
若是，请确定它的最小周期。
（1）x(n)=Acos(685ππ+n )（2）x(n)=)8(π-ne j（3）x(n)=Asin(343ππ+n )解 (1)对照正弦型序列的一般公式x(n)=Acos(ϕω+n )，得出=ω85π。
因此5162=ωπ是有理数，所以是周期序列。
最小周期等于N=)5(16516取k k =。
（2）对照复指数序列的一般公式x(n)=exp[ωσj +]n,得出81=ω。
因此πωπ162=是无理数，所以不是周期序列。
（3）对照正弦型序列的一般公式x(n)=Acos(ϕω+n )，又x(n)=Asin(343ππ+n )＝Acos(-2π343ππ-n )＝Acos(6143-n π)，得出=ω43π。
因此382=ωπ是有理数，所以是周期序列。
最小周期等于N=)3(838取k k =在图中，x(n)和h(n)分别是线性非移变系统的输入和单位取样响应。
计算并列的x(n)和h(n)的线性卷积以得到系统的输出y(n)，并画出y(n)的图形。
解 利用线性卷积公式y(n)=∑∞-∞=-k k n h k x )()(按照折叠、移位、相乘、相加、的作图方法，计算y(n)的每一个取样值。
(a) y(0)=x(O)h(0)=1y(l)=x(O)h(1)+x(1)h(O)=3y(n)=x(O)h(n)+x(1)h(n-1)+x(2)h(n-2)=4,n ≥2 (b) x(n)=2δ(n)-δ(n-1)h(n)=-δ(n)+2δ(n-1)+ δ(n-2)y(n)=-2δ(n)+5δ(n-1)= δ(n-3) (c) y(n)=∑∞-∞=--k kn k n u k u a)()(=∑∞-∞=-k kn a=aa n --+111u(n) 计算线性线性卷积 (1) y(n)=u(n)*u(n) (2) y(n)=λn u(n)*u(n)解：(1) y(n)=∑∞-∞=-k k n u k u )()(=∑∞=-0)()(k k n u k u =(n+1),n ≥0即y(n)=(n+1)u(n) (2) y(n)=∑∞-∞=-k k k n u k u )()(λ=∑∞=-0)()(k kk n u k u λ=λλ--+111n ,n ≥0即y(n)=λλ--+111n u(n)图所示的是单位取样响应分别为h 1(n)和h 2(n)的两个线性非移变系统的级联，已知x(n)=u(n), h 1(n)=δ(n)-δ(n-4), h 2(n)=a n u(n),|a|<1,求系统的输出y(n). 解 ω(n)=x(n)*h 1(n) =∑∞-∞=k k u )([δ(n-k)-δ(n-k-4)]=u(n)-u(n-4)y(n)=ω(n)*h 2(n) =∑∞-∞=k kk u a )([u(n-k)-u(n-k-4)]=∑∞-=3n k ka,n ≥3已知一个线性非移变系统的单位取样响应为h(n)=a n -u(-n),0<a<1 用直接计算线性卷积的方法，求系统的单位阶跃响应。
《数字信号处理》第三版课后习题答案数字信号处理课后答案1.2 教材第一章习题解答1. 用单位脉冲序列()n δ及其加权和表示题1图所示的序列。
解：()(4)2(2)(1)2()(1)2(2)4(3)0.5(4)2(6)x n n n n n n n n n n δδδδδδδδδ=+++-+++-+-+-+-+-2. 给定信号：25,41()6,040,n n x n n +-≤≤-??=≤≤其它（1）画出()x n 序列的波形，标上各序列的值；（2）试用延迟单位脉冲序列及其加权和表示()x n 序列；（3）令1()2(2)x n x n =-，试画出1()x n 波形；（4）令2()2(2)x n x n =+，试画出2()x n 波形；（5）令3()2(2)x n x n =-，试画出3()x n 波形。
解：（1）x(n)的波形如题2解图（一）所示。
（2）()3(4)(3)(2)3(1)6()6(1)6(2)6(3)6(4)x n n n n n n n n n n δδδδδδδδδ=-+-+++++++-+-+-+-（3）1()x n 的波形是x(n)的波形右移2位，在乘以2，画出图形如题2解图（二）所示。
（4）2()x n 的波形是x(n)的波形左移2位，在乘以2，画出图形如题2解图（三）所示。
（5）画3()x n 时，先画x(-n)的波形，然后再右移2位，3()x n 波形如题2解图（四）所示。
3. 判断下面的序列是否是周期的，若是周期的，确定其周期。
（1）3()cos()78x n A n ππ=-，A 是常数；（2）1()8()j n x n e π-=。
解：（1）3214,73w w ππ==，这是有理数，因此是周期序列，周期是T=14；（2）12,168w wππ==，这是无理数，因此是非周期序列。
5. 设系统分别用下面的差分方程描述，()x n 与()y n 分别表示系统输入和输出，判断系统是否是线性非时变的。
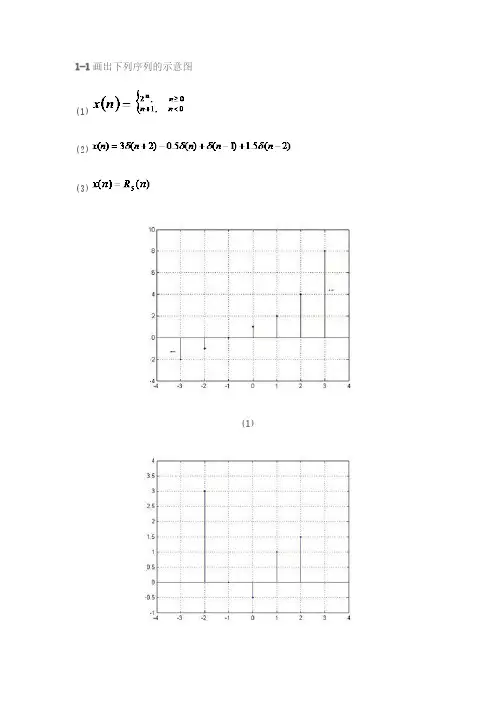
数字信号处理课后答案1.2 教材第一章习题解答1. 用单位脉冲序列()n δ及其加权和表示题1图所示的序列。
解：()(4)2(2)(1)2()(1)2(2)4(3) 0.5(4)2(6)x n n n n n n n n n n δδδδδδδδδ=+++-+++-+-+-+-+-2. 给定信号：25,41()6,040,n n x n n +-≤≤-⎧⎪=≤≤⎨⎪⎩其它（1）画出()x n 序列的波形，标上各序列的值；（2）试用延迟单位脉冲序列及其加权和表示()x n 序列； （3）令1()2(2)x n x n =-，试画出1()x n 波形； （4）令2()2(2)x n x n =+，试画出2()x n 波形； （5）令3()2(2)x n x n =-，试画出3()x n 波形。
解：（1）x(n)的波形如题2解图（一）所示。
（2）()3(4)(3)(2)3(1)6() 6(1)6(2)6(3)6(4)x n n n n n n n n n n δδδδδδδδδ=-+-+++++++-+-+-+-（3）1()x n 的波形是x(n)的波形右移2位，在乘以2，画出图形如题2解图（二）所示。
（4）2()x n 的波形是x(n)的波形左移2位，在乘以2，画出图形如题2解图（三）所示。
（5）画3()x n 时，先画x(-n)的波形，然后再右移2位，3()x n 波形如题2解图（四）所示。
3. 判断下面的序列是否是周期的，若是周期的，确定其周期。
（1）3()cos()78x n A n ππ=-，A 是常数；（2）1()8()j n x n e π-=。
解：（1）3214,73w w ππ==，这是有理数，因此是周期序列，周期是T=14； （2）12,168w wππ==，这是无理数，因此是非周期序列。
5. 设系统分别用下面的差分方程描述，()x n 与()y n 分别表示系统输入和输出，判断系统是否是线性非时变的。
数字信号处理课后答案1.2 教材第一章习题解答1. 用单位脉冲序列()n 及其加权和表示题1图所示的序列。
解：()(4)2(2)(1)2()(1)2(2)4(3)0.5(4)2(6)x n nn n n n nnn n 2. 给定信号：25,41()6,040,nnx n n其它（1）画出()x n 序列的波形，标上各序列的值；（2）试用延迟单位脉冲序列及其加权和表示()x n 序列；（3）令1()2(2)x n x n ，试画出1()x n 波形；（4）令2()2(2)x n x n ，试画出2()x n 波形；（5）令3()2(2)x n x n ，试画出3()x n 波形。
解：（1）x(n)的波形如题2解图（一）所示。
（2）()3(4)(3)(2)3(1)6()6(1)6(2)6(3)6(4)x n nnnn n n n n n （3）1()x n 的波形是x(n)的波形右移2位，在乘以2，画出图形如题2解图（二）所示。
（4）2()x n 的波形是x(n)的波形左移2位，在乘以2，画出图形如题2解图（三）所示。
（5）画3()x n 时，先画x(-n)的波形，然后再右移2位，3()x n 波形如题2解图（四）所示。
3. 判断下面的序列是否是周期的，若是周期的，确定其周期。
（1）3()cos()78x n A n，A 是常数；（2）1()8()j n x n e 。
解：（1）3214,73w w ，这是有理数，因此是周期序列，周期是T=14；（2）12,168ww，这是无理数，因此是非周期序列。
5. 设系统分别用下面的差分方程描述，()x n 与()y n 分别表示系统输入和输出，判断系统是否是线性非时变的。
（1）()()2(1)3(2)y n x n x n x n；（3）0()()y n x n n ，0n 为整常数；（5）2()()y n x n ；（7）0()()n m y n x m 。
Chapter 2 Solutions2.1 最小采样频率为两倍的信号最大频率，即44.1kHz 。
2.2 (a)、由ω = 2πf = 20 rad/sec ，信号的频率为f =3.18 Hz 。
信号的奈奎斯特采样频率为6.37 Hz 。
(b)、35000π=ω，所以f = 833.3 Hz ，奈奎斯特采样频率为1666.7 Hz 。
(c)、73000π=ω，所以f = 214.3 Hz ，奈奎斯特采样频率为428.6 Hz 。
2.3 (a) 12580001f 1T S S ===μs (b)、最大还原频率为采样频率的一半，即4000kHz 。
2.4 ω = 4000 rad/sec ，所以f = 4000/(2π) = 2000/π Hz ，周期T = π/2000 sec 。
因此，5个周期为5π/2000 = π/400 sec 。
对于这个信号，奈奎斯特采样频率为2(2000/π) = 4000/π Hz 。
所以采样频率为f S = 4(4000/π) = 16000/π Hz 。
因此5个周期收集的采样点为(16000/π samples/sec )(π/400 sec) = 40。
2.5 ω = 2500π rad/sec ，所以f = 2500π/(2π) = 1250 Hz ，T = 1/1250 sec 。
因此，5个周期为5/1250 sec 。
对于这个信号，奈奎斯特采样频率为2(1250) = 2500 Hz ，所以采样频率为f S = 7/8(2500) = 2187.5 Hz 。
采样点数为(2187.5 点/sec)(5/1250 sec) = 8.75。
这意味着在模拟信号的五个周期内只有8个点被采样。
事实上，对于这个信号来说，在整数的模拟周期中，是不可能采到整数个点的。
2.62.7 信号搬移发生在kf S ± f 处，换句话说，频谱搬移发生在每个采样频率的整数倍0 10 20 30 40 50 60 70 80 90 100 110 120 130 140 150 频率/kHz(b) 采样频率对于这个信号来说太低了，所以混叠发生了。
混叠图用虚线展示，最后的频谱用实线展示。
2.8 蜂窝电话信号是带宽受限的。
传输范围为30 kHz 。
最小采样频率至少为60kHz 。
在这道题中，60kHz 采样频率是足够的。
传输范围的基带搬移能被一个截止频率为2.9 (a)、信号在300Hz 处的镜像出现在3001000±-, 3000±, 3001000±,3002000± Hz ，......，即–1300, –700, 300, 700, 1300, 1700, 2300 Hz ，......。
这些信号只有一个位于奈奎斯特范围内（采样后能被恢复的范围，这道题为0到500Hz ）。
真实的信号频率为300Hz ，没有混叠发生。
(b)、信号的镜像出现在6001000±-, 6000±, 6001000±,6002000±Hz ，......，即–1600, –600, –400, 400, 600, 1400, 1600, 2600Hz ，......。
这些信号只有400Hz 落在奈奎斯特范围内。
这是混叠频率。
(c)、信号的镜像出现在13001000±-, 13000±, 13001000±,13002000±Hz ，......，即–2300, –1300, –300, 300, 700, 1300, 2300, 3300Hz ，......。
这些信号只有300Hz 落在奈奎斯特范围内。
这是混叠频率。
(b)、带宽受限信号在50到200Hz 发生混叠。
频谱倒置发生在基带。
0 30 60 90 1202.11 8kHz 的采样频率允许奈奎斯特范围为0到4kHz 。
在采样之后，信号的频谱搬移发生在–24000 ± 25000, –16000 ± 25000, –8000 ± 25000, 0 ± 25000, 8000 ± 25000, 16000 ± 25000Hz......。
奈奎斯特范围内唯一的镜像点为1000Hz 。
这就是混叠频率。
2.12 最简单的方法是通过看这两个信号有相同的采样点来比较两者。
采样时刻由nT S2.13 ± 0.2 MHz ，目标的实际频率为900.2MHz 。
2.14 车轮每转一圈，轮胎走过πd = .635π = 1.995 m 。
自行车速为15 km/h，即15000/3600 = 4.17 m/sec 。
因此，自行车每个轮子以cycles/sec 09.2m/cycle1.995m/sec17.4=的频率往复出现。
根据奈奎斯特采样定理，每个周期至少有两个采样点。
所以采样频率应为4.18 samples/sec 。
这能通过每100s 418次快照完成。
2.15 当信号以600Hz 的频率采样，正弦波频率的镜像出现在采样频率整数倍的两边。
由于混叠频率为150Hz 。
镜像出现在0 ± 150, 600 ± 150, 1200 ± 150Hz......。
只有150、450、750Hz 在1kHz 以下。
当采样频率为550Hz 时，混叠频率为200Hz ，所以镜像出现在0 ± 50, 550 ± 200, 1100 ± 200Hz......。
只有200、350、750和900Hz 处在1kHz 以下。
与两者都一致的正弦波频率为750Hz 。
2.16 模拟电压范围为6V 。
(a) 量化步长为6/24 = 375 mV (b) 量化步长为6/28 = 23.44 mV (c) 量化步长为6/216 = 91.55 μV 2.17 (a) 28 = 256 (b) 210 = 1024 (c) 212 = 4096 2.18 量化映射一个无限模拟信号等级到一个有限数字信号等级，量化程度由使用的数位来决定。
对于任意有限数位，误差一定会出现，因为量化步长的大小是非零的。
下表标书了量化方法。
底端范围是步长的一半，顶端范围是步长的1.5倍。
所有其2.21量化值0111011001010100001100100001000011111110110111001011101010011000数字编码(a) 24.1 dB (b) 48.2 dB (c) 96.3 dB 2.23 动态范围为20 log (2N ) = 60.2 dB ，由此可以得出2N = 1023.29。
N 的值最靠近10，所以N 取10。
2.24 范围 = R, 量化步长 = QR = 1 V0.5Q = 0.1 V 因此, Q = 0.2 VR/Q = 2N = 5两个量化位(N = 2)不满足需求。
至少需要三个量化位(N=3)。
2.25 比特率=B bits/sample *f samples/sec=16*8000=128kbps 2.26 中间范围最大量化误差是量化步长Q 的一半。
对于范围R ，位数N 来说，步长为R/2N 因此。
将会保持量化误差在满意范围内。
消去R 然后解出N 为02.021N ≤，即502N ≥。
N 满足关系的最小值为N=6。
因此，最小比特率为Nf S = 6(16) = 96 kbps 。
2.27对于编码.2.28 抗镜像滤波器从零阶保持信号中移除了尖峰。
这样做之后，所有的奈奎斯特范围外的频率都被移除了。
但是滤波器引起了一个附加时延。
Chapter 3 Solutions3.1 (a) (i) x[0] = 3(ii) x[3] = 5(iii) x[–1] = 2(b) (i)(ii) x[n+1]3.2 冲激函数除了n=0处之外都是0(a) δ[–4] = 0(b) δ[0] = 1(c) δ[2] = 03.3 (a)、这个函数是冲激函数关于纵轴的镜像，没有其他改变。
(b) 这个函数是由冲激函数向右移两个单位得到，然后将它的振幅扩大一倍。
(c)3.4 阶跃函数对于n<0部分为0，其他部分为1。
(a) u[–3] = 0 (b) u[0] = 1 (c) u[2] = 13.5 (a) (b) (c) x[n] = 2u[–n]x[n]n(d)(e)3.6 (a)(b) x[n]=u[n]-u[n-2]3.7 (a)、这个信号是移动的阶跃函数之和。
每个增加一单位振幅。
(b)、这个信号一系列振幅增加的冲激信号之和。
3.8 x[n] = (u[n] – u[n–2]) + (u[n–5] – u[n–7]) + (u[n–10] – u[n–12])3.9 x[n] = 2δ[n] – 3δ[n –1] + δ[n –2] – δ[n –3] + 3δ[n –4] 3.10 (a)x[n] = δ[n –3] + δ[n –4] + δ[n –5] + δ[n –6] – δ[n –7] – δ[n –8] – δ[n –9] – δ[n –10] – δ[n –11] (b) x[n] = u[n –3] – 2u[n –7] + u[n –12] 3.11 x[n] = u[n] + 2u[n –4] 3.123.13 这个信号包括1, 0.5, 0.25,0.125,......。
这些能被0.5n 函数概值括，其中每个值是一个冲激信号的振幅。
这个信号也能表示成 ∑=-δ=0k k ]k n [)5.0(]n [x = δ[n] + 0.5δ[n –1] + 0.25δ[n –2] + 0.125δ[n –3] + …3.14(a) 利用欧拉公式 ⎪⎭⎫⎝⎛π-⎪⎭⎫ ⎝⎛π==π-4n sin j 4n cos e]n [x 4nj(b) 由(a)可知, 4π=Ω. 因此, 18422=ππ=Ωπ. 数字周期为8个采样点。
3.15 (a) ⎪⎫⎛π-⎪⎫ ⎛π==π-n sin j n cos e ]n [x 3n j(b)、复数的模式实部和虚部的平方和再开根号。
(a)中最后一列展示了3n j e π- = 1，这对所有的n 都成立。
3.16 模拟信号的频率为f = ω/2π = 200/2π Hz 。
采样频率为f S = 1/T S = 1/(25x10–3) = 40 Hz 。
数字频率为Ω = 2πf/f S = 200/40 = 5 rads 。
数字信号为x[n] = 5sin(n Ω) = 5sin(5n)。
3.17 检查每个函数的2π/Ω。
