试绘制闭环系统的根轨迹
- 格式:ppt
- 大小:7.63 MB
- 文档页数:229

第四章 根轨迹法4-1试粗略画出对应反馈控制系统具有以下前向和反馈传递函数的根轨迹图: ()()()()s s H s s s K s G 6.01,01.01.02+=++=4-2 试粗略地画出反馈系统函数 ()()()()2411+-+=s s s Ks G 的根轨迹。
4-3 对应负反馈控制系统,其前向和反馈传递函数为 ()()()()1,42)1(2=+++=s H s s s s K s G 试粗略地画出系统的根轨迹。
4-4 对应正反馈重做习题4-3,试问从你的结果中得出什么结论?4-5 试画出具有以下前向和反馈传递函数的,正反馈系统根轨迹的粗略图。
()()()()1,4122=++=s H s s Ks G4-6 试确定反馈系统开环传递函数为 ()()()()()5284)2(2+++++=s s s s s s K s H s G 对应-∞<K<∞的根轨迹。
指明所有根轨迹上的相应特征。
4-7 设一负反馈系统,其开环传递函数 ()()()()()90020040)4(2++++=s s s s s K s H s G a) 画出根轨迹并表明根轨迹上全部特征值。
b) 增益值在一个什么样的范围内,系统才是稳定的? c) 画出系统的伯德图,并使其稳定性和不稳定性区域,与根轨迹图连系起来说明。
4-8 对应负反馈情况,重做习题4-7.4-9 对应如下的负反馈控制系统,粗略地作出根轨迹,并确定系统稳定下K 的范围。
()()()()1,41)6(=+++=s H s s s s K s G4-10 对应习题4-10图所示系统,根据以下条件,试确定导致系统稳定的正实数增益K 的范围:a) 具有负反馈的系统。
b) 具有正反馈的系统。
习题4-10图4-11 已知反馈系统的开环传递函数*()()(1)(2)K G s H s s s s =++ 试绘制系统的根轨迹图,详细列写根轨迹的计算过程,其中包括零点、极点、渐近线及与实轴交点,根轨迹分离点及与虚轴的交点、渐近线与实轴夹角。
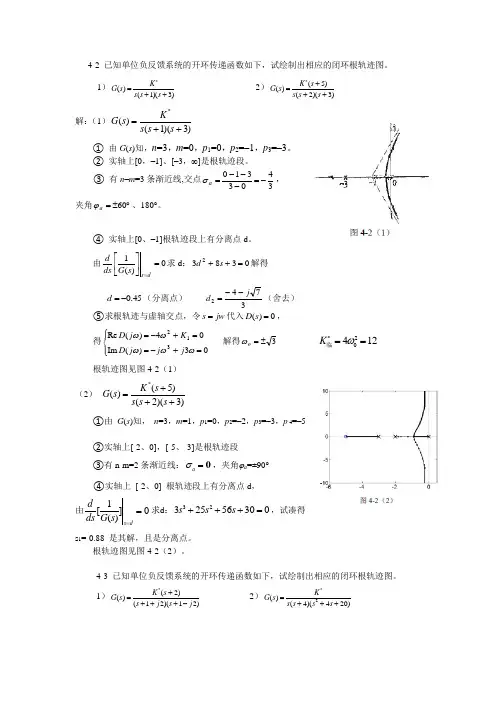
4-2 已知单位负反馈系统的开环传递函数如下,试绘制出相应的闭环根轨迹图。
1)*()(1)(3)K G s s s s =++ 2)*(5)()(2)(3)K s G s s s s +=++解:(1)()(1)(3)*K G s s s s =++① 由G (s )知,n =3,m =0,p 1=0,p 2=–1,p 3=–3。
② 实轴上[0,–1]、[–3,∞]是根轨迹段。
③ 有n –m =3条渐近线,交点3403310-=---=a σ, 夹角︒±=60a ϕ、180°。
④ 实轴上[0、–1]根轨迹段上有分离点d 。
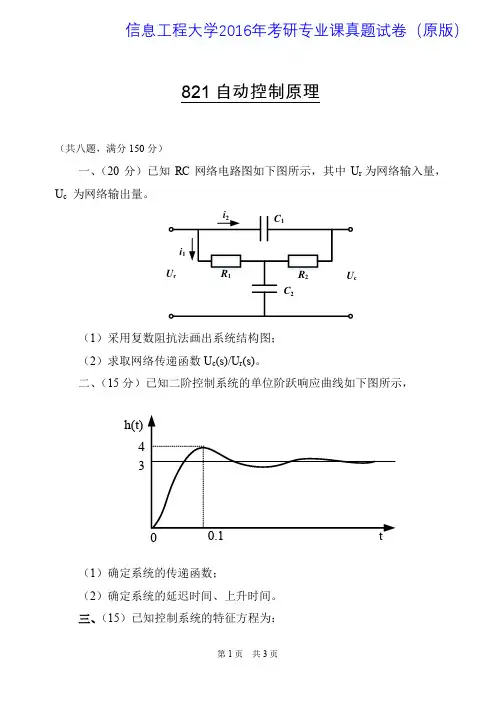
由0)(1=⎥⎦⎤⎢⎣⎡=ds s G ds d 求d :03832=++s d 解得 45.0-=d (分离点) 3742j d --=(舍去) ⑤求根轨迹与虚轴交点,令jw s =代入0)(=s D ,得⎪⎩⎪⎨⎧=+-==+-=03)(Im 04)(Re 312ωωωωωj j j D K j D 解得3±=o ω 20412*K ω==临根轨迹图见图4-2(1)(2) *(5)()(2)(3)K s G s s s s +=++①由 G (s )知, n =3,m =1,p 1=0,p 2=–2,p 3=–3,p 4=–5②实轴上[-2、0],[-5、-3]是根轨迹段 ③有n-m=2条渐近线:0a σ=,夹角ϕa =±90°④实轴上 [-2、0] 根轨迹段上有分离点d , 由1[]0()s dd ds G s ==求d :3232556300s s s +++=,试凑得 s 1=-0.88 是其解,且是分离点。
根轨迹图见图4-2(2)。
4-3 已知单位负反馈系统的开环传递函数如下,试绘制出相应的闭环根轨迹图。
1)*(2)()(12)(12)K s G s s j s j +=+++- 2)*2()(4)(420)K G s s s s s =+++解:(1)*(2)()(12)(12)K s G s s j s j +=+++-根轨迹图见图4-3(1)(2)*2()(4)(420)K G s s s s s =+++① n =4,m =0,p 1=0,p 2=–4,p 3、4=–2±j 4② p 1、p 2连线中点正好是p 3、p 4实部,开环极点分布对称于垂线s=–2,根轨迹也将对称于该垂线。



第三章3-1 已知二阶系统闭环传递函数为 369362++=s s G B 。
试求单位阶跃响应的t r , t m ,δ% , t s 的数值?解:[题意分析]这是一道典型二阶系统求性能指标的例题。
解法是把给定的闭环传递函数与二阶系统闭环传递函数标准形式进行对比,求出n ω参数,而后把n ω代入性能指标公式中求出r t ,m t ,%δ,s t 和N 的数值。
上升时间 t r峰值时间t m 过度过程时间t s 超调量δ%3-2 设单位反馈系统的开环传递函数为试求系统的性能指标,峰值时间,超调量和调节时间。
解:[题意分析]这是一道给定了开环传递函数,求二阶系统性能指标的练习题。
在这里要抓住二阶系统闭环传递函数的标准形式与参数(ζ,n ω)的对应关系,然后确定用哪一组公式去求性能指标。
根据题目给出条件可知闭环传递函数为与二阶系统传递函数标准形式2222nn n s s ωζωω++相比较可得12,12==n n ζωω,即n ω=1,ζ=0.5。
由此可知,系统为欠阻尼状态。
故,单位阶跃响应的性能指标为3-3 如图1所示系统,假设该系统在单位阶跃响应中的超调量%δ=25%,峰值时间m t =0.5秒,试确定K 和τK,τ与ζ,n ω的关系;%δ,m t 与ζ,nω 由系统结构图可得闭环传递函数为 与二阶系统传递函数标准形式相比较,可得由题目给定: %25%100%21=⨯=--ζζπδe即 25.021=--ζζπe两边取自然对数可得 依据给定的峰值时间: 5.012=-=ζωπn m t (秒)所以 85.615.02=-=ζπωn (弧度/秒)3-4 已知系统的结构图如图2所示,若)(12)(t t x ⨯= 时,试求:(1) 当τ=0时,系统的t r , t m , t s 的值。
(2) 当τ≠0时,若使δ%=20%,τ应为多大。
求出可得 )/(07.750秒弧度==n ω 由于ss X 2)(=输出的拉氏变换为 则拉氏反变换为(2) 当τ≠0时,闭环传递函数由 %20%100%21=⨯=--ζζπδe两边取自然对数 61.12.0ln 12-==--ζζπ, 可得故 73.85.)107.746.0(2=-⨯=o τ3-5(1) 什么叫时间响应答:系统在外加作用的激励下,其输出随时间变化的函数关系叫时间响应。


4-1 根轨迹法使用于哪类系统的分析?4-2 为什么可以利用系统开环零点和开环极点绘制闭环系统的根轨迹?4-3 绘制根轨迹的依据是什么?4-4 为什么说幅角条件是绘制根轨迹的充分必要条件?4-5 系统开零环、极点对根轨迹形状有什么影响?4-6 求下列各开环传递函数所对应的负反馈系统的根轨迹。
(1))2)(1()3()(+++=s s s K s W g K (2))2)(3()5()(+++=s s s s K s W g k (3) )10)(5)(1()3()(++++=s s s s K s W g k解:第(1)小题 由系统的开环传递函数)2)(1()3()(+++=s s s K s W g K 得知1. 起点:0=g K 时,起始于开环极点,即 11-=-p 、22-=-p2. 终点:=∝g K 时,终止于开环零点,31-=-z3. 根轨迹的条数,两条,一条终止于开环零点,另一条趋于无穷远。
4. 实轴上的根轨迹区间为3~-∝-和1~2--5. 分离点与会合点,利用公式0312111=+-+++d d d ()()()()()()()()()0321213132=+++++-+++++d d d d d d d d d 即:0762=++d d解上列方程得到:586.11-=d ,414.42-=d根据以上结果画出根轨迹如下图:解:第(2)小题 由系统的开环传递函数)2)(3()5()(+++=s s s s K s W g K 得知1. 起点:0=g K 时,起始于开环极点,即 00=-p 、21-=-p 、32-=-p2. 终点:=∝g K 时,终止于开环零点,51-=-z3. 根轨迹的条数,三条,一条终止于开环零点,另两条趋于无穷远。
4. 实轴上的根轨迹区间为3~5--和0~2-5. 分离点与会合点,利用公式05131211=+-++++d d d d 8865.0-=d6. 根轨迹的渐进线 渐进线倾角为:0009013)21(180)21(180 =-+=-+=μμϕm n 渐进线的交点为:01352311=--+=---=-∑∑==m n z p m i in j j k σ 根据以上结果画出根轨迹如下图:解:第(3)小题 由系统的开环传递函数)10)(5)(1()3()(++++=s s s s K s W g K 得知1. 起点:0=g K 时,起始于开环极点,即 10-=-p 、51-=-p 、102-=-p2. 终点:=∝g K 时,终止于开环零点,31-=-z3. 根轨迹的条数,三条,一条终止于开环零点,另两条趋于无穷远。

《自动控制原理》试卷(一)A一、)(/)(s R s C二、 系统结构图如图所示,τ取何值时,系统才能稳定 ?(10分)三、已知负反馈系统的开环传递函数为, 42)2()(2+++=s s s K s W k(1) 试画出以K 为参数系统的根轨迹;(2) 证明根轨迹的复数部分为圆弧 。
(15分)四、已知一单位闭环系统的开环传递函数为)15.0(100)(+=s s s W K ,现加入串联校正装置:101.011.0)(++=s s s W c ,试: (20分)(1) 判断此校正装置属于引前校正还是迟后校正?(2) 绘制校正前、后系统及校正装置的对数幅频特性。
(3) 计算校正后的相位裕量。
五、非线性系统结构如图所示,设输入r=0, 绘制起始点在0)0(,1)0(00==>=c cc c 的c c -平面上的相轨迹。
(15分)C )(s )(s o六、采样控制系统如图所示,已知: (15分)1.求出系统的开环脉冲传递函数。
2.当输入为)(1*)(1*)(1)(221t t t t t t r ++=时,求稳态误差ss e 。
七、用奈氏稳定判据判断如下图所示系统的稳定性。
其中,(1)─(3)为线性系统,(4)─(6)为非线性系统。
(15分)《自动控制原理》试卷(一)B一、 控制系统的结构如下图。
(1) 当F (s )=0时,求系统闭环传递函数)()()(s R s C s =Φ;(2) 系统中H 2(s )应满足什么关系,能使干扰F (s )对输出C (s )没有影响?(10分)二、. 设某控制系统方框图如图所示,要求闭环系统的特征值全部位于s =-1垂线之左,试确定参数K 的取值范围。
(10分)三、.一单位负反馈系统的开环传函为)15.0()125.0()(++=s s s K s W ,欲使该系统对单位阶跃函数的响应为一振幅按指数规律衰减的简谐振荡时间函数,试用根轨迹法确定K 值范围(要求首先绘制根轨迹,求出并在图上标注主要的特征点参数)。
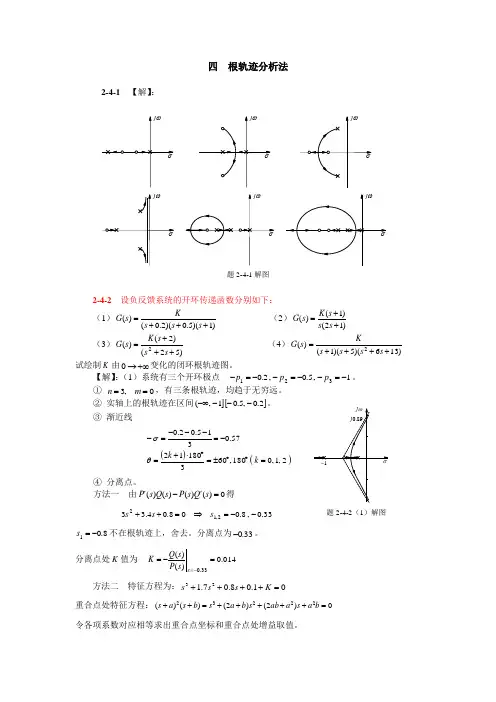
四 根轨迹分析法2-4-1 【解】:题2-4-1解图2-4-2 设负反馈系统的开环传递函数分别如下: (1))1)(5.0)(2.0()(+++=s s s Ks G (2))12()1()(++=s s s K s G(3))52()2()(2+++=s s s K s G (4))136)(5)(1()(2++++=s s s s Ks G试绘制K 由+∞→0变化的闭环根轨迹图。
【解】:(1)系统有三个开环极点 1,5.0,2.0321-=--=--=-p p p 。
① 0,3==m n ,有三条根轨迹,均趋于无穷远。
② 实轴上的根轨迹在区间]][2.0,5.01,(----∞。
③ 渐近线 ()()2,1,0180,6031801257.0315.02.0=︒︒±=︒⋅+=-=---=-k k θσ ④ 分离点。
方法一 由0)()()()(='-'s Q s P s Q s P 得33.0,8.008.04.332,12--=⇒=++s s s8.01-=s 不在根轨迹上,舍去。
分离点为33.0-。
分离点处K 值为 014.0)()(33.0=-=-=s s P s Q K方法二 特征方程为:01.08.07.123=++++K s s s重合点处特征方程:0)2()2()()(22232=+++++=++b a s a ab s b a s b s a s 令各项系数对应相等求出重合点坐标和重合点处增益取值。
题2-4-2(1)解图⑤ 根轨迹与虚轴的交点。
系统的特征方程为01.08.07.1)(23=++++=K s s s s D方法一 令ωj s +,得⎪⎩⎪⎨⎧=±=⇒⎪⎩⎪⎨⎧=++-=+-⇒=+++--26.18.001.07.108.001.08.07.12323K K K j j ωωωωωωω 方法二 将特征方程列劳斯表为Ks K s Ks s ++-+1.07.11.08.01.07.18.010123令1s 行等于0,得26.1=K 。
4-1 设单位反馈控制系统的开环传递函数 1)(+=∗s K s G试用解析法绘出∗K 从零变到无穷时的闭环根轨迹图,并判断下列点是否在根轨迹上: (-2+j0), (0+j1), (-3+j2) 解:有一个极点:(-1+j0),没有零点。
根轨迹如图中红线所示。
(-2+j0)点在根轨迹上,而(0+j1), (-3+j2)点不在根轨迹上。
4-2 设单位反馈控制系统的开环传递函数 )12()13()(++=s s s K s G 试用解析法绘出开环增益K 从零增加到无穷时的闭环根轨迹图。
解:系统开环传递函数为)2/1()3/1()2/1()3/1(2/3)(++=++=s s s K s s s K s g G 有两个极点:(0+j0),(-1/2+j0),有一个零点(-1/3,j0)。
根轨迹如图中红线所示。
4-3 已知开环零、极点分布如图4-28所示,试概略绘出相应的闭环根轨迹图。
图4-28 开环零、极点分布图4-4 设单位反馈控制系统开环传递函数如下,试概略绘出相应的闭环根轨迹图(要求确定分离点坐标d): (1) )15.0)(12.0()(++=s s s Ks G解:系统开环传递函数为)2)(5()2)(5(10)(++=++=s s s K s s s Ks g G 有三个极点:(0+j0),(-2+j0),(-5+j0)没有零点。
分离点坐标计算如下:051211=++++d d d 3解方程的010142=++d d 7863.31−=d ,d 88.02−=取分离点为88.0−=d根轨迹如图中红线所示。
(2) )12()1()(++=s s s K s G解:系统开环传递函数为)5.0()1()5.0()1(2/)(++=++=s s s K s s s K s g G有两个极点:(0+j0),(-0.5+j0),有一个零点(-1+j0)。
分离点坐标计算如下:115.011+=++d d d 解方程的05.022=++d d 7.11−=d ,d 29.02−=取分离点为7.11−=d ,29.02−=d 根轨迹如图中红线所示。
天津大学招收2011年硕士学位研究生入学考试试题考试科目名称:自动控制理论考试科目代码:812所有答案必须写在试卷纸上,并写清楚题号,答案写在试题上无效。
提示:本套考卷的部分试题对于学术型硕士研究生考生和全日制专业学位硕士研究生考生有所区别,前面未标注的试题为所有考生必答题,前面有标注的试题请考生务必选择相应类型试题作答,选错不得分。
一、(25分)某直流电机电枢电压输入uα与转角输出θm间满足的微分方程为(1)给出从电枢电压uα到电机转速间的传递函数,给出从电枢电压uα到电机转角θm间的传递函数,求时电机转速的稳态值。
(2)引入反馈控制式中为θr转角的给定值,求系统的闭环传递函数。
(3)为使闭环系统的超调量为16%,试确定K的取值,问此时系统的调节时间?二.(25分)已知被控对象由下列三个传递函数顺序串联而成(1)试将G1(S)、G2(S)、G3(S)的输出依次取状态变量X1、X2、X3,列写被控对象的状态方程描述。
(2)设计状态反馈矩阵K T=[k1,k2,k3],使系统的闭环极点为-3,-2±j2。
三.(25分)某单位反馈系统被控对象的传递函数为调节器的传递函数为(1)试绘制系统kp 从0到+∞、Ti从0到4两参数变化的根轨迹簇(具体绘图时取T=0.25、0.5、1、2、4)。
(2)根据根轨迹图,分别讨论kp 变化时、Ti变化时对系统闭环极点阻尼比和自然振荡频率的影响。
(3)谈论kp Ti=1、Ti变化时闭环系统的动态响应特性。
四.(25分)某单位反馈系统校正前的开环传递函数为要求校正后系统的加速度误差系数K a=31.6,系统开环传递函数中频段的斜率为-20dB /dec,函数穿越频率10rad/s,高频段的斜率为-40db/dec,且对频率为100rad/s的测量噪声扰动信号有-30dB的衰减。
(1)绘制希望的对数幅频特性曲线。
(2)给出校正装置的传递函数,它是一种什么校正装置?(3)计算校正前和校正后的系统相角裕度,定性说明系统的静态特性、稳定性和快速性的变化。
第三章3-1 已知二阶系统闭环传递函数为 369362++=s s G B 。
试求单位阶跃响应的t r , t m ,δ% , t s 的数值?解:[题意分析]这是一道典型二阶系统求性能指标的例题。
解法是把给定的闭环传递函数与二阶系统闭环传递函数标准形式进行对比,求出n ω参数,而后把n ω代入性能指标公式中求出r t ,m t ,%δ,s t 和N 的数值。
上升时间 t r峰值时间t m 过度过程时间t s 超调量δ%3-2 设单位反馈系统的开环传递函数为试求系统的性能指标,峰值时间,超调量和调节时间。
解:[题意分析]这是一道给定了开环传递函数,求二阶系统性能指标的练习题。
在这里要抓住二阶系统闭环传递函数的标准形式与参数(ζ,n ω)的对应关系,然后确定用哪一组公式去求性能指标。
根据题目给出条件可知闭环传递函数为与二阶系统传递函数标准形式2222nn n s s ωζωω++相比较可得12,12==n n ζωω,即n ω=1,ζ=0.5。
由此可知,系统为欠阻尼状态。
故,单位阶跃响应的性能指标为3-3 如图1所示系统,假设该系统在单位阶跃响应中的超调量%δ=25%,峰值时间m t =0.5秒,试确定K 和τK,τ与ζ,n ω的关系;%δ,m t 与ζ,nω 由系统结构图可得闭环传递函数为 与二阶系统传递函数标准形式相比较,可得由题目给定: %25%100%21=⨯=--ζζπδe即 25.021=--ζζπe两边取自然对数可得 依据给定的峰值时间: 5.012=-=ζωπn m t (秒)所以 85.615.02=-=ζπωn (弧度/秒)3-4 已知系统的结构图如图2所示,若)(12)(t t x ⨯= 时,试求:(1) 当τ=0时,系统的t r , t m , t s 的值。
(2) 当τ≠0时,若使δ%=20%,τ应为多大。
求出可得 )/(07.750秒弧度==n ω 由于ss X 2)(=输出的拉氏变换为 则拉氏反变换为(2) 当τ≠0时,闭环传递函数由 %20%100%21=⨯=--ζζπδe两边取自然对数 61.12.0ln 12-==--ζζπ, 可得故 73.85.)107.746.0(2=-⨯=o τ3-5(1) 什么叫时间响应答:系统在外加作用的激励下,其输出随时间变化的函数关系叫时间响应。
1. 已知单位反馈系统的开环传递函数,试绘制参数b从0→∞的根轨迹,并写出b=2时系统的闭环传递函数。
(1)(2)答案:[提示] 求等效开环传递函数,画根轨迹。
(1)分离点坐标:d1=-8.472,d2=0.472(舍),出射角θp=153.4°;(2)两支根轨迹,分离点的坐标-202. 已知系统的开环传递函数为(1)确信实轴上的分离点及K*的值;(2)确信使系统稳固的K*值范围。
答案:(1)实轴上的分离点d1=-1,d2=-1/3,对应的K*1=0,K2*=22/27;(2)稳固范围0<K*<63. 设单位负反馈系统的开环传递函数如下:(1)绘制系统准确的根轨迹图;(2)确信使系统临界稳固的开环增益K c的值;(3)确信与系统临界阻尼比相应的开环增益K。
答案:(1)分离点坐标:d1=-79(舍),d2=-21;(2)K c=150;(3)K=9.64. 设单位负反馈操纵系统开环传递函数已知,要求:(1)确信产生纯虚根的开环增益K;(2)确信产生纯虚根为±j1的z值和K*值。
答案:(1)用劳斯判据求临界稳固点得K*=110,化成开环增益K=11(2)将±j1任一点代入闭环特点方程得K*=30,z=199/305. 反馈系统的开环传递函数为试用根轨迹法确信出阶跃响应有衰减的振荡分量和无振荡分量时的开环增益K值范围。
答案:[提示] 特点根全为负实数时无振荡分量,为复数时有振荡分量6. 已知系统的特点方程为(1)s3+9s2+K*s+K*=0 (2)(s+1)(s+1.5)(s+2)+K*=0(3)(s+1)(s+3)+K*s+K*=0试绘制以K*为参数的根轨迹图。
答案:[提示] 将带K*项归并,方程两头同除不带K*项的多项式,求出等效的开环传函7. 已知单位反馈系统的开环传递函数为试绘制闭环系统的根轨迹图。
答案:[提示] 开环极点散布图分离点有3个,不要画错。