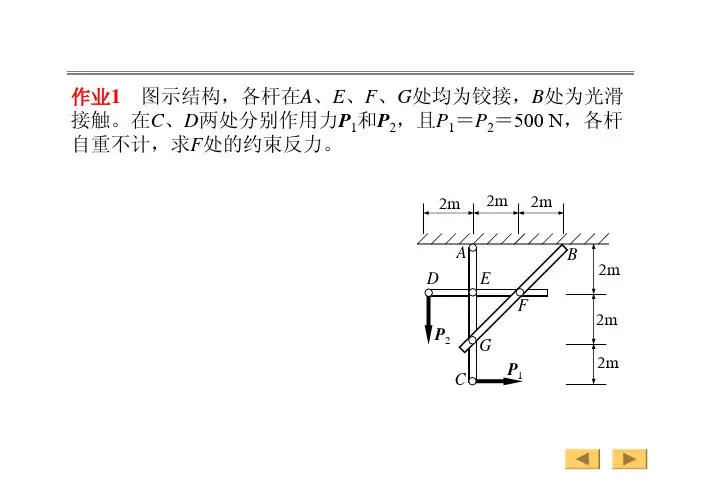
第二讲物体系统的平衡案例
- 格式:ppt
- 大小:2.44 MB
- 文档页数:44

第二讲 力平衡(一)精选例题【例1】 如图所示一个均匀的质量为1m 的球挂在天花板上,从同一点挂一个重物质量为2m 。
问所成角度。
O 【解析】相对于点的总力矩为0.)m g (l +R )sin =m 12g R -(l +R sin θθ⎡⎤⎣⎦∴()1212sin []+R m (m +)m R l θ-=该题如果用变力分析去解题,对悬挂2m 的绳对大球的支持力的方向比较困难,而用力矩去解题,显得尤为简单【例2】 如图,重为G 木块用绳子悬挂在两个轻杆支架的交点P ,现给木块一个水平方向的F F 12N 、N 、T 作用力,缓慢增大并且系统保持平衡,求作用力的变化趋势。
N 【解析】可以采用图解法,分别考虑木块以及P 点的受力平衡,将二者的受力三角形画在同一个图中,利用几何相似三角形的方法可以得到三个力的变化趋势。
最后可得,不变,2N 1和T 增加。
【例3】 如图,一个半径为R 非均匀质量光滑的圆球,其重心不在球心O 处,先将它置于A 30︒B A B 30︒C O 水平地面上,平衡时球面上的点和地面接触;再将它置于倾角为的粗糙斜面上,平衡时球面上的点与斜面接触,已知到的圆心角也为,试求球体的重心到球心的距离.【解析】B BC A OA 放在斜面上,球受重力支持力和摩擦力,三力共点必过点的重心在过B 于平面垂直的直线上。
即,又放在水平面上点落地,则此时球受重力和支持力,则球重心必在连线上,则重心位置在C 点.CO==【例6】有一长l重为W的均匀杆AB,A顶端竖直的粗糙墙壁上,杆端与墙间的摩擦系数μB CθμθP A P WPB PA x 为,端用一强度足够而不可伸长的绳悬挂,绳的另一端固定在墙壁点,木杆呈水平状态,绳与杆的夹角为(如图),求杆能保持平衡时与应满足的条件。
杆保持平衡时,杆上有一点存在,若与点间挂一重物,则足够大可以破坏平衡了,而在间任一点悬挂任意重物均不能破坏平衡。
求距离. 【解析】受力分析coT Nsθ=力平衡siT f W Wnθ+=+A力矩平衡:以为支点,θ=Wsin2lTl W+x∴f=W+W-N tan≤Nθμ2W xtanθ=+N W∴0002l2lW Wx xW+W Wtanlμθ-+()≤(+W)∴00()2l2W W)≤(+WtanlW Wx xμθ+-①0W=ntaμθ≥当不挂生物,此即为不挂重物平衡的条件,可得②W0(1)2tan(+1)-W Wμxμθl tanθ-+≤W取穷大,则上式仍成立.∴μθl tan(1)+-1tanxl tanθθμ+≥0⇒x≥wr G【例7】有一个半径为a,高为4a,重为的两端开口的薄壁圆筒,现将筒竖放在光滑的水平面上,之后将半径为,重为的两个完全相同的光滑圆球放入筒内而呈叠放状态,如图,当<r 2<a 2a 时,试求使圆筒不翻倒的条件.【解析】方法一:先看一个直角三角形O 对进行受力分析∴cos sin T =G cot θθ=N T θ=N G ⇒22212-a r ar -a r N =G ar -a sin θG =G =再对筒受力分析A N A 考虑以为支点,考虑翻倒则地面给筒的支持力的作用点移到点.则不翻倒条件。



物体的平衡条件的实例物体的平衡条件是物理学中一个重要的概念,用于描述物体处于平衡状态时所需的条件。
平衡条件分为静态平衡和动态平衡两种情况。
静态平衡是指物体处于静止状态时的平衡条件,而动态平衡则是指物体处于运动状态时的平衡条件。
下面将给出一些物体平衡条件的实例,以帮助我们更好地理解这个概念。
1. 静态平衡的实例1.1 悬挂的物体考虑一个质量为m的物体悬挂在一个绳子上,绳子与水平方向成为θ角度。
在静态平衡的情况下,物体所受的重力与绳子的拉力之间必须满足平衡条件。
根据平行四边形法则,可以得出以下关系:mgsinθ = T,其中g是重力加速度,T是绳子的拉力。
这个实例表明,只有当物体受到的拉力与重力平衡时,物体才能保持静态平衡。
1.2 支撑物体的力考虑一个物体放置在一个平坦的表面上并受到一些支撑力。
在静态平衡的情况下,物体所受的合力必须为零。
这意味着支撑物体的力必须平衡物体所受的重力。
例如,当我们将一本书放在桌子上时,桌子会施加一个向上的支撑力,以平衡书受到的向下的重力。
只有当支撑力与重力平衡时,桌子和书才能保持静态平衡。
2. 动态平衡的实例2.1 旋转的物体考虑一个物体以角速度ω围绕一个固定轴旋转。
在动态平衡的情况下,物体所受的合力矩必须为零。
这意味着物体所受的合力与轴之间的垂直距离(也称为杠杆臂)的乘积必须相等以平衡力矩。
举个例子,当我们旋转一个旋转木马时,我们需要在使得旋转木马保持平衡的同时,保持给它一个适当的推动力。
2.2 运动物体的平衡考虑一个物体在水平面上运动,通过作用力施加在物体上。
在动态平衡的情况下,物体所受的合力必须为零。
这意味着作用在物体上的力必须平衡物体所受的摩擦力和空气阻力。
例如,在推动一辆自行车时,我们需要平衡我们施加在脚踏板上的力与空气阻力和摩擦力,以保持自行车的平衡状态。
以上是一些物体平衡条件的实例。
无论是静态平衡还是动态平衡,物体都必须符合特定的平衡条件才能保持平衡状态。

受力分析及物体平衡典型例题解析在物理学中,受力分析和物体平衡是非常重要的基础知识。
通过对物体所受力的分析,我们可以了解物体的运动状态以及是否处于平衡状态。
本文将通过解析几个典型的例题,帮助读者更好地理解受力分析和物体平衡的概念。
例题一:垂直轴上的物体平衡将一个质量为10千克的木块悬挂在一根质量忽略不计的轻杆上,轻杆的一端固定在墙上,另一端与滑轮相连,滑轮距地面高度为2米。
现求木块上挂的重物的质量是多少?解析:首先,我们可以根据题目中给出的物体的质量和距离,得到所受到的重力,即10千克 * 9.8米/秒² = 98牛顿。
由于木块处于静止状态,根据角动量守恒定律,木块所受合力矩为零。
由于轻杆质量忽略不计,可以将滑轮视为质量忽略不计的点,即滑轮为定轴。
设木块上挂的重物的质量为M,根据力矩平衡公式有:2米 * 98牛顿 - 0米 * M = 0解得:M = 98千克所以,木块上挂的重物的质量为98千克。
例题二:倾斜面上的物体平衡一个质量为5千克的木箱被放置在一个倾角为30°的光滑斜面上,斜面上有一垂直向上的力F使木箱处于静止状态,求力F的大小。
解析:首先,我们可以根据题目中给出的物体的质量和斜面的倾角,得到物体所受到的重力,即5千克 * 9.8米/秒² = 49牛顿。
由于木箱处于静止状态,根据 Newton's第一定律,合力等于零。
这意味着斜面上的力F必须与斜面的竖直方向的分量相抵消。
设力F的大小为F1,根据受力分析,可以得到以下等式:F1 * cos30° = 49牛顿解得:F1 = 98牛顿所以,力F的大小为98牛顿。
例题三:悬挂物体和支撑力的分析一个质量为2千克的物体用绳子悬挂在天花板上,绳子的倾角为60°,求绳子的拉力和天花板对物体的支撑力。
解析:首先,根据题目中给出的物体的质量和绳子的倾角,可以得到物体所受到的重力,即2千克 * 9.8米/秒² = 19.6牛顿。
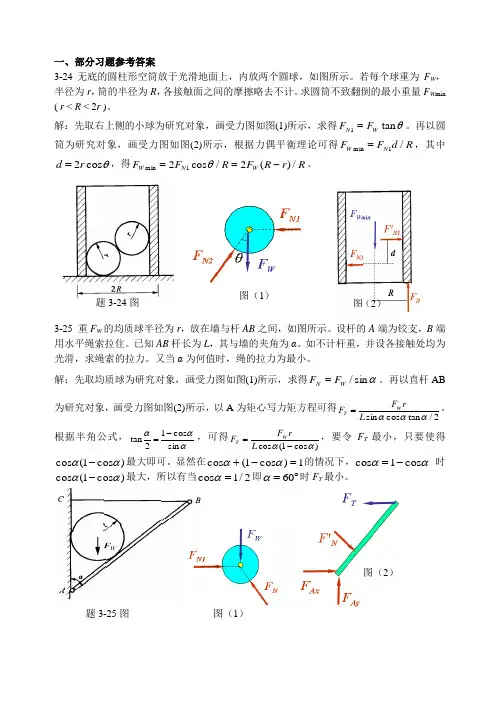
题3-24图 一、部分习题参考答案3-24无底的圆柱形空筒放于光滑地面上,内放两个圆球,如图所示。
若每个球重为F W ,半径为r ,筒的半径为R ,各接触面之间的摩擦略去不计。
求圆筒不致翻倒的最小重量F W min( r < R < 2r )。
解:先取右上侧的小球为研究对象,画受力图如图(1)所示,求得θtan 1W N F F =。
再以圆筒为研究对象,画受力图如图(2)所示,根据力偶平衡理论可得R d F F N W /1min =,其中θcos 2r d =,得R r R F R F F W N W /)(2/cos 21min -==θ。
3-25 重F W 的均质球半径为r ,放在墙与杆AB 之间,如图所示。
设杆的A 端为铰支,B 端用水平绳索拉住。
已知AB 杆长为L ,其与墙的夹角为α。
如不计杆重,并设各接触处均为光滑,求绳索的拉力。
又当α为何值时,绳的拉力为最小。
解:先取均质球为研究对象,画受力图如图(1)所示,求得αsin /W N F F =。
再以直杆AB为研究对象,画受力图如图(2)所示,以A 为矩心写力矩方程可得2/tan cos sin αααL r F F W T =。
根据半角公式,αααsin cos 12tan -=,可得)cos 1(cos αα-=L r F F W T ,要令F T 最小,只要使得)cos 1(cos αα-最大即可。
显然在1)cos 1(cos =-+αα的情况下,ααcos 1cos -= 时)cos 1(cos αα-最大,所以有当2/1cos =α即︒=60α时F T 最小。
题3-25图图(2) 图(1)图(1) 图(2)3-29图示闸门纵向桁架承受宽2m 的面板水压力,设水深与闸门顶齐平,试求桁架各杆内力。
【解】各部分受力分析和计算结果如题3-29所示。
二、典型例题解答1、如图1(a )所示,已知F 1=150N ,F 2=200N ,F 3=300N ,F =F'=200N 。
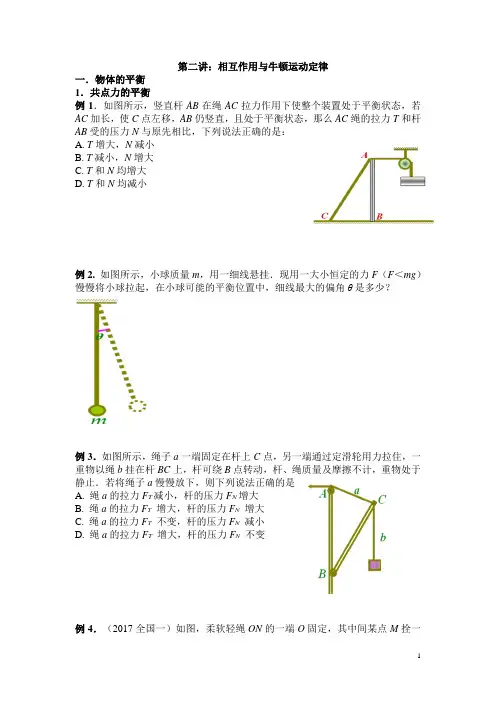
第二讲:相互作用与牛顿运动定律一.物体的平衡1.共点力的平衡例1.如图所示,竖直杆AB在绳AC拉力作用下使整个装置处于平衡状态,若AC加长,使C点左移,AB仍竖直,且处于平衡状态,那么AC绳的拉力T和杆AB受的压力N与原先相比,下列说法正确的是:A. T增大,N减小B. T减小,N增大C. T和N均增大D. T和N均减小例2. 如图所示,小球质量m,用一细线悬挂.现用一大小恒定的力F(F<mg)慢慢将小球拉起,在小球可能的平衡位置中,细线最大的偏角θ是多少?例3.如图所示,绳子a一端固定在杆上C点,另一端通过定滑轮用力拉住,一重物以绳b挂在杆BC上,杆可绕B点转动,杆、绳质量及摩擦不计,重物处于静止.若将绳子a慢慢放下,则下列说法正确的是A. 绳a的拉力F T减小,杆的压力F N增大B. 绳a的拉力F T增大,杆的压力F N增大C. 绳a的拉力F T不变,杆的压力F N减小D. 绳a的拉力F T增大,杆的压力F N不变例4.(2017全国一)如图,柔软轻绳ON的一端O固定,其中间某点M拴一重物,用手拉住绳的另一端N。
初始时,OM竖直且MN被拉直,OM与MN之间的夹角为α(π2α>)。
现将重物向右上方缓慢拉起,并保持夹角α不变。
在OM由竖直被拉到水平的过程中A.MN上的张力逐渐增大B.MN上的张力先增大后减小C.OM上的张力逐渐增大D.OM上的张力先增大后减小例5.如图所示,在绳下端挂一质量为m的物体,用力F拉绳使悬绳偏离竖直方向α角,当拉力F与水平方向的夹角θ多大时F有最小值?最小值是多少?例6.(2012新课标卷)拖把是由拖杆和拖把头构成的擦地工具(如图)。
设拖把头的质量为m,拖杆质量可以忽略;拖把头与地板之间的动摩擦因数为常数μ,重力加速度为g,某同学用该拖把在水平地板上拖地时,沿拖杆方向推拖把,拖杆与竖直方向的夹角为θ。
(1)若拖把头在地板上匀速移动,求推拖把的力的大小。
(2)设能使该拖把在地板上从静止刚好开始运动的水平推力与此时地板对拖把的正压力的比值为λ。


力学中的平衡问题案例研究案例一:悬挂绳的平衡在力学中,悬挂绳是一个常见的平衡问题。
一根悬挂绳由两端固定在支撑物上,中间悬挂一个物体。
我们需要研究该物体在不同条件下的平衡情况。
首先,我们考虑悬挂绳的自身重力。
如果绳的质量非常轻微,可以忽略不计,那么物体在绳的中间位置会保持平衡。
这是因为绳的重力对物体施加的力平衡,使得物体保持静止。
然而,当绳的质量较大时,绳的自身重力将对物体产生倾斜力。
这会导致物体向下滑动,直到产生一个平衡点。
在这个平衡点上,绳的自身重力和物体的重力相互平衡,使得物体保持静止。
案例二:平衡质点的受力分析另一个力学中的平衡问题涉及平衡质点的受力分析。
当一个物体处于静止状态时,所有施加在它上面的力都必须平衡,即合力为零。
我们可以考虑一个简单的例子,一个放置在桌子上的书本。
在这种情况下,书本受到桌子的支持力和重力的作用。
桌子的支持力向上,与重力方向相反,使得书本保持静止。
除了支持力和重力,还可能存在其他的力,如摩擦力或弹簧力等。
研究平衡质点的受力分析可以帮助我们理解物体如何保持平衡,并计算各个力的大小和方向。
案例三:平衡物体的转动点平衡物体的转动是力学中另一个重要的平衡问题。
当一个物体绕某个点旋转时,我们可以研究该点的平衡情况。
考虑一个平衡在杠杆上的物体。
在这种情况下,物体绕着杠杆的转动点进行旋转。
通过力矩平衡的原理,我们可以得出物体保持平衡的条件。
物体保持平衡的关键是杠杆上的力矩和力矩的和为零。
这意味着物体的重力矩和其他力所产生的力矩互相平衡,使得物体保持静止。
总结起来,力学中的平衡问题案例研究涉及悬挂绳的平衡、平衡质点的受力分析和平衡物体的转动点。
通过研究这些案例,我们可以更好地理解力学中的平衡问题,并应用相关原理解决实际问题。
800字以上。
初中一年级物理实践教学案例探索简单的平衡原理在初中一年级的物理学习中,学生们需要通过实践活动来深入理解和应用所学的知识。
本文将介绍一个针对平衡原理的实践教学案例,旨在帮助学生们更好地理解和掌握该概念。
实践活动名称:小球探秘实践目标:通过观察和实践活动,让学生们了解平衡原理的基本概念,并能够运用所掌握的知识解释实际生活中的现象。
实践材料:1. 一个平衡木或者一个长而细的木棍2. 三个大小相同的小球3. 一块毛巾或者软布实践活动步骤:步骤一:引导学生思考通过小组讨论的方式,引导学生思考以下问题:1. 什么是平衡?你们如何理解平衡?2. 平衡与物体在空间位置上的关系是什么?3. 平衡与物体的质量有关系吗?步骤二:实践活动开始1. 将平衡木或木棍平放在桌子上,确保它处于平衡状态。
2. 在平衡木的一端放置一个小球,观察平衡木是否保持平衡。
3. 将这个小球移动到平衡木的中间位置,再次观察平衡木是否保持平衡。
4. 将这个小球移动到平衡木的另一端,观察平衡木是否保持平衡。
5. 通过实践观察,让学生们探索平衡原理,并记录自己的观察结果和体会。
步骤三:探索与总结1. 学生们通过观察和实践,会发现当小球在平衡木上的不同位置时,平衡木是否保持平衡。
2. 引导学生分析实践结果,得出结论:平衡木保持平衡的条件是质量相等的物体在平衡木上的距离相等。
3. 让学生们讨论和总结平衡原理的基本概念和作用。
步骤四:扩展活动为了进一步巩固学生对平衡原理的理解,可以设计一些扩展活动,例如:1. 将两个大小不同的小球放在平衡木上,观察平衡木是否保持平衡,让学生分析其中的原因。
2. 在平衡木的一端加上一块重物,观察平衡木是否保持平衡,引导学生思考平衡原理在实际生活中的应用。
通过以上实践活动,学生们可以直观地感受到平衡原理的作用,提高他们的学习兴趣和动手实践能力。
同时,通过观察和分析实践结果,他们也能够更深入地理解平衡原理的基本概念和应用。
总结:通过这个物理实践教学案例,初中一年级的学生们可以通过观察和实践,探索简单的平衡原理。