工程力学第4节 静定问题与物体系统的平衡
- 格式:ppt
- 大小:624.00 KB
- 文档页数:10





第4章 刚体和刚体系统的平衡4-1 质点系和刚体的平衡条件例1:如图所示的平面刚架,在B 点处受到一水平力P =20kN 的作用,刚架自重不计,试求A 、D 处的约束力。
解:(1)选刚架为研究对象。
(2) 画受力图。
根据三力汇交定理,RA 的指向如图所示。
(3) 列平衡方程。
0548∑=+=A R P X 05440∑=+=A D R R Y kN 4.22-25-==P R AkN 1051-==A D RR例2:梁AB 受一力偶作用,其矩m = -100kN·m 。
尺寸如图所示,试求支座A 、B 的反力。
解:(1)取梁AB 为研究对象2)画受力图 由支座A 、B 的约束性质可知,RB 的作用线为垂直方向,而RA 的作用线方向不定。
由于力偶只能与力偶相平衡,因此力RA 与力RB 必定组成一个力偶,其大小满足RA=RB ,指向如图所示。
3)列平衡方程求未知量 由平面力偶系的平衡方程有:例3:在水平梁AB 上作用一力偶矩为M 的力偶,在梁长的中点C 处作用一集中力P 它与水平的夹角为θ ,如图所示。
梁长为l 且自重不计。
求支座A 和B 的反力。
解:取水平梁AB 为研究对象,画受力图。
例4:水平外伸梁AB ,若均布载荷q =20kN/m ,P =20kN ,力偶矩m =16kN·m ,a =0.8m 。
求支座A 、B 处的约束力。
AkNR R kN R m R M A B A A 2020050i ===⇒=-=∑0cos -F 0A ∑==θP X x θcos F A P x =0F 2sin -M -0)(∑=+∙=l l P F M B i A θ2sin M F θP l B +=0F -2sin M-0)(A B ∑=∙+=l l P F M y i θ2sin M -F A θP l y +=解:(1)选梁AB 为研究对象,画受力图。
(2)属于平面平行力系,列方程求解未知量。



工程力学中的静力学平衡与结构平衡问题工程力学是研究物体静止或运动状态下受力和变形的学科。
而静力学平衡和结构平衡问题是工程力学的重要内容之一。
本文将探讨静力学平衡的基本原理和结构平衡的相关概念。
一、静力学平衡问题静力学平衡问题是指研究物体在不发生运动的情况下的受力平衡情况。
在静力学平衡问题中,物体所受外力和外力对物体的作用点位矢量之和为零,即∑F = 0。
这是基于牛顿第一定律的,物体处于静止或匀速直线运动状态时,所受合力为零。
在解决静力学平衡问题时,常使用力的合成与分解原理以及受力分析的方法。
通过分析物体所受的各个力的作用方向和大小,可以确定物体所处的平衡状态。
静力学平衡问题的应用很广泛,比如在建筑工程中,我们需要确保建筑物的稳定性。
通过分析各个构件所受的力和力矩,可以确定建筑物的结构是否平衡,从而保证其安全性。
二、结构平衡问题结构平衡问题是指研究物体内部各个构件的受力平衡情况。
在解决结构平衡问题时,需要考虑物体内部的各个节点和构件之间的相互作用关系。
结构平衡问题可以通过静力学平衡的原理来解决。
对于一个构件而言,其受力平衡要求总力合为零。
在力的合成与分解原理的帮助下,可以确定每个节点上的力的大小和方向,从而得到整个结构的受力平衡状况。
在实际工程中,结构平衡问题是保证建筑物和桥梁等工程结构稳定性的重要问题。
通过分析结构的受力平衡情况,可以确定结构的合理设计,并且预测结构在受到外力作用时的变形情况,从而确保结构的安全性。
三、应用实例为了更好地理解工程力学中的静力学平衡与结构平衡问题,我们举一个简单的桥梁的实例。
考虑一座桥梁,桥上有一辆汽车在通过。
我们需要确保桥梁的结构平衡以保证安全。
首先,我们可以将桥梁简化为若干个构件,比如桥墩、桥面等。
通过静力学平衡原理,我们可以分析每个构件所受的受力情况。
以桥墩为例,桥墩受到来自桥面和汽车的作用力。
通过力的合成与分解原理,我们可以确定桥墩所受力的大小和方向。
类似地,我们可以对桥面和其他构件进行受力分析。

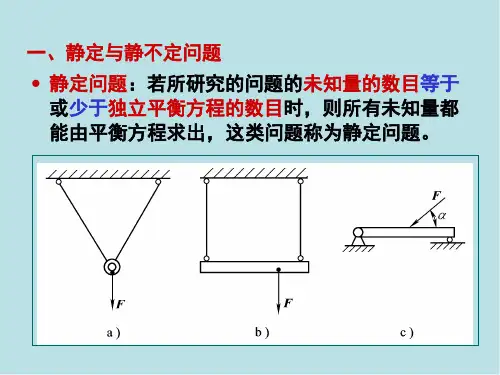
物体系统的平衡静定与静不定(超静定)问题•静定与超静定(静不定)的概念对每一种力系而言,若未知量的数目等于独立平衡方程的数目。
则应用刚体静力学的理论,就可以求得全部未知量,这样的问题称为静定问题。
(理论力学)若未知量的数目超过独立平衡方程的数目,则单独应用刚体静力学的理论,就不能求出全部未知量,这样的问题称为静不定问题(超静定问题)。
(材料力学等)静定:未知量个数等于独立的平衡方程数;未知量的数目=独立平衡方程的数目静不定(超静定):未知量个数大于独立的平衡方程数。
未知量的数目> 独立平衡方程的数目超静定次数:未知量个数与独立的平衡方程数之差。
当研究对象中未知约束力个数小于独立的平衡方程数时,其运动状态一般都是变化的,工程中将这样的力学系统称为机构,这种情况在工程结构设计中是应该避免的。
具有n个物体组成的平面静定物体系统:最多3n个独立平衡方程,求解3n个未知量。
超静定问题:材料力学原理建立补充方程求解。
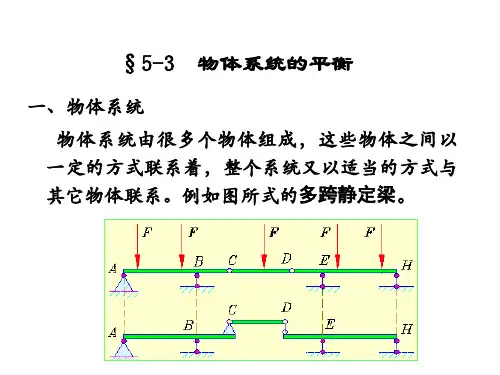
A BPF PF PF判断各图示结构的静定性•刚体系统(物体系统)的平衡问题1. 两个或两个以上刚体用一定的方式连接起来组成的系统,称为刚体系统;2. 刚体系统整体处于平衡时,每一局部均处于平衡。
局部:组成系统的单个或几个刚体所构成的子系统。
0A M =∑0D M =∑0C M =∑0B M =∑∑=0X 0=∑Y 刚体系统平衡问题的特点是:仅仅考察系统整体平衡,一般无法求得全部未知力。
1m 1m q pF F 1A 0.5m 0.5m (a)1m1m D B C Q Ax F Ay F M A BF P1.一般解法:编程,运用计算机求解线性代数方程组。
对于每个刚体都受平面任意力系作用的刚体系统,总可以建立3n个独立的平衡方程。
如果系统是静定的,也应有相同个数的未知量,最终就归结为求解线性代数方程组的问题,利用高斯消元法等方法,总能在计算机上程式化地实现数值求解。
2.分析解法:由于许多工程实际问题并不需要求出刚体系统的所有内部和外部的约束力,而通常只需求出某一部分的约束力,因此,利用分析解法以简化运算是必要的。