2.1从平面向量到空间向量课件(北师大版高中数学选修2-1)
- 格式:ppt
- 大小:822.00 KB
- 文档页数:21







高考数学选修2,1知识点:从平面向量到空间向量1500字从平面向量到空间向量,是高中数学的一个重要知识点。
平面向量和空间向量是向量的两种不同形式,它们在数学上有着相似的性质和运算规律,但在几何上有一些区别。
首先,我们来了解一下平面向量。
平面向量是指在平面内有大小和方向的向量。
平面向量用有向线段表示,线段的方向表示向量的方向,线段的长度表示向量的大小。
设向量AB的起点为A,终点为B,记作向量AB,表示为→AB。
平面向量有两种表示方法:坐标表示和分量表示。
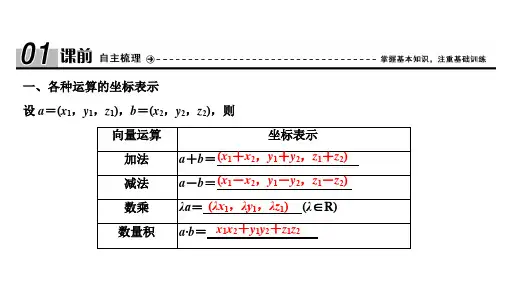
1. 坐标表示:假设平面向量AB的起点坐标为A(x1, y1),终点坐标为B(x2, y2),则向量AB的坐标表示为(x2 - x1, y2 - y1)。
2. 分量表示:平面向量的分量表示是通过向量的水平分量和竖直分量表示向量。
假设平面向量AB的长度为|r|,与X轴的夹角为θ,则水平分量为|r|cosθ,竖直分量为|r|sinθ。
接下来,我们来了解一下空间向量。
空间向量是指在三维空间中有大小和方向的向量。
空间向量同样用有向线段表示,线段的方向表示向量的方向,线段的长度表示向量的大小。
设向量AB的起点为A,终点为B,记作向量AB,表示为→AB。
空间向量也有两种表示方法,即坐标表示和分量表示。
1. 坐标表示:假设空间向量AB的起点坐标为A(x1, y1, z1),终点坐标为B(x2, y2, z2),则向量AB的坐标表示为(x2 - x1, y2 - y1, z2 - z1)。
2. 分量表示:空间向量的分量表示同样是通过向量在坐标轴上的投影来表示向量。
假设空间向量AB的长度为|r|,与X轴、Y轴、Z轴的夹角分别为α、β、γ,则向量的X 轴分量为|r|cosα,Y轴分量为|r|cosβ,Z轴分量为|r|cosγ。
在从平面向量到空间向量的过程中,需要注意以下几点:1. 坐标表示的差异:平面向量的坐标表示有两个分量,而空间向量的坐标表示有三个分量。
2. 分量表示的差异:平面向量的分量表示只有水平分量和竖直分量,而空间向量的分量表示有X轴、Y轴、Z轴三个分量。

从平面向量到空间向量一、设计思路本节是北师大版高中数学选修2-1第二章第一节内容,学生已经学习了平面向量和空间几何体及其点线面位置关系,本章是平面向量的推广和延伸,是解决空间问题的有力工具.学生是学习的主体,本节课注重给学生提供各种参与机会:通过自学,小组讨论,多媒体展示,最大程度地激发学生参与教学的过程.结合教材以及本班学生情况,本节教学内容设计为两个部分,第一部分是向量的概念,着重学生自学与合作后的展示.通过与平面向量的类比,引入空间向量的相应概念:空间向量、向量的表示、自由向量、向量的模、向量,的夹角等.第二部分是向量、直线、平面,主要由教师引导完成教学内容.通过分析向量与直线,向量与平面的位置关系,引入直线l的方向向量,平面 的法向量等概念.通过这两部分的设计,降低学生的理解难度,突出了类比的数学思想方法.二、教学目标1. 知识与技能:(1)了解空间向量的有关概念;(2)掌握两个空间向量的夹角、方向向量和平面的法向量的概念.2. 过程与方法:经历向量从平面到空间推广的过程,分析向量与直线、平面的位置关系,让学生学会类比的数学思想方法.3. 情感与态度:尝试解决问题过程中,让学生树立类比分析、循序渐进解决数学问题的能力;借助直观模型,让学生感受从感性到理性,从具体到抽象的研究问题的方法.三、教学重点及处理设想理解向量的夹角、直线的方向向量、平面的法向量等概念.借助平面向量以及空间平行概念的基础,对向量的概念从维度(二维平面到三维空间)进行推广,可让学生从周围的几何体(长方体模型,教室等)培养学生的空间想象能力. 四、教学难点及处理设想理解共面向量的概念.对于空间两个向量都是共面向量的认同,处理设想为可以借助空间异面直线的概念提出空间两向量是否可能异面的问题,继而结合自由向量和相等向量的概念来解决.五、教学方法导学法,讨论法.六、教学准备学生学案,多媒体课件.七、教学流程设计2.学案导学(学案详见附1)知识要点:(1)空间向量的有关概念空间向量的概念及表示自由向量向量的模(或长度)④向量a,b的夹角、X围及垂直与平行(共线)⑤单位向量⑥零向量⑦相等向量⑧相反向量⑨共面向量(2)向量、直线、平面激励主动学习,培养自主探究能力.(1)对于让学生感受到维度改变(平面到空间)对概念产生的影响,培养类比的意识;对于④⑤⑥⑦⑧让学生感受直接由平面向量类比得到空间向量的相关概念所得到的成就感;对于⑦结合数量适时引出“向量不能比较大小”的结论;对于④直线l的方向向量平面α的法向量适时回顾区分向量与异面直线的夹角概念的区别,对于⑦引出“空间任何两个向量都共面”的结论.(2)对于直线的方向向量与平面的法向量主要由教师随后引导完成概念教学.5.教师引导性讲解向量、直线、平面直线l的方向向量平面 的法向量借助多媒体向同学引入直线的方向向量和平面的法向量的概念,并且完成问题(7)(8).八、教学反思1.《新课程标准》中要求让学生经历向量及其运算由平面向空间推广的过程,目的是让学生体会数学的思想方法(类比与归纳),体验数学在结构上的和谐性与在推广过程中的问题,并尝试如何解决这些问题.同时在这一过程中,也让学生见识一个数学概念的推广可能带来很多更好的性质.掌握空间向量的基本概念及其性质是基本要求.空间向量为处理立体几何问题提供了新的视角,空间向量的基本概念是后续学习的前提,空间向量是平面向量的推广,空间向量及其运算所涉及的内容与平面向量及其运算相似,所以,空间向量的教学要注重知识间的联系,温故而知新,运用类比的方法认识新问题,经历向量及其运算由平面向空间推广的过程.2.教师的教学实际上就是保证和促进学生学习的主动性和知识体系的建构.本节课尝试让学生自主学习,主要过程包括:(1)预习交流——学生按照“学案”进行课前预习或当堂预习交流;(2)小组讨论——根据自学任务小组进行讨论交流,完成预期任务;(3)展示交流——各组根据组内讨论情况,对本组的学习任务进行讲解展示;(4)穿插巩固——在展示过程中,对未能展现的学习任务进行巩固练习.(5)学后反思——对学习过程中的感受进行总结.。

高二数学选修2-1 空间向量的运算及空间向量的基本定理 北师大版(理) 【本讲教育信息】 一、教学内容:选修2-1 空间向量的运算及空间向量的基本定理二、教学目标:1. 理解并掌握空间两个向量的夹角、直线的方向向量、平面的法向量、共面向量等基本概念。
2. 熟练地掌握空间向量的加减运算、数乘运算、空间向量坐标运算的运算法则、运算律及空间向量的数量积的几何意义及性质。
3. 熟练地掌握共线向量定理、空间向量的基本定理,并能利用它们讨论证明空间的线面关系。
4. 体会用类比的数学思想、方程的数学思想、等价转化的数学思想解决问题。
三、知识要点分析:(一)平面向量与空间向量的相同点:1. 向量夹角:过空间一点O 作AOB ,OB b ,OA a ∠==则是向量a 与向量b 的夹角。
X 围:[0,]π2. 加减运算:加减运算法则:向量的平行四边形法则(三角形法则) 运算律:结合律:)()(c b a c b a ++=++,交换律:a b b a +=+3. 数乘运算法则:向量a 与实数λ的乘积是一个向量,记作:a λ,满足(i )||||λλ=a ||a ,(ii )当0>λ时,a λ与a 方向相同,反之,相反。
0a 0=λ=λ时,。
运算律:(i )).(,R a a ∈=λλλ(ii ))R ,(,a a a )(,b a )b a (∈μλμ+λ=μ+λλ+λ=+λ.(iii )),(),()(R a a ∈=μλμλλμ4. 空间向量的数量积:θ⋅=⋅cos |b ||a |b a 。
θ>=<b a ,。
运算律:交换律:a b b a ⋅=⋅分配律:c a b a )c b (a ⋅+⋅=+⋅,(λ)b a ⋅=b )a (⋅λ)b (a λ⋅=性质:(1)a a |a |⋅,(2)0b a b a =⋅⇔⊥,(3)|b ||a ||b a |⋅≤⋅注:向量的数量积运算不满足乘法的结合律。
【成才之路】2021-2021学年高中数学 2.1 从平面向量到空间向量基础达标 北师大版选修2-1一、选择题1.假设空间向量a 与向量b 不相等,那么a 与b 必然( )A .有不同的方向B .有不相等的模C .不可能是平行向量D .不可能都是零向量[答案] D[解析] a ,b 不相等,可能方向不同,也可能模不相等,因此A ,B ,C 都不正确,只有D 正确.2.假设命题M :AA ′→=BB ′→;命题N :四边形ABB ′A ′是平行四边形,那么M 是N 的( )A .充分没必要要条件B .必要不充分条件C .充要条件D .既不充分又没必要要条件 [答案] B[解析] 由四边形ABB ′A ′是平行四边形,可得AA ′→=BB ′→.可是由AA ′→=BB ′→,只能说明AA ′→与BB ′→是相等向量,AA ′→与BB ′→所在的直线可能平行或共线,并非必然组成平行四边形ABB ′A ′,因此M 是N 的必要不充分条件.3.在平行六面体ABCD —A 1B 1C 1D 1中,向量D 1A →、D 1C →、A 1C 1→是( )A .有相同起点的向量B .等长向量C .共面向量D .不共面向量 [答案] C[解析] 先画出平行六面体的图像,可看出向量D 1A →、D 1C →在平面ACD 1上,由于向量A 1C 1→平行于AC →,因此向量A 1C 1→通过平移能够移到平面ACD 1上,因此向量D 1A →、D 1C →、A 1C 1→为共面向量.二、填空题4.以下有关平面法向量的说法中,正确的选项是________(填写相应序号).①平面α的法向量垂直于与平面α平行的所有向量;②一个平面的所有法向量相互平行;③若是两个平面的法向量垂直,那么这两个平面也垂直;④若是a ,b 与平面α平行,且n ⊥a ,n ⊥b ,那么n 确实是平面α的一个法向量.[答案] ①②③[解析] 当a与b共线时,n就不必然是平面α的法向量,故④错误.5.在长方体中,从同一极点动身的三条棱长别离为1,2,3,在以长方体的两个极点为起点和终点的向量中,模为1的向量有________个.[答案] 8[解析] 研究长方体模型可知,棱长为1的棱有4条,故模为1的向量有8个.三、解答题6.如图,正方体ABCD—EHGF,求出平面ABCD所有的法向量,并求出〈DA→,DC→〉、〈DA→,DF→〉.[分析] 依照法向量的概念求解,假设直线l垂直于平面ABCD,那么任何与直线l平行的非零向量都为法向量.[解析] 平面ABCD所有的法向量有DF→、CG→、BH→、AE→、FD→、GC→、HB→、EA→.由于正方体的三条棱DA、DC、DF相互垂直,因此〈DA→,DC→〉=90°,〈DA→,DF→〉=90°.一、选择题1.以下说法中正确的选项是( )A.任意两个空间向量都能够比较大小B.方向不同的空间向量不能比较大小,但同向的空间向量能够比较大小C.空间向量的大小与方向有关D.空间向量的模能够比较大小[答案] D[解析] 任意两个空间向量,不论同向仍是不同向均不存在大小关系,故A、B不正确;向量的大小只与其长度有关,与方向没有关系,故C不正确;由于向量的模是一个实数,故能够比较大小.2.在棱长为1的正方体ABCD—A1B1C1D1中,M和N别离为A1B1和BB1的中点,那么与直线AM垂直的向量有( )A.CN→B.BC→C.CC1→D.B1C1[答案] D[解析] 由于所求的是向量,因此第一排除B ,在剩下的三个选项中,通过正方体的图形可知D 项正确.3.已知正方形ABCD 的边长为4,GC ⊥平面ABCD ,且GC =2,那么向量AG →的模为( )A .6B .9C .4 2D .5[答案] A[解析] GC ⊥平面ABCD ,因此GC ⊥AC .在Rt △GAC 中,AC =42,GC =2,因此AG =AC 2+GC 2=6,即|AG →|=6.4.如下图,正方体ABCD —A 1B 1C 1D 1中,以极点为向量端点的所有向量中,直线AB 的方向向量有( )A .8个B .7个C .6个D .5个 [答案] A[解析] 与向量AB →平行的向量确实是直线AB 的方向向量,有AB →,BA →,A 1B 1→,B 1A 1→,C 1D 1→,D 1C 1→,CD →,DC →,共8个,因此选A.[点评] 直线的方向向量确实是与直线平行的非零向量,对模没有限制,注意起点和终点都在直线上的向量也是符合题意的.5.AB →=CD →的一个必要不充分条件是( )A .A 与C 重合B .A 与C 重合,B 与D 重合C .|AB →|=|CD →|D .A ,B ,C ,D 四点共线[答案] C[解析] 向量相等只需方向相同,长度相等,而与表示向量的有向线段的起点、终点的位置无关.表示两个共线向量的两条有向线段所在的直线平行或重合,不能取得四点共线.二、填空题6.在以下命题中:①若a 、b 为共面向量,那么a 、b 所在的直线平行;②假设向量a 、b 所在直线是异面直线,那么a 、b 必然不共面;③平面的法向量不唯一,但它们都是平行的;④平行于一个平面的向量垂直于那个平面的法向量.其中正确命题的个数为________.[答案] 2[解析] ①②是错误的,共面向量所在的直线不必然平行,只要能平移到一个平面内就能够够.7.如图,在正四棱台ABCD —A 1B 1C 1D 1中,O 、O 1别离是对角线AC ,A 1C 1的中点,那么〈AO →,OC →〉=________,〈AO →,O 1C 1→〉=________,〈OO 1→,A 1B 1→〉=________.[答案] 0° 0° 90°[解析] 由题意得AO →,OC →方向相同,是在同一条直线AC 上,故〈AO →,OC →〉=0°;O 1C 1→可平移到直线AC 上,与OC →重合,故〈AO →,O 1C 1→〉=0°;由题意知OO 1是正四棱台ABCD —A 1B 1C 1D 1的高,故OO 1⊥平面A 1B 1C 1D 1,因此OO 1⊥A 1B 1,故〈OO 1,A 1B 1→〉=90°.三、解答题8.一飞机从地面以45°倾角斜着升空,再水平向东飞行一段距离后,然后又水平向正北方向飞行,如此三次移动AB →、BC →、CD →是三个空间向量.问:(1)三个向量哪个与水平面平行?(2)〈AB →,BC →〉、〈BC →,CD →〉和〈AB →,CD →〉的值是多少?[分析] 应把实际问题抽象为数学问题,飞机水平飞行时与水平面平行,由图可知向量AB →与BC →在同一平面内,而且向量CD →垂直于那个平面α.[解析] (1)飞机水平飞行时所通过的线路与水平面平行,因此三个向量中BC →和CD →平行于水平面α.(2)由于向量AB →与BC →在同一平面内,设为平面β,又由于CD →为正北方向,因此CD →垂直于平面β,即BC →⊥CD→和AB →⊥CD →.因为AB →与水平面的夹角为45°,因此得:〈AB →,BC →〉=45°,〈BC →,CD →〉=90°,〈AB →,CD →〉=90°.9.如下图,正四棱锥P —ABCD 的底面边长为1.(1)试判定向量AB →,BC →,AD →,CD →中哪个是单位向量;(2)举出与向量AB →相等的向量.[解析] (1)单位向量即模为1的向量,那么AB →,BC →,AD →,CD →都是单位向量.(2)由于向量DC →与向量AB →方向相同,且模都为1,故DC →是与向量AB →相等的向量.10.如图,已知正方体ABCD —A 1B 1C 1D 1中,E 是A 1B 1的中点,F 是D 1B 1的中点.(1)问:向量AA 1→、CC 1→、DF →是不是为共面向量?(2)求〈BE →,BC →〉;(3)写出平面BB 1C 1C 的一个法向量.[解析] (1)向量DF →在平面D 1B 1BD 上,由于向量AA 1→、CC 1→平行于平面D 1B 1BD ,因此向量AA 1→、CC 1→、DF →都能够平移到平面D 1B 1BD 上,即向量AA 1→、CC 1→、DF →是共面向量.(2)在正方体ABCD —A 1B 1C 1D 1中,BC →为平面A 1B 1BA 的法向量,BE →又在平面A 1B 1BA 上,因此BC →⊥BE →,即〈BE →,BC →〉=90°.(3)平面BB 1C 1C 的一个法向量为BA →(或B 1A 1→、CD →、C 1D 1→).。