下载文档原格式
数控机床液体静压导轨结构的优化设计摘要：数控机床的导轨性能对数控机床的加工中心有着直接的影响，常规材料制造的机床导轨产生的动力学与热力学无法满足现代的高精度零件加工，为了提高数控机床的加工精准度，采用液体静压导轨并对导轨进行了改进。
本文以某型号数控机床加工中心的液体静压导轨为研究对象，并对液体静压导轨进行了改进，通过合理的数据假设进行设计，从而增加数控机床加工的精准性。
首先强化液体静态导轨的内部结构，其次对数控机床液体静压导轨的性能进行分析，最后针对液体静压导轨表面进行设计，将U-V形沟槽与V形沟槽进行减阻对比。
实验模拟结果表明：液体静压导轨的静压变形最大值较小，导轨油垫进行了完善设计；U-V形沟槽在减阻上面有着显著的效果，可以有效地改善液体静压的综合性能，并对数控机床的导轨设计提供参考意见。
关键词：数控机床；液体静压导轨；结构设计引文：随着现代化发展越来越快，人们对生活和工作的现代化产品要求越来越便利，导致现在产品的做工需要更加精密，因此各行各业对精密数据机床的需求更加地迫切。
在这样的大环境下，我国科研人员研究出了具有独立产权的精密数控机床，并以此为基础进行了改进和完善，本文以液体静态导轨作为研究对象，通过对导轨的改进提高切削功能与刀具的寿命，并在导体表面进行了合理的设计和完善，采用对比手段进行对照，得出最佳的液体静态导轨设计方案，从而提高数控机床中心加工技术的精准性，为推进现代化科技发展奠定基础[1]。
1液体静压导轨的分析与结构设计1.1液体静压导轨分析液体静压导轨是一种卧式加工中心，其导轨表面能有效地减阻。
图1显示了卧式加工中心的结构图。
在机床加工时，采用液体静压导轨对立柱进行支撑、固定和引导，以减少立柱和床身之间的摩擦，从而传导刀具与工件的作用力，使数控机床加工更加的精准[2]。
图1 卧式加工中心结构示意图例如，在一个经典的车床加工过程中，其主要的加工程序中：切削量f=0.5mm/r，则切削速度 vc=150 m/min，其它的参数都是通过参考相关的设计手册得到的。
液体静压导轨油膜厚度的控制及理论分析液体静压导轨的油膜厚度对导轨的性能有着重要的影响，为了保证在不同载荷条件下，液体静压导轨具有良好的运动精度和低速平稳性，利用矢量变频调速技术将油膜厚度始终控制在最优值。
在保证控制精度的前提下，降低系统成本，提高系统的可维护性和节能效果。
标签：液体静压导轨;油膜厚度控制;矢量变频调速0 前言液体静压导轨因其摩擦系数小，在起动和停止时没有磨损，精度保持性好等优点，目前被广范应用于航空航天设备、动力机械、军用装备及核工业中，特别是在精密和超精密机床中的应用尤为突出，其性能直接影响机床的加工性能。
液体静压导轨所用的工作介质为液压油，具有黏度大，阻尼特性好等特点，同时，液体静压导轨能够获得较大的刚度和承载能力，其抗振性要明显优于气体静压导轨。
在使用中，静压导轨与动压导轨和滚动导轨相比，需要一套复杂的专用液压设备，其维修、调整较为复杂，使用维护成本较高。
液体静压导轨通常在动导轨面上均匀分布有若干个油腔，通过外部供油系统将具有一定流量的压力油送入相对运动的导轨及油腔里，形成具有压力的油膜层，以此平衡外载荷，同时将动导轨微微抬起，与支撑导轨脱离接触，浮在压力油膜上，而这层油膜一般被称为静压油膜。
静压油膜很薄，其厚度仅在丝级或微米級上，在液体静压导轨中起着吸振减振及误差均化的作用，影响液体静压导轨的运动可靠性和运动精度，同时导轨的油膜厚度又决定了液体静压导轨的两个主要性能指标，导轨承载能力和油膜刚度[1]。
本文以定量供油开式静压导轨为例，从三个方面讨论分析了油膜厚度对导轨性能的影响，并通过矢量变频调速技术对油膜厚度进行控制，使油膜厚度始终处于最优值，为后期油膜厚度的进一步优化提供了理论依据。
1 液体静压导轨工作原理液体静压导轨按照不同的分类方式可分为以下四种：定压供油开式静压导轨、定量供油开式静压导轨、定压供油闭式静压导轨和定量供油闭式静压导轨。
图1为定量供油开式静压导轨工作原理图。
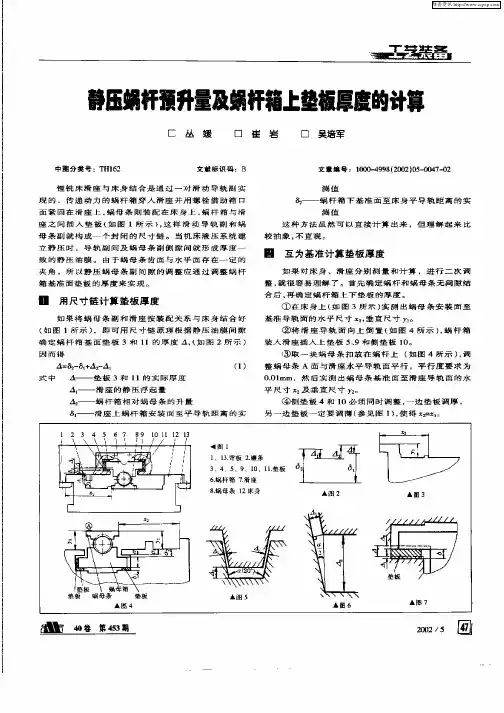
蜗杆各部分尺寸计算公式点加工导程＝6．3×3．1416＝19．79mm 模数*派蜗轮、蜗杆的计算公式：1，传动比=蜗轮齿数÷蜗杆头数2，中心距=（蜗轮节径+蜗杆节径）÷23，蜗轮吼径=（齿数+2）×模数4，蜗轮节径=模数×齿数5，蜗杆节径=蜗杆外径-2×模数6，蜗杆导程=π×模数×头数7，螺旋角（导程角）tgB=（模数×头数）÷蜗杆节径蜗杆导程=π×模数×头数模数=分度圆直径/齿数头数是说螺杆上螺旋线的条数；模数是指螺杆上螺旋线的大小，也就是模数越大螺杆上的螺旋线就越“柱装”（东北话，就是比较大，比较结实）直径系数是指螺杆的粗细。
模数:齿轮的分度圆是设计、计算齿轮各部分尺寸的基准,而齿轮分度圆的周长=πd=z p,于是得分度圆的直径d=z p/π由于在上式中π为一无理数,不便于作为基准的分度圆的定位.为了便于计算,制造和检验,现将比值p/π人为地规定为一些简单的数值,并把这个比值叫做模数(module),以m表示,即令其单位为mm.于是得:模数m是决定齿轮尺寸的一个基本参数.齿数相同的齿轮模数大,则其尺寸也大.为了便于制造,检验和互换使用,齿轮的模数值已经标准化了.建筑模数建筑模数指建筑设计中选定的标准尺寸单位。
它是建筑设计、建筑施工、建筑材料与制品、建筑设备、建筑组合件等各部门进行尺度协调的基础。
就象随便来个尺寸,建筑构件就无法标准化了，难统一。
基本模数的数值规定为100mm，以M表示，即1M= 100mm。
导出模数分为扩大模数和分模数,扩大模数的基数为3M，6M，12M，15M，30M，60M共6个;分模数的基数为1/10M，1/5M，1/2M共3个.使用3M是《中华人民共和国国家标准建筑统一模数制》中为了既能满足适用要求，又能减少构配件规格类型而规定的。
蜗杆蜗轮传动设计计算.txt蜗杆蜗轮传动设计计算一、简介蜗杆蜗轮传动是一种常见的传动方式，常用于机械设备中。
本文将介绍蜗杆蜗轮传动的设计计算方法。
二、设计计算1. 轴心距计算：蜗杆蜗轮传动中，轴心距的确定直接影响到传动性能。
一般可根据设备要求和材料选择来确定轴心距的大小。
2. 蜗杆蜗轮参数计算：- 蜗杆参数计算：蜗杆的参数包括蜗杆齿轮模数、齿数、蜗杆导程等。
根据蜗杆传动的工作要求，可通过相关公式计算得到蜗杆的参数。
- 蜗轮参数计算：蜗轮的参数包括蜗轮齿数、齿轮模数等。
蜗轮参数的确定需要考虑到蜗杆蜗轮传动的匹配性，一般可通过公式计算得到蜗轮的参数。
3. 力学计算：- 扭矩计算：根据传动功率和旋转速度，可以计算传动中所需的扭矩。
- 轴强度计算：蜗杆蜗轮传动的轴强度是设计中需要考虑的重要因素之一。
根据传动扭矩、材料强度等参数，可以进行轴强度的计算。
4. 效率计算：蜗杆蜗轮传动的效率影响着传动的能量损失。
通过相关公式和参数，可以计算蜗杆蜗轮传动的效率。
三、注意事项在进行蜗杆蜗轮传动设计计算时，需要注意以下几点：1. 使用合理的参数值和公式，确保计算结果准确可靠。
2. 考虑到材料的强度和耐磨性等因素，在选择蜗杆和蜗轮的材料时要谨慎。
3. 需要根据实际情况对设计参数进行适当调整，以满足工作要求和设备性能。
四、总结蜗杆蜗轮传动设计计算是机械设备设计中的重要内容，通过合理的设计计算能够确保传动的准确性和可靠性。
要注意选择合适的参数和材料，并根据实际情况对设计参数进行调整。
以上为蜗杆蜗轮传动设计计算的简要介绍，希望对您有所帮助。
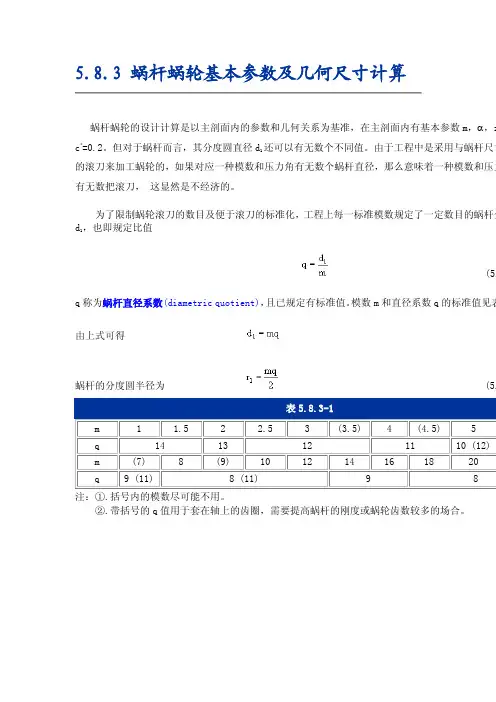
5.8.3 蜗杆蜗轮基本参数及几何尺寸计算
蜗杆蜗轮的设计计算是以主剖面内的参数和几何关系为基准，在主剖面内有基本参数m，α，z
还可以有无数个不同值。
由于工程中是采用与蜗杆尺寸c*=0.2。
但对于蜗杆而言，其分度圆直径d
1
的滚刀来加工蜗轮的，如果对应一种模数和压力角有无数个蜗杆直径，那么意味着一种模数和压力有无数把滚刀，这显然是不经济的。
为了限制蜗轮滚刀的数目及便于滚刀的标准化，工程上每一标准模数规定了一定数目的蜗杆分，也即规定比值
d
1
(5. q称为蜗杆直径系数(diametric quotient)，且已规定有标准值。
模数m和直径系数q的标准值见表
由上式可得
蜗杆的分度圆半径为 (5.
注：①.括号内的模数尽可能不用。
②.带括号的q值用于套在轴上的齿圈，需要提高蜗杆的刚度或蜗轮齿数较多的场合。
图5.8.3-1
如图5.8.3-1所示，蜗杆螺度圆柱面的交线为螺旋线，设有两条螺旋线。
将分度圆柱展则螺旋线展成斜直线。
图中与λ有关的参数有：H ──导程，且H=z
1
P
a1
P
a1
──轴面齿距，即 P
a1
=πm 由图得
由此看出影响λ大小的因素有z
1
、q。
①.当q一定，蜗杆的齿数z
1
增多，螺旋线导程角λ增大；
②.当z
1一定，蜗杆的直径系数q增大（也即直径d
1
增大），螺旋线导程角λ减小。
螺旋线导程角λ的大小直接影响到蜗杆蜗轮传动的自锁性，λ越小，机构越易自锁。
标准阿基米德蜗杆蜗轮机构的几何尺寸计算公式见表5.8.3-2。
稳健设计理论在液体动压滑动轴承中的应用滑动轴承是各种传动装置中广泛采用的支承件，特别是在高速运转机械中，为了减小摩擦，提高传动效率，要求轴承与轴颈间脱离接触并具有足够的油膜厚度，以形成液体间的摩擦状态。
在滑动轴承设计中，只有当轴承尺寸、轴承载荷、相对运动速度、润滑油的粘度、轴承间隙以及表面粗糙度之间满足一定关系时，才能实现液体摩擦。
任一参数取值不当，将出现非液体摩擦状态，导致液体摩擦的失效。
以上参数的优化设计对轴承的使用性能及寿命有十分重要的作用。
通常，在设计中，往往对轴承的各设计参数和使用条件提出更高要求。
轴承的设计参数或误差对轴承的性能的影响是非线性的，在不同的设计方案中，同样的误差程度，所产生的性能波动不尽相同。
稳健设计就是找到一种设计方案，使得液体动压轴承的性能对误差不十分敏感，同时达到较宽松的加工经济精度而降低成本的目的。
本文对某液体动压滑动轴承进行稳健设计，建立相应的数学模型，并求得优化的设计方案。
1滑动轴承的工程分析下面是径向动压滑动轴承的一组计算公式。
1.最小油膜厚度h minh min=C-e=C(1－ε)=rψ(1－ε)（1）式中C=R－r——半径间隙，R轴承孔半径；r轴颈半径；ε=e/C——偏心率；e为偏心距；ψ=C/r——相对间隙，常取ψ=(0.6-1)×10-3(v)1/4，v 为轴颈表面的线速（m/s ）设计时，最小油膜厚度h min 必须满足：h min /(R z1+R z2)≥2-3［1］(2)式中R z1、R z2为轴颈和轴承的表面粗糙度。
2.轴承的特性系数（索氏系数）S=μn ／（p ψ2）（3）式中μ——润滑油在轴承平均工作温度下的动力粘度（Pa ·s ）；n ——轴颈的转速（r/s ）；p ——平均压强（N/m 2）用来检验轴承能否实现液体润滑。
ε值可按下面简化式求解。
A ε2+E ε+C=0（4）其中A=2.31(B/d)-2,E=－(2.052A ＋1),C=1＋1.052A －6.4088S.上式中d ——轴径的直径（m ）；B ——轴承的宽度（m ）通常ε选在0.5-0.95之间，超出0-1间的值，均非ε的解［1］。
7 蜗轮蜗杆的设计及其参数计算5.1 传动参数蜗杆输入功率P=5.3 kW ，蜗杆转速min /r 960n 1=，蜗轮转速m i n /r 5.56n 2=，理论传动比i=16.75，实际传动比i=17，蜗杆头数2Z 1=，蜗轮齿数为34217 Z i Z 12=⨯==，蜗轮转速min /r 5.5617960i n n 12=== 5.2 蜗轮蜗杆材料及强度计算减速器的为闭式传动，蜗杆选用材料45钢经表面淬火，齿面硬度 >45 HRC,蜗轮缘选用材料ZCuSn10Pb1,砂型铸造。
蜗轮材料的许用接触应力，由《机械设计基础》表4-5可知,[]H σ=180MPa. 估取啮合效率： 10.8η= 蜗轮轴转矩：6651122 5.250.89.55109.55107.110mm n 56.5P T N η⨯=⨯=⨯⨯=⨯⋅ 载荷系数：载荷平稳，蜗轮转速不高，取K=1.1.计算21m d 值 []22122480m d HKT Z σ⎛⎫≥⎪ ⎪⎝⎭=2534801.17.110mm 34180⎛⎫⨯⨯⨯ ⎪⨯⎝⎭=34804mm模数及蜗杆分度圆直径由《机械设计基础》表4-1取标准值，分别为： 模数 m=8 mm蜗杆分度圆直径 1d 80m m = 5.3 计算相对滑动速度与传动效率蜗杆导程角11mz 82=arctanarctan 11.31d 80γ⨯==蜗杆分度圆的圆周速度111d n 80960m /s 4.02m /s 601000601000ππυ⨯⨯===⨯⨯相对活动速度1s 4.024.098m/s cos cos11.31υυγ===当量摩擦角 取v 230 2.5ρ== 验算啮合效率()()1v tan tan11.31081tan tan 11.31 2.5γηγρ===++（与初取值相近）。
传动总效率10.960.960.810.78ηη==⨯=总 （在表4-4所列范围内）。
5.8.3 蜗杆蜗轮基本参数及几何尺寸计算蜗杆蜗轮的设计计算是以主剖面内的参数和几何关系为基准，在主剖面内有基本参数m，α，z2，=1，c*=0.2。
但对于蜗杆而言，其分度圆直径d1还可以有无数个不同值。
由于工程中是采用与蜗杆尺寸基本相同的滚刀来加工蜗轮的，如果对应一种模数和压力角有无数个蜗杆直径，那么意味着一种模数和压力角就得备有无数把滚刀，这显然是不经济的。
为了限制蜗轮滚刀的数目及便于滚刀的标准化，工程上每一标准模数规定了一定数目的蜗杆分度圆直径d1，也即规定比值(5.8.3-1)q称为蜗杆直径系数(diametric quotient)，且已规定有标准值。
模数m和直径系数q的标准值见表5.8.3-1。
由上式可得蜗杆的分度圆半径为 (5.8.3-2)注：①.括号内的模数尽可能不用。
②.带括号的q值用于套在轴上的齿圈，需要提高蜗杆的刚度或蜗轮齿数较多的场合。
图5.8.3-1如图5.8.3-1所示，蜗杆螺旋面与分度圆柱面的交线为螺旋线，设z1=2，则有两条螺旋线。
将分度圆柱展成平面，则螺旋线展成斜直线。
图中与λ有关的参数有：H ──导程，且H=z1P a1P a1──轴面齿距，即 P a1=πm由图得由此看出影响λ大小的因素有z1、q。
①.当q一定，蜗杆的齿数z1增多，螺旋线导程角λ增大；②.当z1一定，蜗杆的直径系数q增大（也即直径d1增大），螺旋线导程角λ减小。
螺旋线导程角λ的大小直接影响到蜗杆蜗轮传动的自锁性，λ越小，机构越易自锁。
标准阿基米德蜗杆蜗轮机构的几何尺寸计算公式见表5.8.3-2。
残阳渐逝，血红冲天。
半是夕阳余光，半是狰狞血雨。
是的，血，到处都是冷腥的鲜血。
整个皇宫之内，血流成河，白玉理石全被洗涮成黑红之色，到处是断壁残肢，尸横一片，到处是厮杀后的痕迹。
“为什么？”百里冰左手紧捂着胸口，瞪大着眼睛看着对面十米敌对方处，挥手点兵之人。
那是她的未婚夫，她倾尽一生所爱之人。
亦是绝杀她百里一族，将她迫入绝境之人。
§13—5液体动力润滑径向滑动轴承的设计计算一、动压油膜和液体摩擦状态的建立过程流体动力润滑的工作过程：起动、不稳定运转、稳定运转三个阶段起始时n=0，轴颈与轴承孔在最下方位置接触1、起动时，由于速度低，轴颈与孔壁金属直接接触，在摩擦力作用下，轴颈沿孔内壁向右上方爬开。
2、不稳定运转阶段，随转速上升，进入油楔腔内油逐渐增多，形成压力油膜，把轴颈浮起推向左下方。
（由图b→图c）3、稳定运转阶段（图d）：油压与外载F平衡时，轴颈部稳定在某一位置上运转。
转速越高，轴颈中心稳定位置愈靠近轴孔中心。
（但当两心重合时，油楔消失，失去承载能力）从上述分析可以得出动压轴承形成动压油膜的必要条件是（1）相对运动两表面必须形成一个收敛楔形（2）被油膜分开的两表面必须有一定的相对滑动速度v s，其运动方向必须使润滑从大口流进，小口流出。
（3）润滑油必须有一定的粘度，供油要充分。
v越大，η越大，油膜承载能力越高。
实际轴承的附加约束条件：压力pv值速度最小油膜厚度温升二、最小油膜厚度h min1、几何关系图13－13 径向滑动轴承的几何参数和油压分布O—轴颈中心，O1—轴承中心，起始位置F与OO1重合，轴颈半径-r，轴承孔半径R∴半径间隙：（13-6-1）半径间隙：（13-6）相对间隙：（13-7）偏心距：（13-8）偏心率：（13-9）以OO1为极轴，任意截面处相对于极轴位置为φ处对应油膜厚度为h，（13-10）h的推导：在中，根据余弦定律可得（13-11）略去高阶微量，再引入半径间隙，并两端开方得（13-12）三.流体动力润滑基本方程（雷诺方程）流体动力润滑基本方程（雷诺方程）是根据粘性流体动力学基本方程出发，作了一些假设条件后简化而得的。
假设条件是：1）忽略压力对润滑油粘度的影响；2）流体为粘性流体；3）流体不可压缩，并作层流；4）流体膜中压力沿膜厚方向是不变的；2）略去惯性力和重力的影响。
可以得出：∴（13-13）一维雷诺流体动力润滑方程上式对x取偏导数可得（13-14）若再考虑润滑油沿Z方向的流动，则（13-15）二维雷诺流体动力润滑方程式四、最小油膜厚度由中可看出油压的变化与润滑油的粘度、表面滑动速度和油膜厚度的变化有关，利用该式可求出油膜中各点的压力p，全部油膜压力之和即为油膜的承载能力。
