泄漏源及扩散模式
- 格式:doc
- 大小:199.00 KB
- 文档页数:17


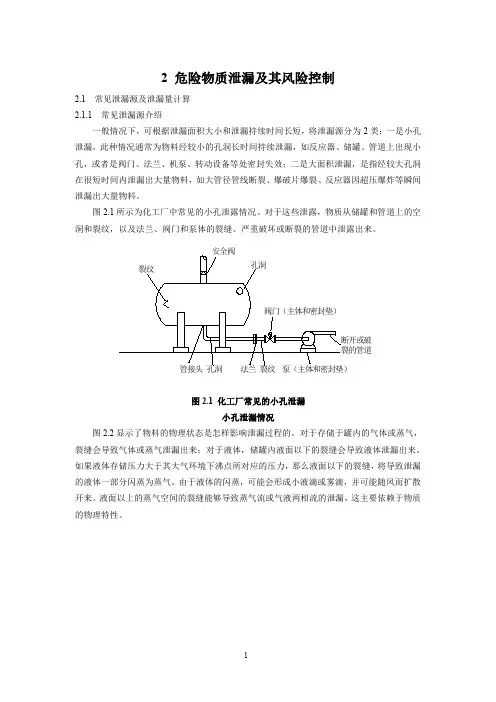



第六章泄漏源及扩散模式很多事故是由于物料的泄漏引起的。
因泄漏而导致事故的危害,很大程度上取决于有毒有害,易燃易爆物料的泄漏速度和泄漏量。
物料的物理状态在其泄漏至空气中后是否发生改变,对其危害范围也有非常明显的影响,泄漏物质的扩散不仅由其物态、性质所决定,又为当时气象条件、当地的地表情况所影响。
6.1常见泄漏源泄漏源分为两类:一是小孔泄漏:通常为物料经较小的孔洞,长时间持续泄漏。
如反应器、管道、阀门等出现小孔或密封失效;二是大面积泄漏:在短时间内,经较大的孔洞泄漏大量物料。
如管线断裂、爆破片爆裂等。
为了能够预测和估算发生泄漏时的泄漏速度、泄漏量、泄漏时间等,建立如下泄漏源模型,描述物质的泄漏过程:1.流体流动过程中液体经小孔泄漏的源模式;2.储罐中液体经小孔泄漏的源模式;3.液体经管道泄漏的源模式;4.气体或蒸汽经小孔泄漏的源模式;5.闪蒸液体的泄漏源模式;6.易挥发液体蒸发的源模式。
针对不同的工艺条件和泄漏源情况,应选用相应的泄漏源模式进行泄漏速度、泄漏量、泄漏时间的求取。
6.2 流体流动过程中液体经小孔泄漏的源模式系统与外界无热交换,流体流动的不同能量形式遵守如下的机械能守恒方程:(6—1)式中:P——压力,Pa;ρ——流体密度,kg/m3;α——动能校正因子,无因次;α≈1U ——流体平均速度,m/s;g ——重力加速度,g = 9.81 m/s2;z ——高度,m;F ——阻力损失,J/kg;W s ——轴功率,J;m ——质量,kg。
对于不可压缩流体,密度ρ恒为常数,有:(6—2)泄漏过程暂不考虑轴功率,W s =0,则有:(6—3)液体在稳定的压力作用下,经薄壁小孔泄漏,如图6.1所示。
容器内的压力为p1,小孔直径为d,面积为A,容器外为大气压力。
此种情况,容器内液体流速可以忽略,不考虑摩擦损失和液位变化,可得到:式中,Q为单位时间内流体流过任一截面的质量,称为质量流量,其单位为kg/s。




放射性气体扩散的预估模型摘要:由于放射性气体泄漏造成惨重损失的报道在国际屡见不鲜,近日日本福岛核电站的放射性气体的泄漏事件更让我们关注放射性气体泄漏时在环境中的浓度问题,为了今后事故发生后提供积极的补救措施, 所以对放射性气体的扩散作深入的研究是很有必要的。
本文结合高斯烟羽模型、线性拟合,以及微分方程模型,运用MA TLAB软件,分析了泄漏源强度、风速、大气稳定度参数、地面粗糙度参数和计算精确度等的因素对放射性气体扩散的影响,预测了放射性气体浓度在不同时间,不同地区的浓度变化,并且本文模型中的数据可以根据不同的实际情况而加以改变,因而使本文的应用范围大大增加,可以适用于具有较强的应用性。
文章首先在第一问中利用MA TLAB软件对数据进行线性拟合,采用微分方程模型得到核电站周边放射性气体在不同地区,不同时间段的浓度变化,得出随着离泄漏源距离的延伸,最终放射性物质的浓度越来越小,趋近于零,即当L趋向无穷是,C(x,y,z,t)趋向于零;当时间趋于无穷时,C(x,y,z,t)也趋于无穷。
问题二,问题三中,建立以核电站周边不同地区得距离以及风速为因变量,设置各个主要因素的参考数据,同时,利用高斯烟羽模型对核电站周边地区的浓度进行预测,然后,利用MATLAB软件,将相关数据代入程序,我们得到核电站周边地区的浓度分布的等高曲线。
问题四中,通过实际收集数据,集合核电站周边地区的浓度等高曲线,可以直观的看出日本福岛核电站对我国东海岸以及美国西海岸的影响。
一.问题的提出1.1背景的介绍目前,核电的发展给国家带来了巨大的经济效益和社会效益,但核电正常运行以及发生泄露时不可避免的会有气载放射性核素排出,这样就给周围的环境产生了一定的影响,因此,正确的测出大气中放射性物质的浓度在环境检测以及安全评估中具有重要意义。
1.2需要解决的问题的放射性气体以匀速排出,设有一座核电站遇自然灾害发生泄漏,浓度为p速度为m kg/s,在无风的情况下,匀速在大气中向四周扩散, 速度为s m/s.(1)请你建立一个描述核电站周边不同距离地区、不同时段放射性物质浓度的预测模型。
第六章泄漏源及扩散模式很多事故是由于物料的泄漏引起的。
因泄漏而导致事故的危害,很大程度上取决于有毒有害,易燃易爆物料的泄漏速度和泄漏量。
物料的物理状态在其泄漏至空气中后是否发生改变,对其危害范围也有非常明显的影响,泄漏物质的扩散不仅由其物态、性质所决定,又为当时气象条件、当地的地表情况所影响。
6.1常见泄漏源泄漏源分为两类:一是小孔泄漏:通常为物料经较小的孔洞,长时间持续泄漏。
如反应器、管道、阀门等出现小孔或密封失效;二是大面积泄漏:在短时间内,经较大的孔洞泄漏大量物料。
如管线断裂、爆破片爆裂等。
为了能够预测和估算发生泄漏时的泄漏速度、泄漏量、泄漏时间等,建立如下泄漏源模型,描述物质的泄漏过程:1.流体流动过程中液体经小孔泄漏的源模式;2.储罐中液体经小孔泄漏的源模式;3.液体经管道泄漏的源模式;4.气体或蒸汽经小孔泄漏的源模式;5.闪蒸液体的泄漏源模式;6.易挥发液体蒸发的源模式。
针对不同的工艺条件和泄漏源情况,应选用相应的泄漏源模式进行泄漏速度、泄漏量、泄漏时间的求取。
6.2 流体流动过程中液体经小孔泄漏的源模式系统与外界无热交换,流体流动的不同能量形式遵守如下的机械能守恒方程:(6—1)式中:P——压力,Pa;ρ——流体密度,kg/m3;α——动能校正因子,无因次;α≈1U ——流体平均速度,m/s;g ——重力加速度,g = 9.81 m/s2;z ——高度,m;F ——阻力损失,J/kg;W s ——轴功率,J;m ——质量,kg。
对于不可压缩流体,密度ρ恒为常数,有:(6—2)泄漏过程暂不考虑轴功率,W s =0,则有:(6—3)液体在稳定的压力作用下,经薄壁小孔泄漏,如图6.1所示。
容器内的压力为p1,小孔直径为d,面积为A,容器外为大气压力。
此种情况,容器内液体流速可以忽略,不考虑摩擦损失和液位变化,可得到:式中,Q为单位时间内流体流过任一截面的质量,称为质量流量,其单位为kg/s。
考虑到因惯性引起的截面收缩以及摩擦引起的速度减低,引入孔流系数C0,则经小孔泄漏的实际质量流量为:kg /s(6—7)式中:Q——质量流量,kg / s;A——泄漏孔面积,m2;C0——孔流系数;p1——容器内的压力,Pa;ρ——流体密度,kg / m3。
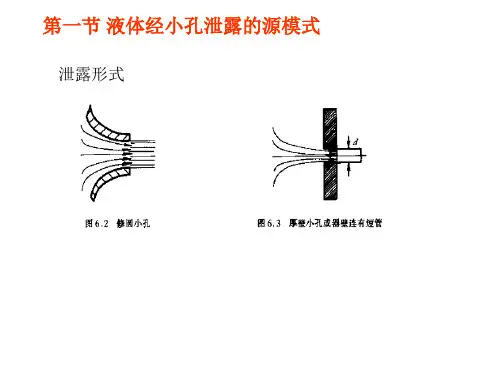
C0的取值:1、薄壁小孔( 壁厚≤d / 2 ),Re > 105C0 = 0.612、厚壁小孔( d / 2 < 壁厚≤4d ),或在孔处伸有一段短管(见图6.3 ) C0 = 0.813、修圆小孔( 见图6.2 ) C0 = 1但在很多情况下难以确定泄漏孔口的孔流系数,为了保证安全裕量,确保估算出最大的泄漏量和泄漏速度,Co值可取为1。
例:某液体在容器中以稳定的0.2MPa的压力完全湍流流动,液体的密度为1000kg / m3,因时久腐蚀的原因,容器底部有一小孔发生泄漏,孔径为5mm,壁厚≤d/2,孔流系数C0 = 0.62,容器外部为大气压;问经小孔泄漏的实际质量流量为多少?解:按液体经小孔的泄漏源模式(6—7)计算:Q = AC0(2 p1ρ)1/2= 0.7854×0.0052×0.62(2×0.2×106×1000)= 0.24 kg / s6.3 储罐中液体经小孔泄漏的源模式如图6.4所示的液体储罐,距液体位高度Z0处有一小孔,在静压能和势能的作用下,液体经小孔向外泄漏,泄漏过程可由机械能守恒方程描述,罐内液体流速忽略,罐内液体压力为P g,外部为大气压(表压P=0),如前面定义孔流系数C0,由下式表达:(6—8)将式(6—8)代入式(6—3)中,可求泄漏速度U:(6—9)小孔截面积为A,则质量流量Q为:(6—10)但是储罐内液位高度z0不断下降,泄漏速度和质量流量也随之减少,假定储罐与大气相通,则内外压差Δp为0,则上式简化为:(6—11)若储罐的横截面积为A0,则经小孔泄漏的最大液体量m为:(6—12)取一微元时间内液体的泄漏量:(6—13)并且罐内液体质量的变化速率,即为泄漏质量:(6—14)将式(6—11)、(6—13)代入(6—14)式,得到:(6—15)设定边界条件:t=0,t=t,z=z0 ,z=z,对上式进行积分,有:(6—16)当液体泄漏到泄漏点位置时,泄漏停止,z=0,为此,得到总的泄漏时间:(6—17)将式(6—16)代入式(6—11)中得到随时间变化的质量流量关系:(6—18)式中:ρ——流体密度,kg / m3;C0——孔流系数;A ——泄漏孔面积,m2;A0——储罐截面积,m2;z0 ——泄漏点以上液体的高度,m;g ——重力加速度,9.81m / s2;t ——泄漏时间,s。
如果储罐内盛装的是易燃液体,为防止可燃蒸汽大量泄漏至空气中,或空气大量进入储罐内的气相空间,形成爆炸性混合物,通常情况下会采取通氮气保护的措施。
液体表压为P g,外部为大气压(表压P=0),内外压差即为P g,则根据式(6—10)、式(6—12)、式(6—13)、式(6—14)可同理得到:将式(6—20)代入式(6—10)得到任意时刻的质量流量Q:式中:P g——储罐内液体表压,Pa。
根据上式(6—21)可求出不同时间的泄漏质量流量。
例:有一常压甲苯储罐,内径1 m,下部因腐蚀产生一个小孔,孔直径为10mm,小孔上方甲苯液位初始高度为3 m,巡检人员于上午7:00发现泄漏,马上进行堵漏处理,完工后,小孔上方液位高度1.8 m,请计算已泄漏掉甲苯的量kg和泄漏始于何时?已知甲苯的密度ρ =900 kg / m3, C0=1。
解:(1)求泄漏质量流量随时间的变化式C0 = 1Q =ρC0A(2gz0)1/2-(ρgC02A2/A0) tz0 = 3m ρ= 900kg/m3g = 9.81A = 0.012×π/4 = 7.854×10-5 m2A0 = 12×π/4 = 0.7854 m2将有关数据代入计算:Q = 900×1×7.854×10-5 (2×9.81×3)1/2-[900×9.81×12×(7.854×10-5)2/0.7854] t整理后得:Q = 0.5423-0.00006934t(2)求任一时间内总的泄漏量W为泄漏质量流量对时间的积分:W =∫0t Qdt =∫0t (0.5423-0.00006934t) dt而W =π/4×D2z1ρ=π/4×12×(3-1.8)×900 = 848.23 kg所以848.23 = ∫0t (0.5423-0.00006934t) dt积分后得:848.23 = 0.5423t-0.00003467t2(a)式(a)为一元二次方程:0.00003467t2-0.5423t + 848.23 = 0求解:根据t =[-b±(b2-4ac)1/2] / 2aa = 0.00003467b =-0.5423c = 848.23t = 0.5423±(0.54232-4×0.00003467×848.23)1/2 /(2×0.00003467)解得:t1 = 13878 s t2 = 1764 s用t1代入(a)式不符,舍去,取t2 = 1764 s (也就是说泄漏掉848.23kg甲苯用时1764秒)1764 / 60 = 29.4 min(3)已知早上7:00发现泄漏并即时堵漏,则泄漏约始于早上6:31分左右,总泄漏掉的甲苯为848.23 kg。
6.4 液体经管道泄漏的源模式化工生产中,通常采用圆形管道输送流体。
如果管道发生爆裂、折断等,可造成液体经管口泄漏,其泄漏过程可用来描述。
其中阻力损失F的计算是估算泄漏速度和泄漏量的关键。
流动阻力分为直管阻力和局部阻力:1、直管阻力F1的计算:(范宁公式) (6—22)式中:λ——摩擦系数,无因次;l——管长,m;d ——管径,m;U ——流速,m/s。
λ的计算与Re数有关,Re≤2000时,属层流,λ=64/Re2000≤Re≤4000时,属过渡流,λ=0.0025Re1/3Re>4000时,属湍流,λ=f ( Re,ε/ d ),ε/d称相对粗糙度,ε为管壁粗糙度,d 为圆管内径。
ε值可由表6.1查得。
对于光滑管:以上是采用一些公式对λ值进行计算,λ也可根据Re和ε/d,查图6.7查得λ值,此图也称莫迪图。
图6.7 莫迪图上图按雷诺准数范围可分为如下四个区域:a、滞流区(Re≤2000),λ=64/Re,与ε/d无关,λ和Re准数成直线关系。
b、过渡区(2000<Re<4000),流动处于不稳定状态,在此区域内滞流或湍流的λ~Re 曲线都可应用。
为安全起见,对于流动阻力的计算,一般将湍流时的曲线延伸,以查取λ值。
c、湍流区(Re≥4000及虚线以下的区域), λ与Re和ε/d均有关,在这个区域内对于不同的ε/d标绘出一系列曲线;其中最下面的一条曲线为流体通过光滑管的摩擦系数λ与Re的关系曲线。
d、完全湍流区(在图中虚线以上的区域),λ与Re无关,仅与ε/d有关。
2、局部阻力F2的计算:可将局部阻力按当量长度或动能折合来计算。
按当量长度计算:(6—23)式中: le——当量长度,m。
按动能计算:(6—24)式中:ξ——局部阻力系数。
ξ值可由表6.2和表6.3查得。
3、总的阻力损失F的计算:总的阻力损失为直管阻力损失和局部阻力损失之和:F=F直管+F局部或F=λ(l/d)×(U2/2)+Σξ(U2/2)(6—25)将已知数据代入(6.3)式并整理(Z是减少,取“-”号):U2/2 +(-gZ)+1.78U1.75 +0.085U2 = 0U2/2 +1.78U1.75 +0.085U2 = 9.8×5将等式两边同乘以2,得:1.17U2+3.56U1.75 = 98再设定流速U的数值,代入上式,直到上等式两端相等:初设U = 5.6 m/s 等式左端为109.3, 等式右端为98,显然不符;重设U = 5.4 m/s 等式左端为102.2, 等式右端为98,显然不符;再设U = 5.3 m/s 等式左端为98.8, 等式右端为98,基本符合;误差:(98.8-98)/98×100 % = 0.8 % 已很小;计算结果显示Re = 5.3×105 在4000 <Re <106 内,说明U选择正确。
泄漏的最大质量流量Q为:Q = ΡUA = 1000×5.3×0.12×π/4 = 41.62 kg/s6.5 气体或蒸汽经小孔泄漏的源模式气体或蒸汽是可压缩气体,工程上通常将气体或蒸汽近似为理想气体,它们的压力、密度、温度等参数遵循理想气体状态方程。