对数等模拟运算电路

集成运算放大器基本应用 （模拟运算电路）实训指导（特别提醒：实验电路图中可能存在有的元器件数值与实验电路板中的不相同，实验时应以实验电路板中的为准。

另外，由于元器件老化、湿度变化、温度变化等诸多因素的影响所致，实验电路板中所标的元器件数值也可能与元器件的实际数值不一致。

有的元器件虽然已经坏了，但仅凭肉眼看不出来。

因此，在每次实验前，应该先对元器件（尤其是电阻、电容、三极管）进行单个元件的测量（注意避免与其它元器件或人体串联或并联在一块测量）。

并记下元器件的实际数值。

否则，实验测得的数值与计算出的数值可能无法进行科学分析。

）一．实验目的1．研究由集成运放组成的比例、加法、减法和积分等基本运算电路的功能。

2．了解运算放大器在实际应用时应考虑的一些问题。

二．实验原理集成运算放大器是一种具有高电压放大倍数的直接耦合多级放大电路。

当外部接入不同的线性或非线性元器件组成输入和负反馈电路时，可以灵活地实现各种特定的函数关系。

在线性应用方面，可组成比例、加法、减法、积分、微分、对数等模拟运算电路。

基本运算电路。

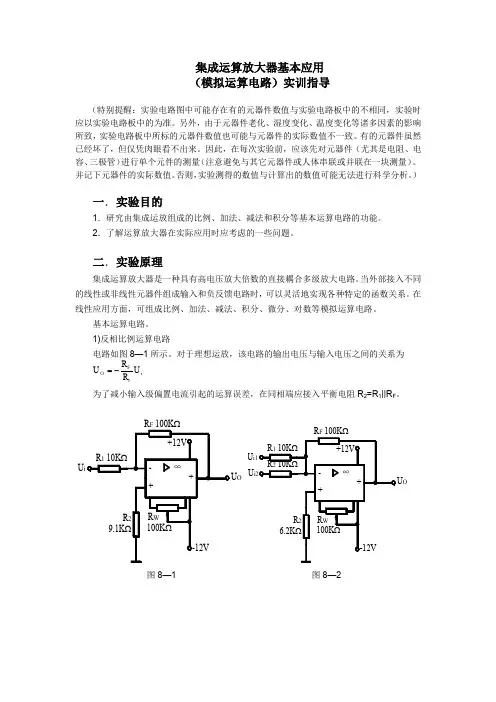
1)反相比例运算电路电路如图8—1所示。

对于理想运放，该电路的输出电压与输入电压之间的关系为i F O U R RU 1-=为了减小输入级偏置电流引起的运算误差，在同相端应接入平衡电阻R 2=R 1||R F 。

U OOU U图8—1 图8—22)反相加法电路电路如图8—2，输出电压与输入电压之间的关系为)(2211i F i F O U R RU R R U +-=R 3= R 1‖R 2‖R F 3)同相比例运算电路图8—3(a)是同相比例运算电路，它的输出电压与输入电压之间的关系为 i F O U R R U ⎪⎪⎭⎫ ⎝⎛+=11 R 2 = R 1‖R F当R 1 ∞，U o =U i ，即得到如图8—3(b)所示的电压跟随器，图中R 2=R F ，用以减小漂移和起保作用。

一般R F 取10K Ω，R F 太小起不到保护作用，太大则影响跟随性。

实验二 集成运算放大器的基本应用—— 模拟运算电路一、实验目的1、 研究由集成运算放大器组成的比例、加法、减法和积分等基本运算电路的功能。

2、 了解运算放大器在实际应用时应考虑的一些问题。

二、实验仪器1、 双踪示波器2、 万用表3、 交流毫伏表4、 信号发生器 三、电路理论回顾集成运算放大器在线性应用方面，可组成比例、加法、减法、积分、微分、对数、指数等模拟运算电路。

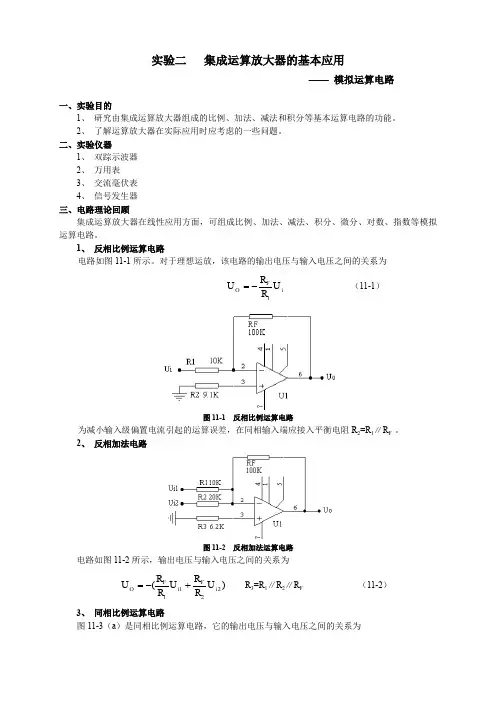
1、 反相比例运算电路电路如图11-1所示。

对于理想运放，该电路的输出电压与输入电压之间的关系为i FO U R R U 1-= （11-1）图11-1 反相比例运算电路为减小输入级偏置电流引起的运算误差，在同相输入端应接入平衡电阻R 2=R 1∥R F 。

2、 反相加法电路图11-2 反相加法运算电路电路如图11-2所示，输出电压与输入电压之间的关系为)(2211i F i F O U R RU R R U +-= R 3=R 1∥R 2∥R F （11-2） 3、 同相比例运算电路图11-3（a ）是同相比例运算电路，它的输出电压与输入电压之间的关系为i FO U R R U )1(1+= R 2=R 1∥R F （11-3） 当R1→∞时，U O =U i ，即得到如图11-3（b ）所示的电压跟随器。

图中R 2=R F ，用以减小漂移和起保护作用。

一般R F 取10K Ω，R F 太小起不到保护作用，太大则影响跟随性。

图11-3 同相比例运算电路4、 差动放大电路(减法器)对于图11-4所示的减法运算电路，当R1=R2，R3=RF 时，有如下关系式： )(1120i i U U R RFU -=（11-4）图11-4 减法运算电路5、 积分运算电路图11-5 积分运算电路反相积分电路如图11-5所示。

在理想化条件下，输出电压U 0等于 001()(0)ti C U t U dt U RC =-+⎰ （11-5） 式中U C (0)是t=0时刻电容C 两端的电压值，即初始值。

运算放大器在实际中的应用广西大学电气工程学院摘要：运算放大器是目前应用最广泛的一种器件,当外部接入不同的线性或非线性元器件组成输入和负反馈电路时，可以灵活地实现各种特定的函数关系。

在线性应用方面，可组成比例、加法、减法、积分、微分、对数等模拟运算电路。

关键词：结构组成，工作原理，基本原理电路,实际应用The application of Operational amplifier in practice Abstract：Operational amplifier is one of the most widely used devices, when external access different linear or nonlinear components of input and negative feedback circuit, can flexibly implement specific function. In the aspects of linear composition proportion, addition, subtraction, integral, differential, logarithm, simulation operation circuit.Keywords：structure ，working principle，The basic principle of the circuit ，The practical application绪论：模拟运算放大器从诞生至今，已有40多年的历史了。

运算放大器最早被设计出来的目的是用来进行加、减、微分、积分的模擬数学运算，因此被称为“运算放大器。

直流放大电路在工业技术领域中，特别是在一些测量仪器和自动化控制系统中应用非常广泛。

如在一些自动控制系统中，首先要把被控制的非电量（如温度、转速、压力、流量、照度等）用传感器转换为电信号，再与给定量比较，得到一个微弱的偏差信号。

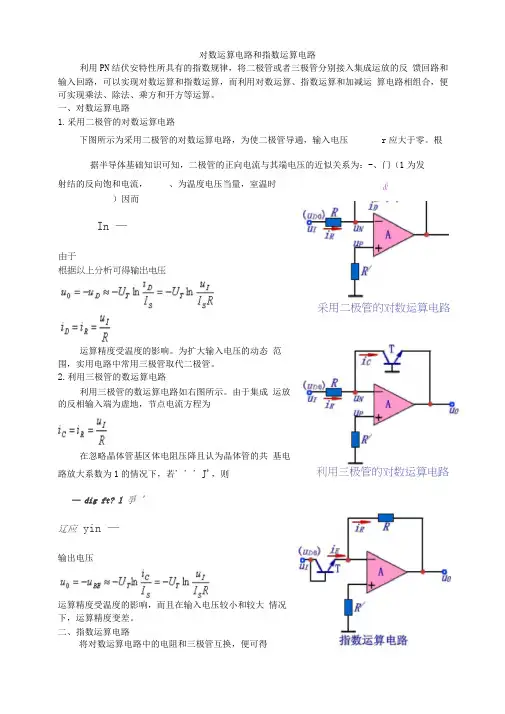
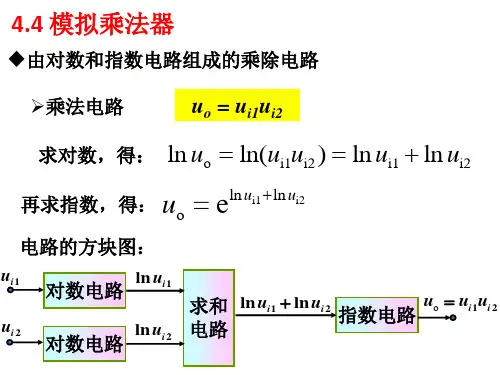
对数运算电路和指数运算电路利用PN结伏安特性所具有的指数规律，将二极管或者三极管分别接入集成运放的反馈回路和输入回路，可以实现对数运算和指数运算，而利用对数运算、指数运算和加减运算电路相组合，便可实现乘法、除法、乘方和开方等运算。

一、对数运算电路1.采用二极管的对数运算电路下图所示为采用二极管的对数运算电路，为使二极管导通，输入电压r应大于零。

根据半导体基础知识可知，二极管的正向电流与其端电压的近似关系为：-、门（1为发射结的反向饱和电流，、为温度电压当量，室温时）因而In —运算精度受温度的影响。

为扩大输入电压的动态范围，实用电路中常用三极管取代二极管。

2.利用三极管的数运算电路利用三极管的数运算电路如右图所示。

由于集成运放的反相输入端为虚地，节点电流方程为在忽略晶体管基区体电阻压降且认为晶体管的共基电路放大系数为1的情况下，若' ' ' J'，则— dig ft? l 爭 '辽应 yin —输出电压运算精度受温度的影响，而且在输入电压较小和较大情况下，运算精度变差。

二、指数运算电路将对数运算电路中的电阻和三极管互换，便可得采用二极管的对数运算电路由于根据以上分析可得输出电压利用三极管的对数运算电路&到指数运算电路，如右图所示。

因为集成运放反相输入端为虚地，所以応協=囂』S 二❻咼z*叶输出电压为使晶体管导通，=应大于零，且只能在发射结导通电压范围内， 故其变化范围很小。

由 于运算结果与受温度影响较大的 •有关，因而指数运算的精度也与温度有关改进电路1:用三极管代替二极管lc一 VliE = Vo = -V T 111 — = -V T 111电路在理想情况下可完全消除温度的影响改进电路3:实用对数电路如果忽略T 2基极电流， 则M 点电位：-1)V/iE = L(e liVBE=Le °(皿 » % Vi2/¥的iVol a= —P/lll RLLR 1IR 1RLRf R f v nR”如果取Rf 并令1(1 +罟)!亍刼df\4则 = -ATlgj^8.4.2指数电路1.基本指数电路2ZVo = —RI S €]V/ » V T时21in 乞 Le 1J= /R =—所以P5n-r ；lllV B =IR I L14 = KlnR 山Vo =R. TJ-(1 + —"iH 「M )R A= - ------------- Vo — V BEI — V 阳川+ /6由 丁- ici = I n lei = I RVoR^Rz«. + «： V RR\ l r f也=（1+—炸1（）八Ri=K E2.反函数型指数电路电路必须是负反馈才能正常工作，所以:-昨。

模拟运算电路一、实验目的1、研究由集成运算放大器组成的比例、加法、减法和积分等基本运算电路的功能。

2、了解运算放大器在实际应用时应考虑的一些问题。

二、实验原理集成运算放大器是一种具有高电压放大倍数的直接耦合多级放大电路。

当外部接入不同的线性或非线性元器件组成输入和负反馈电路时，可以灵活地实现各种特定的函数关系。

在线性应用方面，可组成比例、加法、减法、积分、微分、对数等模拟运算电路。

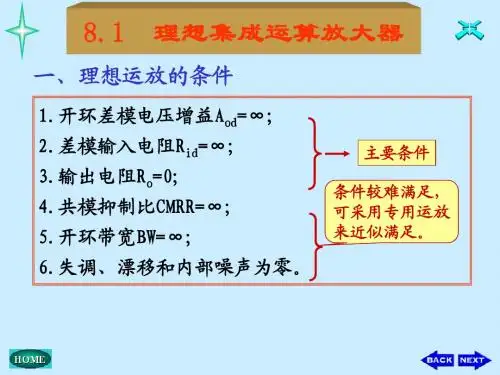
1、理想运算放大器特性在大多数情况下，将运放视为理想运放，就是将运放的各项技术指标理想化，满足下列条件的运算放大器称为理想运放。

开环电压增益 A ud =∞ 输入阻抗 r i =∞ 输出阻抗 r o =0 带宽 f BW =∞ 2、失调与漂移均为零等。

理想运放在线性应用时的两个重要特性：（1）输出电压U O 与输入电压之间满足关系式U O ＝A ud （U +－U －）由于A ud =∞，而U O 为有限值，因此，U +－U －≈0。

即U +≈U －，称为“虚短”。

（2）由于r i =∞，故流进运放两个输入端的电流可视为零，即I IB ＝0，称为“虚断”。

这说明运放对其前级吸取电流极小。

上述两个特性是分析理想运放应用电路的基本原则，可简化运放电路的计算。

3、基本运算电路 1) 反相比例运算电路电路如图7－1所示。

对于理想运放， 该电路的输出电压与输入电压之间的关系为（2-1） 为了减小输入级偏置电流引起的运算误差，在同相输入端应接入平衡电阻R 2＝R 1 / R F 。

图2－1 反相比例运算电路 图2－2 反相加法运算电路2) 反相加法电路i 1FO U R R U -=电路如图2－2所示，输出电压与输入电压之间的关系为)U R RU R R (U i22F i11F O +-= R 3＝R 1 // R 2 // R F （2-2） 3) 同相比例运算电路图2－3(a)是同相比例运算电路，它的输出电压与输入电压之间的关系为i 1FO )U R R (1U += R 2＝R 1 / R F （2-3）(a) 同相比例运算电路 (b) 电压跟随器图2-3 同相比例运算电路当R 1→∞时，U O ＝U i ，即得到如图2－3(b)所示的电压跟随器。

运算放大器应用电路的设计与制作(一） 运算放大器 1.原理运算放大器是目前应用最广泛的一种器件,当外部接入不同的线性或非线性元器件组成输入和负反响电路时，可以灵敏地实现各种特定的函数关系。

在线性应用方面，可组成比例、加法、减法、积分、微分、对数等模拟运算电路。

运算放大器一般由4个局部组成，偏置电路，输入级，中间级，输出级。

图1运算放大器的特性曲线 图2运算放大器输入输出端图示图1是运算放大器的特性曲线，一般用到的只是曲线中的线性局部。

如图2所示。

U -对应的端子为“-〞，当输入U -单独加于该端子时，输出电压与输入电压U -反相，故称它为反相输入端。

U +对应的端子为“＋〞，当输入U +单独由该端参加时，输出电压与U +同相，故称它为同相输入端。

输出：U 0= A(U +-U -) ； A 称为运算放大器的开环增益〔开环电压放大倍数〕。

在实际运用经常将运放理想化，这是由于一般说来，运放的输入电阻很大，开环增益也很大，输出电阻很小，可以将之视为理想化的，这样就能得到:开环电压增益A ud =∞；输入阻抗r i =∞；输出阻抗r o =0；带宽f BW =∞；失调与漂移均为零等理想化参数。

2.理想运放在线性应用时的两个重要特性输出电压U O 与输入电压之间满足关系式：U O ＝A ud 〔U +－U －〕,由于A ud =∞，而U O 为有限值，因此，U +－U －≈0。

即U +≈U －，称为“虚短〞。

由于r i =∞，故流进运放两个输入端的电流可视为零，即I IB ＝0，称为“虚断〞,这说明运放对其前级汲取电流极小。

上述两个特性是分析理想运放应用电路的根本原那么，可简化运放电路的计算。

3. 运算放大器的应用 (1)比例电路所谓的比例电路就是将输入信号按比例放大的电路，比例电路又分为反向比例电路、同相比例电路、差动比例电路。

(a) 反向比例电路反向比例电路如图3所示，输入信号参加反相输入端:图3反向比例电路电路图对于理想运放，该电路的输出电压与输入电压之间的关系为：为了减小输入级偏置电流引起的运算误差，在同相输入端应接入平衡电阻R ’＝R 1 // R F 。

第7章集成运放组成的运算电路本章教学基本要求本章介绍了集成运放的比例、加减、积分、微分、对数、指数和乘法等模拟运算电路及其应用电路以及集成运放在实际应用中的几个问题。

表为本章的教学基本要求。

学完本章后应能运用虚短和虚断概念分析各种运算电路，掌握比例、求和、积分电路的工作原理和输岀与输入的函数关系，理解微分电路、对数运算电路、模拟乘法器的工作原理和输出与输入的函数关系，并能根据需要合理选择上述有关电路。

本章主要知识点1.集成运放线性应用和非线性应用的特点由于实际集成运放与理想集成运放比较接近，因此在分析、计算应用电路时，用理想集成运放代替实际集成运放所带来的误差并不严重，在一般工程计算中是允许的。

本章中凡未特别说明，均将集成运放视为理想集成运放。

集成运放的应用划分为两大类：线性应用和非线性应用。

（1）线性应用及其特点集成运放工作在线性区必须引入深度负反馈或是兼有正反馈而以负反馈为主，此时苴输出量与净输入量成线性关系，但是整个应用电路的输出和输入也可能是非线性关系。

集成运放工作在线性区时，它的输出信号/和输入信号（同相输入端"+和反相输入端〃一之差）满足式（7-1）〃。

=尙0+-工）（7-1）在理想情况下，集成运放工作于线性区满足虚短和虚断。

虚短：是指运放两个输入端之间的电压几乎等于零：虚断：是指运放两个输入端的电流几乎等于零。

即虚短：LL-U+"或虚断：/_ = /+能0(2)非线性应用及其特点非线性应用中集成运放工作在非线性区，电路为开坏或正反馈状态，集成运放的输出量与净输入量成非线性关系人工A°dQ_-6/+)。

输入端有很微小的变化量时，输出电压为正饱和电压或负饱和电压值(饱和电压接近正、负电源电压)，u_=u+为两种状态的转折点。

即当u_>u+时，u o = u OL当时，U°=U OH非线性应用中，集成运放在理想情况下，满足虚断，即/_=/+«0o2.运算电路及其分析方法基本运算电路的共同特点是集成运放接成负反馈形式，工作在线性放大状态，集成运放满足虚短和虚断。

对数计算方法及对数计算电路对数计算在近代科学发展过程中占有重要地位，它是用于求解复杂计算问题的方法之一，包括科学计算、工程优化、信号处理等等。

根据需要，近年来出现了不同类型的对数计算电路，它们不仅提高了计算效率，而且易于节省能源、实现大规模集成。

本文将介绍对数计算方法和对应电路，并分析其特点。

一、对数计算方法1.什么是对数计算对数计算是指利用对数的性质，将复杂的运算问题转化为求解对数的形式来解决。

它是用于求解复杂计算问题的一种方法，主要应用于多项式求根、多项式计算以及科学计算、工程优化、信号处理等等。

例如，在科学计算中，求解积分、求解微积分等问题都可以使用对数计算来解决；而在工程优化中，求解非线性规划、优化规划等问题也可以应用对数计算。

几乎在所有的高级数据处理系统中，都会使用对数计算的方法。

2.基本原理对数的性质是，当一个数的对数值变化时，其值会受到影响。

如果能将复杂的运算问题转换成求解多个对数值的形式，再根据得到的多个对数值求解原始问题，这便是对数计算的基本原理。

对数计算电路1.什么是对数计算电路对数计算电路是根据对数计算方法设计的电路，用于实现快速、高效的复杂数学计算，是用于解决复杂计算问题的电子设备。

它们通常由一系列的数字电路和时栅电路组成，可以实现连续的对数计算。

2.特点（1）高效率：对数计算电路具有极高的运算效率，能够大大提高计算效率，并减少运算时间。

（2）简单性：对数计算电路结构简单，容易实现，不需要过多的组件。

（3）节能：对数计算电路处理运算任务时，耗电能量较小，节能效果明显。

（4）易于集成：对数计算电路组件简单，易于大规模集成，可以满足不同需求，提高环节中处理能力。

综上所述，对数计算方法在科学计算、工程优化、信号处理等方面都能发挥重要作用，而对数计算电路则可以使得这种计算更加的高效、节能、简单，所以对数计算方法及电路对现代科学技术的发展至关重要。

对数运算电路
1．对数运算电路
图 1
利用半导体PN结的指数型伏安特性，可以实现对数运算。

实用时常将BJT的集电极与基极短路。

接成二极管形式，则在一个相当宽广的范围内（如IC从10–9~10–3A），集电极电流IC与发射极电压VBE 之间具有较为精确的对数关系。

BJT的iC~vBE的关系为
这是因为一般有vBE>>VT（在室温300K时，VT?26mV）。

由此可得
对数运算电路如图XX_01所示，由，，可得
可见，输出电压和输入电压成对数关系。

输出电压的幅度不能超过0.7V，且要求vs>0，以保证晶体管处于导通状态。

2．具有温度补偿电路
图 2
由于VT和IES对温度敏感，输出电压温漂较严重，为此，实际的对数电路都采用温度补偿电路。

图2所示电路可以实现温度补偿。

图中T1、T2两管发射结电压分别为
由于T1、T2为对管，IES1= IES2，可求得
忽略T2的基极电流，，则
式中VT与温度有关，若电阻Rt具有正温度系数，在一定温度范围内可补偿VT的温度影响。

另外，调节R3的值可扩大输出电压，使之超过0.7V。