假设检验及单样本检验

SPSS假设检验1. 简介SPSS（Statistical Package for the Social Sciences）是一种非常常用的统计软件，被广泛应用于社会科学研究中。

其中，假设检验是SPSS中常用的统计方法之一，用于验证研究者对总体或样本的某种假设。

2. 假设检验的概念假设检验是统计学中的一种重要方法，用于判断一个统计推断是否与样本数据一致。

在假设检验中，通常会提出一个原假设（H0）和一个备择假设（H1），然后根据样本数据对两个假设进行检验，以确定是否拒绝原假设，从而对总体进行推断。

3. SPSS中的假设检验SPSS中提供了丰富的假设检验方法，涵盖了多种统计推断的情况。

下面将介绍几种常见的假设检验方法。

3.1 单样本 t 检验单样本 t 检验用于判断一个样本的均值是否与一个已知的常数有显著性差异。

在SPSS中，进行单样本 t 检验的步骤如下：1.导入数据：在SPSS中打开或导入数据文件。

2.选择变量：选择要进行 t 检验的变量。

3.进行检验：选择菜单栏上的“分析”-“比较均值”-“单样本 t 检验”。

4.设置参数：选择相关的变量和检验参数，点击“确定”进行分析。

5.查看结果：SPSS将显示 t 检验的结果，包括均值、标准差、t 值、自由度和显著性等。

3.2 独立样本 t 检验独立样本 t 检验用于判断两个独立样本的均值是否存在显著性差异。

在SPSS中，进行独立样本 t 检验的步骤如下：1.导入数据：在SPSS中打开或导入数据文件。

2.选择变量：选择需要进行对比的两个变量。

3.进行检验：选择菜单栏上的“分析”-“比较均值”-“独立样本 t 检验”。

4.设置参数：选择相关的变量和检验参数，点击“确定”进行分析。

5.查看结果：SPSS将显示独立样本 t 检验的结果，包括均值、标准差、t 值、自由度和显著性等。

3.3 配对样本 t 检验配对样本 t 检验用于判断同一组个体在两个不同时间点或条件下的均值是否存在显著性差异。

单样本和双样本假设检验1. 引言在统计学中，假设检验是一种常用的统计推断方法，用于检验关于总体参数的假设是否成立。

假设检验可以根据样本数据对总体参数进行推断，并通过计算得出统计量的概率（P值），从而判断原假设是否应被拒绝。

在假设检验中，常用的方法包括单样本和双样本假设检验。

2. 单样本假设检验单样本假设检验主要用于检验一个样本是否来自某一特定总体。

其步骤如下：2.1 建立假设首先需要建立研究假设，包括原假设（H0）和备择假设（H1）。

原假设通常表示无效、无差异或无影响的假设，备择假设则表示相反的情况。

2.2 选择统计量根据研究问题和数据类型选择适当的统计量。

常见的统计量包括均值、比例、方差等。

2.3 计算统计量的值使用样本数据计算统计量的值。

例如，对于均值，可以使用样本均值来估计总体均值。

2.4 确定显著水平显著水平（α）表示拒绝原假设的程度，通常取0.05或0.01。

根据显著水平确定拒绝域。

2.5 计算P值根据原假设、样本数据和选择的统计量计算P值。

P值是在原假设成立的情况下，观察到统计量或更极端情况发生的概率。

较小的P值表示较强的证据反对原假设。

2.6 做出统计决策根据P值和显著水平，做出统计决策。

通常，如果P值小于显著水平，则拒绝原假设；反之，则接受原假设。

3. 双样本假设检验双样本假设检验适用于比较两个独立样本之间的差异。

其步骤如下：3.1 建立假设同样需要建立原假设和备择假设，区别在于原假设研究的是两个样本的差异是否为零。

3.2 选择统计量通常选择两个样本的差异（如均值差）作为统计量。

3.3 计算统计量的值使用样本数据计算统计量的值。

例如，计算两个样本的均值差。

3.4 确定显著水平与单样本假设检验相同，确定显著水平。

3.5 计算P值根据原假设、样本数据和选择的统计量计算P值。

3.6 做出统计决策根据P值和显著水平，做出统计决策。

4. 总结单样本和双样本假设检验是统计学中常用的推断方法，用于检验关于总体参数的假设是否成立。

常见假设检验公式概览假设检验是统计学中一种重要的推断方法，用于判断总体参数的真实情况。

在假设检验中，我们通常会提出一个原假设和一个备择假设，并通过采样数据来判断是否拒绝原假设。

在实际应用中，常见的假设检验方法有如下几种。

1. 单样本均值检验单样本均值检验用于判断一个样本的平均值是否等于一个已知的常数。

其中，我们常用的假设检验公式为：t = (x - μ) / (s / √n)其中，t表示t值，x为样本均值，μ为总体均值，s为样本标准差，n为样本容量。

通过比较t值与临界值，我们可以判断是否拒绝原假设。

2. 双独立样本均值检验双独立样本均值检验用于比较两个独立样本的平均值是否相等。

常用的假设检验公式如下：t = (x1 - x2) / √(s1²/n1 + s2²/n2)其中，t表示t值，x1和x2分别为两个样本的均值，s1和s2为两个样本的标准差，n1和n2为两个样本的容量。

通过比较t值和临界值，可以判断是否拒绝原假设。

3. 配对样本均值检验配对样本均值检验用于比较同一组样本的两个相关变量的平均值是否相等。

常用的假设检验公式如下：t = (x d - μd) / (sd / √n)其中，t表示t值，x d为配对差值的均值，μd为总体差值的均值，sd为配对差值的标准差，n为配对样本容量。

通过比较t值和临界值，可以得出是否拒绝原假设。

4. 单样本比例检验单样本比例检验用于判断一个样本比例是否等于一个已知的比例。

常用的假设检验公式如下：z = (p - π) / √(π(1-π)/n)其中，z表示z值，p为样本比例，π为总体比例，n为样本容量。

通过比较z值和临界值，可以判断是否拒绝原假设。

5. 独立样本比例检验独立样本比例检验用于比较两个独立样本的比例是否相等。

常用的假设检验公式如下：z = (p1 - p2) / √(p(1-p)(1/n1 + 1/n2))其中，z表示z值，p1和p2分别为两个样本的比例，n1和n2分别为两个样本的容量。

单样本比例假设检验在统计学中，假设检验是一种用来判断一个假设是否成立的方法。

单样本比例假设检验是一种用于检验一个总体比例是否等于某个特定值的统计方法。

本文将介绍单样本比例假设检验的原理、步骤以及如何进行。

一、原理单样本比例假设检验的原理是基于二项分布的概率。

在假设检验中，我们假设一个总体的比例为p，然后通过对观察到的样本数据进行统计推断，判断p是否等于某个特定值。

假设检验的目的是帮助我们做出关于总体的推断，从而对现象进行解释和预测。

二、步骤进行单样本比例假设检验需要以下步骤：1. 提出假设：首先，我们需要提出原假设（H0）和备择假设（Ha）。

原假设通常是我们想要证明的假设，备择假设则是对原假设的互补或者相反的假设。

2. 设置显著性水平：显著性水平（α）是我们在假设检验中设置的一个阈值，用来判断是否拒绝原假设。

通常情况下，显著性水平取0.05或0.01。

3. 计算检验统计量：接下来，我们需要计算检验统计量。

对于单样本比例假设检验，常用的检验统计量是Z值，计算公式为：Z = (p - p0) / sqrt((p0 * (1 - p0)) / n)其中，p是样本比例，p0是假设的比例值，n是样本容量。

4. 确定拒绝域：拒绝域是根据显著性水平和检验统计量的分布来确定的。

如果检验统计量落在拒绝域内，就可以拒绝原假设。

5. 判断结果：根据拒绝域的判断，我们可以得出对原假设的结论。

如果检验统计量落在拒绝域内，我们可以拒绝原假设，认为样本提供了足够的证据来支持备择假设。

如果检验统计量没有落在拒绝域，我们无法拒绝原假设，即无法得出统计上的显著结果。

三、实例为了更好地理解单样本比例假设检验的应用，我们来举一个实例。

假设某个公司宣称其产品的合格率达到了75%。

为了验证这个宣称是否可信，我们从该公司生产的产品中随机抽取了100个样本，并统计发现其中有65个样本合格。

现在我们需要进行单样本比例假设检验。

1. 提出假设：原假设H0：产品的合格率为75%；备择假设Ha：产品的合格率不等于75%。

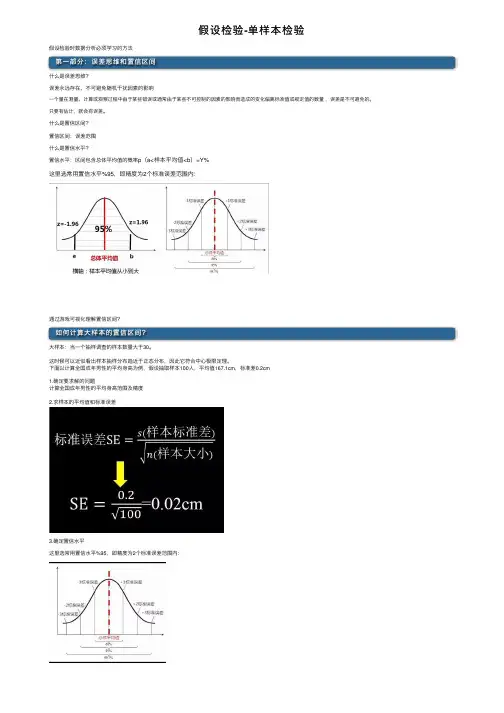
假设检验-单样本检验假设检验时数据分析必须学习的⽅法第⼀部分：误差思维和置信区间什么是误差思维？误差永远存在、不可避免随机⼲扰因素的影响⼀个量在测量、计算或观察过程中由于某些错误或通常由于某些不可控制的因素的影响⽽造成的变化偏离标准值或规定值的数量，误差是不可避免的。

只要有估计，就会有误差。

什么是置信区间？置信区间：误差范围什么是置信⽔平？置信⽔平：区间包含总体平均值的概率p（a<样本平均值<b）=Y%这⾥选常⽤置信⽔平%95，即精度为2个标准误差范围内：通过游戏可视化理解置信区间？如何计算⼤样本的置信区间？⼤样本：当⼀个抽样调查的样本数量⼤于30。

这时候可以近似看出样本抽样分布趋近于正态分布，因此它符合中⼼极限定理。

下⾯以计算全国成年男性的平均⾝⾼为例，假设抽取样本100⼈，平均值167.1cm，标准差0.2cm 1.确定要求解的问题计算全国成年男性的平均⾝⾼范围及精度2.求样本的平均值和标准误差3.确定置信⽔平这⾥选常⽤置信⽔平%95，即精度为2个标准误差范围内：4.求出置信区间上下限的值（1）由于选⽤的样本⼤⼩为100⼤于30符合正态分布，先求出如下图中两块红⾊区域⾯积（概率）：（2）通过查z表格查出标准分Z=-1.96（3）求出a和b的值的⽅法：（4）根据中⼼极限定理，样本平均值约等于总体平均值，最终求出a和b的值：结论：当我们选⽤置信⽔平为%95时，求得置信区间为[167.0608,167.1392]，即在两个标准误差范围内，全国成年男性的平均⾝⾼为167.0608cm到167.1392cm之间。

5.常⽤置信⽔平及其对应Z值（标准分）如何计算⼩样本的置信区间？⼩样本：当⼀个抽样调查的样本数量⼩于30。

这时候抽样分布符合t分布：在概率论和统计学中，t-分布（t-distribution）⽤于根据⼩样本来估计呈正态分布且⽅差未知的总体的均值。

如果总体⽅差已知（例如在样本数量⾜够多时），则应该⽤正态分布来估计总体均值。

假设检验的八种情况的公式假设检验是统计学中常用的一种方法，用于判断样本数据与总体参数的关系是否具有显著性差异。

在进行假设检验时，我们需要根据实际问题和已知条件确定相应的假设检验公式。

以下是八种常见的假设检验情况及相应的公式。

1.单样本均值检验：在这种情况下，研究者想要判断一个样本的均值是否与一个已知的总体均值有显著性差异。

假设检验的公式为：其中，x̄为样本均值，μ为总体均值，s为样本标准差，n为样本容量，t为t分布的临界值。

2.双样本均值检验（方差已知）：在这种情况下，研究者想要判断两个样本的均值是否有显著性差异，且已知两个样本的方差相等。

假设检验的公式为：其中，x̄1和x̄2分别为样本1和样本2的均值，μ1和μ2分别为总体1和总体2的均值，s为样本标准差，n1和n2分别为样本1和样本2的容量，z为标准正态分布的临界值。

3.双样本均值检验（方差未知）：在这种情况下，研究者想要判断两个样本的均值是否有显著性差异，且两个样本的方差未知且不相等。

假设检验的公式为：其中，x̄1和x̄2分别为样本1和样本2的均值，μ1和μ2分别为总体1和总体2的均值，s1和s2分别为样本1和样本2的标准差，n1和n2分别为样本1和样本2的容量，t为t分布的临界值。

4.单样本比例检验：在这种情况下，研究者想要判断一个样本的比例是否与一个已知的总体比例有显著性差异。

假设检验的公式为：其中，p̄为样本比例，p为总体比例，n为样本容量，z为标准正态分布的临界值。

5.双样本比例检验：在这种情况下，研究者想要判断两个样本的比例是否有显著性差异。

假设检验的公式为：其中，p̄1和p̄2分别为样本1和样本2的比例，p1和p2分别为总体1和总体2的比例，n1和n2分别为样本1和样本2的容量，z为标准正态分布的临界值。

6.简单线性回归检验：在这种情况下，研究者想要判断自变量与因变量之间的线性关系是否显著。

假设检验的公式为：其中，β1为回归系数，se(β1)为标准误差，t为t分布的临界值。

常见假设检验公式的详细解析假设检验是统计学中常用的一种推断方法，用于判断一个假设是否成立。

常见的假设检验公式有很多种，下面将对其中几种进行详细解析。

1. 单样本均值检验公式假设我们有一组观测值X₁，X₂，...，Xₙ，要检验这些观测值的总体均值是否等于某个值μ₀。

假设检验的原假设（H₀）是：总体均值等于μ₀，备择假设（H₁）是：总体均值不等于μ₀。

使用t检验进行检验时，计算统计量的公式如下：t = (x - μ₀) / (s/√n)其中，x是样本均值，s 是样本标准差，n 是样本容量。

根据t值和自由度的对应表，可以得到该t值的显著性水平和p值。

2. 双样本均值检验公式双样本均值检验用于比较两组样本的均值是否有显著差异。

假设我们有两组样本X₁，X₂，...，Xₙ和Y₁，Y₂，...，Yₙ，要检验它们的总体均值是否相等。

使用独立样本t检验进行检验时，计算统计量的公式如下：t = (x₁ - x₂) / √((s₁²/n₁) + (s₂²/n₂))其中，x₁和x₂分别是两组样本的均值，s₁和 s₂分别是两组样本的标准差，n₁和 n₂分别是两组样本的容量。

根据t值和自由度的对应表，可以得到该t值的显著性水平和p值。

3. 单样本比例检验公式单样本比例检验用于检验样本的比例是否等于某个给定的比例。

假设我们有一组观测值，成功的事件发生的次数为x，总事件发生的次数为n，要检验成功的概率是否等于某个给定的比例p₀。

使用正态分布的近似方法进行检验时，计算统计量的公式如下：z = (p - p₀) / √(p₀(1-p₀)/n)其中，p是样本成功的比例，p₀是给定的比例，n 是样本容量。

根据z值和显著性水平的对应关系，可以得到该z值的p值。

总结：上述所介绍的是常见假设检验公式中的几种，每种假设检验有其适用的前提条件和计算公式。

在进行假设检验时，需要注意选择适当的公式和假设检验方法，以及正确计算统计量并进行显著性检验。

假设检验与样本数量分析③——单方差检验双方差检验假设检验和样本数量分析是统计学中常用的分析方法之一，用于确定统计推断的有效性和结果的可靠性。

在假设检验中，我们通常会涉及到单方差检验和双方差检验，用于比较两个或多个总体的方差是否相等。

下面将详细介绍这两个检验方法，并介绍样本数量分析的重要性。

单方差检验用于比较两个总体的方差是否相等。

该检验的原假设（H0）为两个总体的方差相等，备择假设（H1）为两个总体的方差不相等。

我们使用F检验进行单方差检验，计算检验统计量F值，并将其与临界值进行比较。

如果F值显著大于临界值，则拒绝原假设，说明两个总体的方差不相等。

双方差检验也用于比较两个总体的方差是否相等，但与单方差检验不同的是，双方差检验是在两个样本的情况下进行的。

该检验的原假设（H0）为两个总体的方差相等，备择假设（H1）为两个总体的方差不相等。

我们使用Bartlett检验进行双方差检验，计算检验统计量B值，并将其与临界值进行比较。

如果B值显著大于临界值，则拒绝原假设，说明两个总体的方差不相等。

在进行单方差检验和双方差检验之前，我们需要进行样本数量分析，以确定合适的样本数量。

样本数量的选择将直接影响统计推断的有效性和结果的可靠性。

样本数量分析的目标是使得检验具有统计功效（即检验能够准确地拒绝错误的原假设）。

进行样本数量分析需要考虑以下因素：显著性水平、类型I错误的控制、效应大小和统计功效。

显著性水平是我们设定的接受或拒绝原假设的标准，通常为0.05、类型I错误是拒绝了正确的原假设，通常被设定为显著性水平的大小。

效应大小是总体之间存在差异的程度，可以用标准差或差异值来衡量。

统计功效是检验能够正确拒绝错误原假设的概率。

根据样本数量的选择准则，我们可以选择合适的样本数量以确保统计推断的有效性和结果的可靠性。

通常，样本数量应该足够大以使得统计功效达到要求并控制类型I错误的发生概率。

样本数量的规定一般是根据预先设定的最小效应大小、显著性水平、统计功效和样本分析方法来确定。

假设检验公式单样本与双样本假设检验方差分析的计算方法假设检验公式：单样本与双样本假设检验方差分析的计算方法假设检验是统计学中非常重要的一种方法，用于判断一个样本或两个样本之间的差异是否显著。

而在进行假设检验时，我们通常需要计算一些统计量来评估样本数据的差异性。

本文将介绍单样本与双样本假设检验方差分析的计算方法。

一、单样本假设检验方差分析的计算方法在进行单样本假设检验时，我们关注的是一个样本的均值与总体均值之间是否存在显著差异。

常用的单样本假设检验方法有t检验和z检验，其中z检验用于大样本情况下，而t检验适用于小样本情况。

计算方法如下：1. 计算样本均值（x_bar）和样本标准差（s）。

2. 计算标准误差（SE），公式为：SE = s / √n其中，n为样本数量。

3. 设定显著性水平（α），一般为0.05或0.01。

4. 根据显著性水平和自由度（df）查找相应的t或z分布表，得到相应的临界值（t_critical或z_critical）。

t = (x_bar - μ) / SE或z = (x_bar - μ) / SE其中，μ为总体均值。

6. 比较计算得到的t或z值与临界值，判断是否拒绝原假设。

如果计算得到的t或z值大于或小于临界值，拒绝原假设，说明样本均值与总体均值存在显著差异；反之，接受原假设，说明差异不显著。

二、双样本假设检验方差分析的计算方法双样本假设检验用于比较两个样本之间的差异是否显著。

在进行双样本假设检验时，我们可以使用t检验或z检验来进行推断。

1. 计算两个样本的均值（x1_bar和x2_bar）、标准差（s1和s2）和样本数量（n1和n2）。

2. 计算两个样本的标准误差（SE1和SE2），公式为：SE1 = s1 / √n1SE2 = s2 / √n23. 设定显著性水平（α）和自由度（df）。

4. 查找相应的t或z分布表，得到临界值（t_critical或z_critical）。

统计学假设检验公式整理统计学假设检验是统计学中常用的一种方法。

通过使用统计学的方法，我们可以根据样本数据对总体的某种假设进行检验，以确定该假设是否得到支持。

在进行假设检验时，我们需要使用一些公式来计算统计量，从而得到检验结果。

本文将对常见的统计学假设检验公式进行整理和介绍。

一、单样本均值假设检验公式单样本均值假设检验用于确定总体均值是否与给定值相等。

常见的统计学公式包括：1. Z检验公式Z检验适用于大样本（样本容量大于30）的情况，公式如下：$$Z = \frac{\overline{x} - \mu}{\frac{\sigma}{\sqrt{n}}}$$其中，$\overline{x}$ 表示样本均值，$\mu$ 表示总体均值，$\sigma$ 表示总体标准差，$n$ 表示样本容量。

2. t检验公式t检验适用于样本容量较小（30以下）或总体标准差未知的情况，公式如下：$$t = \frac{\overline{x} - \mu}{\frac{s}{\sqrt{n}}}$$其中，$\overline{x}$ 表示样本均值，$\mu$ 表示总体均值，$s$ 表示样本标准差，$n$ 表示样本容量。

双样本均值假设检验常用于比较两个样本之间的均值是否有显著差异。

常见的统计学公式包括：1. 独立双样本t检验公式独立双样本t检验适用于两个样本是相互独立的情况，公式如下：$$t = \frac{(\overline{x}_1 - \overline{x}_2) - (\mu_1 -\mu_2)}{\sqrt{\frac{{s_1}^2}{n_1} + \frac{{s_2}^2}{n_2}}}$$其中，$\overline{x}_1$ 和 $\overline{x}_2$ 分别表示第一个样本和第二个样本的均值，$\mu_1$ 和 $\mu_2$ 分别表示第一个总体和第二个总体的均值，$s_1$ 和 $s_2$ 分别表示第一个样本和第二个样本的标准差，$n_1$ 和 $n_2$ 分别表示第一个样本和第二个样本的容量。