单样本KS检验

ks检验结果解读-回复如何解读KS检验结果及其意义1. 什么是KS检验KS检验（Kolmogorov-Smirnov test）是一种常用的非参数假设检验方法，用于判断两个样本是否来自同一个总体分布。

它通过比较两个样本的经验分布函数（ECDF）的差异，判断它们是否有显著性差异。

2. KS检验的原理KS检验的原理是比较两个样本的经验分布函数（ECDF）与其理论累积分布函数（CDF）之间的差异。

在同一总体假设下，两个样本的ECDF与CDF 应该非常接近，差异较小。

若差异大到一定程度，就可以拒绝两个样本来自同一总体分布的假设。

3. KS检验的假设在对KS检验结果进行解读前，需要明确KS检验的两个假设：- 零假设（H0）：两个样本来自同一总体分布。

- 备择假设（H1）：两个样本不来自同一总体分布。

4. KS检验结果的解读KS检验的结果通常包括两个统计量：D值和p值。

(1) D值D值是KS检验的统计量，表示两个样本ECDF与CDF的最大差异。

D值的计算公式为：D = max F1(x) - F2(x) ，其中F1(x)和F2(x)分别是两个样本的ECDF。

D值的具体含义是：两个样本的最大差异程度。

如果D值较小，则说明两个样本的分布较为相似；如果D值较大，则说明两个样本的分布有较大差异。

(2) p值p值是KS检验的显著性水平，表示在零假设成立的条件下，获得观察到的差异或更极端结果的概率。

对于KS检验而言，p值的含义是：在两个样本来自同一总体分布的假设下，观察到的差异或更极端结果的概率。

如果p值较小（通常小于0.05），则拒绝零假设，认为两个样本不来自同一总体分布；如果p值较大（通常大于0.05），则无法拒绝零假设，即不能得出两个样本有显著性差异的结论。

5. KS检验结果的意义KS检验作为一种非参数假设检验方法，具有以下几个特点和适用场景：(1) 无需假设总体分布的形式：KS检验无需知道总体分布的具体形式，只需比较两个样本的分布差异即可。

非参数卡方检验1.理论非参数检验是在总体分布未知或知道甚少的情况下，不依赖于总体布形态，在总体分布情况不明时，用来检验不同样本是否来自同一总体的统计方法进。

由于非参数检验方法在推断过程中不涉及有关总体分布的参数，因而得名为“非参数”检验。

非参数检验优势：检验条件宽松，适应性强。

针对，非正态、方差不等的已及分布形态未知的数据均适用。

检验方法灵活，用途广泛。

运用符号检验、符号秩检验解决不能直接进行四则运算的定类和定序数据。

非参数检验的计算相对简单，易于理解。

但非参数检验方法对总体分布假定不多，缺乏针对性，且使用的是等级或符号秩，而不是实际数值，容易失去较多信息。

非参数卡方检验：用于检验样本数据的分布是否与某种特定分布情况相同。

非参数卡方检验通过三步检验：1.卡方统计量：X2=B 其中K 是样本分类的个数，0表示实际观测的频数，B 表示理论分布下的频数。

2.拟合优度检验：A.对总体分布建立假设。

B.抽样并编制频率分布表。

C.以原假设为真，导出期望频率。

D.计算统计量。

E.确定自由度，并查x2表，得到临界值。

F.比较x2值与临界值，做出判断。

3.独立性检验A.对总体分布建立假设。

B.抽样并编制r*c 列联表。

C.计算理论频数。

D.计算检验统计量。

E.确定自由度，并查x2表，得到临界值。

F.比较x2值与临界值，做出判断。

2.非参数卡方检验操作步骤第一步：将需检验的数据导入spss中并进行赋值后，点击分析非参数检验、旧对话框、卡方。

图2操作步骤第一步第二步：进入图中对话框后点击，首先将需检验的数据放入检验变量列表中，后在期望值选项中所以类别相等或者值（值：需要手动输入具体的分布情况）。

如果特殊情况需要调整检验置信区间，点击精确，进入图中下方对话框后点击蒙特卡洛法框里收到填入。

点击继续、确定。

图3操作步骤第二步第三步：如果需要看描述统计结果和四分位数值可以点击选项、勾选描述、四分位数。

点击继续、确实。

图4操作步骤第二步3.非参数卡方检验结果然后非参数卡方检验的描述统计、卡方检验频率表、检验统计结果就出来了。

ks检验结果解读-回复KS检验结果解读及其应用：一步一步回答引言：在统计学中，KS检验（Kolmogorov-Smirnov test）是一种非参数检验方法，用于比较两个样本的分布是否相同。

KS检验可以帮助我们判断两个样本是否来自同一总体分布，或者在统计分析中找出两个样本之间的差异性。

本文将介绍KS检验的原理、应用，以及如何解读其结果。

第一步：KS检验的原理解释KS检验是通过比较两个累积分布函数（CDF）之间的最大差异来判断两个样本的分布是否相同。

假设我们有两个样本：样本1和样本2。

1. 零假设（H0）：样本1和样本2来自同一总体分布。

2. 备择假设（H1）：样本1和样本2来自不同的总体分布。

3. KS检验统计量（D）表示两个累积分布函数之间的最大差异。

更确切地说，D表示样本1的CDF与样本2的CDF之间的最大垂直距离。

第二步：KS检验的应用场景KS检验可以广泛应用于以下情况：1. 假设检验：用于判断两个样本是否来自同一总体分布。

2. 模型拟合优度检验：用于评估模型拟合数据的拟合优度。

3. 特征选择：用于选择与特定事件相关联的变量。

第三步：KS检验的假设检验过程下面以假设检验为例，详细介绍KS检验的步骤：1. 收集数据并准备工作：收集两个样本的数据，并对数据进行清洗和准备工作。

2. 计算累积分布函数（CDF）：计算样本1和样本2的累积分布函数。

3. 比较两个CDF：将样本1的CDF和样本2的CDF进行比较，并计算它们之间的最大差异（D值）。

4. 设定显著性水平：根据研究的要求，设定显著性水平（一般为0.05或0.01）。

5. 判断结果：若D值较大的话，拒绝零假设，认为两个样本来自不同的总体分布。

若D值较小的话，则无法拒绝零假设，认为两个样本来自同一总体分布。

第四步：KS检验结果的解读KS检验的结果包含了D值和p值两部分：1. D值：D值表示样本1的CDF与样本2的CDF之间的最大垂直距离。

D值越大，说明两个样本之间的差异性越大。

ks检验结果解读-回复什么是KS检验？KS检验，全称为Kolmogorov-Smirnov检验，是一种非参数检测方法，用于检验两个样本是否来自同一个总体分布或者两个总体分布是否有显著差异。

KS检验的原理基于经验分布函数和理论分布函数之间的最大偏离程度的比较，通过计算两个样本的经验分布函数之间的最大差异来判断两个样本之间的差异。

KS检验的假设和原假设在进行KS检验时，需要对两个样本进行假设和原假设的设定。

假设A为第一个样本，假设B为第二个样本。

其假设和原假设分别如下：假设A: 第一个样本满足某一特定分布；假设B: 第二个样本满足某一特定分布；原假设：假设A和假设B满足相同的分布。

如何进行KS检验？进行KS检验的步骤如下：1. 设置显著性水平α。

通常情况下，α取0.05或0.01。

2. 将两个样本按照大小顺序排列。

3. 计算每个样本的累积频率，即每个数值出现的相对频率。

4. 计算两个样本的经验分布函数。

5. 计算两个样本在每个数值处的差异绝对值。

6. 找到两个样本在所有数值上最大的差异值。

7. 根据显著性水平α，查表或计算得到临界值。

若计算得到的最大差异值大于临界值，则拒绝原假设，认为两个样本来自不同的分布；若最大差异值小于临界值，则接受原假设，认为两个样本来自相同的分布。

KS检验的结果解读在进行KS检验后，我们会得到一个统计量和一个p值。

统计量是两个样本在每个数值上的最大差异值，p值是根据统计量和样本量计算得到的概率。

当p值小于显著性水平α时，我们拒绝原假设，认为两个样本来自不同的分布；当p值大于显著性水平α时，我们接受原假设，认为两个样本来自相同的分布。

需要注意的是，p值是一个概率值，是某一事件发生的概率。

当p值较小时，表示两个样本之间的差异较大，反之则差异较小。

总结KS检验是一种常用的非参数检验方法，用于检验两个样本是否来自相同的总体分布。

在进行KS检验时，首先设置显著性水平α，然后按照一定的步骤计算出统计量和p值，最后根据p值来进行结果的解读。

ks检验结果解读-回复KS检验结果解读KS检验，又称为Kolmogorov-Smirnov检验，是一种非参数检验方法，用于比较两组数据的累积分布函数（CDF）。

它可以用来确定两组数据之间是否有显著差异。

在统计学领域被广泛应用于样本的分布形态比较、模型拟合优度检验和时间序列检验等方面。

KS检验的原理基于两组数据的累积分布函数的差异。

该方法通过计算两组数据的经验分布函数，即将数据按照从小到大的顺序排列，并以每一个数据点为横坐标，以该数据点之前的数据个数除以总数据个数为纵坐标，画出的曲线即为经验分布函数。

KS检验通过比较两组数据的经验分布函数，得到两组数据之间的最大差异值D。

D的计算公式为：D=maxF1(x)-F2(x) ，其中F1(x)和F2(x)分别表示两组数据的经验分布函数。

在进行KS检验时，我们首先需要设置一个显著性水平（一般为0.05）。

如果计算得到的D值大于对应的临界值，我们就可以拒绝原假设，即认为两组数据在累积分布函数上存在显著差异。

临界值可以通过查找KS检验的临界值表或使用统计软件进行计算得到。

KS检验不仅可以用于两组数据之间的比较，还可以用于单组数据的拟合优度检验。

在进行拟合优度检验时，我们需要先选定一个理论分布，然后将该分布的累积分布函数与我们的样本数据进行比较。

如果计算得到的D 值小于对应的临界值，我们就无法拒绝原假设，即认为样本数据与理论分布之间存在拟合优度。

而对于KS检验结果的解读，我们可以按照以下步骤进行：1. 确定原假设和备择假设：在进行KS检验之前，我们首先需要确定原假设和备择假设。

原假设通常为两组数据或样本数据与理论分布之间没有显著差异，备择假设为存在显著差异。

2. 计算D值和临界值：根据两组数据或样本数据的经验分布函数，计算出D值并确定对应的临界值。

通过比较D值和临界值的大小，我们可以判断两组数据是否存在显著差异。

3. 解释结果：如果计算得到的D值大于临界值，我们可以拒绝原假设，认为两组数据存在显著差异。

ks检验结果解读-回复KS检验是一种常用的统计方法，用于比较两个样本或一个样本与总体的差异是否显著。

在本文中，我们将详细解读KS检验的结果，并一步一步回答与之相关的问题。

一、KS检验的基本原理KS检验全称为Kolmogorov-Smirnov检验，是一种非参数检验方法。

它的基本原理是通过比较两个累积分布函数之间的最大差值来判断两个样本是否来自同一个总体或一个样本与总体之间的差异是否显著。

这里的累积分布函数是指比原随机变量小于等于某个特定值的概率。

二、KS检验的假设检验KS检验通常有两个假设要进行检验：零假设(H0)和备择假设(H1)。

1. 零假设(H0)：样本或两个样本来自同一个总体，或一个样本与总体之间没有显著差异。

2. 备择假设(H1)：样本或两个样本来自不同的总体，或一个样本与总体之间存在显著差异。

三、KS检验结果的解读KS检验的结果通常是一个p值，它表示在零假设成立的情况下，观察到当前样本或两个样本之间的差异出现的概率。

p值小于设定的显著性水平（通常是0.05）时，就可以拒绝零假设，接受备择假设，即认为样本或两个样本来自不同的总体，或一个样本与总体之间存在显著差异。

反之，当p值大于显著性水平时，无法拒绝零假设，即无法认为样本或两个样本来自不同的总体，或一个样本与总体之间存在显著差异。

四、如何进行KS检验进行KS检验的一般步骤如下：1. 假设零假设成立，计算两个样本或一个样本与总体的累积分布函数。

2. 计算两个累积分布函数之间的最大差值，即KS统计量。

3. 根据样本量和显著性水平，查表或使用统计软件得到对应的临界值。

4. 对比KS统计量和临界值，若KS统计量大于临界值，则拒绝零假设；否则，接受零假设。

五、KS检验结果解读示例为了更好地理解KS检验的结果解读，我们将以一个示例来说明。

假设我们要比较两个样本A和B的分布是否相同，执行KS检验后得到的结果为p值=0.03。

显著性水平设定为0.05。

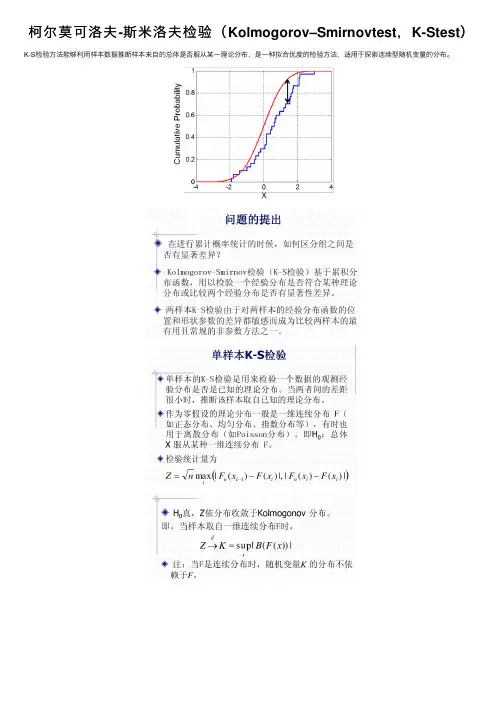
柯尔莫可洛夫-斯⽶洛夫检验（Kolmogorov–Smirnovtest，K-Stest）K-S检验⽅法能够利⽤样本数据推断样本来⾃的总体是否服从某⼀理论分布，是⼀种拟合优度的检验⽅法，适⽤于探索连续型随机变量的分布。

Kolmogorov–Smirnov testKolmogorov–Smirnov statistic累计分布函数：定义n 个独⽴同分布（i.i.d.）有序观测样本Xi 的经验分布函数Fn 为：样本集Xi的累计分布函数F n(x)sup x是距离的上确界()，基于Glivenko–Cantelli theorem（），若Xi服从理论分布F(x)，则当n趋于⽆穷时Dn⼏乎肯定（）收敛于0。

Kolmogorov通过有效地提供其收敛速度加强了这⼀结果。

Donsker定理（）提供了⼀个更强的结果。

在实践中，统计量需要相对⼤量的数据点(与 statistic等其他拟合优度标准相⽐)才能恰当地拒绝零假设。

Kolmogorov distribution预备知识：(1) 独⽴增量过程顾名思义，就是指其增量是相互独⽴的。

严格定义如下：(2) 维纳过程（Wiener process）⼤概可以理解为⼀种数学化的布朗运动，严格定义如下：(3)布朗桥（Brownian bridge）⼀种特殊的维纳过程，严格定义如下：⼀个在[0,T]区间上，且WT=0的维纳过程。

红⾊和绿⾊的都是“布朗桥”。

Kolmogorov distribution柯尔莫⼽罗夫分布是随机变量K的分布:即是通过求布朗运动上确界得到的随机变量的分布。

其中B(t)为布朗桥。

它的累积分布函数可以写为：which can also be expressed by the . Both the form of the Kolmogorov–Smirnov test statistic and its asymptotic distribution under the null hypothesis were published by , while a table of the distribution was published by . Recurrence relations for the distribution of the test statistic in finite samples are available.单样本Kolmogorov Goodness-of-Fit Test单样本K-S检验即是检验样本数据点是否满⾜某种理论分布。

单样本ks检验原理
ks检验，又称为卡方检验，是一种应用于比较两个统计分布或两个指标之间差异的检验统计方法，其基本原理是计算两个样本的累积分布的最大距离，称为ks距离，从而来判断样本是否有显著的差别。

以单样本检验为例，单样本ks检验的假设检验原理为：将一个单样本的所有的观测值按照大小顺序排列出来，对应有一个累积分布函数，即第i个观测值对应的累积分布值为F(xi)，首先要满足正态分布假定，即该单样本观测值应满足正太分布，如果满足正态分布，则该样本累积分布应满足标准正态分布函数，如果不满足标准正态分布函数，则说明这个样本不满足检验条件，此时ks检验不能使用；若用样本累积分布函数F(x)替代标准正态分布函数，以得到样本的累积分布函数，此时，计算两个累积分布函数的最大距离，如果最大距离大于某个显著性水平的阈值，则说明该样本与标准正态分布有显著的差别；若最大距离小于阈值，则说明该样本与标准正态分布没有显著的差别。

KS-检验（Kolmogorov-Smirnovtest）Kolmogorov-Smirnov是⽐较⼀个频率分布f(x)与理论分布g(x)或者两个观测值分布的检验⽅法。

其原假设H0:两个数据分布⼀致或者数据符合理论分布。

D=max| f(x)- g(x)|，当实际观测值D>D(n,α)则拒绝H0，否则则接受H0假设。

KS检验与t-检验之类的其他⽅法不同是KS检验不需要知道数据的分布情况，可以算是⼀种⾮参数检验⽅法。

当然这样⽅便的代价就是当检验的数据分布符合特定的分布事，KS检验的灵敏度没有相应的检验来的⾼。

在样本量⽐较⼩的时候，KS检验最为⾮参数检验在分析两组数据之间是否不同时相当常⽤。

PS：t-检验的假设是检验的数据满⾜正态分布，否则对于⼩样本不满⾜正态分布的数据⽤t-检验就会造成较⼤的偏差，虽然对于⼤样本不满⾜正态分布的数据⽽⾔t-检验还是相当精确有效的⼿段。

KS检验是如何⼯作的？1. ⾸先观察下分析数据对于以下两组数据：controlB={1.26, 0.34, 0.70, 1.75, 50.57, 1.55, 0.08, 0.42, 0.50, 3.20, 0.15, 0.49, 0.95, 0.24, 1.37, 0.17, 6.98, 0.10, 0.94, 0.38}treatmentB= {2.37, 2.16, 14.82, 1.73, 41.04, 0.23, 1.32, 2.91, 39.41, 0.11, 27.44, 4.51, 0.51, 4.50, 0.18, 14.68, 4.66, 1.30, 2.06, 1.19}对于controlB，这些数据的统计描述如下：Mean = 3.61Median = 0.60High = 50.6 Low = 0.08Standard Deviation = 11.2可以发现这组数据并不符合正态分布，否则⼤约有15%的数据会⼩于均值-标准差（3.61-11.2），⽽数据中显然没有⼩于0的数。

第四节Kolmogorov-Sirmov单样本检验一、Kolmogorov-Sirmow单样本检验Kolmogorov-Sirmov单样本检验是一种拟合优度性检验。

它的基本原理同Chi-Square检验，但比Chi-Square检验更为精确。

K-S检验是将一组样本值(观察结果)的分布和某一指定的理论分布函数（如正态分布，均匀分布，泊松分布，指数分布）进行比较，确定两者之间的符合程度。

这种检验可以确定是否有理由认为样本的观察结果来自具有该理论分布的总体。

简言之，这种检验包括确定理论分布下的累积频数分布，以及把这种累积频数分布和观察的累积频数分布进行比较(这里的理论分布系指零假设成立时所预期的分布)，确定理论分布和观察分布的最大差异点，参照抽样分布并定出这样大的差异是否基于偶然。

这就是说，若观察的结果的确是从理论分布抽取的随机样本，则抽样分布将指出这种观察到的差异程度是否随机出现的。

1二、Kolmogorov-Sirmov单样本检验方法1．K-S单样本检验步骤（1）在数据输入之后，依次单击Analyze→Nonparametric Tests→ 1-Sample K-S →打开One-Sample Kolmogorov-Sirmov Test对话框；（2）在原变量栏选择所要检验的分布到Test Variable List栏；（3）在Test Distribution栏选择理论分布函数复选项：●Normal复选项：如选择此项，则检验变量是否服从正态分布，系统默认；●Uniform复选项：如选择此项，则检验变量是否服从均匀分布；●Poisson复选项：如选择此项，则检验变量是否服从泊松分布；●Exponential复选项：如选择此项，则检验变量是否服从指数分布。

（4）单击“Option”按钮，打开Options对话框：●Statistics栏：在此栏可选择Descriptive复选项，则会输出观测的均值、最小值、最大值、标准差等描述统计；选择Quartiles复选项：则输出观测的四分之一分位数、二分之一分位数和四分之三分位数。