2011年电子科技大学836信号与系统和数字电路真题和答案
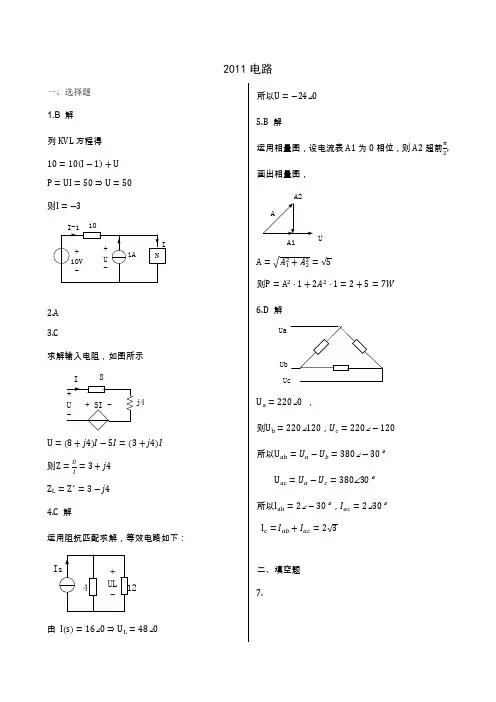
- 格式:pdf
- 大小:685.54 KB
- 文档页数:9

电子科技大学2010 -2011学年第二学期期末考试 A 卷课程名称:_数字逻辑设计及应用__ 考试形式:闭卷考试日期:20 11 年7 月7 日考试时长:_120___分钟课程成绩构成:平时30 %,期中30 %,实验0 %,期末40 %本试卷试题由__六___部分构成,共__6___页。
I. Fill your answers in the blanks(2’ X 10=20’)1. A parity circuit with N inputs need N-1XOR gate s. If the number of “1” in an N logic variables set, such as A、B、C、…W, is even number, then__________A B C W⊕⊕⊕⋅⋅⋅⋅⊕=0 .2. A circuit with 4 flip-flops can store 4bit binary numbers, that is, include 16 states at most.3. A modulo-20 counter circuit needs 5 D filp-flops at least. A modulo-288 counter circuit needs 3 4-bit counters of 74x163 at least.4. A 8-bit ring counter has 8 normal states. If we want to realize the same number normal states, we need a 4bit twisted-ring counter.5. If the input is 10000000 of an 8 bit DAC, the corresponding output is 5v. Then an input is 00000001 to the DAC, the corresponding output is 5/128 (0.0391) V; if an input is 10001000, the corresponding DAC output is 5.3125V.II. Please select the only one correct answer in the following questions.(2’ X 5=10)B ) chips of 4K ⨯4 bits RAM to form a 16 K ⨯ 8 bits RAM.A) 2 B) 8 C) 4 D) 162. To design a "01101100" serial sequence generator by shift registers, we need a( A)-bit shift register as least.A) 5 B) 4 C) 3 D) 63. For the following latches or flip-flops, ( B) can be used to form shift register.A) S-R latch B) master-slave flip-flop C) S-R latch with enable D) S’-R’ latch4. Which of the following statements is correct? ( C )A) The outputs of a Moore machine depend on inputs as well as the states.B) The outputs of a Mealy machine depend only on the states.C) The outputs of a Mealy machine depend on inputs as well as the states. D) A), B), C) are wrong.5. There is a state/output table of a sequential machine as the table 1, what the input sequences isdetected? ( D )A) 11110 B) 11010 C) 10010 D) 10110Table 1III.Analyze the sequential-circuit as shown in figure 1. [15’]1. Write out the excitation equations, transitionequations and output equation. [5’]2. Assume the initial state is Q 2Q 1=00, complete thetiming diagram for Q 2 ,Q 1 and Z.( Don ’t need consider propagation delay of each component)[10’]Figure-1解答:激励方程: D 1=Q 1⊕Q 2,D 2= Q /1+ Q /2转移方程:Q 1 *= D 1=Q 1⊕Q 2,Q 2 *=D 2= Q /1+ Q /2 输出方程:Z= Q 1•Q 2IV. Design a Mealy sequential detector with one input x and one output z. If and only if xdescribe the state meaning and finish the state/output table. [15] Example : x :0 1 0 1 1 1 1 0 0 1 1 0 0 1 1 1 1 1 z :0 0 0 0 0 0 1 0 0 1 0 0 0 1 0 0 1 1XState meaningS 0 1 Initial A A,0 B,0 Received 1 B C,0 D,0 Received 10 C E,0 B,0 Received 11 D C,0 F,0 Received 100 E A,0 B,1 Received 111 F C,0F,1S*,ZV. Analyze the circuit as shown below, which contains a 74x163 4-bit binary counter, a 74x138[15’] ’ output F. [5’]2. Write out the sequence of states for the 74x161 in the circuit. [7’]3. Describe the modulus(模) of the circuit. [3’]解答:F=D2=Y6/=(QDQCQBQA /)/ 状态序列:0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,0,1,2,… M=15VI.the state transition sequence is 0→2→4→1→3→0→…with the binary code. 1. Fill out the transition/output table. [8’]2. Write out the excitation equations and output equation. [4’]3. List the complete transition/output table, and check the self-correct. [3’] transition/output table : 74X161的功能表输入 当前状态 下一状态 输出CLR_L LD_L ENT ENP QD QC QB QA QD* QC* QB* QA* RCO 0 X X X X X X X 0 0 0 0 1 0 X X X X X X D C B A 1 1 0 X X X X X QD QC QB QA 1 1 X 0 X X X X QD QC QB QA 1 1 1 1 0 0 0 0 0 0 0 1 1 1 1 1 0 0 0 1 0 0 1 0 1 1 1 1 0 0 1 0 0 0 1 1 1 1 1 1 0 0 1 1 0 1 0 0complete transition/output table:输出方程:Z=Q1Q0检查自启动:当Q2Q1Q0=101,可得下一状态为001;当Q2Q1Q0=110,可得下一状态为101;当Q2Q1Q0=111,可得下一状态为001。

电子科大模电期末真题10~11学院___________________ 系别____________ 班次_____________ 学号__________ 姓名________________………….……密…..……….封……..……线………..…以………..…内………....答…………...题…………..无…….….效…..………………..电子科技大学二零一零至二零一一学年第 1 学期期末考试模拟电路基础课程考试题A卷(120 分钟)考试形式:开卷考试日期2011年1 月 5 日课程成绩构成:平时20 分,期中20 分,实验0 分,期末60 分一二三四五六七八九十合计复核人签名得分签名一、填空题(共30分,共 15个空格,每个空格2 分)1、共发射极放大器(NPN管),若静态工作点设置偏高,可能产生_饱和__失真,此时集电极电流会出现__上___(上、下)削峰失真。
2、某晶体管的极限参数P CM = 200 mW,I CM = 100 mA,U(BR)CEO = 30 V,若它的工作电压U CE为10 V,则工作电流不得超过20 mA;若工作电流I C = 1 mA,则工作电压不得超过30 V。
4、电路及直流测试结果如图1所示,分别指出它们工作在下列三个区中的哪一个区(恒流区、夹断区、可变电阻区)。
得图1(a) 恒流区 ; (b) 可变电阻区 。
5、由三端集成稳压器构成的直流稳压电路如图2所示。
已知W7805的输出电压为5V ,I Q =10 mA ,晶体管的β=50,|U BE |=0.7 V ,电路的输入电压U I =16 V ,三极管处于放大 (放大,饱和,截止)状态, R 1上的电压为 5.7 V ,输出电压U o 为 9 V 。
图26、设图3中A 均为理想运放,请求出各电路的输出电压值。
U 01= 6 V; U 02= 6 V; U 03= 4 V; U 04= 10 V; U 05= 2 V; U 06= 2 V 。

电子科技大学二零零九年至二零一零学年第二学期“数字逻辑设计及应用”课程考试题(半期)(120分钟)考试日期2011年4月23日一二三四五六七八九十总分评卷教师I. To fill the answers in the “( )” (2’ X 19=38)1. [1776 ]8 = ( 3FE )16 = ( 1111111110 )2= ( 1000000001 ) Gray .2. (365)10 = ( 001101100101 )8421BCD=( 001111001011 ) 2421 BCD.3.Given an 12-bit binary number N. if the integer’s part is 9 bits and the fraction’s part is 3 bits ( N = a8 a7 a6 a5 a4 a3 a2 a1 a0 . a-1 a-2 a-3), then the maximum decimal number it can represent is ( 511.875 ); the smallest non-zero decimal number it can represent is ( 0.125 ).4. If X’s signed-magnitude representation X SM is(110101)2, then it’s 8-bit two’s complement representation X2’s COMP is( 11101011 ) , and (–X)’s 8-bit complement representation (–X) 2’s COMP is ( 00010101 )2 .5. If there are 2011 different states, we need at least ( 11 ) bits binary code to represent them.6.If a positive logic function expression is F=AC’+B’C(D+E),then the negative logic function expression F = ( (A+C’)(B’+(C+DE)) ).7. A particular Schmitt-trigger inverter has V ILmax = 0.7 V, V IHmin = 2.1 V, V T+= 1.7 V, and V T-= 1.3 V, V OLmax=0.3V, V OHmin=2.7V. Then the DC noise margin in the HIGH state is ( 0.6V ), the hysteresis is ( 0.4V ). 8.The unused CMOS NAND gate input in Fig. 1 should be tied to logic ( 1 ).Fig.1Circuit of problem I-89. If number [ A ] two’s-complement =11011001and [ B] two’s-complement=10011101 , calculate[-A-B ]two’s-complement, [-A+B ]two’s-complement and indicate whether or not overflow occurs.[-A-B ] two’s-complement=[ 10001010 ], overflow: [ yes ][-A+B ] two’s-complement=[ 11000100 ], overflow: [ no ].10.The following logic diagram Fig.2 implements a function of 3-variable with a 74138. The logic function can be expressed as F (A,B,C) = ∑A,B,C ( 0,1,2 ).Fig.2 Circuit of problem I-10II. There is only one correct answer in the following questions.(3’ X 9 = 27)1. Which of the following Boolean equations is NOT correct? ( B )A) A+0=A B) A1 = AC) D)2. Suppose A2’s COMP =(1011),B2’s COMP =(1010),C2’s COMP =(0010). In the following equations, the most unlikely to produce overflow is( C )。


西安电子科技大学《电路、信号与系统》真题2011年(总分:75.00,做题时间:90分钟)一、{{B}}{{/B}}(总题数:6,分数:24.00)1.T等于______。
∙ A.20s∙ B.40s∙ C.60s∙ D.120s(分数:4.00)A.B.C. √D.解析:[解析] [*],f(k)的周期T为T1、T2、T3的最小公倍数,即为60s。
2.-τδ"(τ)dτ等于______。
∙ A.δ(t)+u(t)∙ B.δ(t)+δ'(t)∙ C.δ'(t)+2δ(t)+u(t)∙ D.δ'(t)(分数:4.00)A.B.C. √D.解析:[解析] [*]3.卷积积分(t+1)u(t+1)*δ'(t-2)等于______。
∙ A.δ(t-1)∙ B.u(t-1)∙ C.δ(t-3)∙ D.u(t-3)(分数:4.00)A.B. √C.D.解析:[解析] 原式=tu(t)*δ'(t-1)=[tu(t)]'*δ(t-1)=u(t)*δ(t-1)=u(t-1)。
4.______。
∙ A.1∙ B.0.5π∙ C.π∙ D.2π(分数:4.00)A.B. √C.D.解析:[解析] 根据傅里叶变换定义式,有F(jω)=[*]f(t)e-jωt dt,则:[*]根据常用傅里叶变换,可知Sa(t)[*]F(jω)=πG2(ω)。
所以:[*]5.因果信号f(k)F(z)的收敛域为______。
∙ A.|z|>2∙ B.|z|>1∙ C.|z|<1∙ D.1<|z|<2(分数:4.00)A. √B.C.D.解析:[解析] 离散系统因果信号收敛域为|z|>a,非因果信号收敛域为|z|<b,因为F(z)=[*]的极点为p1=-1,P2=2。
所以,当|z|<1时,则f(k)为非因果信号;当1<|z|<2时,则f(k)为因果信号及非因果信号两部分;当|z|>2时,则f(k)为因果信号。

信号与系统习题解答11.1 用代数式表达下列复数:已知形式为θj re ,要求表达形式为jy x +,采用公式:θcos r x =,θsin r y =。
解: 2121-=πj e 2121-=-πj ej e j =2π j e j -=-2πj ej=25πj ej+=124π j ej+=1249πj ej -=-1249π j ej-=-124π1.2 用极式表达下列复数:已知形式为jy x +,要求表达形式为θj re ,采用公式:22y x r +=,()πθπθ≤<-=-xytg 1。
解:055j e = πj e 22=- 233πjej -=-()2242221ππjj e e j --=⎪⎪⎭⎫ ⎝⎛=- ()442221πππjjje eej j =⋅=--2442211πππjjje ee jj ==-+-1234223122πππjj je e ej j -==++1.54 (a )证明表达式 ⎪⎩⎪⎨⎧≠--==∑-=111110αααααN N n nN证: 因为 1=α 时,1=n α (n 为任意值时)所以,1=α 时,N N n n =∑-=10α因为 ()()NN ααααα-=++++--1 (111)2所以,当1≠α时,()ααααα--=++++-11 (11)2NN 原式得证。
(b) 证明:1<α时,αα-=∑∞=110n n 证:因为 1<α时,0lim ==∞→NN α所以:αααα-=--=∞→∞=∑1111lim 0N N n n(c )证明:1<α时,()21ααα-=∑∞=n nn 证:令()αααf n n=-=∑∞=11为α的连续函数对上式进行微分运算可得:()()2111αααα-==∑∞=-n n n d df 同时乘以α就可以得到:()21αααααα-==∑∞=n nn d df (d )当1<α时,计算?=∑∞=kn nα解: 因为∑∑∑∞=-=∞=+=kn nk n n n n ααα100所以:αααααααα-=----=-=∑∑∑-=∞=∞=1111110kk k n nn nk n n1.55 计算下列和式,采用代数式表达。


………密………封………线………以………内………答………题………无………效……电子科技大学二零 一 一 至二零 一 二 学年第 一 学期期 中 考试SIGNALS AND SYSTEMS 课程考试题 卷 ( 120 分钟) 考试形式: 闭卷 考试日期 20 11 年 月 日课程成绩构成:平时 10 分, 期中 20 分, 实验 10 分, 期末 60 分1(56points).Each of the following questions may have one or two right answers, justify your answers and write it in the blank. (1)()cos 221πδ+∞-∞-=⎰t t dt ( d ).(a) 1 (b) -1 (c) 0.5 (d) -0.5(2) The fundamental period of the signal []23cos sin 32ππ⎡⎤⎡⎤=-⎢⎥⎢⎥⎣⎦⎣⎦x n n n is ( a ). (a) 12N = (b) 6N = (c) 8N = (d) 24N = (3) Let ()1tx t e -= and ()()()14k x t x t t k δ+∞=-∞=*-∑. The Fourier series coefficients of ()x t may be ( a ).(a) {} and Im 0-==k k k a a a (b) {} and Im 0-=-=k k k a a a (c) {} and Re 0-==k k k a a a (d) {} and Re 0k k k a a a -=-=(4) Consider an LTI system with unit impulse response ()h t illustrated in Figure 1, if the input is ()()d t x t dtδ=, the output () 0.5t y t =- is( b ).(a) -1 (b) 1 (c) -0.5 (d) 0.5(5) The convolution integral ()222t te e u t -*=( c ).(a) 2 (b)214te (c)212te (d)()212te u t(6) Which of the following systems is an linear system ( a ). In each example, []y n denotes the system output and []x n is the systeminput.(a) [][][]cos y n n x n = (b) [][]{}cos 3y n x n = (c) [][]()ln y n x n = (d) [][]2y n x n =(7) Which of the following systems are causal and stable system ( ad ). In each example, ()h t denotes the impulse response of thefollowing systems.(a) ()()()13h t t t δδ=-+- (b) ()()()0.5cos 2t h t t e u t =- (c) ()()()13h t t t δδ=+++ (d) ()()()cos 2t h t t e u t -=-(8) Determine the following signals which have finite total energy ( bc ). (a) []()[]1x n n u n =+ (b) ()()23tx t eu t -=+(c) []()[]1cos /32nx n n u n π⎛⎫= ⎪⎝⎭(d) () , tx t e t =-∞<<+∞tFigure 1………密………封………线………以………内………答………题………无………效……(9) Consider a continuous-time LTI system whose frequency response is ()()sin /2Hj ωωω=. If we know the output ()y t to some periodicinput signals are ()0y t =. The fundamental period of the input signal may be ( ac ). (a) 1T = (b) 2T = (c) 0.5T = (d) 3T =2(12points). A continuous-time signal ()32-+x t is illustrated in Figure 2.(a) Determine the signal ()x t . (b) Sketch and label carefully ()x t .3(10 points).Consider an LTI system whose response to the signal ()t x 1 in Figure 3 is the signal ()t y 1 illustrated in Figure 4. Determine the response of the system to the input ()t x 2 depicted in Figure 5 .4(12 points). Consider a continuous-time LTI system whose frequency response ()H j ω is illustrated in Figure 6. If the input signal()1cos 3sin 6ππ=++x t t t , determine the output of the system.12Figure 3ωFigure 6tFigure 2………密………封………线………以………内………答………题………无………效……14(10points). Consider an LTI system whose input []x n and unit impulse response []h n are given by []{}1,0,1,1,0,1x n n =-=-,[]{}2,1,3,2,2,3,4,5h n n ==. Determine the output [][][]n h n x n y *= of this system.《信号与系统》半期考试评分标准说明1.填空题(56分)⑴. (d) ⑵ (a) ⑶ (a) ⑷ (b) ⑸ (c) ⑹ (a) ⑺ (ad) ⑻ (bc) ⑼ (ac) ⑽ (ab) 本部分评分规则:1) 选择题共14个正确答案,1-6题为单选,7-10题为双选; 2) 若只填写了1个答案,正确得4分,错误得0分;3) 若填写了2个答案,2个正确得8分,1个正确、1个错误得4分,2个错误得0分;4) 若填写了3个答案,2个正确、1个错误得4分,1个正确、2个错误得2分,3个错误得0分; 5) 若填写了4个答案,得0分。


831“电路、信号与系统”复习参考提纲总体要求一、总体要求“电路、信号与系统”由“电路”(80分)和“信号与系统”(70分)两部分组成。
“电路”要求学生掌握电路的基本理论和基本的分析方法,使学生具备基本的电路分析、求解、应用能力。
要求掌握电路的基本概念、基本元件的伏安关系、基本定律、等效法的基本概念;掌握电阻电路的基本理论和基本分析方法;掌握动态电路的基本理论,一阶动态电路的时域分析方法;正弦稳态电路的基本概念和分析方法;掌握谐振电路和二端口电路的基本分析方法。
“信号与系统”要求学生掌握连续信号的时域、频域、复频域分解的数学方法和分析方法,理解其物理含义及特性。
掌握离散信号的时域时域、Z域分解的数学方法和分析方法,理解其物理含义及特性。
熟练掌握时域中的卷积运算和变换域中的傅里叶变换、拉普拉斯变换、Z变换等数学工具。
掌握系统函数及系统性能的相关概念及其判定方法。
掌握线性系统的状态变量分析法。
研究生课程考试是所学知识的总结性考试,考试水平应达到或超过本科专业相应的课程要求水平。
各章复习要点部分各章复习要点二、“电路”部分电路”各章复习要点(一)电路基本概念和定律1.复习内容电路模型与基本变量,基尔霍夫定律,电阻元件与元件伏安关系,电路等效的基本概念2.具体要求*电路模型与基本变量***电压、电流及其参考方向的概念、电功率、能量的计算***基尔霍夫定律***电阻元件及欧姆定律;***电压源、电流源及受控源概念;**等效初步概念,掌握串、并联电阻电路的计算,实际电源两种模型及其等效互换(二)电阻电路分析1.复习内容电路的方程分析法,网孔法和回路法,节点法和割集法。
电路定理的概念、条件、内容和应用。
2.具体要求*支路分析法***网孔分析法;***节点分析法***叠加定理,替代定理原理及应用***戴维南定理、诺顿定理和分析方法***最大功率传输定理**互易定理和特勒根定理(三)动态电路1.复习内容动态元件的概念,动态元件的伏安关系。
西安电子科技大学《信号、电路与系统》考研真题2011年(总分:75.00,做题时间:90分钟)一、{{B}}选择题{{/B}}(总题数:6,分数:24.00)1.如图所示电路,如1A电流源产生功率为50W,则元件N上电流I为______。
∙ A.3A∙ B.-3A∙ C.5A∙ D.-5A(分数:4.00)A.B. √C.D.解析:[解析] 求解电路如图所示,由题可得知电流源两端电压:[*]根据KVL定理,可得10Q电阻电压为:[*]则元件N上的电流为:I=4+1=-3A [*]2.如图所示电路,ab端等效电容C ab等于______。
∙ A.40μF∙ B.50μF∙ C.10μF∙ D.110μF(分数:4.00)A. √B.C.D.解析:[解析] 电容串并联的等效容值计算公式如下:C1串[*];C1并[*]。
利用该特性对图示电路依次进行等效解析如下:20μF与20μF串联,得10μF;10μF与50μF并联,得60μF;60μF与30μF串联,得20μF;20μF与20μF并联,得40μF。
3.如图所示电路,负载阻抗Z L为多大时吸收最大功率?______∙ A.8-j4Ω∙ B.8+j4Ω∙ C.3-j4Ω∙ D.3+j4Ω(分数:4.00)A.B.C. √D.解析:[解析] 求戴维南等效。
开路电压:[*]短路电流[*],所以:Z eq=3+j4Ω根据最大功率传输定理的阻抗匹配,匹配阻抗为等效阻抗的共轭,即Z L=(3+j4)*=3-j4时,Z L吸收最大功率。
4.如图所示电路,,则电压为______。
∙ A.6∠0°V∙ B.12∠0°V∙ C.24∠0°V∙ D.48∠0°V(分数:4.00)A.B.C. √D.解析:[解析] 求解电路如图所示,原边线圈电流为i2,副边线圈的电流i1,根据理想变压器的特性,可知[*]。
[*]在副边电路有[*],原边电路等效电压为[*]。
[历年试题] 电子科技大学2011年信号系统面试题[复制链接]潇亦然潇亦然当前离线注册时间2011-1-3最后登录2011-7-13在线时间47 小时阅读权限255积分23223帖子1037精华5UID193753管理员在线时间47 小时弘豆1111 最后登录2011-7-13积分23223精华5帖子1037串个门加好友打招呼发消息电梯直达1#发表于2011-5-8 15:21:01 |只看该作者|倒序浏览本帖隐藏的内容第1章信号与系统的基本概念1.信号、信息与消息的差别?信号:随时间变化的物理量;消息:待传送的一种以收发双方事先约定的方式组成的符号,如语言、文字、图像、数据等信息:所接收到的未知内容的消息,即传输的信号是带有信息的。
2.什么是奇异信号?函数本身有不连续点或其导数或积分有不连续点的这类函数统称为奇异信号或奇异函数。
例如:单边指数信号(在t=0点时,不连续),单边正弦信号(在t =0时的一阶导函数不连续)。
较为重要的两种奇异信号是单位冲激信号d(t)和单位阶跃信号u(t)。
5.线性时不变系统:同时满足叠加性和均匀性以及时不变特性的系统线性时不变系统对信号的处理作用可以用冲激响应(或单位脉冲响应)、系统函数或频率响应进行描述。
而且多个系统可以以不同的方式进行连接,基本的连接方式为:级联和并联。
第2章连续时间系统的时域分析1.如何获得系统的数学模型?数学模型是实际系统分析的一种重要手段,广泛应用于各种类型系统的分析和控制之中。
不同的系统,其数学模型可能具有不同的形式和特点。
对于线性时不变系统,其数学模型通常由两种形式:建立输入-输出信号之间关系的一个方程或建立系统状态转换的若干个方程组成的方程组(状态方程)。
对于本课程研究较多的电类系统而言,建立系统数学模型主要依据两个约束特性:元件特性约束和网络拓扑约束。
一般地,对于线性时不变连续时间系统,其输入-输出方程是一个高阶线性常系数微分方程,而状态方程则是一阶常系数微分方程组。
图1一、填空题1.五个变量构成的所有最小项之和等于 ( )。
2.已知某数的二进制原码表示为 ( 110110) 2 , 则其对应的8-bit 补码表示为 ( )2。
3.已知∑=CB A F ,,)3,0(,则∑='C B A F ,,( )。
4.要使D 触发器按'*Q Q =工作,则D 触发器的输入D=( )。
5.用移位寄存器产生1101010序列,至少需要( )位的移位寄存器。
二、单项选择题:1. 若要将一异或门当作反相器(非门)使用,则输入端A 、B 端的连接方式是( )。
A. A 或B 中有一个接“0”B. A 或B 中有一个接“1”C. A 和B 并联使用D. 不能实现 2.组合电路的竞争冒险是由于( )引起的。
A. 电路不是最简B. 电路有多个输出C. 电路中使用不同的门电路D. 电路中存在延时3.某一逻辑函数真值表确定后,下面描述该函数逻辑功能的表达式中,具有唯一性的是( )。
A .该逻辑函数的最简与或式B .该逻辑函数的积之和标准型C .该逻辑函数的最简或与式D .该逻辑函数的和之积式4.若最简状态转换表中,状态数为n ,则所需状态变量数K 为 ( )的整数.A .n K 2log =B .n K 2log <C . n K 2log ≥D . n K 2log ≤5.某计数器的状态转换图如图1所示,其该计数器的模为( )。
A . 八 B. 五 C. 四 D. 三三、 组合电路分析:1.求逻辑函数 Z Y X Y X Z X F ⋅'⋅+⋅+⋅'= 的最简积之和表达式。
2.已知逻辑函数∑=ZY X F ,,)7,5,1(, 请写出该函数的标准和(最小项之和)表达式:3.找出逻辑表达式X W Y W F ⋅+'⋅'=对应的电路的所有静态冒险。
四、组合电路设计:1、试用一片三输入八输出译码器74X138和适当的与非门实现函数:∑=Z Y X W F ,,,)15,14,10,6,3(画出电路连接图。
电子科技大学二零零九年至二零一零学年第二学期“数字逻辑设计及应用”课程考试题(半期)(120分钟)考试日期2011年4月23日I. To fill the answers in the “( )”(2’ X 19=38)1. [1776 ]8= ( 3FE)16 = ( 1111111110)2= ( 1000000001) Gray .2. (365)10 = ( 001101100101)8421BCD=( 001111001011) 2421 BCD.3. Given an 12-bit binary number N. if the integer’s part is 9 bits and the fraction’s part is 3 bits ( N = a8 a7 a6a5a4a3a2a1a0 . a-1a-2a-3), then the maximum decimal number it can represent is ( 511.875 ); the smallest non-zero decimal number it can represent is ( 0.125).4.If X’s signed-magnitude representation X SM is(110101)2, then it’s 8-bit two’s complement representation X2’s COMP is( 11101011 ) , and (–X)’s 8-bit complement representation (–X) 2’sis ( 00010101 )2 .COMP5. If there are 2011 different states, we need at least ( 11 ) bits binary code to represent them.6.If a positive logic function expression is F=AC’+B’C(D+E),then the negative logic function expression F = ( (A+C’)(B’+(C+DE)) ).7. A particular Schmitt-trigger inverter has V ILmax = 0.7 V, V IHmin = 2.1 V, V T+ = 1.7 V, and V T-= 1.3 V, V OLmax=0.3V, V OHmin=2.7V. Then the DC noise margin in the HIGH state is ( 0.6V), the Arrayhysteresis is ( 0.4V).8.The unused CMOS NAND gate input in Fig. 1 should be tied tologic ( 1 ).Fig.1Circuit of problem I-89. If number [ A ] two’s-complement =11011001and [ B]two’s-complement=10011101 , calculate[-A-B ]two’s-complement, [-A+B ]two’s-complement and indicate whether or not overflow occurs.[-A-B ]two’s-complement=[ 10001010], overflow: [ yes ][-A+B ]two’s-complement=[ 11000100], overflow: [ no].10.The following logic diagram Fig.2 implements a function of 3-variable with a 74138. The logic function can be expressed as F (A,B,C) = ∑A,B,C ( 0,1,2 ).Fig.2 Circuit of problem I-10评分基本标准: 每空1分,错则全扣。