异分母分式加减法习题

专题1.4.3异分母分式的加减（知识讲解）【学习目标】1．让学生进一步熟练掌握求最简公分母的方法．2．能根据异分母分式的加减法则进行计算．3．在学习过程中体会从分数到分式的类比的方法，培养乐于探究、合作学习的习惯．【知识梳理】知识模块一异分母分式的加减法归纳：类似地，异分母的分式相加减时，要先通分，即把各个分式的分子、分母同乘一个适当的整式，化成同分母分式，然后再加减．异分母的分式加减法步骤：(1)确定最简公分母；(2)通分(即将各分式的分子分母各乘一个适当的式子，化成同分母分式)；(3)利用同分母的分式加减法则(即分母不变，分子相加减)计算；(4)最后结果要化成最简分式．知识模块二整式与分式的加减运算方法总结：对于一般的分式混合运算来讲，其运算顺序与整式混合运算一样，是先乘方，再乘除，最后算加减，如果遇到括号要先算括号里面的．在此基础上，有时也应该根据具体问题的特点，灵活应变，注意方法．【典型例题】【类型一】分母是单项式例1.计算：(1)32x －13y； (2)1a－12ab＋abc.解析：(1)小题的最简公分母是6xy，(2)小题的最简公分母是2abc，通分后再根据同分母分式相加减的法则进行计算．解：(1)32x－13y＝9y6xy－2x6xy＝9y－2x6xy；(2)1a－12ab＋abc＝2bc2abc－c2abc＋2a22abc＝2bc－c＋2a22abc.方法总结：异分母分式相加减，先通分，再转化为同分母分式相加减．【类型二】 分母是多项式例2. 计算：(1)xx 2－4－2x 2＋4x ＋4； (2)a 2－4a ＋2＋a ＋2； (3)m m －n －n m ＋n ＋2mn m 2－n 2. 解析：依据分式的加减法法则，(1)、(3)中先找出最简公分母分别为(x －2)(x ＋2)2、(m ＋n )(m －n )，再通分，然后运用同分母分式加减法法则运算；(2)中把后面的加数a ＋2看成分母为1的式子进行通分．解：(1)原式＝x （x ＋2）（x －2）－2（x ＋2）2＝x （x ＋2）（x ＋2）2（x －2）－2（x －2）（x ＋2）2（x －2）＝x （x ＋2）－2（x －2）（x ＋2）2（x －2）＝x 2＋4（x ＋2）2（x －2）； (2)原式＝a 2－4＋（a ＋2）2a ＋2＝2a （a ＋2）a ＋2＝2a ； (3)原式＝m （m ＋n ）（m ＋n ）（m －n ）－n （m －n ）（m ＋n ）（m －n ）＋2mn （m ＋n ）（m －n ）＝m 2＋2mn ＋n 2（m ＋n ）（m －n ）＝m ＋n m －n. 方法总结：分母是多项式时，应先因式分解，目的是为了找最简公分母以便通分．对于整式与分式的加减运算，可以将整式的每一项的分母看成1，再通分，也可以把整式的分母整体看成1，再进行通分运算．【类型三】分式的混合运算例3.计算：(1)(x 2－4x ＋4x 2－4－x x ＋2)÷x －1x ＋2； (2)a －52a －6÷(16a －3－a －3)． 解：(1)原式＝[（x －2）2（x －2）（x ＋2）－x x ＋2]÷x －1x ＋2＝(x －2x ＋2－x x ＋2)÷x －1x ＋2＝－2x ＋2×x ＋2x －1＝－2x－1；(2)原式＝a－52a－6÷(16a－3－a2－9a－3)＝a－52（a－3）÷（5＋a）（5－a）a－3＝a－52（a－3）·a－3（5＋a）（5－a）＝－110＋2a.方法总结：对于一般的分式混合运算来讲，其运算顺序与整式混合运算一样，是先乘方，再乘除，最后算加减，如果遇到括号要先算括号里面的．在此基础上，有时也应该根据具体问题的特点，灵活应变，注意方法．【类型四】先化简，再根据所给字母的值求分式的值例4.先化简，再求值：(1x－y＋1x＋y)÷2xx2＋2xy＋y2，其中x＝1，y＝－2.解析：化简时，先把括号内通分，把除法转化为乘法，把多项式因式分解，再约分，最后代值计算．解：原式＝2x（x－y）（x＋y）·（x＋y）22x＝x＋yx－y，当x＝1，y＝－2时，原式＝1＋（－2）1－（－2）＝－13.方法总结：分式的化简求值，其关键步骤是分式的化简．要熟悉混合运算的计算顺序，式子化到最简再代值计算．【类型五】先化简，再自选字母的值求分式的值例5.先化简，再选择使原式有意义而你喜欢的数代入求值：2x＋6x2－4x＋4·x－2x2＋3x－1x－2.解析：先把分式化简，再选数代入，x取除－3、0和2以外的任何数．解：原式＝2（x ＋3）（x －2）2·x －2x （x ＋3）－1x －2＝2x （x －2）－1x －2＝2－x x （x －2）＝－1x. 当x ＝1时，原式＝－1.(x 取除－3、0和2以外的任何数)方法总结：取喜爱的数代入求值时，要注意所选择的值一定满足分式分母不为0，这包括原式及化简过程中的每一步的分式都有意义．【类型六】 整体代入求值例6. 已知实数a 满足a 2＋2a －8＝0，求1a ＋1－a ＋3a 2－1·a 2－2a ＋1（a ＋1）（a ＋3）的值． 解析：首先把分式分子、分母能因式分解的先因式分解，进行约分，然后进行减法运算，最后整体代值计算．解：1a ＋1－a ＋3a 2－1·a 2－2a ＋1（a ＋1）（a ＋3）＝1a ＋1－a ＋3（a ＋1）（a －1）·（a －1）2（a ＋1）（a ＋3）＝1a ＋1－a －1（a ＋1）2＝2（a ＋1）2＝2a 2＋2a ＋1. 因为a 2＋2a －8＝0，所以a 2＋2a ＝8，2a 2＋2a ＋1＝28＋1＝29. 方法总结：利用“整体代入”思想化简求值时，先把要求值的代数式化简，然后将已知条件变换成适合所求代数式的形式，再整体代入即可．【类型七】运用分式解决实际问题例7. 有一客轮往返于重庆和武汉之间，第一次往返航行时，长江的水流速度为a 千米/小时；第二次往返航行时，正遇上长江汛期，水流速度为b 千米/小时(b ＞a )．已知该船在两次航行中，静水速度都为v 千米/小时，问该船两次往返航行所花时间是否相等，若你认为相等，请说明理由；若你认为不相等，请分别表示出两次航行所花的时间，并指出哪次时间更短些？解析：重庆和武汉之间的路程一定，可设其为s，所用时间＝顺流时间＋逆流时间，注意顺流速度＝静水速度＋水流速度；逆流速度＝静水速度－水流速度，把相关数值代入，比较即可．解：设两次航行的路程都为s.第一次所用时间为：sv＋a＋sv－a＝2vsv2－a2，第二次所用时间为：sv＋b＋sv－b＝2vsv2－b2，∵b＞a，∴b2＞a2，∴v2－b2＜v2－a2. ∴2vsv2－b2＞2vsv2－a2.∴第一次的时间要短些．方法总结：①运用分式解决实际问题时，用分式表示实际问题中的量是解决问题的关键．②比较分子相同的两个分式的大小，分母大的反而小．。

100道异分母分数加减法1. 五分之三加三分之四=八分之七2. 五分之一减三分之四=七分之十三3. 九分之三加三分之五=十二分之八4. 七分之四减五分之七=十二分之三5. 五分之三加四分之五=九分之八6. 八分之一减四分之三=四分之八7. 三分之一加九分之七=十二分之八8. 五分之四减三分之二=七分之六9. 七分之一加八分之二=十五分之三10. 六分之三减四分之五=二分之八11. 七分之五加八分之四=十五分之九12. 九分之一减三分之四=六分之五13. 五分之二加三分之六=八分之八14. 三分之五减九分之四=六分之九15. 七分之二加四分之三=十一分之五16. 六分之五减四分之一=两分之四17. 九分之三加四分之七=十三分之十18. 三分之五减八分之三=五分之八19. 五分之四加四分之五=九分之九20. 八分之一减七分之三=一分之八21. 三分之一加六分之二=九分之三22. 四分之五减九分之二=五分之七23. 三分之五加四分之七=七分之十二25. 七分之四加八分之五=十五分之九26. 六分之三减五分之四=一分之七27. 九分之四加八分之一=十七分之五28. 七分之五减八分之三=九分之八29. 九分之二加五分之四=十三分之六30. 三分之一减七分之四=十分之三31. 五分之六加四分之三=九分之九32. 八分之五减七分之二=一分之三33. 六分之一加九分之五=十五分之六34. 三分之五减八分之一=五分之四35. 九分之四加七分之三=十六分之七36. 五分之二减六分之五=一分之三37. 九分之一加五分之二=十四分之三38. 七分之三减八分之五=九分之八39. 三分之二加六分之四=九分之六40. 八分之一减五分之三=三分之八41. 三分之四加九分之一=十二分之五42. 五分之六减九分之三=四分之三43. 七分之五加六分之四=十三分之九44. 八分之一减九分之二=一分之十45. 四分之三加三分之一=七分之四46.五分之一减三分之五=二分之六47.六分之三加三分之四=九分之七48. 陆分之二减五分之四=一分之六50. 七分之五减八分之一=九分之四51. 六分之三加三分之五=九分之八52. 四分之一减七分之六=三分之七53. 五分之四加四分之四=九分之八54. 六分之五减三分之二=三分之七55. 三分之四加六分之五=九分之九56.四分之一减九分之四=五分之五57. 八分之一加六分之一=十四分之二58. 五分之六减三分之五=两分之三59. 九分之四加四分之五=十三分之九60. 七分之一减七分之五=零分之六61. 七分之三加三分之四=十分之七62. 四分之三减三分之五=一分之八63. 九分之三加六分之五=十五分之八64. 七分之一减四分之三=三分之四65. 四分之一加五分之二=九分之三66. 五分之三减八分之四=三分之七67. 九分之二加五分之四=十三分之六68. 三分之五减六分之三=三分之八69. 七分之三加八分之二=十五分之五70. 九分之一减四分之五=五分之六71. 六分之二加四分之三=十分之五72. 三分之四减七分之三=六分之七73. 六分之四加五分之三=十一分之七74. 八分之一减七分之一=一分之八75. 九分之四加八分之三=十七分之七76. 七分之五减三分之四=四分之九77. 三分之一加七分之五=十分之六78. 五分之一减四分之五=一分之十79. 九分之三加五分之一=十四分之四80. 六分之五减七分之三=三分之八81. 五分之三加八分之四=十三分之七82. 三分之二减五分之一=七分之三83. 五分之二加六分之四=十一分之六84. 七分之三减六分之五=一分之八85. 七分之一加四分之五=十一分之六86. 八分之二减三分之一=五分之七87. 九分之一加五分之三=十四分之四88. 六分之五减八分之五=两分之三89. 五分之四加七分之三=十二分之七90. 六分之一减九分之五=三分之六91. 七分之四加五分之三=十二分之七92. 四分之五减七分之一=三分之四93. 八分之三加五分之二=十三分之五94. 九分之五减三分之二=六分之三95. 七分之一加三分之五=十分之六96. 六分之三减七分之四=三分之七97. 五分之四加三分之一=八分之五98. 八分之三减四分之五=四分之八99. 六分之四加九分之五=十五分之九 100. 三分之一减五分之五=八分之六。

分式的加减法（二）——异分母分式加减教学目标：1.理解掌握异分母分式加减法法则.2.能正确熟练地进行异分母分式的加减运算.3.在课堂活动中培养学生乐于探究、合作学习的习惯；渗透类比、化归数学思想方法，提高运算能力．重点难点：重点：异分母分式的加减法法则及其运用.难点：正确确定最简公分母和灵活运用法则.教学过程一、情境引入：从甲地到乙地有两条路，每条路都是3km ，其中第一条是平路，第二条有1km 的上坡路，2km 的下坡路，小丽在上坡路上的骑车速度为vkm/h ,在平路上的骑车速度为2vkm/h ，在下坡路上的骑车速度为3vkm/h ，那么 当走第二条路时，她从甲地到乙地需要多长时间？12()3h v v+她走哪条路花费时间少？少用多长时间？123()32h v v v +-二、解读探究1、想一想，异分母分数如何加减？（学生举例） 你认为异分母的分式应该如何加减？比如314a a+应该怎样计算？ 议一议，小明认为，只要把异分母的分式化成同分母的分式，异分母分式的加减问题就变成了同分母分式的加减问题.小亮同意小明的这种看法，但他俩的具体做法不同. 小明：22231341213134444444a a a a a a a a a a a a a a a+=+=+== 小亮：3134112113444444a a a a a a a ⨯+=+=+= 你对这两种做法有何评论？与同伴交流.小结：根据分式的基本性质，异分母的分式可以化为同分母的分式，这一过程称为分式的通分.与异分母分数的加减法类似，异分母分式相加减，需要先通分，变为同分母的分式，然后再加减.为了计算方便，异分母分式通分时，通常取最简单的公分母（简称最简公分母）作为它们的共同分母.2、异分母分式的加减法法则：异分母分式相加减，先通分，变为同分母分式，然后再加减.用式子表示为：b a ±d c =bdbc ad ±. 3、分式通分时，要注意几点：（1）最简公分母的系数，取各分母系数的最小公倍数；（2）最简公分母的字母，取各分母所有字母的最高次幂的积；（3）分母的系数若是负数时，应利用符号法则，把负号提取到分式前面；（4）分母是多项式时一般需先因式分解.三、应用举例【例1】计算：（1）23+x ＋x -21＋422-x x ；（2）122-x x －x －1. 分析：（1）把分母的各多项式按x 的降幂排列，能先分解因式的将其分解因式，找最简公分母，转化为同分母的分式加减法.（2）一个整式与一个分式相加减，应把这个整式看作一个分母是1的式子来进行通分，注意－x －1=11+-x ，要注意符号问题. 解：（1）原式=23+x －21-x ＋)2)(2(2-+x x x =)2)(2()2(3-+-x x x －)2)(2(2-++x x x ＋)2)(2(2-+x x x =)2)(2(2)2()2(3-+++--x x x x x =)2)(2(2263-++---x x x x x =)2)(2(84-+-x x x =24+x ； （2）原式=122-x x 11+-x =122-x x 1)1)(1(--+-x x x =1)1)(1(22--+-x x x x =1)1(222---x x x =11222-+-x x x =112-+x x . 【例2】计算：x -11＋x +11＋212x +＋414x+. 分析：此题若将4个分式同时通分，分子将是很复杂的，计算也是比较复杂的.各式的分母适用于平方差公式，所以采取分步通分的方法进行加减.解：原式=)1)(1()1()1(x x x x -+-++＋212x +＋414x + =212x -＋212x +＋414x +=)1)(1()1(2)1(22222x x x x -+-++＋414x + =414x -＋414x +=)1)(1()1(4)1(44444x x x x -+-++=818x -. 【练习】1、计算：（1）3155a a a -+；（2）2111x x x-+-- 2、计算：（1）231x ＋x 43；（2）1624432---x x . 3、计算 2a ab a b --- 解：原式=()()b a b b a b a b a b a a b a b a a -=--+--=---2221.四、知识小结异分母分式的加减法步骤：1. 正确地找出各分式的最简公分母；2. 用公分母通分后，进行同分母分式的加减运算.3. 公分母保持积的形式，将各分子展开.4. 将得到的结果化成最简分式.五、基础知识检测1．填空题：（1）异分母分式相加减 ， 的分式，然后再加减.（2）计算：232++-x x －11+x 的结果是 . *（3）计算：13-a a －a 2－a －1= . （4）计算：)4)(2(42+-+x x x x －422-+x x = . *（5）已知x 1+y 1=m 1，则m= . 2．选择题：（1）使代数式54++x x ÷32--x x 有意义的值是 （ ） A ．x ≠－4且x ≠2 B ．x ≠5且x ≠3C ．x ≠－5且x ≠3D ．x ≠－5且x ≠3且x ≠2*（2）计算：x+1－123+-x x x 的结果是 （ ） A ．113+x B ．113-x C ．112+-x x D ．112++x x （3）若x －y=xy ≠0，那么x 1－y1等于 （ ） A ．xy 1 B ．yx -1 C ．0 D ．－1 （4）已知x 1－y 1=3，则yxy x y xy x ---+55的值是 （ ） A ．－27 B ．27 C ．0 D ．2 （5）化简ab b a 22-－22a ab b ab --得 （ ） A ．b a B ．abb a 222+ C ．a 2 D ．a －2b3．计算：（1）2312+-x x ＋6512+-x x ＋3412+-x x ； （2）x ＋11-x ＋22113x x x -+-； （3）2242y x x -＋x y -22＋1. 4．先化简，再求值：y x y -＋y x x y 2232-·222y xy x y +-，其中x=32，y=－3.六、创新能力运用计算：（1）21-x ＋12+x －12-x －21+x ； （2）41--x x －2)1(3--x x ＋2参考答案【基础知识检测】1．（1）先通分，化为同分母 ；（2）21--x ；（3）11-a ；（4）21--x x ；（5）yx xy +. 2．（1）D ；（2）C ；（3）D ；（4）B ；（5）A.3．（1）)3)(1(3--x x ；（2）13223-+-x x x x ；（3）2222444y x y y x ---. 4．xy ，－29. 【创新能力运用】（1）)1)(1)(2)(2(12-+-+x x x x ； （2）)4)(2(6--x x .七、布置作业。

§（2） 异分母分式的加减法授课时间： 年 月 日 星期 课型： 审核：【学习目标】1.经历异分母分式的加减运算和通分的过程，训练学生的分式运算能力，培养数学学习中转化未知问题为已知问题的能力.2.进一步通过实例发展学生的符号感.【学习重点】1.掌握异分母的分式加减运算.2.理解通分的意义.【学习难点】1.化异分母分式为同分母分式的过程.2.符号法则、去括号法则的应用.【学习过程】一、导学1、同分母分式加减法法则：2、尝试完成下列各题（1）24a －a 1= ； （2）a 1+b 1= ； （3）ab b a +－bc c b += ； （4）a b 3+b a 2= 。

3、异分母分式加减法法则：二、自学1、异分母分式加减法法则： 。

用字母表示是 。

2、通分时，应先确定各个分式的分母的公分母：先确定公分母的系数，取各个分母系数的 ；再取各分母所有因式的 的积。

3、通分（1）x y 2,23y x ,xy 41 （2）y x -5,2)(3x y - （3）31+x ,31-x （4）412-a ,21-a三、互学1、计算（1）31-x －31+x （2）412-a －21-a2、先化简，再求值：1222--a a a ÷（a-1－112+-a a ），其中a=213、根据规划设计，某市工程队准备在开发区修建一条长1120m 的盲道。

由于采用新的施工方式，实际每天修建盲道的长度比原计划增加10m ，从而缩短了工期。

假设原计划每天修建盲道xm ，那么（1）原计划修建这条盲道需要多少天？实际修建这条盲道需要多少天？（2）实际修建这条盲道的工期比计划缩短了几天？四、测学1、计算：（1）a b 3+ba 2 （2）11-a －212a -2、化简：（1+442-a ）.aa 2+五、思学1、通过学习你掌握了什么?请写在下面：（1）异分母分式的加减法法则： 。

用字母表示是 。

（2）确定最简公分母的方法： 。

异分母分式加减法
《异分母分式加减法，你真的懂吗？》
嘿，同学们！你们知道吗？数学的世界里有一种神奇又有点让人头疼的运算，叫做异分母分式加减法。

这玩意儿就像是一个藏着秘密的小怪兽，得把它的秘密揭开，才能战胜它！
就说上次数学考试吧，老师出了一道异分母分式加减法的题目，我一看，哎呀，这可咋整？脑袋一下子就懵了！我就像一只在迷宫里乱转的小老鼠，找不到出路。

我看看同桌，他眉头紧皱，嘴里还嘟囔着：“这什么破题啊，怎么这么难！”我心里想：“可不是嘛，这也太难了！”
这时候，我后面的学霸小李发话了：“这题不难呀，先通分不就好了嘛！”我赶紧转过头问：“怎么通分呀？”小李一脸无奈地说：“你连通分都不知道？就是找分母的最小公倍数呀！”我还是一脸迷茫，问道：“那最小公倍数又怎么找啊？”小李白了我一眼，说：“你怎么连这个都没搞懂！就比如2 和3，最小公倍数不就是6 嘛！”
我似懂非懂地点点头，开始自己琢磨。

我就想啊，这异分母分式加减法不就跟我们分糖果一样嘛。

比如说，有一堆不同大小的糖果盒子，要把里面的糖果合在一起，是不是得先把盒子变成一样大小的呀？这通分不就是把盒子变成一样大小嘛！
我按照这个思路，开始试着做题。

哎呀，好像有点眉目了！我一步一步地算着，终于算出了答案。

等老师讲题的时候，我发现自己居然做对了，心里那个高兴劲儿啊，就像大热天吃了一根冰棒，爽极了！
经过这次，我算是明白了，异分母分式加减法其实也没那么可怕。

只要我们掌握了方法，找到了窍门，就一定能把它拿下！所以呀，同学们，遇到难题别害怕，多想想，多试试，总会找到解决办法的！你们说是不是？。

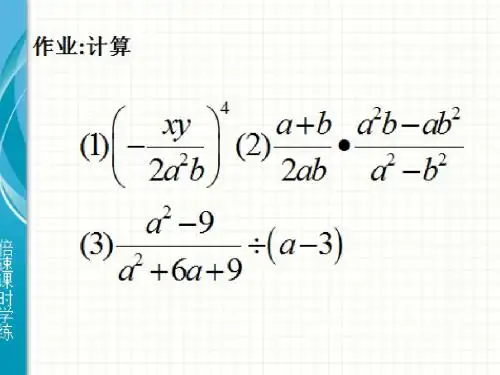
分式的加减法一、同分母的分式相加减，分母不变，分子相加减。

例1、（2012∙德阳）计算：（1）22555x x x +--=；（2）2222223223x y x y x y x y x y x y++--+---=。

变式1-1、（2012∙天津）计算：（1）21644x x x ---=；（2）2111x x x -+--=；（3）()()22111x x x ---=。

二、异分母的分子相加减，先通分，变为同分母的分式，然后相加减。

例2、a b 、为实数，且1ab =，设11,1111a b P Q a b a b =+=+++++，则P Q （填“>”“<”或“=”）。

变式2-1、已知11,,,11n n n n M N P n n n ->===-+，则M N P 、、的大小关系为。

例3、计算： （1）22142x x x ---=；（2）211a a a -++=；（3）2312224x x x x +-+--=。

变式3-1、计算：（1）222a a a --+=；（2）26342m m m --+=；（3）22b a b a b-++=；（4）222m n mn m n m n m n -+-+-=；（5）2232244m n m n m mn n ----+=；（6）22112x x y x y x y-++--=；（7）223215233249a a a a +--+--=。

三、分式的加减、乘除、乘方混合运算例4、计算：（1）（2011∙南充）221a b a b a b b a ⎛⎫-÷ ⎪-+-⎝⎭=；（2）222161816416x x x x x x ⎛⎫-+÷ ⎪++--⎝⎭=。

变式4-1、计算：（1）22221369x y x y x y x xy y+--÷--+=；（2）211111x x x x ⎛⎫÷+ ⎪--+⎝⎭=；（3）2236214422x x x x x x --⎛⎫÷- ⎪+++-⎝⎭=；（4）()222211121a a a a a a +-÷+---+=；（5）()2222222232a c a a c bc a b ⎛⎫⎛⎫-∙+÷- ⎪ ⎪⎝⎭⎝⎭=；（6）2222221121x x x x x x x ---÷+--+=；（7）22214244x x x x x x x x +--⎛⎫-÷⎪--+⎝⎭=；（8）2221111x x x ⎛⎫÷+ ⎪--+⎝⎭=。