结构力学第三章静定结构的内力计算(典型例题练习题)
- 格式:doc
- 大小:695.50 KB
- 文档页数:23



作简支梁的剪力图与弯矩图。
解:求支座反力荷载叠加法平衡方程*[例题3-2-2]作外伸梁的剪力图与弯矩图。
解:求支座反力<荷载叠加法平衡方程*作外伸梁的剪力图与弯矩图。
解:求支座反力荷载叠加法平衡方程、[例题3-3-1]作多跨静定梁的内力图。
解:求支座反力荷载叠加法&[例题3-3-2]作三跨静定梁的内力图。
解:求支座反力[[例题3-3-3]作多跨静定梁的内力图。
解:求支座反力[例题3-4-1]作静定刚架的内力图解:求支座反力)[例题3-4-2]作静定刚架的内力图解:求支座反力[例题3-4-3](作静定刚架的内力图解:求支座反力[例题3-4-4]作静定刚架的内力图解:求支座反力—[例题3-4-5]作三铰刚架的内力图解:求支座反力|[例题3-4-6]作三铰刚架的内力图解:求支座反力)[例题3-4-7]作静定刚架的内力图解:求支座反力…[例题3-4-8]作静定刚架的图解:[例题3-4-9]作静定刚架的图解:。
[例题3-4-10]作静定刚架的图解:[例题3-4-11]作静定刚架的图解:"[例题3-4-12]作静定刚架的图解:[例题3-4-13] 作静定刚架的图解:*[例题3-4-14] 作静定刚架的图解:求支座反力[例题3-4-15])作静定刚架的图解:[例题3-5-1]试绘制三铰拱的内力图。
拱轴方程为解:相应简支梁的反力和内力求支座反力.拱轴方程当时》00001050145105233315105233315533,75546403305055315-25693255-5507-45135-8581200-1150[例3-5-2]试求对称三铰拱在竖向均布荷载作用下的合理轴线。
解:相应简支梁的弯矩方程为水平推力合理轴线方程为合理轴线为一抛物线。
[例3-6-1]用结点法求桁架各杆的内力。
解:求支座反力解题路径:以结点为对象以结点为对象以结点为对象以结点为对象[例3-6-2]用结点法求桁架各杆的内力。


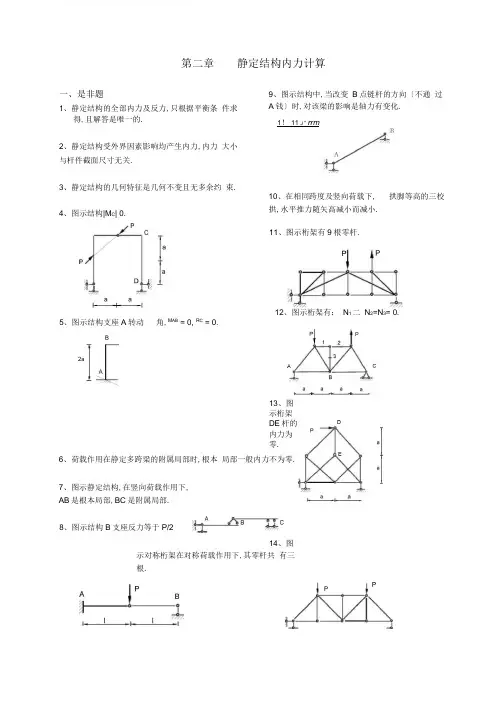
第二章静定结构内力计算一、是非题1、静定结构的全部内力及反力,只根据平衡条 件求得,且解答是唯一的. 2、静定结构受外界因素影响均产生内力,内力 大小与杆件截面尺寸无关.3、静定结构的几何特征是几何不变且无多余约 束.4、图示结构|M C | 0.9、图示结构中,当改变 B 点链杆的方向〔不通 过A 钱〕时,对该梁的影响是轴力有变化.1! 11 J “ rrm10、在相同跨度及竖向荷载下,拱脚等高的三校拱,水平推力随矢高减小而减小.12、图示桁架有: N 1 二 N 2=N 3= 0.5、图示结构支座A 转动角,M AB = 0, R C = 0.13、图示桁架DE 杆的内力为零.6、荷载作用在静定多跨梁的附属局部时,根本 局部一般内力不为零.7、图示静定结构,在竖向荷载作用下, AB 是根本局部,BC 是附属局部.14、图示对称桁架在对称荷载作用下,其零杆共 有三根.11、图示桁架有9根零杆.2a8、图示结构B 支座反力等于P/216、图示结构的零杆有 7根.18、图示桁架中,杆 1的轴力为0.二、选择题1、对图示的AB 段,采用叠加法作弯矩图是: A.可以;B.在一定条件下可以;C.不可以;D.在一定条件下不可以.3、图示结构 M K 〔设下面受拉为正〕为: A. qa 2/2 ; B. — qa 2,2 ; C. 3qa 2/2 ;D. 2qa 2 .2、图示两结构及其受载状态,它们的内力符合A.弯矩相同,剪力不同;B.弯矩相同,轴力不同;C.弯矩不同,剪力相同;D.弯矩不同,轴力不同.4、图示结构 M DC 〔设下侧受拉为正〕为:A. — Pa ;B. Pa ;C. — Pa y 2 ;D. Pa/2.19、图示为一杆段的 M 、Q 图,假设Q 图是正确的, 那么M 图一定是错误的.17、图示结构中,CD 杆的内力 Ni =— P . M图Q 图D4 a h --------------------- -l lll5、在径向均布荷载作用下,三较拱的合理轴线 为:A.圆弧线;B.抛物线;C.悬链线;D.正弦曲线.6、图示桁架C 杆的内力是:A. P ;B. — P/2 ;C. P/2 ;D. 0.三、填充题1、在图示结构中,无论跨度、高度如何变化, M CB 永远等于M BC 的.倍,使刚架_侧受拉. 2 a2 a3、对图示结构作内力分析时,应先计算 局部,再计算局部.2、[ M AB = R C = 图示结构支座 A 转动 角,7、图示桁架结构杆1的轴力为:A. 22 P ;B. - ^2 PC. J 2 P/2;D. — J 2 P/2.8、图示结构N DE 〔拉〕为:A. 70kN ;B. 80kN ;C. 75kN ;D. 64kN .10kN/m H H f H M H H5、图示梁支座B处左侧截面的剪力Q B:S =.l = 2m.20kN 20kN10kN/m;. T B... , - _______________ :1 l l l2 lI I I\-------------- 19、图示结构中,AD杆上B截面的内力M B = , 侧受拉.Q B右=,N B右=o7、图示抛物线三校拱,矢高为4m ,在D点作用力偶M =,M D 左=, M D 右=O8、图示半圆三钱拱, 为30.,V A= qa 〔f〕,H A = qa/2 〔一〕, K 截面的=, Q K = , Q K的计算式为11、三较拱在竖向荷载作用下, 其支座反力与三个钱的位置关,与拱轴形状关.12、图示结构固定支座的竖向反力V A13、图示结构1杆的轴力和K截面弯矩为:N I 5M K = 〔内侧受拉为正〕. 10、图示结构CD杆的内力为14、1m1m1m2m1m 1m 1m 1mq =10 kN/m15、图示结构中,N FE图示三较拱的水平推力N FD o四、作图题:作出以下结构的弯矩图〔组合结构要计算链杆轴力〕m o2-L3a/4 3a/4 a/2a/2----- ]——4 ----- 1—I2、40kN 40kN20kN/m4m2m 2m 2m 2m——-k——-P ---------- -4--3、12P 2 Pa4 ' /I 工a a a a ap__I 1 -------------------- 1—a-l4、m =20kN.m q=20kN/m9、a2a 2a----- +-----10、16、ii2l17、18、3m 6maa19、q22、28、29、a6 --a----------- 0-------- -- -a日上-a aI ------ 1----- 133、10kN/m'I f I H _f m2m 4—41U- 山3m 1m 1m34、10kN10kN/m4m3m35、3m 3m36、3m2m2m 41、m o42、38、qP P ■ -------- 0 --49、50、20kN m3m6kN3m 3m 2m 3m3a4m五、计算题:1、计算图示半圆三较拱 K 截面的内力 M K,N K.:q =1kN/m ,M =18kN - m .3、图示三校拱K 截面倾角 =26 33 (sin =,cos =),计算K 截面内力M K , NK . ・ 2 一 ■ y =4仅(l x)/l , (l 16m,f 4m)2、计算图示抛物线三校拱K 截面的内力 M K ,N K ,拱轴方程为:y = 4 f x(l-x)//.:P= 4kN,q=1kN/m, f=8m, | K |=45 ° .4、计算图示半圆拱 K 截面弯矩.10kN54、b2m-t -—―I F ---4m 2kwm58、2m59、5m57、60、作出以下结构的内力图Pa a a a卜———11、计算图示桁架杆1、2的内力.5、计算图示桁架中杆1、2、3的内力.6、计算图示桁架中杆1 ,2的内力.12、计算图示桁架杆1、2的内力.1.5m 1.5mI . , I ■17、计算图示桁架中杆1 ,2的内力.13、计算图示桁架结构杆1、2的轴力.8、计算图示桁架中杆1,2, 3的内力.14、计算图示桁架结构杆1、2的轴力.9、计算图示桁架杆1、2的内力.15、计算图示桁架杆1、2的轴力.17、 18、 19、 20、 计算图示桁架杆a a a的内力.ba 、a计算图示桁架杆1、2的内力.a的内力.计算图示桁架杆件4m4m计算图示桁架杆a 、b 的内力.22、计算图示桁架各杆轴力及反力.23、作图示结构的 M 图并求杆1的轴力.24、作图示结构的M 图并求链杆的轴力.d 4m .第二章 静定结构内力计算〔参考 一、是非题: 1、〔O 〕 4、〔O 〕 6、〔O 〕 9、〔O 〕 11、 〔O 〕 14、〔X 〕 16、〔O 〕 19、〔O 〕 二、选择题:1、〔A 〕〔C 〕 5、 6、〔A 〕 三、填充题: 1、 2 03、 CB4、 8kN (A) 外侧, • m 答案)2、(X)3、(O)5、(O) 7、(X) 8、(X) 10、(X) 12、(O) 13、(O) 15、(X) 17、(X)18、(O) 2、(B) 3、(C) 7、(B) 8、(B) 2、 CD (或 ACD ) 6、 4、 0 ,30kN 8、 30,(pa/2)cos(一2 Pa80M 图 6、图8、30) <qa/2)sin( 30) 9、 Pd ,下,P, 0 10、P11、12、30 kN7、13、 10壶kN , M K 20kN14、 20kN15、 4P , 0 四、作图题: 1、 2、10、1m 0 2 0A 40 an 「 | 8012-Pa+1.5 m n43mo4 0二 J-i 40120C -- a --------- B ■■■- --I 40, D -rt-M 图 kN .m133.5Pa 1519、rn;m01m0R AH BPaPa5 Pam/22 Pl1.5Pa3Pam/2PlPl-40XI253.3216.6kN .m4m. M B2二0.5ql (0.5ql2PaPa16016014161820.5 ql20.5qi211515152Pa/32Pa/3232qa15qi2D 2Pa一22、F 15「5D ,图(kN.m)2Pa/32Pa/32qa2qa151524、Pa -Paqa2 2 2Pa3Pa 2qa PaPa20、pa1.5papa j 1.5 paPapa 0.5 pa3P /2ql2/2,2ql/25 P/2 13P/2PaPaqi 2/228、3029、1010Pa PaPaPa2Pa2PaPa0.533、34、0.5 18100.1251230101010ql2) 小211178136243630、35、N= —28.8kNN=4.5qa4 ----------- 1N=_gqa36、—4.5qa24.5qa"41一54543636M图2qa 22qa 239、40、A-Pa45、46、2Pa M 图qaPl47、 41、 42、>O g mA1 2 D n1- —Pa 3E48、43、,F2 -Pa44、56 72X A = 30 kN-XY A = 2kNX B =18 kNY B =6 kN五、计算题:1、H = 3Kn, M K = kN m , N K =2、H = 3kN , M K = 2kN • m , N K = kN3、M K 15kN m (下 拉),N k4.470kN4〞 一3Pl丁 |__Pl 7 M-1Pl d -4 N1图Pl-251、52、53、 60kN 57、 2111----58、1632254、59、Pl60、「J55、56、M 图 kN .mN 12-. 2P/3 N 2Pl34Pl 37.5N 图(kN)Q 图(kN)51521512.52 2P /34 、 V 0.5P 〔 〕, H 0.289P 〔〕R M K V A 〔R ——〕 2 5、N = 0 , N = 4P H A -R 0.058PR 〔X 〕 2 〔拉〕,N 3 J 5P 〔压〕 6、N i = 3 = 〔拉〕,N 2=— 2P/3 =-〔压〕 7、 N i =+>/2 〔压〕,N 2 =干〔压〕 8、N i = 120kN 〔拉〕,N 2 = 0, N 3= 198kN 〔拉〕 9、N i 0, N 2 <12P 10、N i 0, M P, N 3 72P/2 ii 、N 2 P , N i 0.6P '' i2、对称情况:N i N 2 0 ,N i N ; N ;..2P反对称情况: N i N 2u 2 P ,N 2 N 2 N 2 ,2P i3、N i 2P,N 2 2.236P i4、 N i 05P , N 2 P i5、N i = v'5 P/2, N 2 = P i6、 N a 20kN 3、5 一 i7、N a -P, N b 0 4 i8、N= 0, N= 43P i9、N a =- 2P/3 20、N i P ,N 2 1414P 2i 、 N a = i00 kN , N b =0 M 图22、 23、i2 N i。


1、杆系结构中梁、刚架、桁架及拱的分类,是根据结构计算简图来划分的。
(正确)2、定向支座总是存在—个约束反力矩(正确)和一个竖向约束反力。
(错误)3静力和动力荷载的区别,主要是取决于它随时间变化规律、加载速度的快慢。
其定性指标由结构的自振周期来确定。
(正确)4、铰结点的特性是被连杆件在连接处既不能相对移动,(正确)又不能相对转动。
(错误)5、线弹性结构是指其平衡方程是线性的,(正确)变形微小,(正确)且应力与应变之间服从虎克定律。
(正确)1、学习本课程的主要任务是:研究结构在各种外因作用下结构内力与()计算,荷载作用下的结构反应;研究结构的()规则和()形式等问题。
正确答案:位移,动,组成,合理2、支座计算简图可分为刚性支座与弹性支座,其中刚性支座又可分为()、()、()和()。
正确答案:链杆,固定铰支座,固定支座,滑动支座3、永远作用在结构上的荷载称为固定荷载,暂时作用在结构上的荷载称为()它包括()、()、()、()和()等正确答案:活载,风,雪,人群,车辆,吊车4、刚节点的特性是被连接的杆件载连接处既无()又不能相对();既可传递(),也可传递()正确答案:移动,转动,力,力矩第二章平面体系的几何构成分析1、图中链杆1和2的交点O可视为虚铰。
()O正确答案:正确2、两刚片或三刚片组成几何不变体系的规则中,不仅指明了必需的约束数目,而且指明了这些约束必须满足的条件。
()正确答案:正确3、在图示体系中,去掉1-5,3-5,4-5,2-5,四根链杆后,的简支梁12,故该体系具有四个多余约束的几何不变体系。
()12345正确答案:错误4、几何瞬变体系产生的运动非常微小并很快就转变成几何不变体系,因而可以用作工程结构。
()正确答案:错误5、图示体系是几何不变体系。
()正确答案:错误2-2几何组成分析1.正确答案:几何不变,且无多余联系。
2.(图中未编号的点为交叉点。
)A B CDEF正确答案:铰接三角形BCD视为刚片I,AE视为刚片II,基础视为刚片III;I、II间用链杆AB、EC构成的虚铰(在C点)相连,I、III间用链杆FB和D处支杆构成的虚铰(在B点)相联,II、III 间由链杆AF和E处支杆构成的虚铰相联3.(图中未画圈的点为交叉点。

结构力学习题第2章平面体系的几何组成分析2-1~2-6 试确定图示体系的计算自由度。
题2-1图题2-2图题2-3图题2-4图题2-5图题2-6图2-7~2-15 试对图示体系进行几何组成分析。
若是具有多余约束的几何不变体系,则需指明多余约束的数目。
题2-7图题2-8图题2-9图题2-10图题2-11图题2-12图题2-13图题2-14图题2-15图题2-16图题2-17图题2-18图题2-19图题2-20图题2-21图2-1 1W=2-1 9W-=2-3 3-W=2-4 2W-=2-5 1W=-2-6 4=W-2-7、2-8、2-12、2-16、2-17无多余约束的几何不变体系2-9、2-10、2-15具有一个多余约束的几何不变体系2-11具有六个多余约束的几何不变体系2-13、2-14几何可变体系为2-18、2-19 瞬变体系2-20、2-21具有三个多余约束的几何不变体系第3章静定梁和静定平面刚架的内力分析3-1 试作图示静定梁的内力图。
(a)(b)(c) (d)习题3-1图3-2 试作图示多跨静定梁的内力图。
(a)(b)(c)习题3-2图3-3~3-9 试作图示静定刚架的内力图。
习题3-3图习题3-4图习题3-5图习题3-6图习题3-7图习题3-8图习题3-9图3-10 试判断图示静定结构的弯矩图是否正确。
(a)(b)(c)(d)部分习题答案3-1 (a )m kN M B ⋅=80(上侧受拉),kN F RQB 60=,kN F L QB 60-=(b )m kN M A ⋅=20(上侧受拉),m kN M B ⋅=40(上侧受拉),kN F RQA 5.32=,kN F L QA 20-=,kN F LQB 5.47-=,kN F R QB 20=(c) 4Fl M C =(下侧受拉),θcos 2F F L QC =3-2 (a) 0=E M ,m kN M F ⋅-=40(上侧受拉),m kN M B ⋅-=120(上侧受拉)(b )m kN M RH ⋅-=15(上侧受拉),m kN M E ⋅=25.11(下侧受拉)(c )m kN M G ⋅=29(下侧受拉),m kN M D ⋅-=5.8(上侧受拉),m kN M H ⋅=15(下侧受拉) 3-3 m kN M CB ⋅=10(左侧受拉),m kN M DF ⋅=8(上侧受拉),m kN M DE ⋅=20(右侧受拉) 3-4 m kN M BA ⋅=120(左侧受拉)3-5 m kN M F ⋅=40(左侧受拉),m kN M DC ⋅=160(上侧受拉),m kN M EB ⋅=80(右侧受拉)3-6 m kN M BA ⋅=60(右侧受拉),m kN M BD ⋅=45(上侧受拉),kN F QBD 46.28=3-7 m kN M C ⋅=70下(左侧受拉),m kN M DE ⋅=150(上侧受拉),m kN M EB ⋅=70(右侧受拉) 3-8 m kN M CB ⋅=36.0(上侧受拉),m kN M BA ⋅=36.0(右侧受拉) 3-9 m kN M AB ⋅=10(左侧受拉),m kN M BC ⋅=10(上侧受拉) 3-10 (a )错误 (b )错误 (c )错误 (d )正确第4章 静定平面桁架和组合结构的内力分析4-1 试判别习题4-1图所示桁架中的零杆。
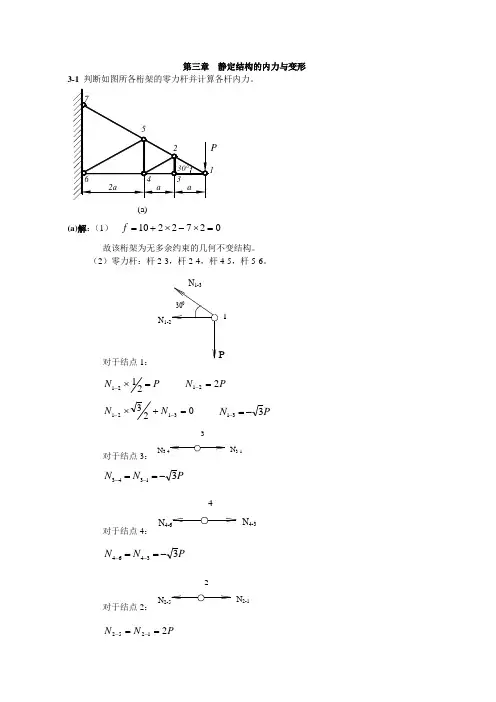
第三章 静定结构的内力与变形3-1 判断如图所各桁架的零力杆并计算各杆内力。
1P(a) (a)解:(1)0272210=⨯-⨯+=f故该桁架为无多余约束的几何不变结构。
(2)零力杆:杆2-3,杆2-4,杆4-5,杆5-6。
对于结点1:N 1-2PN 1-33001P N =⨯-2121 P N 221=-0233121=+⨯--N N P N 331-=-对于结点3:N 3-43N 3-1P N N 31343-==--对于结点4:N 4-64N 4-3P N N 33464-==--对于结点2:N 2-52N 2-1PN N 21252==--对于结点5:N 5-75N 5-2P N N 22575==--(b)(b)解:(1)082313=⨯-+=f故该桁架为无多余约束的几何不变结构。
(2)零力杆:杆1-2,杆2-3,杆2-4,杆5-4,杆6-4,杆6-7,杆6-8,杆1-5。
对于结点5:P5N 5-8P N -=-85对于结点8:N 7-88N 5-8Fθ05528785=+⨯--N N P N 55287=-对于结点7:N 7-47N 7-8P N 55247=-对于结点4:N 3-44N 7-4P N N 5524743==--对于结点3:N 1-33N 3-4P N N 5524331==--2(c)(c)解:(1)026228=⨯-⨯+=f故该桁架为无多余约束的几何不变结构。
(2)零力杆:杆1-2,杆2-3,杆2-4,杆4-3,杆4-6。
对于结点1:N 1-61N 1-3Pθ05561=+⨯-P N P N 561-=-05526131=⨯+--N N P N 231=-对于结点3:3N 3-1N 3-5P N N 21353==--(e)(d)解:(1)02112316=⨯-⨯+=f故该结构为无多余约束的几何不变结构。
(2)零力杆:杆4-5,杆5-6,杆4-6,杆7-6,杆2-3,杆2-8,杆2-9,杆1-2,杆9-11,杆8-9,杆9-11.对于结点4:4N 4-7N 3-4450PP N 2243=- P N 2274=-对于结点7:7N 4-7N 3-7N 8-7P N N 22227374=⨯-=-- P N -=-73P N 2278=-对于结点3:3N 3-4N 3-7N 8-7022734332=⨯+=---N N N P N 2283=-对于结点8:022228982=⨯⎪⎭⎫ ⎝⎛+=--N P N运用截面法:N 1-2N 9-10N 9-11PP23456789由对9点的力矩平衡:0222221=⨯⨯-⨯+⨯-P a P a a N 021=-N对于结点9:9N 2-9N 9-11N 9-10N 9-88911910922---=⨯+N N N P N 22109-=-8N 3-8(e)(e)解:(1)024125=⨯-++=f故该结构为无多余约束的几何不变结构。
第三章平面静定结构受力分析静定结构受力分析之歌内力分析要提升,等效截面法冲锋。
内力标记有新规,杆段截面都分明。
剪力轴力与前无异,弯矩顺时针恒正。
受力图上力已知,叠加绘图分分钟。
一、基本概念和公式1.任意截面x 的内力分量的求法。
图3-1截面x 上的内力分量表示段x 截面(a)(b)2q(c)32qa /2qa /-2e M qa =Cx F qa=Ax F qa=-AB C对于如题图3-1所示的平面力系,平衡截面法可表为N,,,Q,,,()()xA i x i xAxxCxA i y i yAxxCxA C i C i AxxCF F F F F F M M F M F =-==-==-=∑∑∑∑∑∑(3-1)N,,,Q,,,()()xC i x i xxCxAxC i y i yxCxAxC C i C i xCxAF F F F F F M M F M F =-==-==-=∑∑∑∑∑∑(3-2)式(3-1)中的第一个等式表明:Ax 段x 截面的内力分量等于本段上外力在相应方向上投影(或力矩)的代数和的负值—平衡截面法,第二个等式表明:Ax 段x 截面的内力分量等于另段xC 上的外力在相应方向上投影(或力矩)的代数和—等效截面法。
式(3-2)第一个等式表明:xC 段x 截面的内力分量等于本段上外力在相应方向上投影(或关于截面形心C 的力矩)的代数和的负值—平衡截面法,第二个等式表明:xC 段x 截面的内力分量等于另段Ax 上的外力在相应方向上投影(或力矩)的代数和—等效截面法。
式(3-1)的第二个等式更深刻和具体的表述为:Ax 段x 截面的内力的主矢和主矩等于xC 段上所有外力关于x 截面形心的主矢和主矩。
用内力分量表示就是:(1)Ax 段x 截面的轴力N,xA F 等于xC 段上所有外力在轴线方向投影的代数和;(2)剪力Q,xA F 等于xC 段上所有外力在竖直方向投影的代数和;(3)弯矩xA M 等于xC 段上所有外力关于x 截面形心的力矩的代数和。
第3章 静定结构的内力分析习题解答习题 是非判断题(1) 在使用内力图特征绘制某受弯杆段的弯矩图时,必须先求出该杆段两端的端弯矩。
( )(2) 区段叠加法仅适用于弯矩图的绘制,不适用于剪力图的绘制。
( ) (3) 多跨静定梁在附属部分受竖向荷载作用时,必会引起基本部分的内力。
( ) (4) 习题(4)图所示多跨静定梁中,CDE 和EF 部分均为附属部分。
( )习题(4)图(5) 三铰拱的水平推力不仅与三个铰的位置有关,还与拱轴线的形状有关。
( ) (6) 所谓合理拱轴线,是指在任意荷载作用下都能使拱处于无弯矩状态的轴线。
( ) (7) 改变荷载值的大小,三铰拱的合理拱轴线形状也将发生改变。
( ) (8) 利用结点法求解桁架结构时,可从任意结点开始。
( )【解】(1)正确;(2)错误; (3)正确;(4)正确;EF 为第二层次附属部分,CDE 为第一层次附属部分;(5)错误。
从公式0H /C F M f 可知,三铰拱的水平推力与拱轴线的形状无关;(6)错误。
荷载发生改变时,合理拱轴线将发生变化; (7)错误。
合理拱轴线与荷载大小无关;(8)错误。
一般从仅包含两个未知轴力的结点开始。
习题 填空(1)习题(1)图所示受荷的多跨静定梁,其定向联系C 所传递的弯矩M C 的大小为______;截面B 的弯矩大小为______,____侧受拉。
P习题(1)图(2) 习题(2)图所示风载作用下的悬臂刚架,其梁端弯矩M AB =______kN ·m ,____侧受拉;左柱B 截面弯矩M B =______kN ·m ,____侧受拉。
习题(2)图(3) 习题(3)图所示三铰拱的水平推力F H 等于 。
习题(3)图(4) 习题(4)图所示桁架中有 根零杆。
习题(4)图【解】(1)M C = 0;M C = F P l ,上侧受拉。
CDE 部分在该荷载作用下自平衡;(2)M AB =288kN ·m ,左侧受拉;M B =32kN ·m ,右侧受拉; (3)F P /2;(4)11(仅竖向杆件中有轴力,其余均为零杆)。
第三章 静定结构的位移计算一、判断题:1、虚位移原理等价于变形谐调条件,可用于求体系的位移。
2、按虚力原理所建立的虚功方程等价于几何方程。
3、在非荷载因素(支座移动、温度变化、材料收缩等)作用下,静定结构不产生内力,但会有位移且位移只与杆件相对刚度有关。
4、求图示梁铰C 左侧截面的转角时,其虚拟状态应取:A.;; B.D.C.=1=15、功的互等、位移互等、反力互等和位移反力互等的四个定理仅适用于线性变形体系。
6、已知M p 、M k 图,用图乘法求位移的结果为:()/()ωω1122y y EI +。
M k M p 21y 1y 2**ωω( a )M =17、图a 、b 两种状态中,粱的转角ϕ与竖向位移δ间的关系为:δ=ϕ 。
8、图示桁架各杆E A 相同,结点A 和结点B 的竖向位移均为零。
a a9、图示桁架各杆EA =常数,由于荷载P 是反对称性质的,故结点B 的竖向位移等于零。
二、计算题:10、求图示结构铰A 两侧截面的相对转角ϕA ,EI = 常数。
q l l l /211、求图示静定梁D 端的竖向位移 ∆DV 。
EI = 常数 ,a = 2m 。
a a a 10kN/m12、求图示结构E 点的竖向位移。
EI = 常数 。
l l l /3 2 /3/3q13、图示结构,EI=常数 ,M =⋅90kN m , P = 30kN 。
求D 点的竖向位移。
P 3m 3m 3m14、求图示刚架B 端的竖向位移。
ql15、求图示刚架结点C 的转角和水平位移,EI = 常数 。
q16、求图示刚架中D点的竖向位移。
EI =常数。
l/217、求图示刚架横梁中D点的竖向位移。
EI=常数。
18、求图示刚架中D点的竖向位移。
E I = 常数。
qll l/219、求图示结构A、B两截面的相对转角,EI=常数。
l/23l/320、求图示结构A、B两点的相对水平位移,E I = 常数。
ll21、求图示结构B点的竖向位移,EI = 常数。
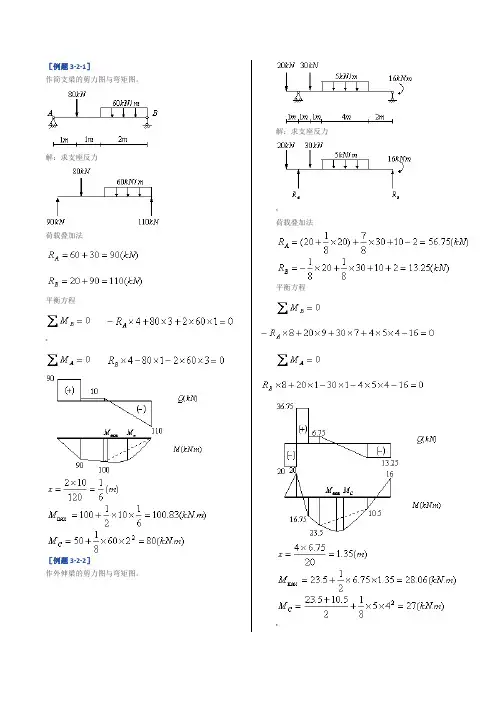
[例题3-2-1]
作简支梁的剪力图与弯矩图。
解:求支座反力
荷载叠加法
平衡方程
[例题3-2-2]
作外伸梁的剪力图与弯矩图。
解:求支座反力荷载叠加法
平衡方程
[例题3-2-3]
作外伸梁的剪力图与弯矩图。
解:求支座反力
荷载叠加法
平衡方程
[例题3-3-1]
作多跨静定梁的内力图。
解:求支座反力荷载叠加法
[例题3-3-2]
作三跨静定梁的内力图。
解:求支座反力
[例题3-3-3]
作多跨静定梁的内力图。
解:求支座反力[例题3-4-1]
作静定刚架的内力图解:求支座反力
[例题3-4-2]
作静定刚架的内力图
解:求支座反力
[例题3-4-3]
作静定刚架的内力图解:求支座反力
[例题3-4-4]
作静定刚架的内力图解:求支座反力
[例题3-4-5]
作三铰刚架的内力图解:求支座反力
[例题3-4-6]
作三铰刚架的内力图解:求支座反力
[例题3-4-7]
作静定刚架的内力图解:求支座反力
[例题3-4-8]
作静定刚架的图解:
[例题3-4-9]
作静定刚架的图解:
[例题3-4-10]
作静定刚架的图解:
[例题3-4-11]
作静定刚架的图
解:
[例题3-4-12]
作静定刚架的图
解:
[例题3-4-13] 作静定刚架的
图
解:
[例题3-4-14] 作静定刚架的
图
解:求支座反力
[例题3-4-15] 作静定刚架的
图
解:
[例题3-5-1]
试绘制三铰拱的内力图。
拱轴方程为
解:相应简支梁的反力和内力
求支座反力
拱轴方程
当时
00001050
145105
233315105
2333155
33,755
4640330505
5315-25
693255-550
7-45135-85
81200-1150
[例3-5-2]
试求对称三铰拱在竖向均布荷载作用下的合
理轴线。
解:相应简支梁的弯矩方程为
水平推力
合理轴线方程为
合理轴线为一抛物线。
[例3-6-1]
用结点法求桁架各杆的内力。
解:求支座反力
解题路径:
以结点为对象
以结点
为对象
以结点
为对象
以结点
为对象
[例3-6-2]
用结点法求桁架各杆的内力。
解:求支座反力
平衡方程
荷载叠加法
解题路径:
以结点为对象
以结点
为对象
以结点为对象
以结点
为对象
以结点
为对象
以结点
为对象
以结点
为对象
[例3-6-3]
用结点法求桁架各杆的内力。
解:利用对称性,求支座反力
解题路径:
以结点为对象
以结点为对象
以结点为对象
以结点为对象
例3-6-4]
指出桁架的零杆。
解:
[例3-6-5]
指出桁架的零杆。
解:[例3-6-6]
指出桁架的零杆。
解:
[例3-6-7]
指出桁架的零杆。
解:
[例3-6-8]
求桁架中杆件、、的内力。
解:求支座反力
截取
,取左半部分为隔离体
其中
(压力)
其中
(拉力)
截取
,取左半部分为隔离体
(压力)
[例3-6-9] 求桁架中杆件
的内力。
解:求支座反力
截取
,取左半部分为隔离体
(压力)[例3-6-10]
求桁架中杆件的内力。
解:求支座反力
截取,取右半部分为隔离体
[例3-6-11]
求桁架中杆件、的内力。
解:判断零杆
求支座反力
截取,取左半部分为隔离体
方法2:取结点为对象
[例3-6-12]
求桁架中杆件的内力。
解:
方法1:截取,取内部为隔离体
其中
方法2:取结点为对象
其中
[例3-6-13]
求桁架中杆件、的内力。
解:
截取,取内部为隔离体
[例3-6-14]
求桁架中杆件、的内力。
解:
截取,取左半部分为隔离体
[例3-6-15]
求桁架中杆件、的内力。
解:求支座反力
截取,取左半部分为隔离体
截取,取左半部分为隔离体
[例3-6-16]
求桁架中杆件、的内力。
解:求支座反力
截取,取左半部分为隔离体
截取,取上半部分为隔离体
[例3-7-1]
作五角形组合屋架的内力图。
解:求支座反力,利用对称性
求链杆的内力,截取,取左半部分为对象
取结点为对象
求梁式杆的内力,控制点的弯矩
[例3-7-2]
作三角形组合屋架的内力图。
解:求支座反力,利用对称性
截取,取左半部分为对象
作内力图
[例3-7-3]
作组合结构的内力图。
解:求支座反力
取整体为对象
取左半部为对象
取整体为对象
截取,取左半部分为对象
截取,取右半部分为对象
取结点为对象
取结点为对象
取结点为对象
取结点为对象。