结构力学静定结构内力计算

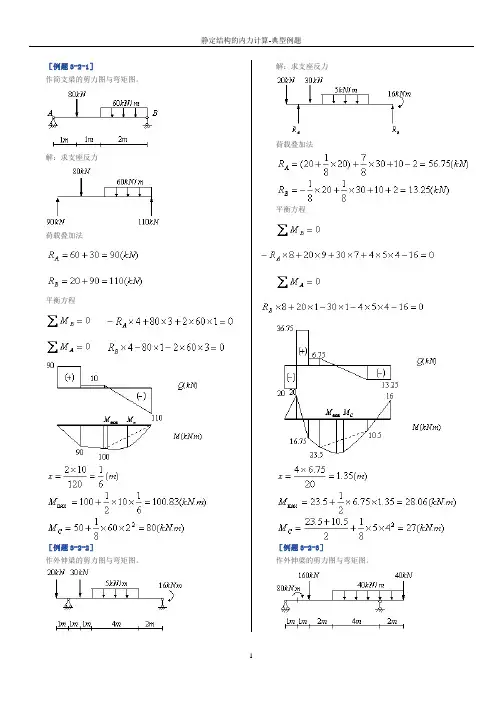
［例题3-2-1］作简支梁的剪力图与弯矩图。

解：求支座反力荷载叠加法平衡方程［例题3-2-2］作外伸梁的剪力图与弯矩图。

解：求支座反力荷载叠加法平衡方程［例题3-2-3］作外伸梁的剪力图与弯矩图。

解：求支座反力荷载叠加法平衡方程［例题3-3-1］作多跨静定梁的内力图。

解：求支座反力荷载叠加法［例题3-3-2］作三跨静定梁的内力图。

解：求支座反力［例题3-3-3］ 作多跨静定梁的内力图。

解：求支座反力［例题3-4-1］ 作静定刚架的内力图解：求支座反力［例题3-4-2］作静定刚架的内力图解：求支座反力［例题3-4-3］作静定刚架的内力图解：求支座反力［例题3-4-4］作静定刚架的内力图解：求支座反力［例题3-4-5］作三铰刚架的内力图解：求支座反力［例题3-4-6］作三铰刚架的内力图解：求支座反力??［例题3-4-7］作静定刚架的内力图解：求支座反力［例题3-4-8］作静定刚架的图解：［例题3-4-9］作静定刚架的图解：［例题3-4-10］作静定刚架的图解：［例题3-4-11］作静定刚架的图解：［例题3-4-12］作静定刚架的图解：［例题3-4-13］作静定刚架的图解：［例题3-4-14］作静定刚架的图解：求支座反力?［例题3-4-15］作静定刚架的图解：［例题3-5-1］???求支座反力当时?????? ? ?????［例3-5-2］??? 试求对称三铰拱在竖向均布荷载作用下的合理轴线。

解：相应简支梁的弯矩方程为水平推力合理轴线方程为合理轴线为一抛物线。

［例3-6-1］用结点法求桁架各杆的内力。

解：求支座反力解题路径：以结点为对象以结点为对象以结点为对象以结点为对象［例3-6-2］用结点法求桁架各杆的内力。

解：求支座反力平衡方程荷载叠加法解题路径：以结点为对象以结点为对象以结点为对象以结点为对象以结点为对象以结点为对象以结点为对象［例3-6-3］用结点法求桁架各杆的内力。

解：利用对称性，求支座反力解题路径：以结点为对象?以结点为对象以结点为对象以结点为对象例3-6-4］指出桁架的零杆。

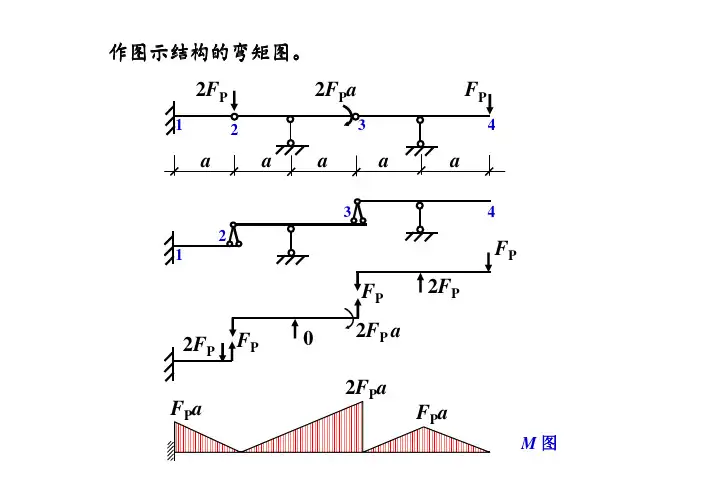
M 图分析分析：EB 杆件无弯矩杆件无弯矩→→杆件无弯矩杆件无弯矩→0kN 2445cos =−oB F 0=AMkN(4↓=I F求图示桁架指定杆件内力。

求图示桁架指定杆件内力。

(分析方法)1 1 F F FF F 1 1例 计算图示组合结构。

计算图示组合结构。

FP A D a 2FP /3 F a Ⅰ a/2 a/2 Ⅰ E G a B解A D 2FP /3 FP /3 F FP CFNCD FSCD FNFGC∑M ∑F ∑FC= 0 FNFG = FP / 2FNFAFNDFFy= 0 FSCD = FP / 3 = 0 FNCD = − FP / 2FP /2x∑Fx= 0 FNFA = 2 FP / 2= 0 FNDF = − FP / 2一般情况下应先计算链杆的轴力 取隔离体时不要截断 取隔离体时不要截断受弯杆件 不要截断受弯杆件∑Fy例：作组合结构的内力图 解 FP E D a A a C B aFP有无零杆?FNECFNDC FNDBFN DB = FPFN EC = −2 FPFN DC = 0FP a 2FP aFP 2FP -2FP FPM图FS图FN图例：计算图示组合结构。

计算图示组合结构。

FP E G FP A 0 a a a 2FPB取隔离体FJBC FNEFF J B C a 2FP 2FP -2FP FP a 2FP 2FP CF J aFNGJa B解：1、求支反力 2、求FNEF、FNGJ∑M = 0 F = 2F (↑) ∑F = 0 F = 2F (↓)Cy PyByP∑M ∑FJ=0FN EF = −2 FP2FP ax=0FN GJ = 2 FP内力图例：计算图示组合结构。

计算图示组合结构。

4m 5kN/m 15kN B C D E解：左边为基本部分， 左边为基本部分， 右边为附属部分。

右边为附属部分。

10kN 20 40A 2m 5 15 10 4mF 4mG 10 30 52m 2m20 （2.5）10 5 1012.52.55M图(kN·m)例：分析图示组合结构。

第二章 静定结构内力计算一、判断题：1、静定结构的全部内力及反力，只根据平衡条件求得，且解答是唯一的。

2、静定结构受外界因素影响均产生内力，内力大小与杆件截面尺寸无关。

3、静定结构的几何特征是几何不变且无多余约束。

4、图(a)所示结构||M C =0。

(a)BCa aAϕ2a2(b)5、图(b)所示结构支座A 转动ϕ角，M AB = 0， R C = 0。

6、荷载作用在静定多跨梁的附属部分时，基本部分一般内力不为零。

7、图(c)所示静定结构，在竖向荷载作用下，AB 是基本部分，BC 是附属部分。

ABC(c)8、图(d)所示结构B 支座反力等于P /2()↑。

(d)9、图(e)所示结构中，当改变B 点链杆的方向（不通过A 铰）时，对该梁的影响是轴力有变化。

ＡＢ(e)10、在相同跨度及竖向荷载下，拱脚等高的三铰拱，水平推力随矢高减小而减小。

11、图(f)所示桁架有9根零杆。

(f)a a a a(g)12、图(g)所示桁架有：N 1=N 2=N 3= 0。

13、图(h)所示桁架DE 杆的内力为零。

a a(h)(i)14、图(i)所示对称桁架在对称荷载作用下，其零杆共有三根。

15、图(j)所示桁架共有三根零杆。

(j)(k)16、图(k)所示结构的零杆有7根。

17、图(l)所示结构中，CD 杆的内力N 1 = P 。

(l)4a(m)18、图(m)所示桁架中，杆1的轴力为0。

二、作图题：作出下列结构的弯矩图（组合结构要计算链杆轴力）。

19、 20、2m2m2m2m4m 21、22、23、24、10kN/m.25、26、qa 27、28、a29、30、31、32、aaam33、 34、ll35、36、6m37、 38、llqq39、 40、a 2a41、42、3m43、44、45、46、2ql3m3m 47、48、49、50、.51、52、53、54、2aABCDEF4m2m55、56、2m2mqa57、 58、4m59、60、l61、62、l/2qlqP63、 64、ql65、 66、aa a a267、68、ll llaa a a69、70、.a71、72、73、74、2kN/m75、76、77、78、a三、计算题：79、计算图示半圆三铰拱K截面的内力M K，N K。

第三章 静定结构的内力计算内容提要1、静定梁（1） 内力。

静定梁在任意荷载作用下，其截面上一般有三个内力分量，即轴力N F 、剪力s F 和弯矩M 。

内力符号规定如下：轴力以拉力为正，剪力以绕隔离体内部任一点顺时针转动为正，弯矩以使梁的下边纤维受拉力正。

（2） 内力图。

内力图是反映结构中各个截面上内力变化规律的图形。

其绘制方法可归纳如下：1）基本法。

先用理论力学的基本方法求外力；再用结构力学理论列内力方程；最后用数学方法绘图2）微分关系法。

在直梁中荷载集度q 、剪力s F 弯矩M 之间有如下关系（荷载集度向上为正）：)()(x q dxx dF s = )()(x F dxx dM s = )()(22x q dx x M d = 以外力不连续点为分段点，如集中力及力偶作用点、分布荷载的两个端点等。

用截面法求得各分段点截面上的内力值，再由上述微分关系式可描绘出内力图的形状。

3）区段叠加法。

当梁段上作用有几个荷载时，则可用叠加原理绘制梁段的内力图。

先求出杆段始端、末端的弯矩竖标，连一虚直线，然后以该连线为基线，叠加相应简支梁在区段荷载作用下的弯矩图。

（3）多跨静定梁是主从结构，由附属部分和基本部分组成。

其受力特点是：外力作用在基本部分时，附属部分不受力；外力作用在附属部分时，附属部分和基本部分都受力。

其计算方法是：先算附属部分，将附属部分上的反方向加在基本部分上，再算基本部分。

所以多跨静定梁可以拆成若干个单跨梁分别进行内力计算，然后将各单跨梁的内力图连在一起即可得多跨静定梁的内力图。

上述多跨静定梁的计算方法，同样适用于其他型式的主从结构。

2．静定刚架静定刚架的内力计算方法，原则上与静定梁相同。

通常先由理论力学的基本方法求出支座反力，然后按静定梁计算内力的方法杆绘制内力图。

在绘制刚架的弯矩图时，不定义弯矩的正负号，只将弯矩图绘在杆件的受拉侧，剪力、轴力的正负号规定与静定梁相同。

3．三铰拱（1）水平推力。