第三章3.2静定结构支座反力的计算

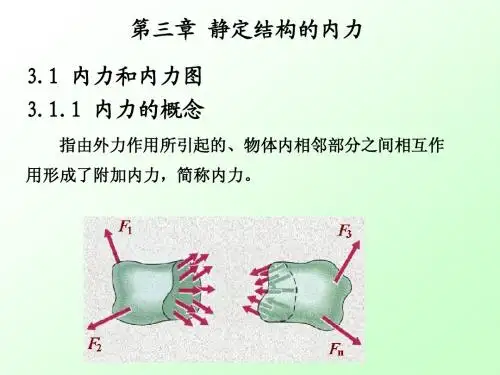
第三章静定结构的受力计算1. 教学内容从几何构造分析的角度看，结构必须是几何不变体系。

根据多余约束n ，几何不变体系又分为：有多余约束( n > 0)的几何不变体系——超静定结构；无多余约束( n = 0)的几何不变体系——静定结构。

从求解内力和反力的方法也可以认为：静定结构：凡只需要利用静力平衡条件就能计算出结构的全部支座反力和杆件内力的结构。

超静定结构：若结构的全部支座反力和杆件内力，不能只有静力平衡条件来确定的结构。

2. 教学目的进一步巩固杆件受力分析和内力分析的特点；理解多跨静定梁、静定平面刚架、静定桁架的概念；熟练掌握多跨静定梁、静定平面刚架、静定桁架内力的计算方法，能够画出内力图；理解截面法、结点法、联合法，熟练求出静定桁架的内力。

3. 主要章节第一节、单跨静定梁第二节、多跨静定梁第三节静定平面刚第四节、三铰拱架第五节、静定平面桁架第六节、组合结构4. 学习指导本章所学内容的基础是以前所学的“隔离体和平衡方程”，但是不能认为已经学过了，就有所放松。

其实，在静定结构的静力分析中，虽然基本原理不多，平衡方程只有几种形式，但是其变化是无穷的，因此重要的是知识的应用能力。

为了能够熟中生巧，在学习时应多做练习。

5. 参考资料《建筑力学教程》P21～P57第一节、单跨静定梁一. 教学目的复习材料力学中的内力概念和计算方法，梁的内力图的画法；熟练掌握各种荷载作用下的梁的内力图画法；掌握叠加法画弯矩图。

二. 主要内容1. 内力的概念和表示2. 内力的计算方法3. 内力图与荷载的关系4. 分段叠加法三. 参考资料《建筑力学》P21～P26各种《材料力学》教材3.1.1 内力的概念和表示在平面杆件的任意截面上，将内力一般分为三个分量：轴力F N、剪力F Q 和弯矩M(图3-1)。

轴力----截面上应力沿轴线方向的合力,轴力以拉力为正。

剪力----截面上应力沿杆轴法线方向的合力,剪力以截开部分顺时针转向为正。

1 结构力学多媒体课件◆几何特性：无多余约束的几何不变体系◆静力特征：仅由静力平衡条件可求全部反力和内力◆常见静定结构：梁、刚架、三铰拱、桁架和组合结构。

◆静定结构受力分析的内容：反力和内力的计算，内力图的绘制和受力性能分析。

◆静定结构受力分析的基本方法：选取脱离体，建立平衡方程。

◆注意静力分析（拆）与构造分析（搭）的联系◆学习中应注意的问题：多思考,勤动手。

本章是后面学习的基础，十分重要,要熟练掌握！容易产生的错误认识：“静定结构内力分析无非就是选取隔离体，建立平衡方程，以前早就学过了，没有新东西”一、反力的计算4kN1kN/mDCBA2m2m 4mCB A20kN/m 4m4m2m6mDCB A（1）上部结构与基础的联系为3个时，对整体利用3个平衡方程，就可求得反力。

（2）上部结构与基础的联系多于三个时，不仅要对 整体建立平衡方程，而且必须把结构打开， 取隔离体补充方程。

1、内力分量及正负规定轴力F N ：截面上应力沿杆轴法线方向的合力。

以拉力为正，压力为负。

剪力F Q ：截面上应力沿杆轴切线方向的合力。

以绕隔离体顺时针转为正,反之为负。

弯矩M ：截面应力对截面中性轴的力矩。

不规定正负，但弯矩图画在受拉侧。

在水平杆中， 当弯矩使杆件下部纤维受拉时为正。

A 端B 端杆端内力 F Q ABF N ABM AB正 F N BA F Q BAM BA 正2、内力的计算方法K截面法：截开、代替、平衡。

内力的直接算式(截面内力代数和法)=截面一边所有外力沿截面法线方向投影的代数和。

轴力FN外力背离截面投影取正，反之取负。

剪力F=截面一边所有外力沿截面切线方向投影代数和。

Q外力绕截面形心顺时针转动，投影取正，反之取负。

弯矩M =截面一边所有外力对截面形心的外力矩之和。

外力矩和弯矩使杆同侧受拉时取正，反之取负。

2、内力的计算方法【例】如图所示简支梁，计算截面C 、D 1、D 2的内力。

2m 4m 2mA2kN/mCBD 1 D 210kN0.2m10kN3.75kN0.25kN3、绘制内力图的规定内力图是表示结构上各截面的内力各杆件轴线分布规律的图形， 作图规定：弯矩图一律绘在受拉纤维一侧，图上不注明正负号；剪力图和轴力图可绘在杆轴线的任一侧(对水平杆件通常把正号的剪力和轴力绘于上方)，但必须注明正负号，且正负不能绘在同一侧。

求多跨静定梁的支座反力多跨静定梁是指由多个跨度组成的梁，在力学中属于静定结构，其支座反力的计算是工程设计中的重要环节。

本文将以多跨静定梁的支座反力为主题，介绍支座反力的计算方法和相关注意事项。

我们需要了解多跨静定梁的基本概念。

多跨静定梁由两个或多个跨度组成，每个跨度之间都有支点或支座连接。

在设计中，我们通常要求每个跨度的长度、截面形状和材料性质均相同，以便简化计算。

支座反力是指每个支点或支座上的反力，它们的大小和方向对梁的受力分布起着重要作用。

在计算多跨静定梁的支座反力时，我们需要考虑以下几个要点。

首先，梁的受力平衡条件必须满足。

根据力学原理，对于静定结构，支座反力和外力的合力必须为零。

因此，我们可以通过受力平衡方程来计算支座反力。

其次，由于多跨静定梁存在多个支点或支座，我们需要分别计算每个支点或支座上的反力。

最后，由于梁的受力分布是由支座反力决定的，因此支座反力的计算对于梁的结构和性能具有重要影响。

在计算多跨静定梁的支座反力时，我们可以采用不同的方法。

其中一种常用的方法是力法。

力法是一种基于力平衡原理的计算方法，它通过假设每个支点或支座上的反力大小和方向来建立受力平衡方程，然后利用这些方程求解未知量。

另一种常用的方法是位移法。

位移法是一种基于位移相容性原理的计算方法，它通过假设梁的位移和变形情况来建立位移相容性方程，然后利用这些方程求解未知量。

无论采用哪种方法，我们都需要根据具体情况选择合适的计算方法，以确保计算结果的准确性和可靠性。

在进行多跨静定梁的支座反力计算时，我们还需要注意以下几个问题。

首先，要正确确定梁的边界条件和受力情况。

边界条件包括支点或支座的固定方式和约束条件，受力情况包括外力的大小、方向和作用点。

其次，要考虑梁的自重和荷载对支座反力的影响。

自重是指梁本身的重量，荷载是指施加在梁上的外力。

对于多跨静定梁来说，自重和荷载的分布是不均匀的，因此我们需要根据具体情况对其进行合理估计和计算。

支座反力计算简单的静定结构可以通过力的平衡和力矩的平衡来建立两个方程式,每个方程是可以求一个未知量,就是说,简单的静定结构只能求两个未知力；对于超静定结构计算就复杂了,不过还是要用到平衡和力矩的平衡来建立方程,此外根据具体的情况增加其他方程联合求解,就是说,有多少个未知力就需要多少个方程式；例如：一条简支梁长为L,两头AB简支,从左到右在1/3L处有个P向下的集中力,求两端支座反力;这就是简单的静定结构,解题如下：设两端的支座反力分别为：Ra和Rb根据垂直方向力的平衡条件得：Ra + Rb = P根据垂直方向力矩的平衡条件,以A为原点,得：RbL=P1/3L顺时针力矩等于逆时针力矩,A的支座反力过原点,力矩为零联立两个方程组解得：Ra =2/3PRb =1/3P图解在这里是用不上,所有结构力学的书都有计算的方法的,最好就是找来看看,比我们在这里费尽心思的讲解要好得多;例题：简支梁的支座反力计算杆件长5米,离A端头米有集中荷载为100N,问A,B两支座的反力为多少最佳答案RA=70KN RB=30KN1.1.5支座反力计算在静定结构的受力分析中,通常须预先求出支座反力,再进行内力计算;求支座反力时,首先应根据支座的性质定出支座反力包括个数和方位,然后假定支座反力的方向,再由整体或局部的平衡条件确定其数值和实际指向;以图1-6a所示多跨刚架为例,讨论支座反力计算;图1-6此刚架有五个支座反力：、、、和;由整体的三个平衡方程,加上铰D和铰C处弯矩分别为零的平衡条件,即可求出这五个支座反力;从几何组成的角度看,D 以右部分为三铰刚架,是基本部分；D以左部分是支承在地基和三铰刚架上的附属部分;首先,取附属部分为隔离体图1-6b,由平衡方程求、和;a然后,将D铰处的约束反力反向加在基本部分上,取D以右三铰刚架为隔离体图1-6c,利用平衡方程求和;bc再取C以右半刚架为隔离体图1-6d,由铰C处弯矩为零的平衡方程求;d最后,由三铰刚架ABC第三个整体平衡方程求;e。