当前位置：文档之家 › 实验八 非线性控制系统分析

实验八 非线性控制系统分析

  • 格式：doc
  • 大小：867.00 KB
  • 文档页数：5

下载文档原格式

  / 5

合集下载

自动控制原理非线性控制系统分析

自动控制原理非线性控制系统分析
M -a
y
0
a
x
-M
y M7
2、死区特性 当输入|x|≤ ∆ 时，输出y=0，当输入|x|> ∆ 时，y与x呈线性关系。∆ 死区范围，K=tgβ 是死 区特性线性段的斜率。
死区特性对系统最直接的影响是造成系统的 稳态误差。死区的存在相当于降低了系统的开环 增益，从而提高了系统的稳定性，减弱了过渡过 程的振荡性。另外死区可以滤除输入端做小幅度 振荡的干扰信号，从而提高系统的抗干扰能力。
81非线性控制系统概述研究非线性控制理论的意义实际上理想的线性系统并不存在组成系统的各元件的动态和静态特性都存在着不同程度的非线性
自动控制原理
第八章 非线性控制系统分析
8-1 非线性控制系统概述
1. 研究非线性控制理论的意义
实际上，理想的线性系统并不存在，组成 系统的各元件的动态和静态特性都存在着不同 程度的非线性。
y M -a K 0 a -M x
13
8
3、饱和特性 当输入|x|≤ a 时， y与x呈线性关系， 即y=Kx；当输入|x|> a时，输出y保持为 一常值 。a为线性区，K是饱和特性线性 区的斜率。 饱和特性对系统的影响比较复杂，随 系统的结构和参数的不同而不同。但一般 来说，饱和特性往往促使系统稳定，但会 减小系统的放大系数，降低系统的稳态精 度。
y y y
0
x
0
x
0
x
3
2. 非线性系统的特征 稳定性分析复杂，系统可能存在多个平衡状态； t x0 e x x( x 1) x(t ) 1 x0 x0 et
4
可能存在自激振荡现象； 频率响应发生畸变。
3. 非线性系统的分析与设计方法

自动控制原理第八部分非线性控制系统分析

自动控制原理第八部分非线性控制系统分析

8.2 常见非线性特性及其对系统运动的影响
在一个控制系统中,包含有一个以上的非线性元件，
就构成了非线性系统。 控制系统中的典型非线性特性有：
8.2.1 饱和特性 饱和非线性的输入输出关系及数学表达式如下：
xa ka y kx x a ka x a
对系统的影响：
y
上的斜率应大小相等，符号相同。
( x , x )
x
图8-15
相轨迹对称于原点
f ( x, x ) f ( x, x )
(8-14)
2.相平面上的奇点
由相轨迹的斜率方程
x dx dx f ( x, x) 可知,相上的
点
只要不同时满足x 0, f ( x, x ) 0 ( x, x )
例8-1.设系统的微分方程为：
x
x x 0 x
其相平面图如右图所示 （绘制方法在下节介绍）
D
0
E
C
图中的箭头表示系统的 状态沿相轨迹的移动方向。
1 A B
x
p
图8-9 例8-1的相平面图
18
由图可知： （1）在各种初始条件下（任意一条相轨迹），系统都趋向原点（0,0）,说 明原点是系统的平衡点，系统是稳定的。
f ( x, x )
x(t), 也可以写成以t为参变量的形式，用 这个 来表示。
x f (x )
x(t)
x
x
t 图8-8 方程的解
1.相轨迹：如果我们取 x 和 作为平面的直角坐标，则 x 系统在每一时刻的 均相应于平面上的一点。当 t 变化时， ( x, x ) 这一 点 x x 平面上将绘出一条相应的轨迹-----相轨迹。 在 它描述系统的运动过程。 2.相平面: x 平面称为相平面。对于一个系统，初始条件 x 不同时，其方程的解也不同。因而针对不同的初始条件，可以绘出不同的相轨迹。 若以各种可能的状态作为初始条件，则可得到一组相轨迹族。

非线性控制系统分析

非线性控制系统分析

2.
所谓自持振荡是指没有外界周期变化信号的作用时，系统内部产生的具有固 定振幅和频率的稳定周期运动。线性系统的运动状态只有收敛和发散，只有在临 界稳定的情况下才能产生周期运动，但由于环境或装置老化等不可避免的因素存 在，使这种临界振荡只可能是暂时的。而非线性系统则不同，即使无外加信号， 系统也可能产生一定幅度和频率的持续性振荡，这是非线性系统所特有的。
按非线性环节的物理性能及非线性特性的形状划分，非线性特性有死区 特性、饱和特性、间隙特性和继电器特性等。
典型非线性特性
yபைடு நூலகம்
－a
0a
x
(a) y
－a
0a
x
(c)
y
－a
0
a
x
(b ) y
M
－a －ma 0 ma a x
－M (d )
1. 死区特性
死区又称不灵敏区，通常以阈值、分辨 率等指标衡量。
常见于测量、放大元件中，一般的机械系统、电机等，都不同程度地存在 死区。其特点是当输入信号在零值附近的某一小范围之内时，没有输出。只有 当输入信号大于此范围时，才有输出。 执行机构中的静摩擦影响也可以用死区 特性表示。控制系统中存在死区特性，将导致系统产生稳态误差，其中测量元 件的死区特性尤为明显。摩擦死区特性可能造成系统的低速不均匀，甚至使随 动系统不能准确跟踪目标。
k y f (x) xx
输出和输入呈非线性关系，其比值不是一个常数，可将其视为变增益比例环
节，常见非线性特性的等效增益曲线如图８-６(P390)。
二、常见非线性因素对系统运动的影响
非线性特性种类很多，且对非线性系统尚不存在统一的分析方法，所以 将非线性特性分类，然后根据各个非线性的类型进行分析得到具体的结论，才 能用于实际。

非线性控制系统的分析样本

非线性控制系统的分析样本

第八章非线性控制系统分析一、教学目与规定：通过对本章内容讲授，让学生结识到实际系统当中抱负线性系统并不存在，构成系统各元件，或多或少都存在着不同限度非线性，研究分析非线性系统办法十分必要，也很重要。

通过学习分析非线性系统相平面法和描述函数法，掌握分析非线性系统基本要领，规定学生能对某些常用非线性特性求描述函数，用描述函数办法分析非线性系统稳定性问题，极限环存在与消除；纯熟掌握二阶线性系统相轨迹各种形状，掌握非线性系统相平面分析办法。

二、授课重要内容：1．非线性控制系统概述1）非线性控制系统特点2）非线性控制系统分析办法2．常用非线性特性及其对系统运动影响1．相平面法1）相平面基本概念2）相轨迹绘制等倾线法1）线性系统相平面分析2）非线性系统相平面分析2．描述函数法1）描述函数基本概念2）典型非线性特性描述函数3）非线性系统稳定性分析描述函数法（详细内容见讲稿）三、重点、难点及对学生规定（掌握、熟悉、理解、自学）1.掌握什么是非线性系统、非线性系统特点、一阶线性近似化办法。

2.理解描述函数概念及计算办法，掌握非线性系统描述函数分析法。

3.掌握相轨迹绘制办法、线性二阶系统相轨迹及奇点分析以及非线性系统相平面分析办法。

4.理解李亚普诺夫各类稳定性定义及鉴定办法。

四、重要外语词汇非线性控制系统 nonlinear control system相平面法 phase-plane method描述函数法 description function method逆系统法 inverse system method等效增益 equivalent gain继电特性 relay characteristic死区特性dead band characteristic饱和特性 saturation characteristic间隙特性 clearance characteristic根轨迹 root locus相轨迹 phase locus奇点 odd nod奇线 odd line伪线性系统 fake linear system五、辅助教学状况（见课件）六、复习思考题1．什么是非线性系统？它有什么特点？2．常用非线性特性有哪些？3．非线性系统分析设计办法有哪些？4．描述函数分析法实质是什么？试述描述函数概念及其求取办法。

《自动控制原理》第八章非线性控制系统分析

《自动控制原理》第八章非线性控制系统分析

K G jw = ( ) S 0.1S+1)( 0.2S+1) ( K −0.3w− j(1−0.02w2 )] [ = 4 2 w 0.0004w + 0.05w +1) (
S= jw
令 ImG(jw) = 0 即 1 – 0.02w2 = 0 ，可得 G(jw) 曲线与负实轴交点的频率为：
1 wx = = 50 = 7.07rad / s 0.02
C(t)
∆2 ∆3 ∆ = ∆1 + + k k k2 1 1
K1 ，k2 ，k3 为传递函数各自的增益
处于系统前向通路最前边的元件，其死区所 造成的影响最大，而放大元件和执行元件的影响 可以通过提高这些元件前几项的传递函数来减小。 死区对系统的直接影响是造成稳态误差，降 低了定位精度。
≤ 时，输出量 y 与 x 是线 饱和：当输入量 x≤ a x> a > 时，输出量不再 性关系 y = kx ，当 随着输入量线性增长，而保持为某一常值。
两条曲线在交点处的幅值相等，即： −π
1 1 1 2 [arcsin + 4 1−( ) ] A A A = −1
得：A = 0.5 应用奈氏判据可以判断交点对应的周期运动 2.5sin7.07t 是稳定的，故当 k = 15 时，非线性系统 工作在自振状态，自振振幅 A = 2.5 ，频率 w = 7.07rad/s （2）欲使系统稳定地工作，不出现自振荡，由于 G(s) 的极点均在右半平面，故根据奈氏判据
相对负倒描述函数为：
A A2 ( ) 1 π π h h − =− =− NA ( ) 4 4 A2 h2 1−( ) ( ) −1 h A
采用相对描述函数后，系统的特征方程改写为：

自动控制原理第八章非线性控制系统分析

自动控制原理第八章非线性控制系统分析

第八章非线性控制系统分析l、基本内容和要求（l）非线性系统的基本概念非线性系统的定义。

本质非线性和非本质非线性。

典型非线性特性。

非线性系统的特点。

两种分析非线性系统的方法——描述函数法和相平面法。

（2）谐波线性化与描述函数描述函数法是在一定条件下用频率特性分析非线性系统的一种近似方法。

谐波线性化的概念。

描述函数定义和求取方法。

描述函数法的适用条件。

（3）典型非线性特性的描述函数（4）用描述函数分析非线性系统非线性系统的一般结构。

借用奈氏判据的概念建立在奈氏图上判别非线性反馈系统稳定性的方法，非线性稳定的概念，稳定判据。

（5）相平面法的基本概念非线性系统的数学模型。

相平面法的概念和内容。

相轨迹的定义。

（6）绘制相轨迹的方法解析法求取相轨迹；作图法求取相轨迹。

（7）从相轨迹求取系统暂态响应相轨迹与暂态响应的关系，相轨迹上各点相应的时间求取方法。

（8）非线性系统的相平面分析以二阶系统为例说明相轨迹与系统性能间的关系，奇点和极限环的定义，它们与系统稳定性及响应的关系。

用相平面法分析非线性系统，非线性系统相轨迹的组成。

改变非线性特性的参量及线性部分的参量对系统稳定性的影响。

2、重点（l）非线性系统的特点（2）用描述函数和相轨迹分析非线性的性能，特别注重于非线性特性或线性部分对系统性能的影响。

8-1非线性控制系统分析1研究非线性控制理论的意义实际系统都具有程度不同的非线性特性，绝大多数系统在工作点附近，小范围工作时，都能作线性化处理。

应用线性系统控制理论，能够方便地分析和设计线性控制系统。

如果工作范围较大，或在工作点处不能线性化，系统为非线性系统。

线性系统控制理论不能很好地分析非线性系统。

因非线性特性千差万别，无统一普遍使用的处理方法。

非线性元件(环节)：元件的输入输出不满足(比例+叠加)线性关系，而且在工作范围内不能作线性化处理(本质非线性)。

非线性系统：含有非线性环节的系统。

非线性系统的组成：本章讨论的非线性系统是，在控制回路中能够分为线性部分和非线性部分两部分串联的系统。

08非线性控制系统分析

08非线性控制系统分析
1
2
第八章、非线性控制系统分析
本章主要内容：
一、非线性控制系统概述 二、常见非线性特性及其对系统运动的影响 三、相平面法 四、描述函数法 五、非线性控制的逆系统方法
3
第八章、非线性控制系统分析
本章要求 :
1、了解非线性系统的特点 2、掌握研究非线性系统相平面法 3、掌握研究非线性系统描述函数法 4、了解研究非线性系统的逆系统法
x
一、非线性控制系统概述(12)
必须指出，长时间大幅度的振荡会造成机械磨损，增加 控制误差，因此多数情况下不希望系统有自振发生。但在控 制中通过引入高频小幅度的颤振，可克服间隙、死区等非线 性因素的不良有影响。而在振动试验中，还必须使系统产生 稳定的周期运动。因此研究自振的产生条件及抑制，确定自 振的频率和周期，是非线性系统分析的重要内容。 （3）频率响应发生畸变 非线性系统的频率响应除了含有与输入同频率的正弦信 号分量（基频分量）外，还含有关于 的高次谐波分量， 使输出波形发生非线性畸变。若系统含有多值非线性环节， 输出的各次谐波分量的幅值还可能发生跃变。
描述函数法是基于频域分析法和非线性特性谐波线性化 的一种图解分析方法。
18
一、非线性控制系统概述(14)
描述函数法对于满足结构要求的一类非线性系统，通过 谐波线性化，将非线性特性近似表示为复变增益环节，然后 推广应用频率法，分析非线性系统的稳定性或自激振荡。 （3）逆系统法 逆系统法是运用内环非线性反馈控制，构成伪线性系统， 并以此为基础，设计外环控制网络。该方法应用数学工具直 接研究非线性控制问题，不必求解非线性系统的运动方程， 是非线性系统控制研究的发展方向。
4、间隙特性 齿轮、蜗轮轴的加工及装 配误差或磁滞效应是形成间隙 特性的主要原因。如下图所示。 间隙特性为非单值函数。

第八章 非线性控制系统分析

第八章 非线性控制系统分析

8.2 常见非线性特性及其对系统运动的影响
一、饱和特性 y 斜率k 斜率 -a 0 a x
x>a ka y = kx x ≤a − ka x < −a
对系统的影响： 对系统的影响： 1.使系统开环增益下降，对动态响应的平稳性有利； 使系统开环增益下降，对动态响应的平稳性有利； 使系统开环增益下降 2.使系统的快速性和稳态跟踪精度下降。 使系统的快速性和稳态跟踪精度下降。 使系统的快速性和稳态跟踪精度下降
3.逆系统法 逆系统法 运用内环非线性反馈控制，构成伪线性系统，并以 运用内环非线性反馈控制，构成伪线性系统， 此为基础，设计外环控制网络。该方法应用数学工具直 此为基础，设计外环控制网络。 接研究非线性控制问题，不必求解非线性系统的运动方 接研究非线性控制问题， 程，是非线性系统控制研究的发展方向。 是非线性系统控制研究的发展方向。
二、死区特性 y 斜率k 斜率 -△ 0
△
x
0 x ≤∆ y= k[ x − ∆sign( x)] x > ∆
对系统的影响： 对系统的影响： 1.使系统产生稳态误差； 使系统产生稳态误差； 使系统产生稳态误差 2.当系统输入端存在小扰动信号时，在系统动态过程的 当系统输入端存在小扰动信号时， 当系统输入端存在小扰动信号时 稳态值附近，死区的作用可减小扰动信号的影响。 稳态值附近，死区的作用可减小扰动信号的影响。
三、间隙特性 y c 斜率k 斜率 -h 0 h -c 对系统的影响： 对系统的影响：
k ( x − h) y = k ( x + h) x c sign ( x)
ɺ y>0 ɺ y<0 ɺ y=0
增大系统的稳态误差，降低系统的稳态精度， 增大系统的稳态误差，降低系统的稳态精度，使过 渡过程振荡加剧，甚至造成系统的不稳定。 渡过程振荡加剧，甚至造成系统的不稳定。 一般来说，间隙特性对系统总是有害的， 一般来说，间隙特性对系统总是有害的，应该消除 或消弱它的影响。 或消弱它的影响。

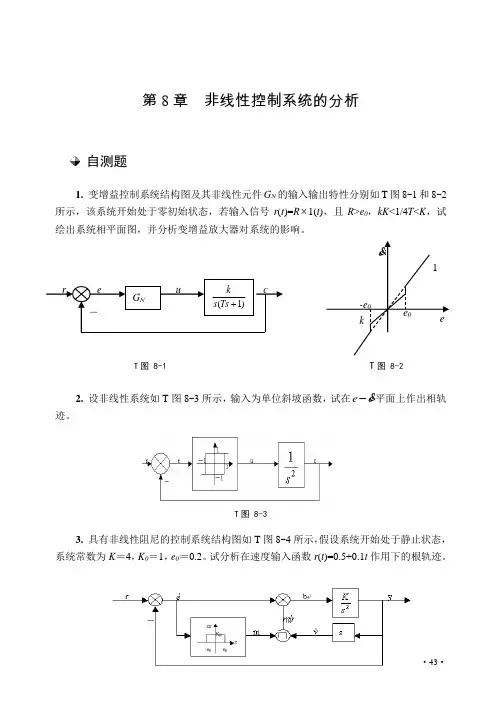
非线性控制系统的分析

非线性控制系统的分析

第8章非线性控制系统的分析自测题1. 变增益控制系统结构图及其非线性元件G N的输入输出特性分别如T图8-1和8-2所示，该系统开始处于零初始状态，若输入信号r(t)=R⨯1(t)，且R>e0，kK<1/4T<K，试绘出系统相平面图，并分析变增益放大器对系统的影响。

T图 8-1 T图 8-22. 设非线性系统如T图8-3所示，输入为单位斜坡函数，试在ee-平面上作出相轨迹。

T图 8-33.具有非线性阻尼的控制系统结构图如T图8-4所示，假设系统开始处于静止状态，系统常数为K＝4，K0＝1，e0＝0.2。

试分析在速度输入函数r(t)=0.5+0.1t作用下的根轨迹。

·43··44·yT 图 8-44. 非线性系统结构图如T 图8-5所示，a =0.5，K =8，T =0.5s ，K 1=0.5，要求：（1）当开关打开时，e (0)=2，0)0( e的相轨迹； （2）当开关闭合时，绘制相同初始条件的相轨迹，并说明测速反馈的作用。

T 图 8-55. 将T 图8-6和8-7所示非线性系统简化成典型结构形式，并写出线性部分的传递函数。

T 图 8-6T 图 8-76. 根据已知的非线性描述函数，求T 图8-8所示各种非线性的描述函数。

·45·(a) (b)T 图8-87. 已知系统的结构图如T 图8-9所示，K ＝4，M ＝1，k =1，r (t )=1(t )，c(0)=0，0)0(=c。

在e e - 平面上画出相轨迹，并画出c (t )的曲线，且说明运动情况(若有稳态误差，则计算其值，若有振荡，则计算振荡周期)。

T 图 8-98. 系统结构图如T 图8-10所示，试将其归化为一个非线性环节和一个线性部分串联的典型结构。

T 图 8-109. 在T 图8-11所示系统中，（1）确定使系统稳定的开环放大倍数K ； （2）分析滞环宽度h 对极限环工作周期的影响；·46·（3）试提出一个可实现的设计方案，使K 为确定数值（如K ＝10）时系统能稳定工作。

第8章非线性控制系统分析

第8章非线性控制系统分析

8.1 非线性系统的一般概念
非线性系统有许多特殊性能。当线性程度比较严重，本质 非线性，输入信号变化范围较大，或者需要研究系统中存在 的非线性现象, 以及特地应用非线性系统改善系统性能时， 上述线性研究方法就不适用了，必须应用非线性理论。
在多数情况下，固有的非线性特性将给系统的正常工作和 性能带来不利影响。但有时为了改善系统的性能，也会人为 地在系统中加入某些非线性特性。
值不固定。
其数学表达式为
y
k
(
x
asign
x)
b sign x
dy 0 dt dy 0 dt
• 饱和非线性的器件：
– 放大器的饱和输出特性、磁饱和、元件的行程限制、功率 限制等等。
饱和特性将使系统在大信号作用下之等效放大系数减小，因 而降低稳态精度。在有些系统中利用饱和特性做信号限幅y k(x ) x
k(x ) x
特征：当输入信号在零位附近变化时，系统没有输出。当输入
在线性系统中，系统输出的动态响应曲线形状与输入信号 大小无关，也与初始条件无关。 例如在图8-1所示线性系统中，阶跃输入不同幅值时，对 应线性系统输出响应曲线如图8-2和图8-3所示，响应曲 线形状相似。
图8-1线性系统
图8-2线性系统阶跃响应曲线R1 1,
图8-3线性系统阶跃响应曲线 R2 2
继电器非线性特性一般会使系统产生自持振荡，甚至 系统不稳定，并且使稳态误差增大 。
理想继电器（双位）
输出 输入
具有滞环的继电器
输出 输出
具有死区继电器
输入
输出
输入
输入
具有死区和滞环的继电器 包含有死区、饱和、滞环特性
4、间隙特性
间隙特性表现为正向与反向特性 不是重叠在一起，而是其输入— 输出曲线为闭合环路。其静特性 曲线如图8-18所示，其中 b

非线性控制系统的设计与分析研究

非线性控制系统的设计与分析研究

非线性控制系统的设计与分析研究随着科技的不断发展，非线性控制系统在各个领域中得到了广泛的应用。

非线性控制系统是指系统输出与输入之间的函数关系不满足线性可加性的一类系统，具有高度的复杂性和不确定性。

因此，对非线性控制系统进行设计和分析是非常必要的。

一、非线性控制系统的特点在非线性控制系统中，系统输出与输入之间的函数关系不满足线性可加性。

因此，非线性控制系统具有以下几个特点：1. 多变量交互作用非线性控制系统中的各个变量之间存在着复杂的交互作用关系，系统的输出不仅仅受到输入的影响，还受到其他因素的影响。

2. 多状态行为非线性控制系统中的系统行为非常复杂，其系统状态和输出呈现出多种不同的行为模式。

3. 非线性耦合非线性控制系统在变量之间存在非线性耦合关系，这会使得系统难以进行准确的建模、分析和控制设计。

二、非线性控制系统的设计在非线性控制系统的设计中，需要考虑以下几点：1. 建模对非线性控制系统的建模非常关键，建模的正确性直接影响到控制算法的准确性和效果。

2. 控制器设计针对具体的非线性控制系统，需要设计一种合适的控制器，使得系统可以做到稳定、高效地运行。

3. 状态观测器设计状态观测器是非线性控制系统中非常重要的一个组成部分，通过利用已知的系统输入和输出来估计未知的状态变量，从而提供给控制器使用。

因此，在非线性控制系统中，需要针对具体的系统设计合适的状态观测器。

三、非线性控制系统的分析在非线性控制系统的分析中，需要考虑以下几个方面：1. 稳定性分析稳定性是非线性控制系统中的一个重要问题，需要对系统进行稳态和瞬态的分析，以确定系统的稳定性。

2. 鲁棒性分析非线性控制系统在存在参数不确定性和外部干扰时，其控制效果会受到很大的影响。

因此，在非线性控制系统的设计和分析中，需要考虑其鲁棒性问题。

3. 性能分析性能是非线性控制系统中非常重要的一个指标，需要从控制系统的动态响应和控制误差等方面来进行分析和评估。

总之，非线性控制系统的设计和分析是非常重要的，需要从系统的建模、控制器和状态观测器的设计以及稳定性、鲁棒性和性能等多个方面进行综合考虑和分析。

非线性控制系统分析

非线性控制系统分析

8-2、常见非线性环节 教材P363图8-6
非线性环节的正弦响应
y(t) ωt y(t) ωt y(t) ωt y(t) ωt
8-3、相平面法 倒立摆例子
倒立摆杠子角度与角速率时间 响应
相轨迹（一个初态对应一条， 多个对应多条---相轨迹簇）
绘制---等倾线法
思想：先确定相轨迹的等倾线，进而绘出相轨迹的切 线方向场，然后从实始条件出发，沿方向场逐步绘制 相轨迹。 dx dx dx dx ) x x f ( x, x dt dx dt dx f ( x, x ) ) dx f ( x, x x dx x 斜率a取不同常数，相平面上得到多条等倾线，在
等倾线上各点处作斜率为a的短直线，并以箭头表示 切线方向，则构成相轨迹的切线方向场。步骤p360第 一段。
根与相轨迹
j λ 2 λ1 0 j 0 λ λ 1 2
0
稳定焦点
j 0
不稳定焦点
j λ1 0 λ2
中心
鞍点
（3）频率响应用发生畸变
二、分析与设计方法
（1）相平面法：（一阶二阶系统），通过 在相平面上绘制相轨迹曲线，确定非线性 微分方程在不同初始条件下解的运动形式。 （2）描述函数法：（高阶系统）满足条件 要求的一类非线性系统，通过谐波线性化， 近似表示为复变增益环节，应用频率法， 分析稳定性或自激振荡。
第八章 非线性控制系统分析
8-1、概述
理想的线性系统并不存在，因为组成控制系统 的各元件的动态和静态特性都存在不同程度的非线 性（例）。所以、实际系统中普遍存在非线性因素。 当系统中含有一个或多个具有非线性特性的元件时， 该系统称为非线性系统。 当非线性程度不严重时，运用小偏差线性化处理， 近似线性系统，采用线性系统方法分析和设计。严 重时，采用非线性处理方法。

实验八 非线性控制系统分析

实验八 非线性控制系统分析

实验八非线性控制系统分析【实验目的】1.掌握二阶系统的奇点在不同平衡点的性质。

2.运用Simulink构造非线性系统结构图。

3.利用Matlab绘制负倒描述函数曲线，运用非线性系统稳定判据进行稳定性分析，同时分析交点处系统的运动状态，确定自振点。

【实验原理】1.相平面分析法相平面法是用图解法求解一般二阶非线性系统的精确方法。

它不仅能给出系统稳定性信息和时间特性信息，还能给出系统运动轨迹的清晰图像。

设描述二阶系统自由运动的线性微分方程为分别取和为相平面的横坐标与纵坐标，并将上列方程改写成上式代表描述二阶系统自由运动的相轨迹各点处的斜率。

从式中看出在及，即坐标原点(0,0)处的斜率。

这说明，相轨迹的斜率不能由该点的坐标值单值的确定，相平面上的这类点成为奇点。

无阻尼运动形式()对应的奇点是中心点；欠阻尼运动形式()对应的奇点是稳定焦点；过阻尼运动形式()对应的奇点是稳定节点；负阻尼运动形式()对应的奇点是不稳定焦点；负阻尼运动形式()对应的奇点是不稳定节点；描述的二阶系统的奇点(0,0)称为鞍点，代表不稳定的平衡状态。

2.描述函数法设非线性系统经过变换和归化，可表示为非线性部分与线性部分相串联的典型反馈结构如图所示。

从图中可写出非线性系统经谐波线性化处理线性化系统的闭环频率响应为由上式求得图中所示非线性系统特征方程为，还可写成其中称为非线性特性的负倒描述函数。

若有使上式成立，便有或，对应着一个正弦周期运动。

若系统扰动后，上述周期运动经过一段时间，振幅仍能恢复为，则具有这种性质的周期运动，称为自激振荡。

可见自激振荡就是一种振幅能自动恢复的周期运动。

周期运动解 可由特征方程式求得，亦可通过图解法获得。

由等式在复数平面上分别绘制曲线和曲线。

两曲线的交点对应的参数即为周期运动解。

有几个交点就有几个周期运动解。

至于该解是否对应着自激振荡状态，取决于非线性系统稳定性分析。

【实验内容】 1. 相平面分析法（1）二阶线性系统相平面分析不同奇点的性质 例8-1 设一个二阶对象模型为 222()2nn nG s s s ωξωω=++绘制2,n ωζ=分别为0.5、-0.5、1. 25、0时系统的相平面图及24()4G s s =-的相平面图。

第八章 非线性控制系统分析

第八章 非线性控制系统分析
0

Y1 A B B1 1 1 A 1 tg 0 B1
2 1 2 1
Y1 B1 N( A) 1 A A 2 K sin 1 S S 1 S A A A (A S)

2

1.0
0.9 0.8 0.7 0.6
N( A) K
谐波线性化 设非线性系统的方框图如图2所示。 图中N（A）为非线性元件。设N（A）的输入信号为 一正弦信号x(t ) Asin t 由于非线性特性的作用，其 输出信号的稳态分量y（t）是一个非正弦周期函 数，其周期与输入信号相同。我们作如下假设： （1）高次谐波的幅值通常要比基波的幅值小； （2）系统的线性部分G(s)又具有低通滤波特性； 所以可以认为只有基波分量沿闭环回路反馈到N 的 输入端，而高次谐波经低通滤波后衰减得可以忽略 不计。在这种假设条件下，可以只考虑y的基波分 量。此外，设非线性特性为对称型。
2 2 B1 jA1 Y1 A1 B1 1 A1 N( A) 1 tg A A A B1
描述函数N(A)表示当非线性元件的输入信号为正 弦函数时，输出信号的基波分量与输入信号在幅 值和相位上的相互关系，类似于线性系统中的频 率特性。 在一般情况下，N(A)为正弦输入信号幅值的函数， 而与频率无关。当非线性元件的特性单值特性时， 其撤述函数是一个实数，这时输出信号基波与正 强输入信号同相。需强调指出，描述函数中相移 是由于非线性元件的非单位特性引起的，与线性 系统的频率特性中相移不是一回事。
x (t )
b
a

0
k
e (t )
a

b
继电器特性
由于继电器吸上电压和释放 电压的不同，其特性中包含了死区、回环和饱 和特性(图1(d))。图中当a＝0时的特性称为理 想继电器特性。在控制系统中，有时利用继电 器的切换特性来改善系统的性能。

自动控制原理第8章 非线性系统分析

自动控制原理第8章 非线性系统分析

一、 相平面的基本概念
设二阶非线性系统的微分方程为：
x f (x, x) 0
若令 x1 x, x2 x 则二阶系统可写成两个一阶微分方程，即

x1 x2

x2
f
(
x1,
x2
)
dx2 f ( x1, x2 )
dx1
x2
1.相平面，相点和相轨迹
以 x1 为横坐标，x2 为纵坐标的平面称为相平面， 相应的分析法称为相平面法；

x1 x2

x x
x1 x2

x2

f ( x1, x2 )
一般形式为


x1


f1( x1, x2 )
x2 f2 ( x1, x2 )
消去时间变量t，得到相轨迹的斜率方程
dx2 f2 ( x1, x2 ) dx1 f1( x1, x2 )
求解可得相轨迹方程，即
奇点为坐标原点,称 为不稳定焦点。
图8-4 -1＜＜0
时的相轨迹
(b) ＜-1时，特征根 是两个正实根，响应为 单调发散，相轨迹是一 族从原点出发向外单调 发散的抛物线，如图所 示。奇点为坐标原 点，称为不稳定节点。
图 8-5 ＜-1时的相轨迹
(c)对图所示的正反馈二阶系统
r(t)



n2 x1
相轨迹的斜率方程为:
dx2 2n x2 n2x1
dx1
x2
系统的奇点(平衡点)满足
dx2 0 dx1 0
解得 x1 0, x2 0 为系统的奇点。
系统的特征根为
1，2 -n n 2-1
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

实验八非线性控制系统分析
【实验目的】
1.掌握二阶系统的奇点在不同平衡点的性质。

2.运用Simulink构造非线性系统结构图。

3.利用Matlab绘制负倒描述函数曲线，运用非线性系统稳定判据进行稳定性分析，同
时分析交点处系统的运动状态，确定自振点。

【实验原理】
1.相平面分析法
相平面法是用图解法求解一般二阶非线性系统的精确方法。

它不仅能给出系统稳定性信息和时间特性信息，还能给出系统运动轨迹的清晰图像。

设描述二阶系统自由运动的线性微分方程为
分别取和为相平面的横坐标与纵坐标，并将上列方程改写成
上式代表描述二阶系统自由运动的相轨迹各点处的斜率。

从式中看出在及，即
坐标原点(0,0)处的斜率。

这说明，相轨迹的斜率不能由该点的坐标值单值的确定，相平面上的这类点成为奇点。

无阻尼运动形式()对应的奇点是中心点；
欠阻尼运动形式()对应的奇点是稳定焦点；
过阻尼运动形式()对应的奇点是稳定节点；
负阻尼运动形式()对应的奇点是不稳定焦点；
负阻尼运动形式()对应的奇点是不稳定节点；
描述的二阶系统的奇点(0,0)称为鞍点，代表不稳定的平衡状态。

2.描述函数法
设非线性系统经过变换和归化，可表示为非线性部分与线性部分相串联的典型反馈结构如图所示。

从图中可写出非线性系统经谐波线性化处理线性化系统的闭环频率响应为
由上式求得图中所示非线性系统特征方程为
，还可写成
其中
称为非线性特性的负倒描述函数。

若有
使上式成立，便有
或
，对应着一个正弦周期运动。

若系统扰动后，上述周期运
动经过一段时间，振幅仍能恢复为
，则具有这种性质的周期运动，称为自激振荡。

可见自激振荡就是一种振幅能自动恢复的周期运动。

周期运动解 可由特征方程式
求得，亦可通过图解法获得。

由等式在复数平面上分别绘制
曲线和
曲线。

两曲线的
交点对应的参数
即为周期运动解。

有几个交点就有几个周期运动解。

至于该解是
否对应着自激振荡状态，取决于非线性系统稳定性分析。

【实验内容】 1. 相平面分析法
（1）二阶线性系统相平面分析不同奇点的性质 例8-1 设一个二阶对象模型为 2
2
2
()2n
n n
G s s s ωξωω=
++
绘制2,n ωζ=分别为0.5、-0.5、1. 25、0时系统的相平面图及2
4()4
G s s =
-的相平面图。

图8-1 当2,0.5n ωζ==时，系统的单位阶跃响应曲线和相平面图
请同学们自己画出其他情况下系统的单位阶跃响应曲线和相平面图，并分析不同奇点的性质。

（2）用Simulink 分析非线性系统性能
例8-3 饱和非线性的控制系统如图8-3(a)所示，系统相轨迹的Simulink 仿真框图如图8-3(b)所示。

图8-3 (a) 系统方框图 图8-3 (b) 系统Simulink 仿真图
当K=15时系统的相轨迹如图8-4(a)所示，K=6时系统的相轨迹如图8-4(b)所示。

(a) K=15 (b) K=6 2.描述函数分析法
练习题
1. 用Simulink仿真，观察非线性系统的输入和输出。

（参考教材P251 例7-10）
2. 用Simulink仿真绘制教材P235例7-5中，当K=10时系统的相平面图。

提示：在前项通道中加入变增益模块Slider Gain ，通过改变增益，观察系统
3. 运用Matlab，使用描述函数法完成教材P248 例7-8和P249 例7-9的仿真，并判断自振点。

【实验要求】
1.掌握二阶系统的奇点在不同平衡点的性质。

2.运用Simulink构造非线性系统结构图。

3.学会运用Matlab绘制负倒描述函数曲线，巩固绘制线性系统Nyquist曲线的方法。

4.分析交点处系统的运动状态，确定自振点。

4. 实验心得.。