非线性控制系统分析

X X
这里，M=3，h=1
负倒描述函数为
N 1 X
X
12 1 1 2
X
X 1
X 1, N 1 X , N 1
必有极值
d N 1X 令
0 dX
得 X 2
N 1 2
2
0.523
12
1
1 2
2
6
X： 1 2
-N-1(X)： 0.523
2.自振的稳定性分析
在A点，振幅XA，频率A。
扰动：
X : A点 C点 C点被G(j)轨迹包围，不稳定，
振幅 ，工作点由C点向B点运动；
A点一个不稳 定的极限环。
X : A点 D点 D点不被G(j)轨迹包围，稳定，
振幅 ，工作点由D点左移。
在B点，振幅XB，频率B 。 扰动：
X : B点 E点 E点不被G(j) 轨迹包围，稳定，
振幅 ，工作点由E点到B点；
X : B点 F点 F点被G(j)轨迹包围，不稳定，
振幅 ，工作点由F回到B点。
B点呈现稳定的自激振荡:振幅XB ,频率B。
3.闭环系统稳定性判别步骤
1）绘制非线性部分的负倒描述函数曲线和线 性部分的频率特性曲线。
2）若G(j)曲线不包围“-N-1(X)”曲线，则系统稳定。 若G(j)曲线包围“-N-1(X) ”曲线，系统不稳定。 若G(j)曲线与“-N-1(X)”曲线相交，系统出现自振。
3）若G(j )曲线与“-N-1(X)”曲线有交点，做以 下性能分析：
（1）不稳定的极限环
（2）稳定的极限环 计算自振频率和幅值。
例1：非线性系统如图所示,其中非线性特性为 具有死区的继电器,分析系统的稳定性。
0e

解：1. 死去继电特性的描述函数
4M N(X)
1 ( )2
X
X
2. 绘制描述函数的负倒数特性
1
X
N(X ) 4M 1 ( )2
X
3. 绘制线性部分的极坐标图
4. 判断稳定性，分析两曲线相交点的性质
1 N(X)
X
-1.56 300 400 B -1 -0.5
X 130 A 140
120 G(j)
趋于奇点 远离奇点 包围奇点
例：二阶线性定常系统
••
•
x 2n x n2 x 0
试分析其奇点运动性质。
dx/dt x
稳定节点
••
•
x 2n x n2 x 0
dx/dt x
1
稳定节点
相轨迹趋于原点，该奇点称为 稳定节点
••
•
x 2n xn2 x 0
dx/dt x
1
不稳定节点
相轨迹远离原点，该奇点为 不稳定节点
者是自持振荡的
自持振荡点 a 振荡幅值=Xa
振荡频率=a
Im Re
X a
0
1 G(j) N ( X )
例：已知死区继电非线性系统如图
R(s)
+M
460
C(s)
+-
- -M
( j)(0.01 j 1)(0.005 j 1)
继电参数： M 1.7 死区参数：Δ 0.7 应用描述函数法作系统分析。
•
x
-1 -5/4
-3/2
-5/3
=
-2
-3/7
-3
-5 - x
3
1 1/3
0 -3/4 -1/2 -1/3

K G jw = ( ) S 0.1S+1)( 0.2S+1) ( K −0.3w− j(1−0.02w2 )] [ = 4 2 w 0.0004w + 0.05w +1) (
S= jw
令 ImG(jw) = 0 即 1 – 0.02w2 = 0 ，可得 G(jw) 曲线与负实轴交点的频率为：
1 wx = = 50 = 7.07rad / s 0.02
C(t)
∆2 ∆3 ∆ = ∆1 + + k k k2 1 1
K1 ，k2 ，k3 为传递函数各自的增益
处于系统前向通路最前边的元件，其死区所 造成的影响最大，而放大元件和执行元件的影响 可以通过提高这些元件前几项的传递函数来减小。 死区对系统的直接影响是造成稳态误差，降 低了定位精度。
≤ 时，输出量 y 与 x 是线 饱和：当输入量 x≤ a x> a > 时，输出量不再 性关系 y = kx ，当 随着输入量线性增长，而保持为某一常值。
两条曲线在交点处的幅值相等，即： −π
1 1 1 2 [arcsin + 4 1−( ) ] A A A = −1
得：A = 0.5 应用奈氏判据可以判断交点对应的周期运动 2.5sin7.07t 是稳定的，故当 k = 15 时，非线性系统 工作在自振状态，自振振幅 A = 2.5 ，频率 w = 7.07rad/s （2）欲使系统稳定地工作，不出现自振荡，由于 G(s) 的极点均在右半平面，故根据奈氏判据
相对负倒描述函数为：
A A2 ( ) 1 π π h h − =− =− NA ( ) 4 4 A2 h2 1−( ) ( ) −1 h A
采用相对描述函数后，系统的特征方程改写为：

x x
整理后得： x
2
x (x x )
2 2 0 2 0
相轨迹
2.等倾线法 --不解微分方程，直接在相平面上绘制相轨迹。 等倾线： 相平面上相轨迹斜率相等的诸点的连线。 等倾线法基本思想： 先确定相轨迹的等倾线，进而绘出相轨迹的切线 方向场，然后从初始条件出发，沿方向场逐步绘制相
四、继电特性
y M 0 x
M y M
x 0 x 0
-M
对系统的影响：
1可能会产生自激振荡，使系统不稳定或稳态误差增大；
2.如选得合适可能提高系统的响应速度。
其他继电特性
y
M -h 0 h -M x M -△ 0
y
-△
△
y M 0 △ -M x
-M
死区 + 继电
x
滞环 + 继电
x ，从x, x 中消
(2)直接积分法
dx dx dx dx x x dt dx dt dx
dx x f ( x, x ) dx
g ( x)dx h( x)dx

x
x0
g ( x)dx h( x)dx
x1,2 0.25 1.39 j
系统在奇点(0,0)处有一对具有负实部的共轭复根， 故奇点(0,0)为稳定的焦点。
f ( x, x ) 奇点(-2,0)处 x
x 2 x 0
2
f ( x, x ) x

c
c
c
c
(6)≤-1 s1s2 --两个正实根
四、奇点和奇线
1.奇点 --同时满足 x 0 和 f ( x, x) 0 的点。

法求解有困难时，可用图解法绘制。
▪ 对于式（9.2-1）xf(x,x)，令 x1x、 x2x ，
▪
有 x 2f(x1、 x2)，所以 可得 dx2 f (x1、x2)
d d x t2d dx x1 2d d x t1x2d dx x1 2f(x1、 x2)
（9.2-5）
▪
dx1
x2
式（9.2-5）是关于
y
-b 0
k
x
b
a.
b.
图9.1-4 齿轮传动及其间隙特性
y(x)k[xs g x)n b](|y/kx|b y (x)0、 y(x)C |y/kx|b
▪ 系统中若有间隙特性元件，不仅会使系统的输出产生相位滞后，导致 系统稳定裕量的减小，使动态性能恶化，容易产生自振；而且间隙区 会降低定位精度、增大非系线统性控静制差系统。的分析课件
▪ 由于相平面只能表示 x(t ) 和 x(t ) 两个独立变量，所以相 平面法只能用来研究一、二阶线性或非线性系统。
▪ 2）相轨迹的绘制方法
▪ （1）二阶线性系统的相轨迹 ▪ （2）相轨迹的绘制
非线性控制系统的分析课件
j
[s]
2 1
0
a.
j 1 [s]
0
2
d.
x2
j
x2
1
[s]
x1
0
0
0
稳定 节点
x
(
t
)
和 x (t ) 的一阶微分方程，即二阶非线性
系统的相轨迹方程。
▪
由式（9.2-5），令
dx2 f (x1,x2)
dx1
x2
，即有
▪
f (x1, x2 )
（9.2-6）

实验八非线性控制系统分析实验目的1.掌握二阶系统的奇点在不同平衡点的性质。

2.运用Simulink构造非线性系统结构图。

3.利用Matlab绘制负倒描述函数曲线，运用非线性系统稳定判据进行稳定性分析，同时分析交点处系统的运动状态，确定自振点。

实验原理1.相平面分析法相平面法是用图解法求解一般二阶非线性系统的精确方法。

它不仅能给出系统稳定性信息和时间特性信息，还能给出系统运动轨迹的清晰图像。

设描述二阶系统自由运动的线性微分方程为片+ 2冲+承=0分别取和为相平面的横坐标与纵坐标，并将上列方程改写成dx _24/ +曲H上式代表描述二阶系统自由运动的相轨迹各点处的斜率。

从式中看出在’「及—，即坐标原点（0,0）处的斜率灯‘以_门。

这说明，相轨迹的斜率不能由该点的坐标值单值的确定，相平面上的这类点成为奇点。

无阻尼运动形式（二--）对应的奇点是中心点；欠阻尼运动形式（「上」）对应的奇点是稳定焦点；过阻尼运动形式（―-）对应的奇点是稳定节点；负阻尼运动形式（：=二）对应的奇点是不稳定焦点；负阻尼运动形式-）对应的奇点是不稳定节点；■-描述的二阶系统的奇点（0,0）称为鞍点，代表不稳定的平衡状态。

2.描述函数法设非线性系统经过变换和归化，可表示为非线性部分「与线性部分，相串联的典型反馈结构如图所示。

从图中可写出非线性系统经谐波线性化处理线性化系统的闭环频率响应为ROM由上式求得图中所示非线性系统特征方程为■-，还可写成呛曲）=- ….或4丁 丁，对应着一个正弦周期运动。

若系统扰动后，上述周期运 动经过一段时间，振幅仍能恢复为 A 二：，则具有这种性质的周期运动，称为自激振荡。

可见自激振荡就是一种振幅能自动恢复的周期运动。

周期运动解A 二：可由特征方程式求得，亦可通过图解法获得。

由等式 宀小在复数平面上分别绘制|」 曲线和；， 曲线。

两曲线的 交点对应的参数即为周期运动解。

有几个交点就有几个周期运动解。

至于该解是 否对应着自激振荡状态，取决于非线性系统稳定性分析。

非线性系统在不同初始
偏移下的自由运动
2011 秋
许燕斌
自动控制理论A
Lo o
4、线性系统在没有外作用时，周期运动只发生在临界情况，
而这一周期运动是物理上不可能实现的; 非线性系统，在没有外作用时，系统中完全有可能发生一 定频率和振幅的稳定的周期运动，如图所示，这个周期运 动在物理上是可以实现的，通常把它称为自激振荡，简称 自振。
自动控制理论A
Lo o
x
k [e(t ) e0 ], x(t ) 0 x (t ) k [e(t ) e0 ], x(t ) 0 bsigne(t ), x(t ) 0
b k
k
e0 -b
-e0
e
2011 秋
许燕斌
自动控制理论A
4、继电特性
2011 秋
许燕斌
自动控制理论A
8.1 非线性系统及其特点
一.实际系统中的非线性因素
Lo o
一些常见的非线性特性
2011 秋
许燕斌
自动控制理论A
Lo o
除上述实际系统中部件的不可避免的非线性因素 外，有时为了改善系统的性能或者简化系统的结 构，人们还常常在系统中引入非线性部件或者更 复杂的非线性控制器。 通常，在自动控制系统中采用的非线性部件，最 简单和最普遍的就是继电器。
2011 秋
许燕斌
自动控制理论A
Lo o
二、非线性系统的特点（与线性系统的区别）
1、线性系统满足叠加原理，而非线性控制 系统不满足叠加原理。
2011 秋
许燕斌
自动控制理论A
Lo o
2、在线性系统中，系统的稳定性只取决于系统的 结构和参数，对常参量线性系统，只取决于系统 特征方程根的分布，而和初始条件、外加作用没 有关系； 对于非线性系统，不存在系统是否稳定的笼统概 念。必须具体讨论某一运动的稳定性问题。非线 性系统运动的稳定性，除了和系统的结构形式及 参数大小有关以外，还和初始条件有密切的关系。

一般非线性
描述函数不仅适合于分段线性系统，也适合于一般
非线性系统，只要能求出非线性环节的描述函数。我们 举一个例子:
1 1 3 y x x 2 4
因为它是单值、奇对称的，A1
0, 1 0 ，先求出 y (t ) ：
1 1 3 3 y (t ) A sin t A sin t 2 4
n 1

A 0 Yn sin(n t n )
n 1
y (t ) A0 ( An cos n t Bn sin n t )
n 1

A 0 Yn sin(n t n )
n 1
1 2 式中：A0 y (t )d t 0 2 1 2 An y (t ) cos n td t
2 1 2 1
这意味着一个非线性元件在正弦输入下，其输出也是
一个同频率的正弦量，只是振幅和相位发生了变化。
这与线性元件在正弦信号作用下的输出具有形式上的 相似性，故称上述近似处理为谐波线性化。
描述函数法的定义：输入为正弦函数时，输出的基波分量 与输入正弦量的复数比。其数学表达式为
Y sin( t 1 ) Y1 N ( A) 1 1 A sin t A A12 B12 A arctan 1 A B1
y
B
C
0
C
x
B
(a)
死区特性 一般的测量元件、执行机构都具有不灵敏区特性。只有在输 入信号大到一定程度以后才会有输出。一般的机械系统、 电机等, 都不同程度地存在死区。这种只有当输入量超过 一定值后才有输出的特性称为死区特 性，如图b所示。
y
k
C
0
C
x
k

非线性系统的数学模型是非线性微分方程；但至今为止 非线性微分方程没有成熟的解法；
8.2 几种典型的非线性特性
饱和特性 死区特性 间隙特性 继电器特性 变增益特性
(1)饱和特性(如运算放大器，学习效率等)
1. 对系统而言，饱和特性往往促使系统稳 定，但会减小放大系数，从而导致稳定 精度降低。 2. 饱和特性的例子是放大器，许多执行元 件也具有饱和特性。例如伺服电机。 3. 实际上，执行元件一般兼有死区和饱和 特性。
y1 ( t )
4M

sin t
理想继电特性的描述函数：
4M N ( A) 0 A
一般继电特性的描述函数：
2M mh 2 h 2 2M h N ( A) 1 ( ) 1 ( ) j ( m 1) 2 A A A A ( A h)
可能不稳定—发散、衰减等
3. 自振运动— 非线性系统特有的运动形式，产生自持振荡 4. 发生频率畸变—频率响应的复杂性 — 跳频响应，倍/分频 响应，组合振荡
非线性控制系统的分析方法
小扰动线性化
非线性系统研究方法 仿真方法
全数字仿真 半实物仿真 相平面法 描述函数法 波波夫法 反馈线性化法 微分几何方法
h 0 理想继电特性： m 1 死区继电特性： m 1 纯滞环继电特性：
4M N ( A) A
4M h N ( A) 1 A A
2
2
4M 4 Mh h N ( A) 1 j A A2 A
一般而言,描述函数 N(A)是A的函数,与频率无关 非线性环节为单/非单值函数时,N(A)是实/复数,虚部为/不为0
在小误差信号时具有较小的增益，从而提高系统的相对稳定性。 同时抑制高频低振幅噪声，提高系统响应控制信号的准确度。

第一张
上一张 下一张 最后一张
结束授课
非线性系统响应还有其他与线性 系统不同的现象,无法用线性系统的 理论来解释。在一些情况下,引入某 些非线性环节,使系统获得比线性系 统更为优异的性能。实际上大多数智 能控制都属于非线性控制范畴。
应当明确指出的是：非线性系统 分析中不能使用叠加原理,也不能使用 线性系统分析中传递函数、频率特性 数学模型。
上一张 下一张 最后一张
结束授课
三、自持振荡
线性二阶系统只在阻尼比=0时给予阶跃作用，将产生周期性响应过程, 这时系统处于临界稳定状态。
实际上,一旦该系统参数发生微小变化,该周期性状态就无法维持,要么 发散至无穷大,要么衰减至零。
而非线性系统在没有外作用时,有可能产生频率和振幅一定的稳定周期 性响应。该周期响应过程物理上可实现并可保持,通常将其称为自持振荡或 自振荡,如下图所示。
但当系统的非线性特征明显且不能进行线性化处理时，就必须采用非 线性系统理论来分析。这类非线性称为本质非线性。
第一节 非线性系统的基本概念
如果一个控制系统包含一个或一个以上具有非线性特性的元件或环节, 则此系统即为非线性系统。
如系统不能进行线性化处理，或其时域响应不能用线性微分方程（一 般只能用非线性微分方程来描述,具有非线性数学模型）来描述,则称为非 线性系统，或称为本质非线性系统。这样的系统有以下特点：
如果自振荡的幅值在允许范围内, 按照李雅普诺夫关于稳定性的定义,系 统是稳定的。
自振荡是人们特别感兴趣的一个问 题,对它的研究有很大的实际意义。在 多数情况下,正常工作时不希望有振荡 存在,必须设法消除它。但在某些情况 下,特意引入自振荡,使系统有良好的稳 态、暂态性能。
第一张
上一张 下一张 最后一张

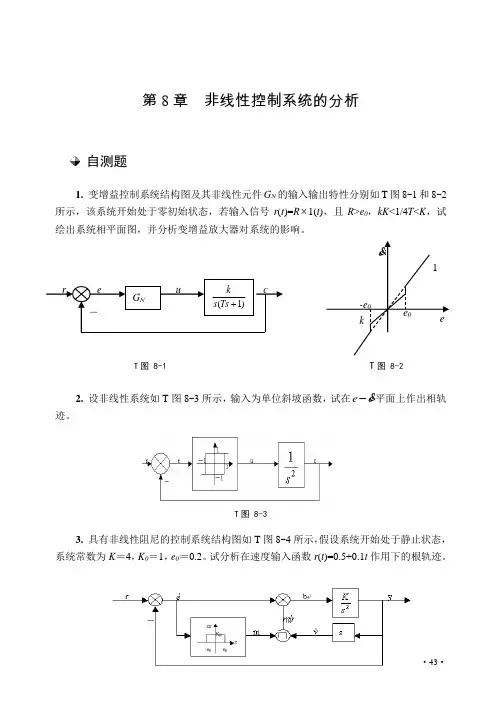
第8章非线性控制系统的分析自测题1. 变增益控制系统结构图及其非线性元件G N的输入输出特性分别如T图8-1和8-2所示，该系统开始处于零初始状态，若输入信号r(t)=R⨯1(t)，且R>e0，kK<1/4T<K，试绘出系统相平面图，并分析变增益放大器对系统的影响。

T图 8-1 T图 8-22. 设非线性系统如T图8-3所示，输入为单位斜坡函数，试在ee-平面上作出相轨迹。

T图 8-33.具有非线性阻尼的控制系统结构图如T图8-4所示，假设系统开始处于静止状态，系统常数为K＝4，K0＝1，e0＝0.2。

试分析在速度输入函数r(t)=0.5+0.1t作用下的根轨迹。

·43··44·yT 图 8-44. 非线性系统结构图如T 图8-5所示，a =0.5，K =8，T =0.5s ，K 1=0.5，要求：（1）当开关打开时，e (0)=2，0)0( e的相轨迹； （2）当开关闭合时，绘制相同初始条件的相轨迹，并说明测速反馈的作用。

T 图 8-55. 将T 图8-6和8-7所示非线性系统简化成典型结构形式，并写出线性部分的传递函数。

T 图 8-6T 图 8-76. 根据已知的非线性描述函数，求T 图8-8所示各种非线性的描述函数。

·45·(a) (b)T 图8-87. 已知系统的结构图如T 图8-9所示，K ＝4，M ＝1，k =1，r (t )=1(t )，c(0)=0，0)0(=c。

在e e - 平面上画出相轨迹，并画出c (t )的曲线，且说明运动情况(若有稳态误差，则计算其值，若有振荡，则计算振荡周期)。

T 图 8-98. 系统结构图如T 图8-10所示，试将其归化为一个非线性环节和一个线性部分串联的典型结构。

T 图 8-109. 在T 图8-11所示系统中，（1）确定使系统稳定的开环放大倍数K ； （2）分析滞环宽度h 对极限环工作周期的影响；·46·（3）试提出一个可实现的设计方案，使K 为确定数值（如K ＝10）时系统能稳定工作。

航天器控制系统
航天器控制系统是一个高度复杂的非线性控制系统，它涉及到轨道控制、姿态控制和推进系 统控制等多个方面。
航天器控制系统需要处理各种动态特性和非线性特性，如气动力、引力扰动和热效应等，以 确保航天器能够精确地完成预定任务。
航天器控制系统的设计需要运用非线性控制理论和方法，如自适应控制、鲁棒控制等，以提 高航天器的稳定性和精度。
非线性控制系统分析 教学课件
contents
目录
• 非线性控制系统概述 • 非线性控制系统的基本理论 • 非线性控制系统的分析与设计 • 非线性控制系统的应用实例 • 非线性控制系统的发展趋势与挑战
CHAPTER 01
非线性控制系统概述ห้องสมุดไป่ตู้
非线性控制系统的定义与特点
总结词
非线性、动态、输入与输出关系复杂
详细描述
反馈线性化方法是一种通过引入适当的反馈控制律，将非线性系统转化为线性系统的设 计方法。它通过调整系统的输入和输出，使得系统的动态行为变得线性化，从而可以利
用线性控制理论进行设计和分析。
滑模控制方法
总结词
一种用于处理非线性控制系统不确定性 的方法
VS
详细描述
滑模控制方法是一种通过设计滑模面和滑 模控制器，使得系统状态在滑模面上滑动 并达到期望目标的方法。它利用滑模面的 设计，使得系统对不确定性具有鲁棒性， 能够有效地处理非线性系统中的不确定性 和干扰。
非线性控制系统的基本理论
状态空间模型
状态空间模型是描述非线性控制系统动态特性的数学模型，由状态方程和输出方程 组成。
状态变量是描述系统内部状态的变量，输出变量是描述系统外部输出的变量。
建立状态空间模型需要考虑系统的非线性特性，包括死区、饱和、非线性函数等。

第八章非线性控制系统分析l、基本内容和要求（l）非线性系统的基本概念非线性系统的定义。

本质非线性和非本质非线性。

典型非线性特性。

非线性系统的特点。

两种分析非线性系统的方法——描述函数法和相平面法。

（2）谐波线性化与描述函数描述函数法是在一定条件下用频率特性分析非线性系统的一种近似方法。

谐波线性化的概念。

描述函数定义和求取方法。

描述函数法的适用条件。

（3）典型非线性特性的描述函数（4）用描述函数分析非线性系统非线性系统的一般结构。

借用奈氏判据的概念建立在奈氏图上判别非线性反馈系统稳定性的方法，非线性稳定的概念，稳定判据。

（5）相平面法的基本概念非线性系统的数学模型。

相平面法的概念和内容。

相轨迹的定义。

（6）绘制相轨迹的方法解析法求取相轨迹；作图法求取相轨迹。

（7）从相轨迹求取系统暂态响应相轨迹与暂态响应的关系，相轨迹上各点相应的时间求取方法。

（8）非线性系统的相平面分析以二阶系统为例说明相轨迹与系统性能间的关系，奇点和极限环的定义，它们与系统稳定性及响应的关系。

用相平面法分析非线性系统，非线性系统相轨迹的组成。

改变非线性特性的参量及线性部分的参量对系统稳定性的影响。

2、重点（l）非线性系统的特点（2）用描述函数和相轨迹分析非线性的性能，特别注重于非线性特性或线性部分对系统性能的影响。

8-1非线性控制系统分析1研究非线性控制理论的意义实际系统都具有程度不同的非线性特性，绝大多数系统在工作点附近，小范围工作时，都能作线性化处理。

应用线性系统控制理论，能够方便地分析和设计线性控制系统。

如果工作范围较大，或在工作点处不能线性化，系统为非线性系统。

线性系统控制理论不能很好地分析非线性系统。

因非线性特性千差万别，无统一普遍使用的处理方法。

非线性元件(环节)：元件的输入输出不满足(比例+叠加)线性关系，而且在工作范围内不能作线性化处理(本质非线性)。

非线性系统：含有非线性环节的系统。

非线性系统的组成：本章讨论的非线性系统是，在控制回路中能够分为线性部分和非线性部分两部分串联的系统。

第8章 非线性控制系统的分析重点与难点一、基本概念1. 线性与非线性系统的联系与区别控制系统在不同程度上都存在着非线性。

有些系统可以在工作点附近把它线性化，然后按线性系统来处理（如三级管放大器电路），但当系统含有本征非线性特性（如死区特性、继电器特性等）时，就不能用线性化的方法处理。

死区特性将使系统出现较大的稳态误差。

饱和特性将降低系统的超调量，有时还会引起稳定振荡。

间隙特性可使系统的振荡加剧，静差也会增大，有时会使系统不稳定。

继电器特性会出现低速爬行、蠕动及响应不平滑等现象。

与线性系统相比，非线性系统与线性系统的本质差别可以概括为以下三点： （1）线性系统可以使用叠加原理，而非线性系统不能使用叠加原理；（2）线性系统的稳定性与初值、输入无关，而非线性系统的稳定性与初值、输入有关； （3）线性系统可以写出通解形式，而非线性系统无法写出通解形式。

2. 相平面分析法以x ，x为坐标的平面就叫相平面，系统的某一状态对应于相平面上的一点。

相平面上的点随时间变化的轨迹叫相轨迹。

对应于二阶线性定常系统的相轨迹，可以对非线性系统进行分析，这种分析方法称为相平面分析法。

二阶线性定常系统的相轨迹如表8-1所示。

3. 极限环非线性系统存在着稳定的振荡状态，在相平面图上可表示为一个孤立的封闭相轨迹。

所有附近的相轨迹都渐近地趋向这个封闭的相轨迹，或离开该封闭的相轨迹，该相轨迹称为极限环。

极限环分为稳定和不稳定等四种形式，如表8-2所示。

非线性系统可能没有极限环，也可能存在多个极限环。

在相平面图形上，一个稳定的极限环就对应于一个自振状态。

4. 相平面做图法I —等倾线法令dx xd a / =，即),(x x f a =。

对于a 的不同取值，由),(x x f a =可得到x 与x 的不同关系式，而且在曲线),(xx f a =上，均具有相同的斜率a 。

给出一组a ，就可近似描绘出相平面图形。

表8-1 二阶线性系统022的相轨迹表8-2 极限环基本形式5. 相平面做图法II —δ方法给),(x x f x=两边同加x 2ω，得令 x x x f x x22),(ωω+=+ 22),(),(ωωδx x xf xx +=得 22),(ωδωx x x x=+ 因此 21212)(d x x=-+⎪⎭⎫ ⎝⎛δω式中 21122121111)( ),(δωδδ-+==x x d xx 利用上式就可得点],[11xx 邻域内的相平面图形。

否则，必须考虑死区的影响。而在工程实际中，有时为了提高系统的抗干扰能力，
会有意引入或增大死区。
3.间隙特性(滞环特性)
间隙特性的静特性曲线如图8.4所示，其数学表达式为
（8.3）
式中，a为间隙宽度，K为比例系数(线性段斜率)，(t)=dx(t)/dt。
ሶ
8.1
非线性控制系统概述
间隙特性是一种非单值特性，表现为正向特性与反向特性不是重叠在一起，而是在输入—输出曲线上出现
性具有明显的饱和非线性。
上述伺服电动机的非线性是因为使用的磁性材料具有非线性，
因此当输入电压超过一定数值时，伺服电动机的输出转矩就出现饱和现
象。实际上，由于伺服电动机还存在摩擦力矩和负载力矩，因此只有当
输入电压达到一定数值时，伺服电动机才会转动，即存在不灵敏区。所
以，伺服电动机的实际静特性是同时具有不灵敏区与饱和的非线性特性。
2.死区(不灵敏区)特性
死区特性的静特性曲线如图8.3所示，其数学表达式为
（8.2）
式中，a为死区宽度，K为线性输出斜率。
死区特性的特点是，当系统或环节有输入信号，但尚未超过数值a时，
无相应的信号输出。
死区特性在控制系统中也较为常见，一般的测量元件和执行机构都具
图8.3
死区特性
图8.4
间隙特性
有死区特性。当死区很小或对系统性能不会产生不利影响时，可以忽略不计。
现的这种周期运动即为自激振荡。自激振荡是非线性控制系统特有的，是非线性控制理论研究的重要问题。
8.1
非线性控制系统概述
8.1.4
非线性控制系统的分析与设计方法
描述非线性控制系统的基本数学模型是非线性微分方程，对非线性控制系统进行分析的重点是系统稳定性

非线性控制系统设计和分析一、引言非线性控制系统是一类关于非线性系统的控制理论，具有一定的广泛性和复杂性。

在现代控制理论中，非线性控制系统一直是研究的热点，得到了广泛的应用。

本文旨在探讨非线性控制系统的设计和分析方法，对其进行深入剖析和研究。

二、非线性系统的基本概念1.非线性系统的概念非线性系统指的是一个不满足线性叠加原理的动态系统，即其输入和输出之间的关系不是简单的比例关系。

在现实中的很多系统，如电机、飞行器、化学反应、金融市场等，都是非线性系统。

2.非线性系统的分类按照系统的状态和输入可以将非线性系统分为时变和时不变两类。

按照系统的动态特性可以分为不稳定、稳定和渐进稳定三类。

按照系统的性质可以分为连续和离散两类。

三、非线性系统的数学模型非线性系统的数学模型可以用微分方程、差分方程、偏微分方程等方式表示，采用状态方程、输入-输出方程、状态-输出方程等方式描述。

若系统的动态方程可以表示为：$$\frac{dx}{dt}=f(x,u)$$其中$f(x,u)$是非线性函数，则上式就是非线性系统的微分方程。

四、非线性控制系统的设计方法1.线性化设计法线性化是将非线性动态系统在一个操作点附近，通过Taylor级数展开为线性动态系统。

因此，线性化设计法可以将非线性动态系统的设计问题转化为线性动态系统的设计问题。

线性化方法主要有两种：一是状态反馈线性化法；二是输出反馈线性化法，两种方法可以互相转化。

线性化方法的优点是简单易行，缺点是受到线性化误差的影响。

2.非线性控制设计法非线性控制设计法是基于非线性系统控制理论进行的，包括经典的反馈线性化控制法、滑模控制法、自适应控制法、模糊控制法和神经网络控制法等。

反馈线性化控制法：反馈线性化法是一种将非线性系统转化为线性系统的控制方法，它通过反馈来改变系统的输入来实现控制。

反馈线性化控制法有很好的稳定性和鲁棒性。

滑模控制法：滑模控制法是一种常用的非线性控制方法，具有较好的容错能力和鲁棒性。

X (t ) f [ X (t ), U (t ), t ]
MATLAB与控制系统仿真实践， 北京航空航天大学出版社，2009.8. 在线交流，有问必答



在F与f函数中，如果相应的算子为线性， 则称为线性系统，否则称为非线性系统。 如果不显含t，则为时不变系统，若显含 t，则称为时变系统。 非线性系统输出暂态响应曲线的形状与 输入信号的大小和初始状态有关，非线 性系统的稳定性亦与输入信号的大小和 初始状态有关。非线性系统常会产生持 续振荡。
MATLAB与控制系统仿真实践， 北京航空航天大学出版社，2009.8. 在线交流，有问必答
本例给定输入为正弦信号，其幅值分别设为2、 4，其输出可以用示波器模块直接观察，也可 以输出到工作空间后，使用plot函数绘制。其 Simulink模型如图16.7。本例输出到工作空间 变量名设为simout，其保存格式设为Array， 在命令窗口使用plot函数绘制，运行结果如图。 >> plot(tout,simout(:,1),tout,simout(:,2))

3.设置仿真参数。如图16.10，将Solver options下的 Type项选为Fixed-step，Solver项选ode5(DormandPrince)，Fixed-step size 设为0.01。
MATLAB与控制系统仿真实践， 图16.10北京航空航天大学出版社， 仿真参数设置窗口 2009.8. 在线交流，有问必答
主要内容

原理要点 非线性系统概述 相平面法 描述平面法
MATLAB与控制系统仿真实践， 北京航空航天大学出版社，2009.8. 在线交流，有问必答
3. 描述函数法 非线性特性的描述函数法是线性部件频率特性在非线性特 性中的推广。它是对非线性特性在正弦信号作用下的输 出进行谐波线性化处理之后得到的，是非线性特性的一 种近似描述。 4. 用描述函数研究系统的稳定点的方法 用描述函数研究系统的稳定点的方法，是建立在线性系统 Nyquist稳定判据基础上的一种工程近似方法。其基本 思想是把非线性特性用描述函数来表示，将复平面上的 整个非线性曲线()理解为线性系统分析中的临界点，再 将线性系统有关稳定性分析的结论用于非线性系统。