下载文档原格式
工程力学中的静力学平衡方程在机械设计中的应用工程力学是研究物体在受力作用下的力学性质和工程问题的一门学科。
在工程力学中，静力学是最基础也是最重要的部分之一，而静力学平衡方程则是静力学的核心内容之一。
静力学平衡方程的应用广泛，特别是在机械设计中，它扮演着至关重要的角色。
下面，我们将重点探讨静力学平衡方程在机械设计中的应用。
一、静力学平衡方程的基本概念静力学平衡方程是根据力的平衡条件推导出的，它是描述物体在平衡状态下受力情况的数学表达式。
静力学平衡方程通常包括两个基本方程：合力平衡方程和力矩平衡方程。
合力平衡方程合力平衡方程是指物体在平衡状态下合力的矢量和等于零。
在机械设计中，我们通常需要考虑物体在水平方向和竖直方向上的合力平衡，即水平方向上的合力等于零和竖直方向上的合力等于零。
力矩平衡方程力矩平衡方程是指物体在平衡状态下力矩的矢量和等于零。
力矩是由力沿着某一轴线产生的力的旋转效果，力矩平衡方程可以用来描述物体在平衡状态下围绕某一轴线的力矩平衡。
二、静力学平衡方程在机械设计中的应用举例1.杠杆设计杠杆是一种常见的机械装置，利用杠杆原理可以实现力的放大或位置的变换。
在杠杆设计中，静力学平衡方程可以帮助我们确定杠杆的结构和参数。
例如，在设计一台起重机时，我们可以利用合力平衡方程和力矩平衡方程来确定起重机的平衡状态和工作条件。
2.支撑结构设计在机械设计中，支撑结构起到了关键的作用。
支撑结构的设计需要考虑到受力情况，而静力学平衡方程正是用来描述物体在平衡状态下受力情况的方程。
通过应用静力学平衡方程，我们可以计算出支撑结构所需的最小强度和稳定性要求，从而确保支撑结构的安全性和可靠性。
3.桥梁设计桥梁是工程力学中的重要研究对象之一。
桥梁设计要考虑到桥梁在受力情况下的平衡和稳定。
通过应用静力学平衡方程，我们可以确定桥梁结构在各种荷载条件下的受力情况，从而为桥梁的设计和建造提供重要的理论依据。
三、结语静力学平衡方程是工程力学中的重要内容，其在机械设计中的应用不可忽视。
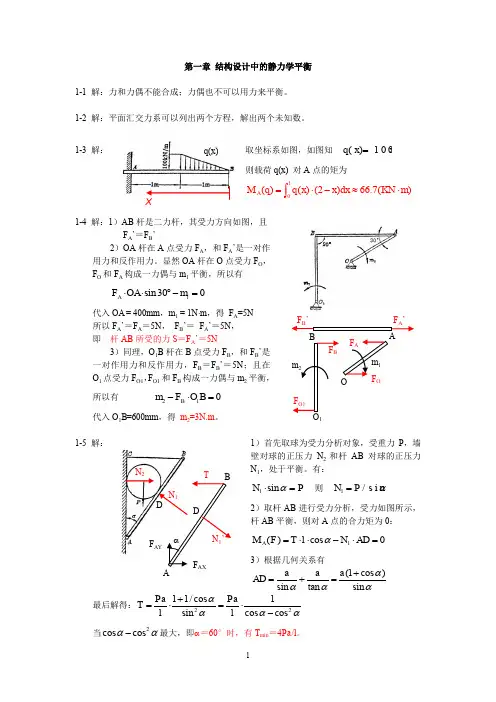
第一章 结构设计中的静力学平衡1-1 解：力和力偶不能合成；力偶也不可以用力来平衡。
1-2 解：平面汇交力系可以列出两个方程，解出两个未知数。
取坐标系如图，如图知 ()100q x x = 1-3 解：则载荷q(x) 对A 点的矩为1()()(2)66.7()A M q q x x dx KN m =⋅-≈⋅⎰1-4 解：1）AB 杆是二力杆，其受力方向如图，且 F A ’＝F B ’2）OA 杆在A 点受力F A ，和F A ’是一对作用力和反作用力。
显然OA 杆在O 点受力F O ，F O 和F A 构成一力偶与m 1平衡，所以有 1sin300A F OA m ⋅⋅︒-=代入OA = 400mm ，m 1 = 1N ⋅m ，得 F A =5N 所以F A ’＝F A ＝5N ， F B ’＝ F A ’＝5N ，即 杆AB 所受的力S ＝F A ’＝5N3）同理，O 1B 杆在B 点受力F B ，和F B ’是一对作用力和反作用力，F B ＝F B ’＝5N ；且在O 1点受力F O1，F O1和F B 构成一力偶与m 2平衡，所以有 210B m F O B -⋅= 代入O 1B =600mm ，得 m 2=3N.m 。
1-5 解：1）首先取球为受力分析对象，受重力P ，墙 壁对球的正压力N 2和杆AB 对球的正压力N 1，处于平衡。
有：1sin N P α⋅= 则 1/s i n N P α=2）取杆AB 进行受力分析，受力如图所示， 杆AB 平衡，则对A 点的合力矩为0： 1()cos 0A M F T l N AD α=⋅⋅-⋅=3）根据几何关系有(1cos )sin tan sin a a a AD αααα+=+=最后解得：2211/cos 1sin cos cos Pa Pa T l l αααα+=⋅=⋅- 当2cos cosαα-最大，即α＝60°时，有T min ＝4Pa/l 。
工程力学中的静力学平衡和动力学平衡的应用在工程领域中，静力学平衡和动力学平衡是两个至关重要的概念。
它们不仅是理论研究的基础，更是在实际工程应用中发挥着不可或缺的作用。
静力学平衡主要研究物体在静止状态下所受的力的关系。
当一个物体处于静止状态时，作用在它上面的所有力的合力为零，同时对于任何一个轴的力矩之和也为零。
这一原理在许多工程结构的设计和分析中被广泛应用。
比如在建筑工程中，桥梁的设计就是静力学平衡的典型应用。
桥梁需要承受自身的重量、车辆和行人的荷载等。
为了确保桥梁的稳定和安全，工程师必须精确计算各种力的大小和方向，并通过合理的结构设计使桥梁在这些力的作用下保持静力学平衡。
桥墩的位置和尺寸、桥梁的梁体结构等都需要经过精心设计，以保证力能够均匀分布，不会导致局部过载而发生破坏。
再看起重机械，如塔吊。
塔吊在吊起重物时，必须保证在静止状态下整个结构的稳定。
通过对塔吊各部分的受力分析，确定其重心位置、支撑点的强度以及吊臂的长度和承载能力等，从而保证塔吊在吊起不同重量的物体时都能保持静力学平衡，避免发生倾倒等危险情况。
在机械制造中，静力学平衡也同样重要。
例如，对于旋转机械的零部件，如飞轮、齿轮等，需要保证其在旋转过程中的质心与旋转轴重合，否则会产生离心力，导致振动和噪声增加，甚至会损坏零部件。
通过在设计和制造过程中进行静力学平衡的调整，可以有效地提高机械的性能和使用寿命。
动力学平衡则关注物体在运动状态下的力和运动的关系。
在动力学平衡中，物体所受的合力将导致物体产生加速度，而合力矩将导致物体的角加速度。
在汽车工程中，动力学平衡的应用十分广泛。
汽车的悬挂系统设计就是为了在行驶过程中保持良好的动力学平衡。
当汽车行驶在不平坦的路面上时，悬挂系统通过弹簧和减震器的作用，来平衡车轮所受到的冲击力，保证车身的平稳和轮胎与地面的良好接触，从而提高汽车的操控性和舒适性。
发动机内部的曲柄连杆机构也是动力学平衡的重要应用。
在发动机工作时，活塞的往复运动和曲柄的旋转运动都会产生惯性力和惯性力矩。
理论力学中的静力学平衡条件与应用在理论力学中，静力学是研究物体处于平衡状态时的力学原理和条件。
静力学平衡条件是判断物体是否处于平衡状态的基本准则。
本文将对理论力学中的静力学平衡条件进行分析，并探讨其在实际应用中的意义。
1. 刚体静力学平衡条件在理论力学中，刚体是指其形状和体积在外力作用下保持不变的物体。
刚体静力学平衡条件是判断刚体是否处于平衡状态的基本原理。
根据刚体静力学平衡条件，一个刚体处于平衡状态需要满足以下两个条件：- 力的平衡条件：合力为零。
即作用在刚体上的所有力的矢量和等于零。
- 力矩的平衡条件：合力矩为零。
即作用在刚体上的所有力矩的代数和等于零。
2. 非刚体静力学平衡条件在实际应用中，许多物体并不是刚体，而是由多个部分组成的弹性体。
对于非刚体的情况，同样存在静力学平衡条件来判断物体是否处于平衡状态。
非刚体静力学平衡条件包括以下几个方面：- 力的平衡条件：合力为零。
即作用在物体上的合外力等于零，物体保持静止。
- 力矩的平衡条件：合力矩为零。
即作用在物体上的合外力矩等于零，物体不会产生旋转。
- 形变平衡条件：物体内部各部分之间应满足力的平衡条件和形变的平衡条件，使得物体整体保持平衡。
3. 静力学平衡条件的应用静力学平衡条件在工程学、建筑学和力学等领域有着广泛的应用。
以下是一些典型的应用场景：- 结构力学：静力学平衡条件可用于判断建筑物、桥梁和机械结构等是否处于稳定的平衡状态，从而确保其安全性。
- 弹性体力学：静力学平衡条件可用于分析和设计材料的弹性性能，求解材料的应力和变形分布。
- 静力学问题求解：通过应用静力学平衡条件，可以解决一些静力学问题，如悬臂梁的荷载计算、桥梁上的力的平衡等。
4. 实例分析以建筑结构为例，应用静力学平衡条件可以分析房屋的支撑结构是否稳定。
在设计房屋的支撑结构时，需要考虑以下几个方面：- 力的平衡条件：房屋所受的重力需要通过支撑结构的柱子、墙壁等来承受，使得合力为零，保持平衡。
机械结构的强度及稳定性分析机械结构是指机械产品中各种零部件之间按一定方式相连接而成的整体。
机械结构主要是通过零部件之间的连接来承受机械负荷，因此其强度和稳定性都是至关重要的。
本文将从强度和稳定性两个方面来分析机械结构。
强度分析机械结构的强度分析是指对机械结构进行受力分析，以确定机械结构的承载能力，避免出现因受力不均匀引起的破坏事故。
根据机械工程基础知识，机械结构的受力分析主要分为以下几个方面：1. 静力学平衡静力学平衡是对机械结构进行的最基本的受力分析。
它是指当机械结构处于平衡状态时，各个力的合力为零。
在进行静力学平衡分析时，需要考虑外力和内力的作用，并通过受力分析图来表示各个受力成分的大小和方向。
2. 应力分析应力分析是指对机械结构在受到一定的力之后，各个零部件所承受的应力状态进行分析。
应力分析可以帮助设计师找到机械结构的受力集中点，并通过改变结构设计来提高机械结构的强度。
应力分析的常见方法有静应力法、动应力法、塑性分析法等。
3. 疲劳寿命分析疲劳寿命分析是指对机械结构在长时间振动或者受到变化载荷后，所承受的疲劳状态进行分析。
在进行疲劳寿命分析时，需要考虑机械结构的应力状态以及结构设计是否合理。
为了提高机械结构的疲劳寿命，需要减小应力集中点，采用材料强度高、抗疲劳性好的零部件等。
稳定性分析机械结构的稳定性分析是指对机械结构在受力状态下，能否保持平衡状态而不发生失稳的分析。
机械结构失稳后会导致其承受的荷载大大减小，进而导致破坏。
因此，在进行机械结构设计时，需要进行稳定性分析，以确保机械结构在受到荷载后能够保持平衡状态。
机械结构的稳定性分析主要有以下几个方面：1. 刚度分析刚度分析是指对机械结构的刚度进行分析。
机械结构的刚度越大，其稳定性就越好。
因此，在进行稳定性分析时，需要确保机械结构的刚度满足设计要求。
刚度分析的方法有有限元分析、分析法等。
2. 摩擦分析摩擦分析是指对机械结构摩擦力的影响进行分析。
静力学力的平衡与受力分析在物理学中，力是物体之间相互作用的结果，是描述物体受到的外界作用的量。
静力学力的平衡与受力分析是力学中的重要概念和方法。
本文将通过对静力学平衡和受力分析的讨论，阐述力的平衡条件以及如何进行受力分析。
静力学平衡的概念使我们能够了解物体在静止状态下所受的力的关系。
在一个封闭的系统中，如果物体保持静止，则该物体的受力和力的矩之和为零。
这可以用以下公式表示：ΣF = 0其中，ΣF表示所有作用在物体上的力的矢量和。
这个方程称为力的平衡条件，它是静力学平衡的基础。
平衡条件的主要应用在于解决各种物体和结构的受力问题。
通过对平衡条件的分析，我们可以确定物体上受力的大小、方向和作用点的位置。
在进行受力分析时，我们首先需要明确物体所处的受力系统。
受力系统包括物体所受的所有外力和内力。
外力是由外界环境对物体施加的力，如重力、摩擦力等。
内力是物体内部不同部分之间相互作用的力，如张力、弹力等。
确定了受力系统后，我们可以使用受力分析方法来计算物体所受力的大小和方向。
下面介绍几种常见的受力分析方法：1. 自由体图法：将物体从整体中分离出来形成自由体，只考虑物体受到的力，不考虑周围物体的作用。
通过绘制自由体图，我们可以清楚地看到物体所受的各个力的大小和方向，从而计算出受力平衡的条件。
2. 悬挂点法：对于悬挂在一定点上的物体，我们可以通过设定悬挂点作为坐标原点，建立力的平衡方程来求解物体所受的力。
通过受力分析，我们可以确定物体所受力的大小、方向和作用点的位置。
3. 斜面分解法：对于放置在斜面上的物体，我们可以将受力分解为平行和垂直于斜面的分力，通过受力分析得到物体所受力的大小和方向。
受力分析在工程学和物理学中有着广泛的应用。
它可以帮助我们解决各种实际问题，如桥梁的结构稳定性分析、机械装置的设计优化等。
除了上述介绍的受力分析方法，还有其他一些分析方法，如向量分解法、平衡方程法等。
不同的问题需要选择合适的受力分析方法，以便得到准确的结果。
静力学平衡的条件静力学平衡是物体处于力的作用下不发生平动和转动的状态。
在物体受到多个力的作用时，只有在满足一定的条件下，物体才能保持静力学平衡。
下面将详细介绍静力学平衡的条件以及其应用。
首先，我们来了解一下静力学平衡的基本概念。
在物理学中，力被定义为物体之间的相互作用，它可以使物体发生平动（直线运动）或旋转运动。
而静力学平衡是指物体在受到多个力的作用下，不发生平动或旋转运动，保持静止的状态。
要使物体处于静力学平衡，需要满足以下两个条件：1. 作用在物体上的合力为零：当物体受到多个力的作用时，合力是指所有力的矢量和。
如果作用在物体上的所有力的合力为零，即ΣF=0，那么物体将保持静止状态。
2. 作用在物体上的合力矩为零：力矩是指力绕固定点产生的转动效果。
当物体受到多个力的作用时，如果合力产生的力矩为零，即Στ=0，那么物体将不发生转动。
这两个条件是静力学平衡的基本要求，它们可以用数学方式表达为ΣF=0和Στ=0。
通过解这两个方程，我们可以得到物体处于静力学平衡时的各种力的大小和方向。
静力学平衡的条件不仅适用于简单的力学问题，也可以应用于复杂的工程和结构设计中。
例如，在建筑物和桥梁的设计中，静力学平衡的原理被广泛应用。
工程师需要通过计算各个部分受力的大小和方向，以保证结构的稳定和安全。
此外，静力学平衡的原理还可以用于解释一些日常生活中的现象。
例如，我们常见的平衡木就是基于静力学平衡的原理设计的。
当人站在平衡木上时，平衡木的两端受到相等大小的力，并且这些力的合力和合力矩均为零，从而使平衡木保持平衡。
同样的原理也适用于天平、摇摆椅等物体。
静力学平衡的条件不仅在物理学中有重要应用，在工程学和生活中也起着至关重要的作用。
它帮助我们理解物体静止和平衡的原理，并能够指导我们设计和构建稳定的结构。
总结起来，要使物体处于静力学平衡，必须满足作用在物体上的合力为零和合力矩为零的条件。
这些条件是静力学平衡的基本要求，我们可以通过解决这些条件得到物体受力的大小和方向。
精密机械设计基础四川大学制造学院 测控专业 2014.9Ⅰ 结构设计中的静力学平衡主讲：陆小龙参考文献n n n范钦珊，蔡新编著，《工程力学》，机械工业出版 社，2006.7 贾启芬，刘习军主编，《理论力学》，机械工业出 版社，2005.1 其他工程力学以及理论力学的相关书籍结构设计中的静力学平衡本章 重点 掌握静力学的基本概念和公理 Ø 掌握约束与约束反力的定义 Ø 学会绘制受力图 Ø 掌握摩擦自锁的原理Ø结构设计中的静力学平衡主要内容 静力学基本概念 n 静力学公理 n 约束与约束反力 n 受力图 n 平面一般力系的简化 n 平面一般力系的平衡 n 摩擦n 结构设计中的静力学平衡一、静力学基本概念一、静力学基本概念• • • •力是物体与物体之间相互的机械作用。
力的外效应：使物体的机械运动发生变化； 力的内效应：使物体产生变形。
力的三要素：力的大小、方向和作用点。
• 力是矢量: 力的单位是牛顿（N）或千牛顿 （KN） A B F结构设计中的静力学平衡一、静力学基本概念一、基本概念• 刚体：在受力情况下保持形状和大小不变的 物体。
（理想化了的力学模型）。
外力作用下物体视为刚体的情况： ①研究物体受力与运动关系时； ②由平衡条件求解物体所受外力时。
• 变形体：在研究物体受力与变形的关系时，认 为零件是弹性体。
• • 力系：同时作用在同一物体上的许多力。
力系分类：平面力系和空间力系 等效力系和平衡力系结构设计中的静力学平衡二、静力学公理二、静力学公理 公理1 力的平行四边形法则C B F2 O q FR a F1 A三角形法则FR O a F1 F2 AC作用在物体上同一点的两个力，可以合成一个合力。
合力的作用点仍在该点，合力的大小和方向由这两个力为 邻边所构成的平行四边形的对角线确定。
合力大小： 合力方位：FR = F12 + F22 + 2 F1 F2 cos qF2 sin q a = arctan F1 + F 2cos q二、静力学公理公理2 二力平衡公理 刚体仅受两个力作用而平衡的充分必要条件是：两个 力大小相等，方向相反，并作用在同一直线上。
FF该公理对刚体而言是必要与充分的，但对变形体而言 却只是必要而不充分。
二、静力学公理公理2 二力平衡公理 二力构件：仅受两个力作用而处于平衡的构件。
二力构件受力的特点是：两个力的作用线必沿其作用点的 连线。
下图中的三铰钢架中的BC构件，若不计自重，就 是二力构件。
二、静力学公理公理3 加减平衡力系公理 在作用于刚体上的已知力系上，加上或减去任一平衡 力系，并不改变原力系对刚体的作用效果。
注：加减平衡力系公理主要用来简化力系，仅适用于刚体。
推论1 力的可传性原理 作用于刚体上的力，可以沿其作用线移至刚体内任意一 点，而不改变该力对物体的作用效果。
力对刚体的效应与 力的作用点在其作用线上的位置无关。
因此作用于刚体上 的力的三要素是：力的大小、方向、作用线。
公理3 加减平衡力系公理推论2 三力平衡汇交定理若刚体受到同平面内三个互不平行的力的作用而平衡时，则该三个力的作用线汇交于一点。
F 1、F 2的合力F 3’与F 3平衡F 1F 2F 3F 3’A BC O公理4 作用和反作用定律作用力和反作用力总是大小相等，方向相反，作用线相同，但同时分别作用在两个相互作用的物体上。
表明：力总是成对出现的，只要有作用力就必有反作用力，而且同时存在，同时消失。
公理5 钢化原理变形体在某一力系作用下处于平衡，如将此变形体刚化为刚体，其平衡状态保持不变。
该公理提供了把变形体抽象为刚体模型的条件。
小结(1)1、静力学基本概念力的概念、力的内外效应、力的三要素。
刚体、变形体、力系、力系的分类。
2、静力学公理公理1：力的平行四边形法则公理2：二力平衡公理；二力构件？公理3：加减平衡力系公理？推论1：力的可传性原理推论2：三力平衡汇交定理公理4：作用和反作用定律公理5：钢化原理n主动力使机构运动或有运动趋势的力。
n 约束限制物体运动的条件。
n 约束反力约束限制构件运动而给构件的力。
F WF N1、柔性约束（柔索）柔性约束由绳索、胶带或链条等柔性物体构成。
只能受拉、不能受压。
只能限制沿约束的轴线伸长方向。
柔性约束对物体的约束反力是：作用在接触点、方向沿着柔体的中心线背离物体。
通常用F T表示。
F F T2F T1F 1F2 F1’F2’M1M2日光灯滑轮2、光滑面约束约束反力经过接触点沿光滑接触面的法线方向，指向物体，称为法向压力或正压力；不计摩擦。
F N F NA F NBAF WO BA3、光滑圆柱形铰链约束1）连接铰链两构件用圆柱形销钉连接且均不固定，即构成连接铰链，其约束反力用两个正交的分力F X和F Y 表示。
3、光滑圆柱形铰链约束2）固定铰链支座如果连接铰链中有一个构件与地基或机架相连，其约束反力仍用两个正交的分力F X 和F Y 表示。
YXF RYF R F RX3、光滑圆柱形铰链约束3）活动铰链支座在桥梁、屋架等工程结构中经常采用这种约束。
在铰链支座的底部安装一排滚轮，可使支座沿固定支撑面移动，这种支座的约束性质与光滑面约束反力相同，其约束反力必垂直于支撑面，且通过铰链中心。
FRAA4、固定端约束固定端约束能限制物体沿任何方向的移动，也能限制物体在约束处的转动。
所以，固定端A处的约束反力可用两个正交的分力F AX、F AY和力矩为M A 的力偶表示。
FMA A FXFY三、约束与约束反力5、球铰支座球铰链是一种空间约束，它能限制物体沿空间任何方向移动，但物体可以绕球心任意转动。
球铰链的约束反力可用三个正交的分力F AX、F AY和F AZ表示。
四、受力图画受力图是解决平衡问题的关键画受力图的一般步骤：（1）根据题意确定研究对象，并画出研究对象的分离体简图。
（2）在分离体上画出全部已知的主动力。
（3）在分离体上解除约束的地方画出相应的约束反力。
注：画受力图时要分清内力与外力，如果所取的分离体是由某几个物体组成的物体系统时，通常将系统外物体对物体系统的作用力称为外力，而系统内物体间相互作用的力称为内力。
内力总是以等值、共线、反向的形式存在，故物体系统内力的总和为零。
因此，取物体系统为研究对象画受力图时，只画外力，而不画内力。
ABFMA BFMF RAYF RAXF RBY小结(2)1、基本概念主动力、约束、约束反力的概念约束的类型：a.柔性约束b.光滑面约束c.光滑圆柱形铰链约束:连接铰链、固定铰链支座、活动铰链支座、固定端约束、球铰支座2、如何画受力图step1：根据题意确定研究对象，并画出研究对象的分离体简图step2：在分离体上画出全部已知的主动力step3：在分离体上解除约束的地方画出相应的约束反力。
n力对点之矩对平面力系工程上习惯逆时针为“＋”()o M F r F=×uu r u r r u r ()()o M F F d N m =±××OdFn合力矩定理平面力系的合力对平面内任一点的力矩等于各分力对同一点力矩的代数和。
R ()()o o i M F M F =åF R YAXOF 1F 2h 2h h 1aq bBC例1-3n力偶：大小相等、方向相反、不共线的两个相互平行的力。
n 力偶矩：M ＝±F ×d n 力偶矩的特点1、力偶对平面内任意点之力矩代数和等于力偶矩；2、力偶无合力(合力为0)，只能用力偶平衡；3、力偶等效变换性质。
d＋F F ’30N 2m20N3mM=60N ×m负力偶n平面力偶系的合成iM M =åF 2F 2d 2d 1F 1F 1’dF 3F 3’F 4’F d F R ’F Rn力的平移定理一个力可以平行于其作用线移到任意点，但必须附加一个力偶，这个力偶的矩等于原力对新作用点之矩，则其作用效果不变。
BAA BFB dF ”FF ’F ”MOA 1A 2A 3F 1’1n平面一般力系的简化任意一个平面力系总可以简化为一个主矢量R（作用于简化中心）和一个主矩M（等于力系各力对简化中心之矩的代数和）。
A 1A 2A 3F 1F 2F 3F 2’2F 3’3F 2’F 3’R Mn平面一般力系平衡的充要条件主矢量＝0，对任一点的主矩＝0平衡方程：ïþïýü=S =S =S 0)(000F M F F y x ïþïýü=S =S =S =S 000)(0)(y x B A F F F M F M 或ïþïýü=S =S =S 0)(0)(0)(F M F M F M C B A ïþïýü=S =S 00y x F F þýü=S =S 0)(00F M F y 一般工程A 、B 、C 三点不共线三个方程、三个未知数汇交力系平行力系or 例1－5小结(4)1、基本概念力矩、力偶、力偶的特点2、合力距定理R ()()o o i M F M F =å3、力的平移定理4、平面一般力系的简化5、平面一般力系平衡的充分必要条件n摩擦力产生条件：存在正压力，并有运动或运动趋势。
n有害面消耗部分功，降低效率；发热影响精度；磨损影响寿命。
n有利面摩擦传动、人行走；制动器；锁紧装置和螺纹紧固（自锁性）。
n滑动摩擦基本规律静摩擦力0 £Ff £Ffmax静摩擦定律F fmax = fFN静摩擦系数fFWFNF FfFRF Rn摩擦角n自锁主动力F 与法线夹角a <j n 自锁现象p25AF NF fF fmaxajmax N NNtan f F fF f F F j ===jj F Faa滚动摩擦自锁（补充）1.滚动摩擦自锁现象。
2.滚动摩擦自锁存在的条件。
3.滚动摩擦自锁与滑动摩擦自锁的比较。
4.滚动摩擦自锁的应用。
参见相关论文！滚动摩擦自锁（补充）滚动摩擦自锁的应用。
C例1-3n平面上作用两个平行力F 1与F 2。
已知F 1=30N，F 2=20N，d=400mm，试求合力F R 之大小、方向及作用线。
F 1F 2BA d OYXF Rd 1d 2例1－5n简易起重机如图，起重臂自重略去不计，求平衡时支座反力和绳子BC的张力。
B 30°ABC40°FWA40°30°FT1FNA1－Y2－XFWFT2FT2。
