第三章--静力学平衡

第三章 部分习题解答3-10 AB ,AC 和DE 三杆连接如图所示。

杆DE 上有一插销H 套在杆AC 的导槽内。

试求在水平杆DE 的一端有一铅垂力F 作用时，杆AB 所受的力。

设DE BC HE DH DB AD ===,,，杆重不计。

解：假设杆AB ，DE 长为2a 。

取整体为研究对象，受力如右图所示，列平衡方程：∑=0C M02=⋅a F By0=By F取杆DE 为研究对象，受力如图所示，列平衡方程：∑=0HM0=⋅-⋅a F a F DyF F Dy =∑=0B M 02=⋅-⋅a F a F DxF F Dx 2=取杆AB 为研究对象，受力如图所示，列平衡方程：∑=0y F0=++By Dy Ay F F FF F Ay -=(与假设方向相反)∑=0A M02=⋅+⋅a F a F Bx DxF F Bx -=(与假设方向相反) ∑=0B M02=⋅-⋅-a F a F Dx AxF F Ax -=(与假设方向相反)3-12AD AC AB ,,和BC 四杆连接如图所示。

在水平杆AB 上作用有铅垂向下的力F 。

接触面和各铰链均为光滑的，杆重不计，试求证不论力F 的位置如何，杆AC 总是受到大小等于F 的压力。

解：取整体为研究对象，受力如图所示，列平衡方程：∑=0C M0=⋅-⋅x F b F DF bx F D =F CF C yF DF CxF CyF BxF ByF DxF DyF HyF BxF ByF DyF DxF Ax F Ay取杆AB 为研究对象，受力如图所示，列平衡方程：∑=0A M0=⋅-⋅x F b F BF bx F B =杆AB 为二力杆，假设其受压。

取杆AB 和AD 构成的组合体为研究对象，受力如图所示，列平衡方程：∑=0E M02)2(2)(=⋅--⋅+⋅+bF x b F b F F AC D B解得F F AC =，命题得证。

注意：销钉A 和C 联接三个物体。

静力学第三章空间力系空间力系是各力的作用线不在同一平面内的力系。

这是力系中最一般的情形。

许多工程结构和机械构件都受空间力系的作用，例如车床主轴、桅式起重机、闸门等。

对它们进行静力分析时都要应用空间力系的简化和平衡理论。

本章研究空间力系的简化和平衡问题，并介绍物体重心的概念和确定重心位置的方法。

与研究平面力系相似，空间力系的简化与平衡问题也采用力系向一点简化的方法进行研究。

第一节空间力的分解与投影一、空间力的分解如图3-1所示，设力F 沿直角坐标轴的分力分别为F x、F y、F z，则(3-1)图3-1力F的三个分力可以用它在三个相应轴上的投影来表示：(3-2)则(3-3)其中i、j、k分别是x、y、z轴的正向单位矢量。

二、空间力的投影1.直接投影法如图3-2所示，若已知力F与空间直角坐标轴x、y、z正向之间夹角分别为α、β、γ，以F x、F y、Fz表示力F在x、y、z三轴上的投影，则(3-4)力在坐标轴上的投影为代数量。

在式(3-4)中，当α、β、γ为锐角时，投影为正，反之为负。

图3-22.二次投影法若力F在空间的方位用图3-3所示的形式来表示，其中γ为力F与z轴的夹角，φ为力F所在铅垂平面与x轴的夹角，则可用二次投影法计算力F在三个坐标轴上的投影。

先将力F向z轴和xy平面投影，得注意：力在平面上的投影F xy为矢量。

再将F xy向x、y轴投影，得因此(3-5)图3-3反之，若已知力在直角坐标轴上的投影，则可以确定该力的大小和方向。

(3-6)其中α、β、γ为力F分别与x、y、z轴正向的夹角。

静力学第三章空间力系第二节力对点之矩与力对轴之矩一、力对点之矩在平面问题中，力F与矩心O 在同一平面内，用代数量M O(F)就足以概括力对O 点之矩的全部要素。

但在空间问题中，由于各力与矩心O所决定的平面可能不同，这就导致各力使刚体绕同一点转动的方位也可能不同。

为了反映转动效应的方位，力对点之矩必须用矢量表示。

第三章-静力学的基本知识（二）第一节静力学的基本知识8.力偶和力偶矩力偶——大小相等的二个反向平行力称之为一个力偶。

力偶的作用效果是引起物体的转动，和力矩一样，产生转动效应。

力偶的转动效应用力偶矩表示，它等于力偶中任何一个力的大小与力偶臂d 的乘积，加上适当的正负号，即式中：F 是力的大小：d 是力偶臂，是力偶中两个力的作用线之间的距离。

逆时针为正，顺时针为负。

常用单位为KN·m 。

力偶特性一：力偶的转动效应与转动中心的位置无关，所以力偶在作用平面内可任意移动。

力偶特性二：力偶的合力为零，所以力偶的效应只能与转动效应平衡，即只能与力偶或力矩平衡，而不能与一个力平衡。

9.约束和约束反力（1）柔索：由柔软的绳索、链条或皮带构成的约束绳索类只能受拉，约束反力作用在接触点，方向沿绳索背离物体。

约束力方向与所能限制的物体运动方向相反。

（2）光滑支承面约束约束反力作用在接触点处，方向沿公法线，指向受力物体。

（3）光滑圆柱铰链约束①固定铰支座：物体与固定在地基或机架上的支座有相同直径的孔，用一圆柱形销钉联结起来，这种构造称为固定铰支座。

中间铰：如果两个有孔物体用销钉连接2个约束，1个自由度。

固定铰支座②可动铰支座在固定铰链支座的底部安装一排滚轮，可使支座沿固定支承面滚动。

1个约束，2个自由度。

③固定端支座3个约束，0个自由度。

10.物体的受力分析和受力图画受力图的方法与步骤：（1）取隔离体（研究对象）（2）画出研究对象所受的全部主动力（使物体产生运动或运动趋势的力）（3）在存在约束的地方，按约束类型逐一画出约束反力（4）取隔离体时的抛弃部分对分离体的力不能丢。

【例】画出重物和AB杆的受力图【例-2017年真题】二力平衡公理中，作用于刚体的两个力，使刚体维持平衡的充分与必要条件应满足（）。

A.大小相等、方向相同B.大小相等、方向相反C.大小不等、方向相同D.大小不等、方向相反答案：B【例-2017年真题】平面一般力系向其作用面内一点简化时，一般可得作用于该点的（）。

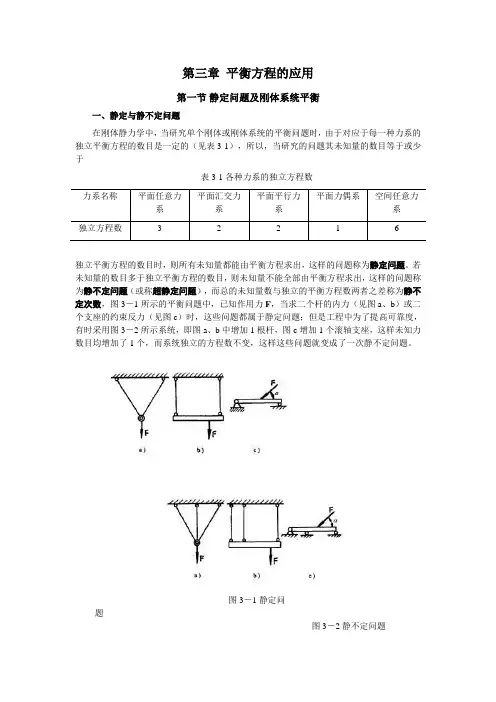
第三章平衡方程的应用第一节静定问题及刚体系统平衡一、静定与静不定问题在刚体静力学中，当研究单个刚体或刚体系统的平衡问题时，由于对应于每一种力系的独立平衡方程的数目是一定的（见表3-1），所以，当研究的问题其未知量的数目等于或少于表3-1 各种力系的独立方程数独立平衡方程的数目时，则所有未知量都能由平衡方程求出，这样的问题称为静定问题。

若未知量的数目多于独立平衡方程的数目，则未知量不能全部由平衡方程求出，这样的问题称为静不定问题（或称超静定问题），而总的未知量数与独立的平衡方程数两者之差称为静不定次数，图3－1所示的平衡问题中，已知作用力F，当求二个杆的内力（见图a、b）或二个支座的约束反力（见图c）时，这些问题都属于静定问题；但是工程中为了提高可靠度，有时采用图3－2所示系统，即图a、b中增加1根杆，图c增加1个滚轴支座，这样未知力数目均增加了1个，而系统独立的方程数不变，这样这些问题就变成了一次静不定问题。

图3－1 静定问题图3－2 静不定问题静不定问题仅用刚体静力平衡方程是不能完全解决的，需要把物体作为变形体，考虑作用于物体上的力与变形的关系（见本书第二篇），再列出补充方程来解决。

在关于静不定问题的求解，已超出了本章所研究的范围。

二、刚体系统的平衡问题由若干个物体通过约束联系所组成的系统称为物体系统，简称为物系。

本篇讨论刚体静力学，将物体视为刚体，所以物体系统也称为刚体系统。

当整个系统平衡时，则组成该系统的每一个刚体也都平衡，因此研究这类问题时，既可取系统中的某一个物体为分离体，也可以取几个物体的组合或取整个系统为分离体。

一旦取出分离体后，该分离体以外物体对于这个分离体作用的力称为外力，分离体系统内各物体间相互作用的力称为内力。

在研究刚体系统的平衡问题时，不仅要分析外界物体对于这个系统作用的力（外力），有时还需要分析系统内各物体间相互作用的力（内力）。

由于内力总是成对出现的，因此，当取整个系统为研究对象时，可不考虑其内力。