20111019数据查询(1)答案

海淀区九年级第一学期期末练习数 学参考答案及评分标准 2011.1说明： 合理答案均可酌情给分，但不得超过原题分数 一、选择题（本题共32分，每小题4分）二、填空题（本题共16分，每小题4分）注：第12题答对一个给2分，答对两个给4分 三、解答题（本题共30分，每小题5分）13.解：原式=…………………………….…………………………….2分=…………………………….…………………………….4分 =6 …………………………….…………………………….5分 14．（1）解： 48,…………………………….…………………………….1分 0.81…………………………….…………………………….2分 （2）解：()90.8P =射中环以上…………………………….…………………………….4分从频率的波动情况可以发现频率稳定在0.8附近，所以这名运动员射击一次时“射中9环以上”的概率是0.8. …………………………….…………………………….5分 注：简述的理由合理均可给分 15．解法一：因式分解，得()()620x x +-= …………………………….…………………………….2分于是得 60x +=或20x -=126,2x x =-= …………………………….…………………………….5分解法二：1,4,12a b c ===-2464b ac ∆=-= …………………………….…………………………….2分482x -±==…………………………….…………………………….4分126,2x x =-= …………………………….…………………………….5分16．解：在ABC △中，60,75B C ∠=︒∠=︒Q ,45A ∴∠=︒. …………………………….…………………………….2分AB Q 是⊙O 的直径，⊙O 与AC 交于点D, ∴290DOB A ∠=∠=︒. …………………………….…………………………….5分17．解：（1）D ；90︒. …………………………….…………………………….2分 （2）DCF DEA Q △旋转后恰好与△重合， DCF DAE ∴∆∆≌.3,2AE CF BF ∴===又. 5BC BF CF ∴=+=. AED BFDE ABFD S S S ∆∴=+四边形四边形DCF ABFD S S ∆=+四边形 ABCD S =正方形2BC =25=…………………………….…………………………….5分 18．解：设该地区2009年到2011年高效节能灯年销售量的平均增长率为x . ……………….1分依据题意，列出方程 ()210114.4x += ……………………….…………………………….2分 化简整理，得： ()21 1.44x +=,解这个方程，得 1 1.2x +=±, ∴ 120.2, 2.2x x ==-.∵ 该地区2009年到2011年高效节能灯年销售量的平均增长率不能为负数.∴ 2.2x =-舍去.∴ 0.2x =. …………………….…………………………….4分 答：该地区2009年到2011年高效节能灯年销售量的平均增长率为20%. …………….5分 四、解答题（本题共20分，每小题5分） 19．（1）解：连结OD ，OE ，OC ，∵半圆与AC ，BC 分别相切于点D ，E . ∴OD AC ⊥,且DCO ECO ∠=∠. ∵AC BC =，∴CO AB ⊥且O 是AB 的中点. ∴122AO AB ==. ∵120C ∠=︒,∴60DCO ∠=︒. ∴30A ∠=︒.∴在R t AOD △中，112OD AO ==. 即半圆的半径为1.…………………………….…………………………….3分（2）设CO =x ，则在R t AOC △中，因为30A ∠=︒，所以AC =2x ，由勾股定理得： 222AC OC AO -= 即 222(2)2x x -= 解得x =x =舍去）∴11422ABC S AB OC =⋅=⨯=△. ……….…………………………….4分∵ 半圆的半径为1， ∴ 半圆的面积为2π,∴2S π=-阴影 …………………………….…………………………….5分20．（1）解：过O 作ON CD ⊥于N ，连结OM ，则OM BC ⊥.∵ AC 是正方形ABCD 的对角线，∴ AC 是BCD ∠的平分线. ∴ OM =ON.即圆心O 到CD 的距离等于⊙O 半径，∴ CD 与⊙O 相切. …………………………….…………………………….3分 （2）由（1）易知MOC △为等腰直角三角形，OM 为半径， ∴ OM =MC =1.∴ 222112OC OM MC =+=+=, ∴OC∴1AC AO OC =+=+ 在R t ABC △中，AB =BC ,有 222AC AB BC =+ ∴ 222AB AC =∴AB =…………………………….…………………………….5分故正方形ABCD的边长为22. 21．（1）解：依题意画出树状图（或列表）如下或123123312m n…………………………….…………………………….2分（2）解：当240m n ->时，关于x 的方程20x mx n ++=有两个不相等实数根，而使得240m n ->的m ，有2组，即(3，1)和(3，2). ………….…………………………….4分则关于x 的方程20x mx n ++=有两个不相等实数根的概率是13.∴P （有两个不等实根）=13…………………….5分22．（1）证明：如图一，连结OC ，则OC EF ⊥，且OC=OA , 易得OCA OAC ∠=∠.∵ AD EF ⊥，∴OC//AD.∴OCA ∠=CAD ∠,∴CAD ∠=OAC ∠. 即 CAD BAC ∠=∠.…………………………….…………………………….2分 （2）解：与CAD ∠相等的角是BAG ∠.…………………………….…………………………….3分证明如下： 如图二，连结BG .∵ 四边形ACGB 是O e 的内接四边形， ∴ 180ABG ACG ∠+∠=︒. ∵ D ，C ，G 共线， ∴ 180ACD ACG ∠+∠=︒. ∴ ACD ABG ∠=∠. ∵ AB 是O e 的直径, ∴90BAG ABG ∠+∠=︒ ∵ AD EF ⊥∴90CAD ACD ∠+∠=︒ ∴ CAD BAG ∠=∠.…………………………….…………………………….5分五、解答题（本题共22分，第23题7分，第24题7分，第25题8图一图一23．（1）解：如图一，连结AQ ．由题意可知：OQ =OA =1. ∵OP =2,∴A 为OP 的中点.∵PQ 与O e 相切于点Q ,∴OQP △为直角三角形. …………1分∴112AQ OP OQ OA ==== . …………2分即ΔOAQ 为等边三角形. ∴∠QOP =60°． …………3分（2）解：由（1）可知点Q 运动1秒时经过的弧长所对的圆心角为30°，若Q 按照（1）中的方向和速度继续运动，那么再过5秒，则Q 点落在O e 与y 轴负半轴的交点的位置（如图二）.设直线PQ 与O e 的交点为D ，过O 作OC ⊥QD 于点C ，则C 为QD 的中点. …………4分 ∵∠QOP =90°，OQ =1，OP =2, ∴QP=. (5)∵1122OQ OP QP OC ⋅=⋅, ∴OC . …………6分∵OC ⊥QD ，OQ =1，OC ,∴QC ∴QD …………7分 24．（1）解：∵关于x 的方程为221(1)04x a -++=为一元二次方程，且有实根.故满足：220,1(4(1)0.4a a ≥⎧⎪⎨∆=--⨯⨯+≥⎪⎩ ……….…………………………….2分（注：每个条件1分） 整理得 20,(1)0.a a ≥⎧⎨-≤⎩∴1a =……….…………………………….4分（2）由（1）可知1a =,故（2）中的方程2(1)0mx m x a +--=可化为2(1)10mx m x +--=.①当m =0时，原方程为10x -=，根为1x =，符合题意.………………………….5分图二②当m ≠0时，2(1)10mx m x +--=为关于x 的一元二次方程，Δ=2222(1)4(1)12421(1)0m m m m m m m m --⨯⨯-=-++=++=+≥.此时，方程的两根为 1211,x x m==-. ∵两根均为整数, ∴m =1±.………………………….7分综上所述，m 的值为1-，0 或1.25．（1）证明：如图一，∵1O ，2O ，F 分别是AB ，AC ，BC 边的中点，∴1O F ∥AC 且1O F =A 2O ，2O F ∥AB 且2O F =A 1O ， ∴∠B 1O F=∠BAC ，∠C 2O F=∠BAC , ∴∠B 1O F=∠C 2O F∵点D 和点E 分别为两个半圆圆弧的中点， ∴1O F =A 2O =2O E ，2O F =A 1O =1O D ， ………………………….2分∠B 1O D =90°，∠C 2O E =90°， ∴∠B 1O D=∠C 2O E . ∴∠D 1O F=∠F 2O E .∴12DO F FO E △≌△. ………………………….3分（2）解：如图二，延长CA 至G ，使AG =AQ ,连接BG 、AE .∵点E 是半圆2O 圆弧的中点， ∴AE=CE=3∵AC 为直径 ∴∠AEC =90°，∴∠ACE =∠EAC =45°，AC∵AQ 是半圆2O 的切线，∴CA ⊥AQ ，∴∠CAQ =90°， ∴∠ACE =∠AQE =45°，∠GAQ =90° ∴AQ =AC =AG=图一图二同理：∠BAP =90°，AB =AP=∴CG=∠GAB =∠QAP ∴AQP AGB △≌△.……………………..5分∴PQ =BG ∵∠ACB =90°，∴BC∴BG∴PQ=……………………..6分（3） 证法一：如图三，设直线F A 与PQ 的垂足为M ，过C 作CS ⊥MF 于S ，过B 作BR ⊥MF 于R ，连接DR 、AD 、DM.∵F 是BC 边的中点，∴ABF ACF S S =△△. ∴BR=CS ，由（2）已证∠CAQ =90°, AC =AQ, ∴∠2+∠3=90°∵FM ⊥PQ , ∴∠2+∠1=90°， ∴∠1=∠3, 同理：∠2=∠4,∴AMQ CSA △≌△，∴AM=CS ， ∴AM=BR ，同（2）可证AD=BD ，∠ADB =∠ADP =90°,∴∠ADB =∠ARB =90°, ∠ADP =∠AMP =90°∴A 、D 、B 、R 四点在以AB 为直径的圆上，A 、D 、P 、M 四点在以AP 为直径的圆上， 且∠DBR+∠DAR =180°,∴∠5=∠8, ∠6=∠7, ∵∠DAM +∠DAR =180°, ∴∠DBR =∠DAM ∴DBR DAM △≌△， ∴∠5=∠9, ∴∠RDM =90°， ∴∠5+∠7=90°， ∴∠6+∠8=90°， ∴∠P AB =90°，∴P A ⊥AB ,又AB 是半圆1O 直径， ∴P A 是半圆1O 的切线.……………………..8分证法二：假设P A 不是是半圆1O 的切线，如图四，过点A 作半圆1O 的切线交BD 的延长线于点P '，图三则点P '异于点P ，连结P Q '，设直线F A 与PQ 的 垂足为M ，直线F A 与P Q '的交点为M '.延长AF 至N ，使得AF =FN ，连结BN ，CN ，由于点F 是 BC 中点，所以四边形ABNC 是平行四边形. 易知，180BAC ACN ∠+∠=︒， ∵AQ 是半圆2O 的切线,∴∠QAC =90°，同理90P AB '∠=︒. ∴180P AQ BAC '∠+∠=︒. ∴P AQ ACN '∠=∠.由（2）可知，,AQ AC AB AP '==,∴P AQ NCA '△≌△. ∴NAC P QA '∠=∠. ∵90QAC ∠=︒,∴90NAC M AQ '∠+∠=︒. 即 90AQM M AQ ''∠+∠=︒.∴90AM Q '∠=︒. 即 P Q AF '⊥.∵ PQ AF ⊥,∴ 过点Q 有两条不同的直线P Q '和PQ 同时与AF 垂直.这与在平面内过一点有且仅有一条直线与已知直线垂直相矛盾,因此假设错误.所以P A 是是半圆1O 的切线.Q图四。

2011年数学建模B题参考答案摘要本论文主要研究合理设置与调度交巡警服务平台问题。

通过合理设置交巡警服务平台的位置、分配其管辖范围以及合理调度，使各交巡警服务平台最大程度的发挥其职能。

针对问题一：（1）对交巡警服务平台划分管辖区域实际上是利用最短路算法解决平台到其他任意节点的最短路问题。

考虑在以及警务资源有限两个条件，合理为交巡警服务平台分配管辖区域。

通过C++编程和WINQSB软件，用Dijkstra算法计算出任意两节点之间的最短路，将A区节点划分为20个区域，从而得到各个交巡警服务平台的管辖范围。

（见表2）(2)此问题是20个警务平台警力派往13个要道路口的最优分配问题，建立0-1规划模型，得到A区交巡警服务平台对十三条交通要道的快速全封锁的解决方案。

即在最短的时间内，可以全部封锁十三条交通要道。

假设一个交巡警服务平台可以封锁一个路口，将问题简化，转化为n-n的分配问题。

(3)交巡警服务平台工作量和出警时间可以由平台辖区内发案率作为标准，对问题进行定性与定量分析，运用分阶段决策思想利用Excel求出并比较添加交巡警服务平台前后发案率的方差得出分别在节点90、69、31处增加交巡警服务平台。

针对问题二：（4）交巡警平台设置合理与否，与各城区人口比例、各城区重要交通要道个数、各城区发案率都和其自己城区交巡警平台个数有着直接关系。

考虑一个市交警平台设置方案的合理性，可以以城区为单位，进行比较判断。

为了方便计算分析，定义了交巡警平台设置系数，于是建立了城区合理性判断模型：城区人口、城区要道个数、城区发案率总和以及交警平台设置系数的乘积为各城区交巡警平台个数，得出结果B、C城区交巡警设置不合理，分析原因后，对平台位置进行重新分配，对方案进行了优化。

（5）本题是求围堵犯罪嫌疑人的最优化问题，通过定性与定量分析，可用十二个节点10、14、560、561、581、177、202、203、317、264、248、251围堵将犯罪嫌疑人堵截在A、C两区。

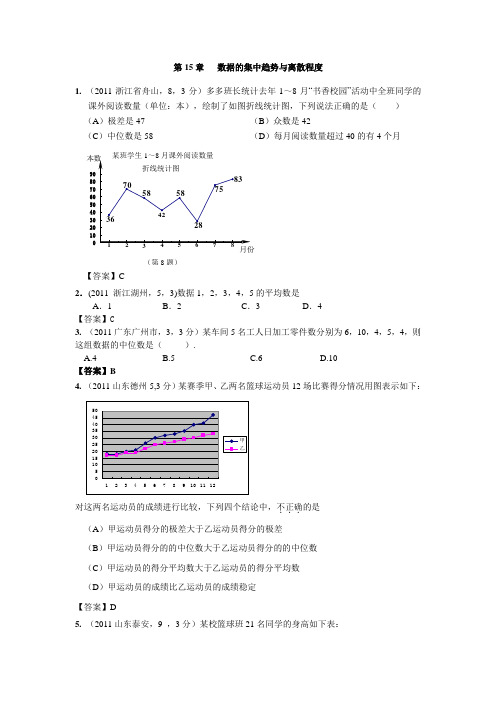
第15章 数据的集中趋势与离散程度1. （2011浙江省舟山，8，3分）多多班长统计去年1～8月“书香校园”活动中全班同学的课外阅读数量（单位：本），绘制了如图折线统计图，下列说法正确的是（ ） （A ）极差是47（B ）众数是42（C ）中位数是58（D ）每月阅读数量超过40的有4个月【答案】C2．(2011 浙江湖州，5，3)数据1，2，3，4，5的平均数是A ．1B ．2C ．3D ．4 【答案】C3. （2011广东广州市，3，3分）某车间5名工人日加工零件数分别为6，10，4，5，4，则这组数据的中位数是（ ）. A.4B.5C.6D.10【答案】B4. （2011山东德州5,3分）某赛季甲、乙两名篮球运动员12场比赛得分情况用图表示如下：5101520253035404550123456789101112甲乙对这两名运动员的成绩进行比较，下列四个结论中，不正确．．．的是 （A ）甲运动员得分的极差大于乙运动员得分的极差 （B ）甲运动员得分的的中位数大于乙运动员得分的的中位数 （C ）甲运动员的得分平均数大于乙运动员的得分平均数 （D ）甲运动员的成绩比乙运动员的成绩稳定 【答案】D5. （2011山东泰安，9 ，3分）某校篮球班21名同学的身高如下表：10203040506070809012345678某班学生1～8月课外阅读数量折线统计图3670585842287583本数月份（第8题）12345678身高（cm ） 180 186 188 192 208 人数（个）46542则该校篮球班21名同学身高的众数和中位数分别是（单位：cm ）（ ）A.186,186B.186,187C.186,188D.208,188【答案】C6. （2011山东威海，2，3分）今年体育学业考试增加了跳绳测试项目，下面是测试时记录员记录的一组（10名）同学的测试成绩（单位：个/分钟）． 176 180 184 180 170 176 172 164 186 180该组数据的众数、中位数、平均数分别为（ ）A ．180， 180， 178B ．180， 178， 178C ．180， 178， 176.8D ．178， 180， 176.8【答案】C7. （2011山东烟台，8,4分）体育课上测量立定跳远，其中一组六个人的成绩（单位：米）分别是：1.0,1.3,2.2,2.0,1.8,1.6 ,则这组数据的中位数和极差分别是（ ）A.2.1,0.6B. 1.6,1.2C.1.8,1.2D.1.7,1.2 【答案】D8. （2011四川南充市，2，3分）学校商店在一段时间内销售了四种饮料共100瓶，各种饮料的销售量如下表：品牌 甲 乙 丙 丁 销售量（瓶）12321343建议学校商店进货数量最多的品牌是（ ）（A ）甲品牌 （B ）乙品牌 （C ）丙品牌 （D ）丁品牌 【答案】D9. （2011广东湛江9,3分）甲、乙、丙、丁四人进行射箭测试，每人10次射箭成绩的平均数都是8.9环，方差分别是20.65S =甲，20.55S =乙，20.50S =丙20.45S =丁，则射箭成绩最稳定的是A 甲B 乙C 丙D 丁 【答案】D10. （2011贵州安顺，4，3分）我市某一周的最高气温统计如下表：最高气温（℃）25 26 27 28 天 数1123则这组数据的中位数与众数分别是（ ） A ．27，28 B ．27.5，28 C ．28，27 D ．26.5，27 【答案】A11. （2011浙江衢州，1,3分）在九年级体育中考中，某校某班参加仰卧起坐测试的一组女生（每组8人）测试成绩如下（单位：次/分）：44,45,42,48,46,47,45.则这组数据的极差为（ ） A.2 B.4 C.6 D.8 【答案】C12. （2011浙江省，4，3分）某校七年级有13名同学参加百米竞赛，预赛成绩各不相同，要取前6名参加决赛，小梅已经知道了自己的成绩，她想知道自己能否进入决赛，还需要知道这13名同学成绩的（ ）A .中位数B .众数C .平均数D . 极差 【答案】A13. （2011浙江台州，3,4分）要反映台州某一周每天的最高气温的变化趋势，宜采用（ ）A . 条形统计图B . 扇形统计图C . 折线统计图D .频数分布直方图【答案】C14. （2011浙江温州，2，4分）某校开展形式多样的“阳光体育”活动，七(3)班同学积极响应，全班参与，晶晶绘制了该班同学参加体育项目情况的扇形统计图（如图所示），由图可知参加人数最多的体育项目是()A ．排球B ．乒乓球C ．篮球D ．跳绳 【答案】C16. （2011浙江省嘉兴，8，4分）多多班长统计去年1～8月“书香校园”活动中全班同学的课外阅读数量（单位：本），绘制了如图折线统计图，下列说法正确的是（ ） （A ）极差是47（B ）众数是42（C ）中位数是58（D ）每月阅读数量超过40的有4个月【答案】C18. （2011台湾台北，14）图(四)为某班甲、乙两组模拟考成绩的盒状图。

1.A.【解析】由第一幅图表中读数发现：2011年我国外出农民工月均收入水平最高的地区是直辖市，而与2010年相比，各地区收入增幅相差不多，即2010年收入水平最高地区的仍为直辖市。

因此，本题答案选择A选项。

2.B.【解析】由“2011年，全国外出农民工月均收入2049元，同比增长21.2%，比去年同期提高了1.2个百分点。

”可得2010年，我国外出农民工月均收入约为20491700 121.2%-=+，增长率为21.2%-1.2%=20%，故09年收入约为17001400120%-≈+元。

因此，本题答案选择B选项。

3.C.【解析】首先由材料可判断出自营人员月均收入高于受雇人员，故排除A、D两项；又因为669元为2011年自营人员与受雇人员的收入差值，2010年的差值小于669元，故排除B项。

因此，本题答案选择C选项。

4.C.【解析】忽略权重的话只需将这六个行业的数据直接加和再除以6即可。

即（1920+2382+2485+2024+1807+1826）=2074元。

因此，本题答案选择C选项。

5.D.【解析】本题为综合分析类题目。

A项，由第3题可以推出，故A项正确；B项，增幅即增长率，由材料中第一段可直接读数比较，故B项正确；C项，由图一中可以看出，总体上看大城市的农民工月均收入高于小城市，故C项正确；D项，虽然在建制镇务工的外出农民工与从事住宿和餐饮业的外出农民工平均收入分别为表中最低，但是二者之间没有必然联系，不能推出在建制镇从事住宿和餐饮业的外出农民工的月均收入最低，故D项错误。

因此，本题答案选择D选项。

6.A.【解析】本题考查基期量计算。

由表中数据，2011年9月，社会消费品零售总额绝对量为18227114.2%+，采用直除法，直除三位得159。

因此，本题答案选择A选项。

（14.2%≈17，同样可近似计算。

）7.D.【解析】本题考查直接读数。

由表中最后一栏1~9月同比增速读数得：通讯器材同比增速33.3%为最高。

抽样技术课后习题-参考答案-金勇进第二章习题2.1判断下列抽样方法是否是等概的：（1）总体编号1~64，在0~99中产生随机数r ，若r=0或r>64则舍弃重抽。

（2）总体编号1~64，在0~99中产生随机数r ，r 处以64的余数作为抽中的数，若余数为0则抽中64.（3）总体20000~21000，从1~1000中产生随机数r 。

然后用r+19999作为被抽选的数。

解析：等概抽样属于概率抽样，概率抽样具有一些几个特点：第一，按照一定的概率以随机原则抽取样本。

第二，每个单元被抽中的概率是已知的，或者是可以计算的。

第三，当用样本对总体目标进行估计时，要考虑到该样本被抽中的概率。

因此（1）中只有1~64是可能被抽中的，故不是等概的。

（2）不是等概的【原因】（3）是等概的。

2.2抽样理论和数理统计中关于样本均值y 的定义和性质有哪些不同？2.3为了合理调配电力资源，某市欲了解50000户居民的日用电量，从中简单随机抽取了300户进行，现得到其日用电平均值=y 9.5（千瓦时），=2s 206.试估计该市居民用电量的95%置信区间。

如果希望相对误差限不超过10%，则样本量至少应为多少？解：由已知可得，N=50000，n=300，5.9y =，2062=s1706366666206*300500003001500001)()ˆ(222=-=-==s nf N y N v YV 19.413081706366666(==）y v 该市居民用电量的95%置信区间为[])(y [2y V z N α±=[475000±1.96*41308.19]即为（394035.95，555964.05） 由相对误差公式y)(v u 2y α≤10%可得%10*5.9206*n50000n 1*96.1≤- 即n ≥862欲使相对误差限不超过10%，则样本量至少应为8622.4某大学10000名本科生，现欲估计爱暑假期间参加了各类英语培训的学生所占的比例。

每日一练之资料分析阅读以下资料，回答问题。

2011年我国网上购物保持高速发展态势，全年网购总额达到8090亿元，比2010年增长72.90%，占到了全国社会商品零售总额的4.46%；网购人数达到2.12亿，比2010年增长14.59%，占到2011年全部网民数的41.50%，比2010年提高了0.9个百分点。

某调查机构选取4大区域中最具代表性的30个城市为目标调查地，调查数据显示，2011年这30个城市共有8626万个网购消费者,网购总额占到当年全国网购总额的44.67%，服装是网上购买人数和购买金额均最多的商品类别。

2011年中国服装网购市场总额为全年网购总额的33.00%，年增长率高于总体网购市场增长率20.60个百分点。

2011年4大区域中购物网站的市场份额（%）1.2011年中国服装网购总额年增长率为（）。

A.14.59%B.41.5%C.72.9%D.93.5%解析D。

11年总体网购增长率72.9%，服装年增长率高于其20.6个百分点，可知服装增长率是93.5%。

2.2010年我国人均网购金额约为（）。

A.2000元B.2500元C.3800元D.4200元解析3.2011年上述表格所列购物网站中，有2个以上区域市场比其抽样市场平均份额高10个百分点的是（）。

A.A网站B.B网站C.C网站D.D网站解析A。

由于真题试卷印刷错误，题干存在问题，表格中的数据无法体现“高10个百分点”，本题无正确答案，ABCD四个选项都得分。

4.从上述资料不能推出的是（）。

A.2011年全国网民人数B.2010年中国服装网购市场总额C.2011年四大区域以外网民的人均网购金额D.2010年A网站在30个目标城市中所占的市场份额解析D。

A选项可由网购人数和其占网民数比例得到；B选项11年网购市场总额已知，比10增长率是多少已知，所以10年市场总额可得；C选项同样可由材料信息得出；D选项只知道2011年的A网站在30个目标城市中所占的市场份额，不知道相对于2010年的变化情况，无从求出2010年相应的市场份额。