卷积积分图解法

t
e RC
RCT
T RC t
e RCT 0
RC T RC
(t 0)
u0T T RC
e
t T
t
e RC
ε(t)
➢卷积积分的图解
求f(t)与h(t)的卷积，实质上是求一个新函数
f()h(t)在 由0到t的区间内的定积分。根据定积分的 几何意义，函数在0到t区间内的定积分值，决定于被积 函数f()h(t)的曲线在该区间内与 轴之间所限定的面
§4-6 卷积积分及零状态响 应的卷积计算法
➢ 卷积积分的推导
激励函数的 近似表示
f (t) fa (t) f (0)ε(t) ε(t )
f ( )ε(t ) ε(t 2 )
f (2 )ε(t 2 ) ε(t 3 )
f (n 1) ε(t (n 1) ) ε(t n )
解： [e tε(t)] ε(t) t e ε( )ε(t )d 0
t ed 0
1 e t
0
(t 0)
(t 0)
1 1 e t ε(t)
例2 设图示RC串联电路中电压源的电压
t
u(t) u0e T ε(t)
求零状态响应电压uC(t)。
解： 用卷积积分公式求uC(t)，应先求冲激响应
如按
t
r(t) h( ) f (t ) d h(t) f (t)
0
当 0<t <1 时
计算。
r(t ) te ε( )d t e d 1 et
0
0
当 t >1时
r(t ) t e ε( )d t 1
t e d e(t1) et t 1 返回
注意ቤተ መጻሕፍቲ ባይዱ分上、下限

f
(i 2
j
)
(t
)
f (t)
f1(1) (t)
f (1) 2
(t
)
d dt
f1(t)
t
f2 ()d
常数信号(直流信号) f (t) E ( t ) 经微分后为零,需特殊考虑, 不能用微分性质
15
三、与冲激函数或阶跃函数的卷积
f (t) (t) f (t)
f (t) (t) ( ) f (t )d f (t)
1 1
2
1
1 2
(t
)d
3t 3 4 16
7
r(t) e(t) h(t) e( )h(t )d
h(t )
e( )
t
(3) 1 t 3 2
e(t) h(t) 3 t 3 4 16
(4) 3 t 3
e( )
2
h(t )
t
e(t) h(t) 1 1 1 (t )d
t2
4
t 4
1 16
( 1 t 1) 2
r(t) e(t) h(t)
r(t)
43
t
3 16
(1 t 3) 2
t2
t
3
( 3 t 3)
4 2 4 2
0
其它
t
卷积结果所占的时宽等于两个函数各自时宽的总和
10
P842 14(1) f (t) u(t) u(t 1),求s(t) f (t) f (t)
(1) t 0时, s(t) 0
(2)
0 t 1时,
s(t)
t
d t
0
(3)
1 t 2时,
s(t)
1

(1) n<0
x(m) m 0 4 h(n-m) m n-6 n0
y(n) = x(n) ∗ h(n) = 0
x(m) m
(2)在0≤n≤4区间上
0
4 h(n-m) m
n-6 0 n 4
∴ y(n) = ∑ x(m)h(n − m) = ∑1⋅ a
m=0 n m=0
n
n
n−m
=a
n
m=0
∑a
−m
1− a =a −1 1− a
n
−( n+1)
1− a =1− a
1+n
x(m)
(3)在4<n≤6区间上
m 0 4 h(n-m) m n-6 0
1+n
∴ y(n) = ∑x(m)h(n − m)
m=0
4
= ∑1⋅ a
m=0 n
4
n−m
=a
n
m=0
∑a
n−4
4
−m
4 6 n
1− a a −a =a = −1 1− a 1− a
−(1+4)
x(m) m 0 4 h(n-m) m 0 n-6
7
(4)在6<n≤10区间上
∴ y(n) = =
m=n−6
∑x(m)h(n − m)
=a
n m=n−6 −( 4+1)
n
m=n−6
∑1⋅ a
n
n
n−m
∑a
=
4
−m
6
n
10
=a
a
−( n−6)
−a −1 1− a
a
n−4
−a 1− a
综合以上结果， 可归纳如下： 综合以上结果，y(n)可归纳如下： 可归纳如下

3
7) t≥7时,
y(t ) 0
注意：积分上下限应由被 积函数存在的时域范围的 上下限确定。
卷积积分在电路分析中的应用
例1、电路如图所示，uS=15e-0.25t(t)V。采用卷积计算uC。
解：以uC为响应，求单位阶跃响应
uC (0 ) uC (0 ) 0
uCf 40 1 0.5V 40 40
t t
t t
t 0
d dt t t
卷积积分上下限分析
t
0
r t h t f t f t h t
卷积符合交换律
δ t f t δ f t dτ τ τ
k 0
f (t ) f a (t )
f ( k ) ( t k ) ( t ( k 1) )
k 0 n 1

k 0 n 1
k 0
n 1
(t k ) (t (k 1) ) f (k )
例2、电路如图，R=10，L=1H，激励uS的波形如图 所示，求零状态响应i(t)。
解：以电流i 为响应，求单位阶跃响应为：
R t 1 g( t ) (1 e L ) ( t ) R 0.1(1 e 10 t ) ( t )
则单位冲激响应为：
dg( t ) h (t ) e 10 t ( t ) dt
40 40 RC 0.05 1s 40 40
uC ( t ) uCf (1 e ) ( t ) 0.5(1 e t ) ( t )V
t
单位阶跃响应为：
g(t ) 0.5(1 e t ) (t )

− 2t
= 6∫ e
0
t
− 2τ
dτ ε (t ) = 3(1 − e
) ε (t )
f1 (t ) ∗ f 3 (t ) = =
∫
∞
−∞
f1 (τ ) f 3 (t − τ )dτ
∫
∞
−∞
3e ε (τ ) ⋅ 2ε (t − τ − 2)dτ
− 2τ
=6
∫
t −2
e
− 2τ
0
dτ = 3(1 − e
问：
y2 (t ) = [ f (t − t1 )ε (t − t1 )]∗ [h(t − t 2 )ε (t − t 2 )]
y1 (t ) = [ f (t − t0 )ε (t − t0 )]∗ [h(t )ε (t )]
2）反因果信号 ）
=
t
y (t ) = [ f (t )ε (− t )]∗ [h(t )ε (t )]
∫
（1）翻转 ） （2）平移 ） （3）相乘 ） （4）积分 ）
f1 (τ ) → f1 (−τ )或 : f2 (τ ) → f2 (−τ )
f1(−τ ) → f1(t −τ )或f2 (−τ ) → f2 (t −τ )
f1 ( t − τ ) f 2 (τ )或f 2 ( t − τ ) f1 (τ )
(1)
＝
－1 0
1 t o t0 t o t 0－1 t 0 t 0＋1 t
图 2.2 – 3 例2.2 - 3图 图
例2.4-3 周期性单位冲激序列
δ T (t ) =
试求
f (t ) = f0 (t ) ∗ δ T (t )
∞ m = −∞
m = −∞

' t
dg ( t ) r ( t ) e ( t ) h ( t ) e ( t ) dt
de (t) *g(t) dt
e ( t ) e ( t ) u ( t )
de ( t ) d ( e ( t ) u ( t ))de ( t ) u ( t ) e ( t ) ( t ) dt dt dt
方法一:

h (t )
t
e( )
0


*
0
h(t ) 非零值下限是－ 卷积分下限是零 u( ) 非零值下限是 0
h(t ) 非零值上限是 t 卷积分上限是 t u( ) 非零值上限是
若两个函数的左边界分别为tl1,tl2,右边界分别为 tr1,tr2,积分的 下限为max[tl1,tl2];积分的上限为min[tr1,tr2].


f f ( ) f ( t ) d 1 2 1 2 f
0 t-2 1
t
3 . if 1 t 2
1
b ab 2 ab 2 t a ( t ) d ( t ) 0 t 0 2 4 4
t
a t-2 0 t 1
ab (2 t 1 ) 4
2.各分段内卷积积分限的确定 。
分解成单位阶跃分量之和
f (t1 )
f( t t ) 1 1 f ( 0)
t1
t1
u ( t ) g ( t ) DaHarma ln tegr
*.Duharmal integral
r(t) e(0 )g(t) e ( )g(t )d 0
1
b ab 2 1 f f a ( t ) d ( t ) 1 2 0 02 4

3.相乘：f1( ) f2 (t )
4.乘积的积分：
f1(
).
f2(t
)d
课堂练习
f1(t)=(t-1)2, f2(t)=δ(t-4),请分别用公式 法及作图法计算: y (t) = f1(t)* f2(t)
卷积计算小结
由于信号存在时间的局限性，卷积积分中积 分限的确定非常关键。
函数式复杂时，用图形分段求出积分限方便准确。
f1( )
f2
(t
)d
为f1(t)与f2(t)的卷积，记为f(t)= f1(t)*f2(t)
yzs(t)
f ( )h(t ) d f (t) * h(t)
二、卷积的计算
f
t
f1
f 2 t
d
1. f1(t) f1( ),
2. f2 (t) f2 ( ) 倒置 f2 ( ) 时延t f2 (t )
§2.3 卷积积分
• 卷积积分
• 卷积的图解法
Yun Liu, Information College, Zhongkai University of Agriculture and Engineering
一、卷积积分
1.信号的时域分解
任意信号f(t)可表示为f源自tftd
2 .任意信号作用下的零状态响应
积分
f (t) LTI系统 yzs(t)
本质
零状态
δ(t) 由时不变性： δ(t -τ)
由齐次性： f (τ)δ(t -τ)
由叠加性：
f
( ) (t
) d
‖
f (t)
h(t) h(t -τ)
f (τ) h(t -τ)
f
( )h(t ) d

§2.5 卷积积分的运算和图解
y(t) x(t) h(t) x( )h(t )d
1）将x(t)和h(t)中的自变量由t改为，成为函数的自 变量； 2）把其中一个信号翻转、平移；
h( ) 翻转h( ) 平移th(( t)) h(t )
3）将x() 与h(t )相乘；对乘积后的图形积分。
例11：画出下列系统的模拟图
y(t) 5 y(t) 3 y(t) 3x(t) x(t)
例：引入辅助函数q(t)
q(t) 5q(t) 3q(t) x(t) 利用微分特性法 y(t) 3q(t) q(t)
q(t) x(t) 5q(t) 3q(t)
例12：根据系统的模拟图写出其微分方程模型
et
d
r t
d
et
rt
et
rt
et
T rt
rt de(t)
dt
t
r(t) e(t)dt
rt et rt et T
例10：试用系统模拟图来表示下列方程所描述的LTI系统
a2 y(t) a1 y(t) a0 y(t) b2 x(t) b1 x(t) b0 x(t) a2 y(t) b2 x(t) b1 x(t) b0 x(t) a1 y(t) a0 y(t)
y(t )
1 a2
[b2 x(t )
b1 x(t )
b0 x(t )
a1
y(t)
a0
y(t )]
y(t )
1 a2
[b2 x(t )
b1 x(1) (t )
b0 x(2) (t ) a1 y(1) (t ) a0 y(2) (t )]
根据该式，可直接画出系统模拟图
y(t)

f2t
2
f
t
t2
2
3 4
d
3 4
3 2
4
t
t-2 0 t
当 t 4 时， ft0
f2t
3
4
0 t-2 t .
f (t) f1(t) f2(t)
0,
3
(t
2 ),
2
3
,
3
(4
t ),
2
0 ,
t 2 -2 t 0 0 t 2 2 t 4 t4
.
例 2.3例32： 设 f1(t)3e2t(t)， f2(t)2(t)，
f3(t)2(t2).
求 求卷积卷 积1） 积 f1(t) 分 f2(t（ )；2） （ f1(t)f3(t)。
解法一：图示法（1）
当 t 0 时 f 1 t f ， 2 t 0
f1
3
当t 0时，f1t f2t
t 3e2 2d
0
6 t e2d 3e2 t
0
0
31e2t
f 1 t f 2 t 3 1 e 2 t t .
显然上式适用于 t 2 的区间。
f 1 t * f 3 t 3 1 e 2 t 2 t 2
.
练习：画出下列图形的卷积积分
f1t
f2t
2
1
2 -1 0 t
01 2
t
. 16
f1t
2
练习题答案：f1tf2t 2 -1 0 t
2
f2t
1
-1 0 1 t
01 2 t
思考：两个时限信号的卷积积分结果有何特点？ 从非零区间长度及形状考虑。
本节小结1卷积积分的解析法2卷积积分的图解法23卷积积分卷积方法在本书中占有重要地位这里要讨论的卷积积分是将输入信号分解为众多冲激函数之和积分利用冲激响应求解lti系统对任意激励的零状态响应

卷积积分的图解计算
计算 f (t) = f1(t) ∗ f2 (t) = ∫−∞ f1(τ ) f2 (t −τ )dτ
( ff1τt)) 1(
() ff22(τt)
1 1 2 2
步骤
∞
将f2 (τ )反 得f2 (− ) 折 τ
f2 (−τ)
1 2
1 1
0 0
1 1
t
f1(τ )
0 τ 0
1 1
2 2
1Байду номын сангаас
0
1 +t −3
−1+ t
τ
−1+ t
f2 (t −τ )
1 2
0
τ
平移
第二章第1讲
1
例
1
计算 f (t) = f1(t) ∗ f2 (t) = ∫−∞ f1(τ ) f2 (t −τ )dτ
当 −1+ t < 0 即 t < 1 时： f 2 (t −τ ) 和 f1 (τ ) 没有公共的重叠部分， 1 2 故卷积 f (t) = f1 (t) ∗ f2 (t) = 0 t 0 1 2 3
1 1 1× dτ = (4 − t) −3+t 2 2
1
即为重叠部分的面积。 当 −3+t ≥1 即 t ≥ 4 时： f 2 (t −τ ) 和 f1 (τ ) 没有公共的重叠部分， 故卷积 f (t) = f1 (t) ∗ f2 (t) = 0
第二章第1讲 3
f 2 (t −τ ) f1(τ)
4
f (t)
∞
f 2 (t −τ ) f1(τ)
1
−3 + t −1+ t 0
1

b
* 0 -1 1 1 b f1 a[u(t ) u(t 1)]t t f 2 (t 1)[u (t 1) u (t 1)] j 2 2 2 f 2 f1 f 2 ( ) f1 (t ) du (t ti t j )
i 1 j 1 ti
p q i 1 i
j 1

i 1 j 1
f (t )h (t )[u( t )u(t t
j i
j
)]d
由以上讨论可知:
得出卷积积分的上下限和定义域如下:
f h

i 1 j 1
p
q
t t j
f i ( ) h j (t ) du (t t i t j )


u ( 1)u (t 2)d u ( 1)u (t 3)d
t 2


d d (t 2 1) (t 3 1) 1
1
t 2
t 3
1

du (t 2 1) du (t 3 1)
e ( ) g (t )d
'
t
0

预习§2.7 作业 p85 2-19
(a),(b),(f)
1 1
t 3
(t 3)u (t 3) (t 4)u (t 4)
*. *.快速定限表 若参与卷积的两个函数fs(t)和fl(t)都是只有一个定义段,它 们的时限长度分别为TS和TL,并且TS< TL,长函数fl(t)的左 右时限分别为LL和RL,而短函数fs(t)的的左右时限分别为LS 和RS,并规定积分号内括号统一只表示 f s ( ) f l (t ) 即只反 转时限长的函数. rs

y(t) 1 f1(τ ) f2( t - ) τ y(3)
0 (e) t >3
3
t
τ
0 (f )
3
t
例2 求下图所示函数 f1(t )和 f2 (t )的卷积积 分.
2
f1 (t ) f 2 (t )
3 4
2
0 2
2
f1 (τ )
t
0
2
f 2 ( τ )
3 4
t
解(1) )
2
0
2
τ -2
0
τ
(2) )
由前面分析知: 由前面分析知:
y zs (t ) = ∫ f (τ )h(t τ )dτ
0
tHale Waihona Puke = f (t ) h(t )
这是求解零状态响 应的另一种方法. 应的另一种方法
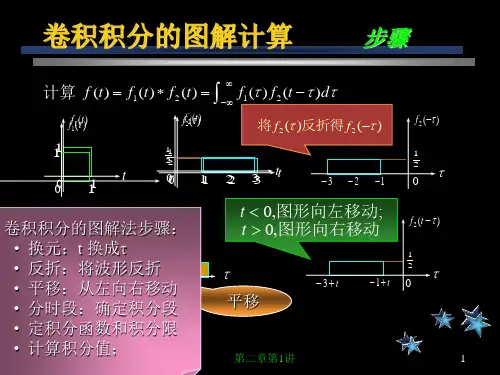
二,卷积的图示法
第一步, 波形,将波形图中的t轴 第一步,画出 f 1 ( t ) 与 f 2 ( t ) 波形,将波形图中的 轴 ) 改换成τ轴 的波形. 改换成 轴,分别得到 f1 ( τ) f 2 ( τ的波形. 和 第二步, 波形以纵轴为中心轴翻转180° 第二步,将 f 2 (τ)波形以纵轴为中心轴翻转180°, 波形. 得到 f 2 ( τ)波形. 第三步,给定一个t值 波形沿τ轴平移 轴平移|t|. 第三步,给定一个 值,将 f 2 ( τ) 波形沿 轴平移 . 在t<0时, 波形往左移;在t>0时,波形 时 波形往左移; 时 往右移. 的波形. 往右移.这样就得到了 f 2 ( t τ) 的波形.
2
2
-1
0
t
f2 (t )
1
-1
0
1

t2 2 1 t2 1 t 3
4 24
8
r(t) e(t) h(t) e( )h(t )d
e( )
h(t )
t
(4) 3 t 3 2
e(t) h(t) 1 t 2 1 t 3 4 24
(5) 3 t e(t) h(t) 0
9
r(t) e(t) h(t) e( )h(t )d
[
f1
(t
)
f2 (t)]
f1
(t
)
d dt
f2 (t)
Hale Waihona Puke d dtf1(t)
f2 (t)
t
t
[ f1() f2 ()]d f1(t) f2 ()d
t
f2 (t) f1()d
14
卷积旳微分和积分性质旳推论
f (t) f1(t) f2 (t)
f (i) (t)
f1( j) (t)
y(t) y(t) (t) y(t t0 ) y(t) (t t0 ) f1(t) f2 (t) (t t0 )
f1(t) f2 (t t0 ) f1(t t0 ) f2 (t)
20
P84 2 14(1) f (t) u(t) u(t 1),求s1(t) f (t) f (t)
f1 f2 t d
3
1
2
r(t) e(t) h(t) e( )h(t )d
e(t)或e( )
h(t)或h( )
1
2
t或
t或
h( )
h(t )
1 t
2
t
4
r(t) e(t) h(t) e( )h(t )d
e(t)或e( )
(1) t 1 2

计算卷积时一般要分几个区间分别加以考虑下面举例说明
卷积计算——图解法
y(n) x(m)h(n m) x(n) h(n)
m
计算步骤如下：
(1)翻褶：先在坐标轴m上画出x(m)和h(m)，
将hቤተ መጻሕፍቲ ባይዱm)以纵坐标为对称轴折叠成 h(-m)。
(2)移位：将h(-m)移位n，得h(n-m)。当n为
正数时，右移n；当n为负数时，左移n。
0,
n0
1 a1n , 1a
0n4
y(n)
an4 a1n
1 a
,
4n6
an4 a7
1 a
,
6 n 10
2021/3/11
0,
10 n 8
2021/3/11
m
3
(1) n<0
x(m)
m
y(n) x(n) h(n) 0
04
h(n-m)
m n-6 n 0
2021/3/11
4
x(m)
(2)在0≤n≤4区间上
m 04
h(n-m)
m
n-6 0 n 4
n
n
y(n) x(m)h(n m) 1 anm
m0
m0
n
an am
m0
an
0,
其它
a为常数，且1<a，试求x(n)和h(n)的卷积。
2021/3/11
2
解 参看图，分段考虑如下：
x(m)
n 04
h(m)
n 06
h(n-m)
(1)对于n<0；
n-6 n
(2)对于0≤n≤4；
(3)对于n>4，且n-6≤0，即4<n≤6；

如按式
t
r(t)
f (t) h(t) 0
f ( )h(t ) d
计算。
如按式
t
r(t) 0 h( ) f (t ) d h(t) f (t)
计算。
例3 图示某电路的激励函数与冲激响应。求电路的零状态响应。
如按
t
r(t) f (t) h(t) 0 f ( )h(t ) d
δt
f
t
t
0
δ
f
t
d
0δ f 0
t d
f
t
δt f t f t
f tδt f t
δt
t0
f
t
t
0
δ
t 0
f
t
d
δ t0
t0
t0
f
t
d
f t t0
例1 求卷积 [e tε(t)] ε(t)
解： [e tε(t)] ε(t) t e ε( )ε(t )d 0
t ed 0
f ( )ε(t ) ε(t 2 )
f (2 )ε(t 2 ) ε(t 3 )
f (n 1) ε(t (n 1) ) ε(t n )
n1
f (k )ε(t k ) ε(t (k 1) ) k0
f (t) fa(t)
n1 k0
f
(k )ε(t
k )
1 e t
0
(t 0)
(t 0)
1 1 e t ε(t)
ቤተ መጻሕፍቲ ባይዱ
例2 设图示RC串联电路中电压源的电压
t
u(t) u0e T ε(t)
求零状态响应电压uC(t)。
解： 用卷积积分公式求uC(t)，应先求冲激响应

信号与系统
§2.6 卷积
信号与系统
§2.6.1 卷积定义
定义： 设有两个 函数 f1(t) f2 (t) ，积分
f (t) f1( ) f2(t )d
称为 f1(t) f2 (t) 的卷积积分，简称卷积，记为 f (t) f1(t) f2(t) 或 f (t) f1(t) f2(t)
t 0 , f2 ( ) 未移动 t 0 , f2 ( ) 右移 f2 (t ) t 0 , f2 ( ) 左移 f2 (t )
3
f2(t )
2
1 O 1 t3
t
下限
上限
f2(t )
t-3
t
f1( ) f2 (t ) -1
1
当
t
从
到
变化时，3对应的 2
f2(t )
从左向右移动。
f (t) f1( ) f2 (t )d
对τ延时t，
－(τ- t)= t- τ
积分结果为t 的函数
1.
积分变量改为
2.
f2(t)
f2 ( ) 反折
时延
f2( )
f2(t
)
3.相乘 f1( ) f2 (t )
4.乘积的积分 f1( ). f2 (t )d
信号与系统
§2.6.3 卷积图解过程
例 ：f1 (t )
f1
(Gt )2
(t
),
f2 (t )
t [u(t) 2
u(t
3)]
f1( )
1
1 O 1 t
f2(t )
3 2
t
t
1
1 O
f
1(
2
)
3
2
O

运用卷积的微积分性质，可以使卷积的运算大大简化 3、任意函数与冲激函数的卷积：
x(t)(t)x(t)
x(t) (t t0)x(t t0)
x ( t t0 )( t t1 ) x ( t t0 t1 )
4、经验公式：
x 1 ( t t0 ) x 2 ( t t1 ) x 1 ( t) x 2 ( t)t t t0 t1
22
1t2u(t)3(t1)2u(t1)3(t2)2u(t2)1(t3)2u(t3)
22
2
2
第2章 连续时间系统的时域分析
3.利用函数式计算卷积, 常见四种形式的积分限：
y(t) x( )h(t )d [一般的 x(t)和 h(t)]
u (t )
y(t) x( )h(t )d [有始的 x(t)和一般的 h(t)]
解：利用卷积的性质：
...
...
x(t) x0(t) T (t)
0T
t
x 0 ( t ) [ ( t mT )]
单位冲激串
m
x0 (t )
x 0 ( t ) ( t mT )
m
0
t
x 0 ( t mT )
m
第2章 连续时间系统的时域分析
第2章 连续时间系统的时域分析
0 tab 2(t)da 4(b t)2t0
ab 4
t2
3. i f 1 t2
a t-2 0 t 1
f1f20 1 ab 2(t)d a 4(tb )21 0
ab(2t 1) 4
4. i f 2 t3
t-2 0 1 t
f1f2
1ab(t)d
x 1 ( 1 )(t) t( u t) (t 1 )u (t 1 ) x1 ( 2)(t)1 2t2u(t)1 2(t1 )2u(t1 ) x 2 ( t ) t [ u ( t ) u ( t 1 ) ( 2 ] t ) u ( t [ 1 ) u ( t 2 )