当前位置：文档之家 › 海水运动基本方程

海水运动基本方程

  • 格式：pptx
  • 大小：1.62 MB
  • 文档页数：45

下载文档原格式

  / 45

合集下载

海水层流运动基本方程组

海水层流运动基本方程组

LOGO
二、盐量扩散方程
盐量：海水中所含溶质的质量，通常以s表示单
位质量海水中含的盐量。
出发点：盐量守恒定律 盐量守恒定律：溶于海水中的盐量在海水运动
过程中既不会自动产生也不会自动消失。
取一封闭曲面σ 所围成的空间，体积为τ 。
σ n
单位时间内τ内 盐量的变化
通过封闭曲面σ 随流动 进入空间τ 内部的盐量
第六节 基本方程的尺度分析和简化
LOGO
§1.2 海水层流运动基本方程组
一、 连续方程 二、 盐量扩散方程
三、 热传导方程
四、 状态方程
五、 海水层流运动基本方程组
LOGO
一、连续方程
出发点 ：质量守恒定律
质量守恒定律：海水在运动过程中，其总质量
保持不变，既不会自动产生，也不会自动消失。
海水受到压力效应与热力效应影响，其密度（或者 体积）是可以改变的，但是不能改变海水的质量。
物理海洋学 Physical Oceanography
§1 海水运动基本方程
Chapter 1 The equations of Motion
LOGO
§1海水运动基本方程——主要内容
第一节 海水运动方程 第二节 海水层流运动基本方程组
第三节 边界条件
第四节 时间平均的基本方程和边界条件
第五节 铅直平均的基本方程
s s s s u v w k D s t x y z u v w k t x y z
s, , p
LOGO
分子盐量扩散系数： k D
k

1.1109 m2 s 1
分子盐通量：
k D s
s k V s s t
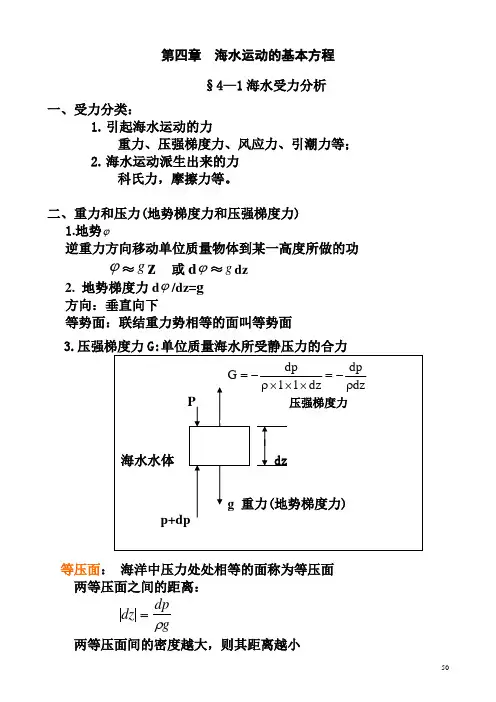
第四章 海水运动

第四章 海水运动

第四章 海水运动的基本方程 §4—1海水受力分析一、受力分类：1. 引起海水运动的力重力、压强梯度力、风应力、引潮力等； 2. 海水运动派生出来的力科氏力，摩擦力等。

二、重力和压力(地势梯度力和压强梯度力) 1.地势ϕ逆重力方向移动单位质量物体到某一高度所做的功ϕ≈g z 或d ϕ≈g dz2. 地势梯度力d ϕ/dz=g 方向：垂直向下等势面：联结重力势相等的面叫等势面3.压强梯度力G:单位质量海水所受静压力的合力等压面： 海洋中压力处处相等的面称为等压面 两等压面之间的距离：dz dp g =ρ两等压面间的密度越大，则其距离越小dz dpdz 11dp G ρ-=⨯⨯⨯ρ-= P 压强梯度力海水水体 dzg 重力(地势梯度力) p+dpG的方向：与等压面垂直；永远指向压力减小的方向。

G值的量级相当于无摩擦时，物体在lcm:1km斜面上所受的力. 正压场：等压面与等势面平行的压力场称为正压场斜压场：等压面相对等势面发生倾斜的压力场称为斜压场。

(a)正压场 (b) 斜压场内压场: 仅由ρ分布决定的压力场.t(温度)低t(温度)高s(盐度)高s(盐度)低ρ(密度)大ρ(密度)小外压场:由海面上的风、降水、江河径流等原因所产生的压力场总压场: 外压场迭加在内压场之上海洋上部: 斜压场某深度以下：正压场海洋上部海洋下部G的一般表达式Gdpdn n=-1ρ或G p=-∇1ρkzjyix∂∂+∂∂+∂∂=∇分量形式:Gpxx=-1ρ∂∂;Gpyy=-1ρ∂∂; Gpzz=-1ρ∂∂三.科氏力1. 地球表面的线速度差平均角速率ω＝7.292×10 5rad/s；曾母暗沙(4°N)：462m/s；漠河(53°25′)：276m/s；北极：0 m/s2. 傅科摆1851年傅科在67m长的钢丝下挂一个28kg的铁球组成一个单摆，他利用摆平面的转动成功地证明地球在自转。

傅科摆北极西东南极傅科摆摆动周期为T f =2πωϕsinω: rad/s；北京天文馆：9.6°/h，约230°/d南北两极: 360°/d T E=2πωT E:地球自转周期，86164s,称为一个恒星日也就是地球相对某一无限远的恒星自转的周期。

第七章 波浪理论及其计算原理

第七章 波浪理论及其计算原理

第七章 波浪理论及其计算原理在自然界中；常可以观察到水面上各式各样的波动，这就是常讲的波浪运动，它造成海洋结构的疲劳破坏，也影响船的航行和停泊的安全。

波浪的动力作用也常引起近岸浅水地带的水底泥沙运动，致使岸滩崩塌，建筑物前水底发生淘刷，港口和航道发生淤积，水深减小，影响船舶的通航和停泊。

为了海洋结构物、驾驶船舶和船舶停靠码头的安全，必须对波浪理论有所了解。

一般讲，平衡水面因受外力干扰而变成不平衡状态，但表面张力、重力等作用力则使不平衡状态又趋于平衡，但由于惯性的作用。

这种平衡始终难以达到，于是，水体的自由表面出现周期性的有规律的起伏波动，而波动部位的水质点则作周期性的往复振荡运动。

这就是波浪现象的特性。

波浪可按所受外界的干扰不同进行分类。

由风力引起的波浪叫风成波。

由太阳、月亮以及其它天体引起的波浪叫潮汐波。

由水底地震引起的波浪叫地震水波由船舶航行引起的波浪叫船行波。

其中对海洋结构安全影响最大的是风成波。

风成波是在水表面上的波动，也称表面波。

风是产生波动的外界因素，而波动的内在因素是重力。

因此，从受力的来看；称为重力波。

视波浪的形式及运动的情况，波浪有各种类型。

它们可高可低，可长司短。

波可是静止的一一驻波（即两个同样波的相向运动所产生的波，也可以是移动的——推进波以一定的速度将波形不变地向一个方向传播的波），可以是单独的波，也可以是一个接一个的一系列波所组成的波群。

§7-1 液体波动理论一、流体力学基础1、速度场 描述海水质点的速度随空间位置和时间的变化规律的一个矢量。

),,,(t z y x V V =它的三个分量为：x 方向的量：),,,(t z y x u u =y 方向的量：),,,(t z y x v v =z 方向的量：),,,(t z y x w w =2、速度势 对于作无旋运动的液体，存在一个函数，它能反映出速度的变化，但仅仅是反映速度大小的变化，这个函数称为速度v的势函数，简称速度势： ),,,(t z y x φφ=3、速度与速度势的关系x u ∂∂=φ， y v ∂∂=φ， zw ∂∂=φ 二、海水运动的基本假设1、海水无粘性，只有重力是唯一的外力；2、液体自由液面上的压力为常数；3、液体波动振幅相对于波长为无限小；4、液体作无旋运动。

基本方程的尺度分析和简化

基本方程的尺度分析和简化


U FL
U FL
P FUL
W 1 U ctg
Al FL2
Az FD 2
El
R0 : Rossby数
Ez
LOGO
Ekman数
二、尺度分析在基本方程简化中的运用
Rossby数：平流项与科氏力尺度相对大小。
U R0 FL
平流项/科氏力
U 1ms 1 , F 104 s 1
U 104 R0 FL L
所研究海区内任意点处的 f 值，在 0 处Taylor展开
f 2 sin 2 sin 0
df | 0 ( 0 ) d
y y0 r ( 0 )
df df dy df | 0 | 0 r | 0 d dy d dy
df df | 0 ( 0 ) | 0 ( y y0 ) d dy
果用最靠近的10的幂次数表示，就可以取作该物理量的概量。 来反映物理量在特定的物理过程中所具有的一般量值或大概 数值。
特征尺度：描述某种特定形式的运动有关物理量具有代
表意义的量值（一般大小），通常取为该物理量的最大值、 平均值或常见值。
LOGO
一、 尺度分析
因次（量纲）：代表物理量的一种符号，表示所要度量
在侧边界附近的Ekman深度范围内，水平和垂直湍 摩擦力与科氏力同量级，三者都必须考虑。
4）L<102m的小尺度运动，如果铅直尺度D Az F ，则有
El 1,
Ez 1
科氏力相对于湍摩擦力可以忽略
LOGO
二、尺度分析在基本方程简化中的运用
垂直运动方程的尺度分析
w w w w 1 p 2w 2w 2w u v w g fctgu Al ( 2 2 ) Az 2 t x y z z x y z
(海洋科学概论课件)第七章 海水运动的基本方程2

(海洋科学概论课件)第七章 海水运动的基本方程2


7
海洋中的波动
整个波包（由红色实线表示）则随位置和时间的变化而缓 慢变化。波包的速度称为群速度。波包在位置上周期性的 变化形成多个波包。群速度即是这些波包的速度。
2021/1/13
8
海洋中的波动
二、波浪类型(Wave types)
成因分： 风浪(wind wave)、涌浪(swell)、地震波、海啸(tsunami)、潮波、
wave) 动力机制：开尔文波(Kelvin wave)、罗斯贝波(Rossby wave)
2021/1/13
11
地震波和海啸
海洋中的波动
由海岸或海底地震造成海床垂直移动产生的波浪
EARTHQUAKES -----LANDSLIDES--------VOLCANOES
/Focus/ocean/motion/waves3.htm
海洋中的波动
波峰线方向单位宽度，自表至波动消失，一个波 长所具有的动能。
2021/1/13
40
二、波动能量(Wave energy) 3、总能量(total energy)：
海洋中的波动
4、能通量(flux of wave energy)： 在平均意义下，波动能量沿波浪传播方向的速率； 单位时间内在垂直波动传播方向的单位平面上，外
u v w 0 x y z
w tu w xv w yw w z 1 p zg
运动学边界条件： z0;
固体边界条件：Ｖｎ＝０
tV H w0
动力学边界条件：z=0, P = Pa(x,y,t)
2021/1/13
24
无旋运动：
V u ,v ,w
x y z
无旋运动的基本方程和边界条件：
ashs((hzk（ -(zd0k+)dz2） 0))2
海水状态方程式

海水状态方程式

海水状态方程式
contents
目录
• 海水状态方程式的定义 • 海水状态方程式的数学表达 • 海水状态方程式的实验验证 • 海水状态方程式的改进与优化 • 海水状态方程式的前景展望
01 海水状态方程式的定义
什么是海水状态方程式
描述海水压力与密度、温度等状态参数之间关系的数学表达 式。
用于计算在不同压力下海水的密度、声速、压缩性等物理属 性。
03 海水状态方程式的实验验 证
实验设备与材料
温度控制器
用于控制实验过程 中的温度。
密度计
用于测量海水的密 度。
压力容器
用于模拟不同深度 的海水压力。
盐度计
用于测 度和酸碱度。
实验步骤与过程
1. 准备实验材料
准备好所需的实验设备和材料，并确 保其精度和可靠性。
利用人工智能和机器学习技术对海洋数据进行处理和分析，能够发现隐藏的模式和规律， 为改进海水状态方程式提供新的思路和方法。
海水状态方程式在海洋科学中的应用前景
气候变化研究
海水状态方程式能够提供高精度、高分辨率的海洋状态数据，有 助于深入了解气候变化的原因和机制。
海洋生态系统研究
通过海水状态方程式模拟和预测海洋生态系统中的物质循环、能量 流动等过程，有助于更好地保护和利用海洋资源。
6. 重复实验
为了获得更准确和可靠的结果，可以 在相同条件下重复进行多次实验，并 对结果取平均值。
实验结果与结论
• 通过实验验证，可以获得不同条件下的海水状态方程式的实 验数据，并对这些数据进行分析和处理，以验证所提出的海 水状态方程式的准确性和可靠性。如果实验结果与理论预测 基本一致，则说明所提出的海水状态方程式是可靠的；如果 有较大偏差，则需要对方程式进行修正和完善。
纳维-斯托克斯方程构造海水模型

纳维-斯托克斯方程构造海水模型

纳维-斯托克斯方程构造海水模型纳维-斯托克斯方程是描述流体运动的基本方程之一，它采用了质量守恒、动量守恒和能量守恒三个方面的基本原理。

在海水的模拟中，纳维-斯托克斯方程可以用来描述海水的流动。

海水是一种自然的、复杂的流体，它受到多种因素的影响，包括风力、地球自转、潮汐、大气压力等。

因此，构造海水模型时需要考虑这些影响因素，将它们纳入到方程中。

纳维-斯托克斯方程可以从动量守恒方程推导得到。

动量守恒方程可以表示为：ρ(Du/Dt) = -∇P + ρg + μ∇^2u其中，ρ为海水的密度，u为海水速度矢量，P为海水的压力，g为重力加速度，μ为海水的粘性系数，∇为向量的梯度运算符，∇^2为向量的拉普拉斯运算符。

在海水模型中，通常会简化方程并进行假设。

例如，假设海水是不可压缩的，即密度不随时间和位置的变化而变化。

这样，动量守恒方程可以进一步简化为：(Du/Dt) = -∇P + g + μ∇^2u这个方程描述了海水速度的变化，其中∇P表示压力梯度对流体产生的影响；g表示重力加速度对流体产生的影响；μ∇^2u表示粘性系数对流体产生的影响。

海水模型还需要考虑边界条件和初始条件。

边界条件可以是固定边界条件，例如海岸线；或周期性边界条件，例如周期性潮汐。

初始条件可以是静止状态，也可以是给定的初始速度场。

为了求解纳维-斯托克斯方程，需要采用数值方法进行离散化。

常用的方法有有限差分法、有限元法和有限体积法等。

这些方法将海水模型离散化为网格，然后通过迭代求解离散化后的方程组，得到海水流动的数值解。

海水模型的构建还需要考虑其他与海水运动相关的参数，例如海水的温度、盐度、溶解氧等。

这些参数可以通过方程的源项来表示，例如热量传递、盐度传递和氧气传递等。

总之，纳维-斯托克斯方程是构造海水模型的基本方程之一。

通过对方程进行适当的简化和离散化，可以模拟海水的流动行为，并进一步研究海洋的物理和化学过程。

海水运动基本方程课件

海水运动基本方程课件

第四章 海水运动基本方程
精品
引言
• 一、研究对象：海水运动 • 二、研究目的
– 如何描述海水的运动 – 海水的运动是如何产生的 – 对不同形式的海水运动，哪些影响因子至关重要
• 三、描述海水运动状态和变化的基本变量 – 矢量场：速度（ u,v, w）
– 标量场：温度 、盐度 S 、密度 、压强 p
• 地球引力：地心对地球表面单位质量的海水微团的引力，
由海水微团指向地心。
F1 G K
ME r2
( r )（4-6） r
K 为引力常数：6.6720×10-11Nm2kg-2
• 惯性离心力：与地球自转有关的惯性力，是为在旋转坐标 系中应用牛顿第二定律而附加的力。方向垂直地轴，由地
轴指向海水微团
– 单位质量物体所受到科氏力：


F3 2 V （4-10）
• 性质：

– 大小： F3 2 V sin
– 科氏力的方向始终垂直于角速度和质点的运动方向。 – 在北半球，科氏力的水平分量总是指向运动右方。
精品
精品
3.压强梯度力
• 定义：单位质量水体所受的静压力的合力

k
ME r2
(
r r
)

g

k
ME r
c
– 惯性离心力位势
e

2R e
1 2R2 c 2
• 重力和g 重力位势的关系g e （4-9） 精品
2.科氏力（地转偏向力）
• 定义：与地球自转有关的惯性力。当质点以一定 速度相对于旋转坐标系（非惯性坐标系）运动时， 才产生。
– 在x方向上压力的合力

p
海水运动基本方程

海水运动基本方程


(τ 2 − τ 1 )δ x δ y
v dV du τ =µ =µ பைடு நூலகம்n dz
∂ ∂u Fx = ( µ ) ∂z ∂z
• 单位体积海水微团在x方 向上所受应力合力为：
(τ
2
− τ 1 )δ x δ y τ 2 −τ1 = δxδyδz δz
• 若分子粘性系数为常量，单位质量海水微团在x方向上受到 的应力合力为： 1 ∂ 2u Fx = µ 2 ρ ∂z • 若海水微团在各个方向上都有速度，并都有速度梯度，单 位质量海水微团受的应力合力的三个分量为： 单位质量海水微团受的 1 ∂ 2u ∂ 2u ∂ 2u µ Fx = µ 2 + 2 + 2 = ∆u 摩擦力的矢量形式 ρ ∂x ∂y ∂z ρ
哈密顿算符
∇= ∂ ∂ ∂ i+ j+ k ∂x ∂y ∂z
• 地球引力和惯性离心力都是位势力
v ME r ME +c – 地球引力位势 ∇φ g = k 2 ( ) ⇒ φ g = − k r r r v 1 2 2 2 – 惯性离心力位势 ∇φe = −Ω R ⇒ φe = − Ω R + c 2
L D
对P点，单位质量所受的惯性离心力的势 v v v MM D MM v ϕ 2 = − ∫ N ⋅ dr = − ∫ K 2 ( ) ⋅ dr = K 2 r cos θ + c2 D D D 设地心处的势为0，则 M ϕ 2 = K M r cosθ 2
D
对P点，单位质连所受月球引潮势 月球引潮势： 月球引潮势
（4-8）
v R=
v r v v v r cos ϕ r = r海表面 + z ( ) r
海水运动方程讲义

海水运动方程讲义


在 t 时间间隔内：
在惯性坐标系O-XYZ中，观测到的绝对位移：
PP va t
在旋转坐标系O-xyz中，观测到的相对位移：
PP v t
由O-xyz相对于O-XYZ旋转带来的牵连位 移：
2
PP ve t
1LOGO
二、描述海水运动的坐标系
PP PP PP
a e
v const da A d A A d d r d dt dt ( r ) r d dt dt dt (v r ) (v r ) dt v dv d ( r ) v ( r ) dt dt dv 2 v ( r ) d a va d dt v 2 v ( r ) dt dt LOGO
于流体性质
存在速度梯度才产生分子粘性力，当两层流体以相同的速 度运动或处于静止状态时，是不会产生切应力的。
LOGO
三、作用在海水微团上的力
z
摩擦力的表达形式：
假设海水只沿x方向运动， 且只在z方向有速度梯度 立方体四个侧面的切应力为0 上下两个面受到的切应力的合力为：
y
δy δz
τ1
u
τ2 δx x
指向压力减小的方向；压强梯度力是产生运动的力。
LOGO
三、作用在海水微团上的力
压强p的确定：
p pa x,表大气压强 海水任意深度处压强：与海水 本身结构和运动有关
pa往往取常量,也有特殊情况。 pw：内压场、外压场、总压场。 一般情况下，pa和pw的具体形式有待确定，之后压强 梯度力也便确定。
由海水微团指向地心。
F1 G k ME r ( ) 2 r r
海水层流运动基本方程组

海水层流运动基本方程组


分子盐量扩散系数： k D
k

1.1109 m2 s 1
分子盐通量：
k D s
s k V s s t
盐量随时间的 变化量
平流产生 的盐通量
分子盐通 量
LOGO
三、热传导方程
单位时间内空间τ内 的热量变化

：温度
Q
C p t
d
C p ：定压比热。在一定压强下，单位质
V V
若认为海水是不可压缩的 流体微团在运动过程中，形 状可以发生变化，但体积从 而其所含海水密度不变
即：
d 0 dt
d V 0 dt
质量连续方程
u v w V 0 即： 0 x y z
体积连续方程


s sV S 0 t s s V s s ( V ) S 0 t t
S ks S ( k s )
k ( s ) k s
第六节 基本方程的尺度分析和简化
LOGO
§1.2 海水层流运动基本方程组
一、 连续方程 二、 盐量扩散方程
三、 热传导方程
四、 状态方程
五、 海水层流运动基本方程组
LOGO
一、连续方程
出发点 ：质量守恒定律
质量守恒定律：海水在运动过程中，其总质量
保持不变，既不会自动产生，也不会自动消失。
海水受到压力效应与热力效应影响，其密度（或者 体积）是可以改变的，但是不能改变海水的质量。
为了简化
忽略与p有关项， s变化不大情况下（如大洋），忽略与s有关项
0 1 K

05-1 海流基本方程28

湍流粘滞系数K大于 2~3个量级 考虑海水在各运动方向上的速度梯度，则湍流摩擦力：
Fx
1 u 1 u 1 Kx + Ky + x x y y
u z Kz z
6
海水微团受力
重力
地心引力和地球自转所产生的惯性离心力的合力。 单位质量海水所受的重力即为重力加速度g，理论上它是地理纬度φ和海 洋深度z的函数，但在海洋学中一般将其视为常量。
与重力处处垂直的面称为等位势面，静止状态下的海平面就是一个等势 面。相距dz(m)的两个等势面之间的位势差dΦ，定义为将单位质量海水从 一个等势面逆重力方向移动至另一个等势面时重力所作的功，即dΦ=gdz， 单位为位势米(gpm)，1(gpm)=1/9.8g(m)。可见在数值上1位势米近似等于1 几何米。通常以静止状态下的海平面为0位势面，海面以下的位势面与其 位势差称为位势深度；海面以上的位势面与其位势差则称为位势高度。
故
dV w 2 r dt
单位质量物理所受惯性离心力Fcf = w2r
12
海水微团受力
科氏力
W
z y 对于单位质量的静止物体 地球任意纬度的惯性离心力 Fcf = W2R
R
0
x
θ
a
13
海水微团受力
科氏力
对于向东运动的单位质量海水微团
ω
t1 t2 t3 t1 t2
其旋转角速度应为W+u/R 则在旋转地球上 该微团受到的惯性离心力 Fcf = (W+u/R)2R Fcf = W2R +2(Wu/R)R +(u/R)2R 静止 运动 忽略
海流一般以带箭头的线段表示，箭矢方向指海水的去向，线 段长短表示海流的大小，单位m/s或Kn。 1纬距＝111.1km=60海里 1节（ Kn ）＝1海里／小时＝1.85233km/小时

第五讲-海洋环流基础知识


37
北纬25度的流速？
u 1 p ρ f = 2 z ρ z y
38
东经150度的流速？
v 1 p ρ = 2 f z ρ z x
39
热成风——大洋中的Beta螺旋
40
第六节 泰勒-普劳德曼定理
涡度方程中如果运动达到定常状态，同时外 力作用可以忽略（大尺度运动），斜压项为0 （正压流体）： 忽略相对涡度：
2. 涡度方程
对运动方程求旋度，得到涡度方程
dω a dω ρ × p F = = ω a u ω a u + +× 2 dt dt ρ ρ
涡度的变化 内部作用 斜压作用
外力作用
涡度方程表明：涡度的变化由内因、斜压作 涡度的变化由内因、 涡度的变化由内因 用和外因共同决定， 用和外因共同决定，绝对涡度的变化和相对 涡度的变化一样。 涡度的变化一样。
33
简化形式的热成风关系
u 1 p ρ f = 2 热成风关系构建了垂 z ρ z y 直流速的变化和水平 垂直流 水平密 密度（温度）变化之 速剪切 度梯度 间的关系，是大洋中 v 1 p ρ 非常重要的流速和密 f = 2 度（温度）的关系式 z ρ z x
34
热成风关系应用
p ρ p0 f0 z y u 1 p ρ f = 2 f0 z ρ z y
27
涡度变化原因1——内部作用
内部作用表达式： ω a u ωωa ui + vj + wk ωa k + + z x y z r u r v r u v = i ωa + j ωa k + z z x y
流体柱的垂直流速 流体柱的辐合辐 剪切导致涡度变化 散导致涡度变化

物理海洋学概论- 运动方程式


d 0 dt dS 0 dt
for mass for salt

以上，我們有五組方程式(三個運動方程、質量守恆及鹽 度守恆)，但有六個變數(u, v, w, p, , S)要解，故仍需一 組方程式求解。 狀態方程式，描述壓力與溫度、鹽度之間的關係： =(S,T,P) 除了質量與鹽度守恆外，運動亦要求能量及渦度守恆。

其可以向量形式，較簡短表示：
du ut (V )u dt dv vt (V )v dt dw wt (V ) w dt

du u (u )u 或更簡短： dt t

簡單介紹各種不同的力： 水平壓力梯度力 (horizontal pressure gradient) - body force，整個水體能夠立即感受到的力。 - 水往低處流，由高壓流向低壓。 - du 1 p others dt x
2007.10.15

海水運動的能量來自於太陽的熱。 海水的運動：紊流、波浪引起的流、潮流、風吹流、 溫鹽環流、湧升/下沉流…等。 海流觀測：航海者回報、浮標追蹤、錨碇式觀測、 移動式觀測、水文推算、衛星推測…等。 數學是簡單用來描述海水運動的工具。




運動方程式 (Equations of Motion) 守恆方程式 (Conservation Equations) 質量守恆 (Conservation of mass) 鹽度守恆 (Conservation of salt) 渦度守恆 (Conservation of potential vorticity) 連續方程式 (Continuity Equation)

剛體與流體? 古典物理考慮單一質點，其形狀在運動過程中不會改變(剛體)，故質點運動的加速度， 簡單的可以速度對時間的變化表示： d u ຫໍສະໝຸດ u dt t表示

《海洋地理学》第七讲 海洋环流

在北半球垂直于压强梯度力指向梯度力
重力
3 地转流
三、地转流场与密度场、质量场之间的关系
海洋中的密度变化是连续的，因此，由于海水密度分布不 均匀产生斜压场引起的地转流场的变化也应当是连续的。 当海水上层流速大于下层流速时，我们顺流而立，则在北 半球密度小的海水在右侧，密度大的海水在左侧，等压面 自左下向右上倾斜。在南半球则相反。
可以根据大洋上层等温面（线）或等盐面（线）的倾斜方 向定性推断地转流的方向。
3 地转流
四、地转流的动力计算方法
借助于海洋调查中的温度、盐度和深度（压力）资料，根 据海水状态方程，首先计算海水的密度或比容，进而计算 等压面之间的位势差，再进行地转流的计算。
海兰－汉森公式
适应于内压场引起的地转流。 海底为流速参考零面。
北半球，西风漂流是日本暖流和墨西哥湾暖流的延续，分别称为北 大西洋暖流和北太平洋暖流。由于这两股暖流的海水是从大洋西部的低 纬度流来的，故属暖流性质。 南半球，各大洋的西风漂流连在一起，形成了全球性环流，其性质 属寒流，原因是： 1、南半球的西风漂流是环绕南极大陆流动的，而南极大陆是一个 冰雪覆盖的大陆，气温极低，影响周围水域的温度 2、南极大陆延伸出来的冰舌，进入海面后形成了漂浮的冰山，这 些浮冰融化时吸收大量的热能，从而使海水的温度降低 3、南极大陆的强劲而干冷的极地东风也加剧了海水的降温
4、《真腊风土记》(元)记载：① 自温州开船，西南行，历闽、广 海外诸州港口，过七洲洋，经交 趾洋到占城。又自占城顺风可半 月到真腊；②真腊四时常如五六 月天，不识霜雪，半年有雨，半 年绝无；③信教者削发穿黄，偏 袒右肩，其下系黄布裙，跣足。 据此并结合图1，回答下题。
4 风海流
三、风海流的体积运输

地转流计算解读


课堂讲评
• 练习1 AB位于南半球，A站比B站高，A→B
v AB
gtg 2 sin
A B
20°
h 9.8 3 200 10 1 2 7.3 105 sin 21 h 0.93m
22°
注：南半球地转流流向指向等压面下倾方向左方90°
练习2
y
2 V vx v2 y
2 V vx v2 y 2.9 m / s
o vy

vx x V
等压面下倾方向 X方向：由o→x Y方向：由o→y 北半球
vy arctg 26 vx
练习3 计算步骤 (1) 划分计算的层次 (2) 假设一个适当的零面 (3) 求出hP-PN(三步近似） (4) 求Vp (5) 作图
v
u
2 AB
v
2 AB
y
A
uAB B uBC C x U合
方向也是合成的方向
d) 动力计算在不同的参考零面下所得结果是 不同的，因此选取适当的零面是十分重要。
课堂练习
• 练习1 右图表示海区有地转流流速1m/s， 问A、B两站哪一站的海面较高？ 高多少？（注：AB连线与流向垂 直，AB相距200km） • 练习2 假设30°N某海面的倾斜是：沿X方 向每增加1km，海面下降1cm；沿Y 方向每增加1km，海面下降2cm。求 此海域地转流流向及流速，并已箭 号表示于下图. A B
方程右边：作用在 单位质量海水质点 上的力
du p u u u 2 sin ( K x ) ( K y ) ( Kz ) dt x x y y z z x dv p v v v 2 sin u ( K x ) ( K y ) ( Kz ) dt y x y y z z x
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
x
– 在x方向上压力的合力： – 在y方向上压力的合力： – 在z方向上压力的合力：
作用在整个海水微团上的压力合力：
p xyz
x
p xyz
y
p xyz
z


p x
i
p y
j
p z
kxyz
作用在单位质量上的压强梯度力：
v

2
R
惯性力 单位质量 科氏力 惯性
水体所受合力
离心力
（4-5a） （4-5b）
运动的海水微团所受的力
• 重力（地球引力，惯性离心力），科氏力（地转偏向力）， 压强梯度力，摩擦力，引潮力
• 分类1：
– 引起海水运动的力 – 海水运动后派生的力
• 分类2：
– 质量力（体积力）：作用在组成海水微团的所有质量上，与海水微团 质量或者体积成比例，与海水微团质量或体积成正比，而与海水微团 以外的海水介质的存在无关。
dV dt
i
Fi 2 2 R

G
2R
2 V
1

p


V
T
• 运动方程的向量形式：
dV dt

1

p

2 V
g

V
T
（4-19）
五、球坐标系下运动方程的标量形式
• 1. 球坐标系
•此地理位置可以 用球坐标系中的
向上的速度梯度成正比

dV
dn
– 其中 为动力的分子粘性系数，单位N·s·m-2
• 设海水只沿x方向运动， 且只在z方向上存在速度 梯度
• 立方体侧向四个面的切应 力为0，上下两面受到的 总应力为：
( 2 1 )xy
• 单位体积海水微团在x方 向上所受应力合力为：
( 2 1 )xy 2 1
r
r r海表面 z(
r) r
z0
g(, z) gc g(, z) 9.80616 0.025928cos 2 0.00069 cos2 2
0.0000003086z
（ms-2）
• 位势力：若某力对物体做的功与物体运动的路径
无关，只决定于物体的初始位置和终止位置。
• 重力和g重力位势的关系g e （4-9）
2.科氏力（地转偏向力）
• 定义：与地球自转有关的惯性力。当质点以一定 速度相对于旋转坐标系（非惯性坐标系）运动时， 才产生。
– 单位质量物体所受到科氏力：
F3 2 V （4-10） • 性质：
– 大小： F3 2 V sin
di
dj
dk
i j k u v w
dt dt dt dt
dt dt dt
设任一向量场变量
A(,
,r
,
t)或

A(,, r,t)
dA
A
dt

A
d

A
d

A
dr
t r



dA A A d A d A dr
经度 、纬度 、
r 与地心的距离
表示。
2. 球坐标系下的速度
V ui vj wk
u

r
cos
d
dt
R
v

r
d
dt
w

dr dt
（4-20）
R

R
3. 球坐标系下的加速度
对速度矢量求微商：
dV
du dv dw

V

V

（4-12）
其中

为：
运动的分子粘性系数
单位：m2·s-1
拉普拉斯算子
2 2 2 x 2 y 2 z 2
5. 引潮力
• 天体引潮力：主要包括月球引潮力和太阳引潮力。 • 月球引潮力：地球绕地月公共质心公转所产生的公转惯性
离心力和月球引力的合力。 • 月球引力：地球上任意点单位质量的物体所受的月球引力方
性质：
p xyz
F4


1

p
（4-11）
1）压强梯度力与等压面垂直，指向压力减小的方向； 2）压强梯度力是产生运动的力。
4.摩擦力（分子粘性力，切应力）
• 定义：当两层流体做相对运动时，由于分 子粘性在其界面上产生的一种切向作用力。
• 性质：
– 属于表面力，是运动派生的力 – 单位面积的切应力与界面（两层流体之间）法
• 惯性离心力：与地球自转有关的惯性力，是为在旋转坐标
系中应用牛顿第二定律而附加的力。方向垂直地轴，由地
轴指向海水微团
F2 2R （4-7）
• 重力加速度
单位质量物体所受重力
g
F1
F2

G
2R
R

K
ME r2
rcos
(
r)

2
R
（4-8）
向为从物体所在位置指向月球中心，大小为： KM m L2
惯性离心力
地球绕地月 公共质点O 平动公转
地球上各点所 受到的公转惯 性离心力大小 和方向都相同
单位质量的
惯性离心力

N
0 2r0


0
2
r0
(
D D
)
在地球质心，所 受月球引力与惯 性离心力大小相 等，方向相反
公转惯性离心力
• 在地-月系中，地球除了自转运动外，还绕地月公共质心公转，这种公转为
2u x 2

2u y 2

2u
z
2

ຫໍສະໝຸດ u单位质量海水微团受的 摩擦力的矢量形式
Fy

1



2v x 2

2v y 2

2v
z
2



v
Fz

1



2w x 2

2w y 2

2w
z 2



w
F5
d a va

dv
2
v

2
R
（4-4）
dt dt
绝对 相对 科里奥利 向心
三、作用在海水微团上的外力
• 根据牛顿第二定律： a
Fi
dava

dv
2
v

2
i R
dt dt
i
Fi
在旋转坐标系下：
dv
dt
i
Fi

2
– 科氏力的方向始终垂直于角速度和质点的运动方向。 – 在北半球，科氏力的水平分量总是指向运动右方。
3.压强梯度力
• 定义：单位质量水体所受的静压力的合力
– 在x方向上压力的合力

p

p x
(
1 2
x)

yz


p

p x
(
1 2
x)
yz
p xyz
2. 旋转坐标系下的速度
• •
在惯性坐标系 在旋转坐标系
O
o
XYZ
xyz
中，观测的绝对位移为：PP '' 中，观测的相对位移为：P ' P ''
vvtat
PP'' P'P'' PP' vat vt vet va v ve vdearvadvRrrrr（4-1）
地球上任一点P所受到月球的引潮力为：
FM

KM
M
(
1 D2
D D
1 L2
L) L
（4-15）
• 引潮势：
对P点，单位质量所受的月球引力的势：

1 K (P) dL
K
MM L2
(
L)

dL
K
M
M
L
L
c1
设地心处位势为0，则
1

KM
M
(1 L
一、海水运动方程的出发点
• 海水微团
• 质点运动学和动力学
• 牛顿定律
– 物质具有保持其速度不变的性质—惯性
– 力是产生加速度的原因
a
F/
m
牛顿定律—经典力学—惯性坐标系
二、描述海水运动的坐标系
• 1. 惯性坐标系
什么是惯性坐标系？ 固定在地球上的坐标系是惯性坐标 系吗？ • 符合惯性定律的参照系称为惯性参考 系。固定在惯性参考系上的坐标，即 惯性坐标系 • 固定在地球上的坐标系称为旋转坐标 系，是非惯性坐标系，牛顿定律不成 立。
r cos

KM
M
(
1 L

1 D

r D2
cos
)
（4-16）
对P点，单位质量所受太阳引潮势：
S

KM
S
(
1 LS

1 DS

r DS 2
cos S )
天体引潮势：
（4-17）
T M S
天体引潮力：

F6 FT T
（4-18）
四、运动方程的向量形式

xyz
z

dV du
dn dz
Fx

z