流体流动方程
- 格式:ppt
- 大小:1.12 MB
- 文档页数:54



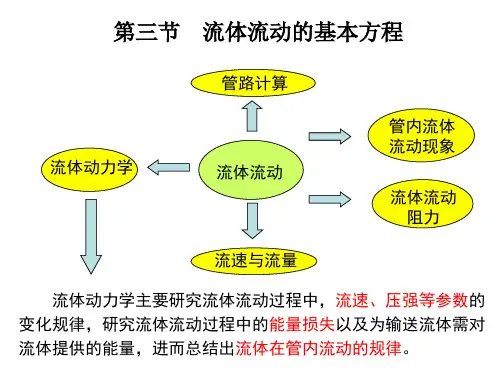
第二节 流体流动的基本方程式化工厂中流体大多是沿密闭的管道流动,液体从低位流到高位或从低压流到高压,需要输送设备对液体提供能量;从高位槽向设备输送一定量的料液时,高位槽所需的安装高度等问题,都是在流体输送过程中经常遇到的。
要解决这些问题,必须找出流体在管内的流动规律。
反映流体流动规律的有连续性方程式与柏努利方程式。
1-2-1 流量与流速一、流量单位时间内流过管道任一截面的流体量称为流量。
若流体量用体积来计量,称为体积流量,以V s 表示,其单位为m 3/s ;若流体量用质量来计量,则称为质量流量,以w s 表示,其单位为kg/s 。
体积流量与质量流量的关系为:w s =V s ·ρ (1-16) 式中 ρ——流体的密度,kg/m 3。
二、流速单位时间内流体在流动方向上所流经的距离称为流速。
以u 表示,其单位为m/s 。
实验表明,流体流经管道任一截面上各点的流速沿管径而变化,即在管截面中心处为最大,越靠近管壁流速将越小,在管壁处的流速为零。
流体在管截面上的速度分布规律较为复杂,在工程计算中为简便起见,流体的流速通常指整个管截面上的平均流速,其表达式为: A V u s = (1-17)式中 A ——与流动方向相垂直的管道截面积,m 2。
流量与流速的关系为:w s =V s ρ=uA ρ (1-18) 由于气体的体积流量随温度和压强而变化,因而气体的流速亦随之而变。
因此采用质量流速就较为方便。
质量流速,单位时间内流体流过管路截面积的质量,以G 表示,其表达式为:ρρu A V A w G s s === (1-19)式中 G ——质量流速,亦称质量通量;kg/(m 2·s )。
必须指出,任何一个平均值都不能全面代表一个物理量的分布。
式1-17所表示的平均流速在流量方面与实际的速度分布是等效的,但在其它方面则并不等效。
一般管道的截面均为圆形,若以d 表示管道内径,则 24d V u s π= 于是 uV d sπ4=(1-20) 流体输送管路的直径可根据流量及流速进行计算。


化工原理流体流动知识点总结化工原理中的流体流动是指在化工过程中物质(气体、液体或固体颗粒)在管道、设备或反应器中的运动过程。
了解流体流动的知识对于化工工程师来说至关重要。
下面是关于流体流动的一些重要知识点的总结。
1.流体的物理性质:-流体可以是气体、液体或固体颗粒。
气体和液体的主要区别在于分子之间的相互作用力和分子间距。
-流体的物理性质包括密度、黏度、表面张力、压力和流速等。
2.流体的运动方式:- 流体的运动可以是层流(Laminar flow)或紊流(Turbulent flow)。
-在层流中,流体以平行且有序的方式流动,分子之间的相互作用力主导着流动。
-在紊流中,流体以非线性和混乱的方式运动,分子之间的相互作用力相对较小,惯性和湍流运动主导着流动。
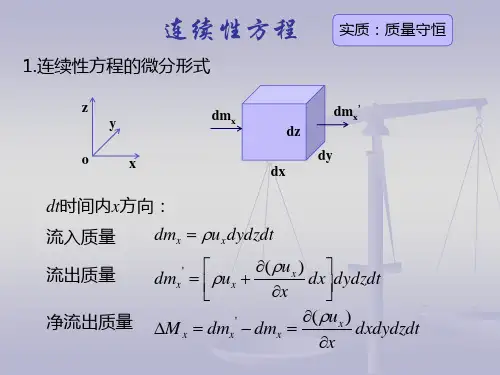
3.流体的流动方程:-流体流动可以通过连续性方程、动量方程和能量方程来描述。
-连续性方程(质量守恒方程)描述了流体在空间和时间上的质量守恒关系。
-动量方程描述了流体中的力平衡关系,包括压力梯度、黏度和惯性力等因素。
-能量方程描述了流体中的能量守恒关系,包括热传导、辐射和机械能转化等因素。
4.管道流动:-管道中的流体流动可以是单相(单一组分)或多相(多个组分)。
-管道流动的主要参数包括流速、压力损失和摩阻系数等。
- 常用的管道流动方程包括Bernoulli方程、Navier-Stokes方程和Darcy-Weisbach方程等。
5.流体输送:-流体输送是指将流体从一个地点输送到另一个地点的过程。
-在流体输送中,常用的设备和装置包括泵、压缩机、阀门、流量计和管道系统等。
-输送过程中要考虑流体的性质、流速、压力损失以及设备的选型和操作条件等因素。
6.流体混合与分离:-流体混合和分离是化工过程中常见的操作。
-混合可以通过搅拌、喷淋、气体分散等方法实现。
-分离可以通过过滤、沉淀、蒸馏、萃取和膜分离等方法实现。
7.流体力学实验:-流体力学实验是研究流体流动和相应现象的方法之一-常用的流体力学实验包括流速测量、压力测量、流动可视化和摩擦系数测定等。

流体流动状态与伯努利方程
流体力学伯努利的方程是p+1/2ρv2+ρgh=C。
p为流体中某点的压强,v为流体该点的流速,ρ为流体密度,g 为重力加速度,h为该点所在高度,C是一个常量。
它也可以被表述为p1+1/2ρv12+ρgh1=p2+1/2ρv22+ρgh2。
扩展资料:
使用伯努利定律必须符合以下假设,方可使用;如没完全符合以下假设,所求的解也是近似值:
1、定常流:在流动系统中,流体在任何一点之性质不随时间改变。
2、不可压缩流:密度为常数,在流体为气体适用于马赫数(Ma)<0.3。
3、无摩擦流:摩擦效应可忽略,忽略黏滞性效应。
4、流体沿着流线流动:流体元素沿着流线而流动,流线间彼此是不相交的。
参考资料来源:百度百科—伯努利原理。

第二节 流体流动的基本方程式化工厂中流体大多是沿密闭的管道流动,液体从低位流到高位或从低压流到高压,需要输送设备对液体提供能量;从高位槽向设备输送一定量的料液时,高位槽所需的安装高度等问题,都是在流体输送过程中经常遇到的。
要解决这些问题,必须找出流体在管内的流动规律。
反映流体流动规律的有连续性方程式与柏努利方程式。
1-2-1 流量与流速一、流量单位时间内流过管道任一截面的流体量称为流量。
若流体量用体积来计量,称为体积流量,以V s 表示,其单位为m 3/s ;若流体量用质量来计量,则称为质量流量,以w s 表示,其单位为kg/s 。
体积流量与质量流量的关系为:w s =V s ·ρ (1-16) 式中 ρ——流体的密度,kg/m 3。
二、流速单位时间内流体在流动方向上所流经的距离称为流速。
以u 表示,其单位为m/s 。
实验表明,流体流经管道任一截面上各点的流速沿管径而变化,即在管截面中心处为最大,越靠近管壁流速将越小,在管壁处的流速为零。
流体在管截面上的速度分布规律较为复杂,在工程计算中为简便起见,流体的流速通常指整个管截面上的平均流速,其表达式为: A V u s = (1-17)式中 A ——与流动方向相垂直的管道截面积,m 2。
流量与流速的关系为:w s =V s ρ=uA ρ (1-18) 由于气体的体积流量随温度和压强而变化,因而气体的流速亦随之而变。
因此采用质量流速就较为方便。
质量流速,单位时间内流体流过管路截面积的质量,以G 表示,其表达式为:ρρu A V A w G s s === (1-19)式中 G ——质量流速,亦称质量通量;kg/(m 2·s )。
必须指出,任何一个平均值都不能全面代表一个物理量的分布。
式1-17所表示的平均流速在流量方面与实际的速度分布是等效的,但在其它方面则并不等效。
一般管道的截面均为圆形,若以d 表示管道内径,则 24d V u s π= 于是 uV d sπ4=(1-20) 流体输送管路的直径可根据流量及流速进行计算。


不可压缩流体流动的变化方程不可压缩流体流动的变化方程是描述流体在时间和空间上的变化规律的方程。
它由连续性方程和动量方程组成。
一、连续性方程:不可压缩流体的连续性方程描述了流体质点的质量守恒关系。
在稳态条件下,连续性方程可以表示为:∇·v = 0其中,∇表示空间的梯度算子,v表示流体的速度矢量。
该方程表示了流体通过任意闭合曲面的净质量变化为0,即质量进出的总和为0。
二、动量方程:不可压缩流体的动量方程描述了流体质点的运动定律。
在稳态条件下,动量方程可以表示为:ρ(v·∇)v = -∇P + ρg + μ∇²v其中,ρ表示流体的密度,P表示流体的压强,g表示重力加速度,μ表示流体的动力粘度,∇²表示速度矢量的拉普拉斯算子。
该方程中的第一项ρ(v·∇)v表示流体的非定常惯性项;第二项-∇P表示压力梯度对流体运动的影响;第三项ρg表示重力对流体运动的影响;第四项μ∇²v表示粘性对流体运动的影响。
这些项分别描述了流体质点的加速度、压力力、重力力和粘性力对流体动量变化的影响。
不可压缩流体的动量方程中的非定常惯性项通常可忽略,从而简化为:-∇P + ρg + μ∇²v = 0这个方程可以解释流体在压强梯度、重力和粘性力的作用下的运动。
上述的连续性方程和动量方程是描述不可压缩流体流动的基本方程。
在进行实际计算时,通常还要考虑边界条件、流体的特性以及相应的求解算法等因素。
此外,流体的温度、浓度等其他因素也可以加入到动量方程中,形成相应的耦合方程,用于解决特定问题。
总之,不可压缩流体流动的变化方程是描述流体在时间和空间上变化规律的方程,它由连续性方程和动量方程组成,能够更全面地揭示不可压缩流体的运动定律。
流体力学流速计算公式一、伯努利方程推导流速公式(理想不可压缩流体定常流动)1. 伯努利方程。
- 对于理想不可压缩流体作定常流动时,在同一条流线上有p+(1)/(2)ρ v^2+ρ gh = C(p是流体压强,ρ是流体密度,v是流速,h是高度,C是常量)。
- 假设水平流动(h_1 = h_2),则方程变为p_1+(1)/(2)ρ v_1^2=p_2+(1)/(2)ρ v_2^2。
- 由此可推导出流速公式v_2=√(v_1^2)+(2(p_1 - p_2))/(ρ)。
2. 适用条件。
- 理想流体(无粘性),实际流体在粘性较小时可近似使用。
- 不可压缩流体,像水在大多数情况下可视为不可压缩流体,气体在低速流动时也可近似为不可压缩流体。
- 定常流动,即流场中各点的流速等物理量不随时间变化。
3. 示例。
- 已知水管中某点1处的压强p_1 = 2×10^5Pa,流速v_1 = 1m/s,另一点2处的压强p_2 = 1.5×10^5Pa,水的密度ρ = 1000kg/m^3。
- 根据v_2=√(v_1^2)+(2(p_1 - p_2))/(ρ),将数值代入可得:- v_2=√(1^2)+frac{2×(2×10^{5-1.5×10^5)}{1000}}- 先计算括号内的值:2×(2×10^5-1.5×10^5)=2×5×10^4=10^5。
- 则v_2=√(1 + 100)= √(101)≈10.05m/s。
二、连续性方程推导流速公式(不可压缩流体定常流动)1. 连续性方程。
- 对于不可压缩流体的定常流动,有S_1v_1 = S_2v_2(S_1、S_2分别是流管中两个截面的面积,v_1、v_2是相应截面处的流速)。
- 由此可推导出流速公式v_2=(S_1)/(S_2)v_1。
2. 适用条件。
- 不可压缩流体,如液体或低速流动的气体。
流体力学中的流体流动方程流体力学是研究流体运动行为的学科,其中涉及到的重要概念之一就是流体流动方程。
流体流动方程是描述流体流动中物理量随时间和空间的变化关系的数学模型。
本文将详细介绍流体力学中的流体流动方程,包括连续性方程、动量方程和能量方程等各个方面。
1. 连续性方程连续性方程是描述流体质量守恒的基本方程。
它的数学表达式为:\[ \frac{{\partial \rho}}{{\partial t}} + \nabla \cdot (\rho \mathbf{v}) = 0 \]其中,\(\rho\) 表示流体的密度,\(\mathbf{v}\) 表示流体的速度矢量。
该方程表示了流体质量的变化率与流体速度和流体密度的关系。
通过连续性方程,我们可以了解到在流体流动过程中,质量的变化与流速的关系。
2. 动量方程动量方程是描述流体运动动力学性质的方程。
它的数学表达式为:\[ \rho \left( \frac{{\partial \mathbf{v}}}{{\partial t}} + \mathbf{v}\cdot \nabla \mathbf{v} \right) = - \nabla P + \mu \nabla^2 \mathbf{v} +\rho \mathbf{g} \]其中,\(P\) 表示流体的压力,\(\mu\) 表示流体的动力粘度,\(\mathbf{g}\) 表示重力加速度。
该方程描述了流体运动过程中的力和速度的关系,包括压力、粘度和重力等因素的影响。
3. 能量方程能量方程是描述流体能量守恒的方程。
它的数学表达式为:\[ \rho \left( \frac{{\partial e}}{{\partial t}} + \mathbf{v} \cdot \nabla e \right) = - P \nabla \cdot \mathbf{v} + \nabla \cdot (\mu \nabla \mathbf{v}) + \rho \mathbf{g} \cdot \mathbf{v} + Q \]其中,\(e\) 表示流体的单位质量内能,\(Q\) 表示单位质量的流体所受到的热量。