随机过程第四章(1)

1第四章 马尔可夫过程内容提要1. 马尔可夫过程的概念 （1）马尔可夫过程给定随机过程{}(),X t t T ∈，如果对122,∀≥∀<<<∈n n t t t T ，有11221111{()|(),(),,()}{()|()}n n n n n n n n P X t x X t x X t x X t x P X t x X t x ----<====<=则称{}(),X t t T ∈为马尔可夫过程。

称(){}:,==∈E x X t x t T 为状态空间。

参数集和状态空间都是离散的马尔可夫过程称为离散参数马氏链. 参数连续、状态空间离散的马尔可夫过程称为连续参数马氏链. （2）k 步转移概率设{}(),0,1,2,=X n n 为离散参数马氏链，称()(),(,){|},0,1=+==≥≥i j p n k P X n k j X n i n k为{}(),0,1,2,=X n n 在时刻n 的k 步转移概率，称(),(,)((,)),P =∈i j n k p n k i j E为{}(),0,1,2,=X n n 在时刻n 的k 步转移概率矩阵. 特别地，当1k =时，在时刻n 的一步转移概率和一步转移概率矩阵分别简记为()ij p n 和()n P . （3）初始分布、绝对分布称((0)),,==∈i p P X i i E 为离散参数马氏链{}(),0,1,2,=X n n 的初始分布，记为0P ，称()(){},,==∈j p n P X n j j E 为马尔可夫链{}0n X n ≥的绝对分布，记为P n . （4）离散参数齐次马氏链设{}(),0,1,2,=X n n 是一离散参数马氏链，如果其一步转移概率()ij p n 恒与起始时刻n 无关，记为ij p ，则称{}(),0,1,2,=X n n 为离散参数齐次马氏链。

若{}(),0,1,2,=X n n2是离散参数齐次马氏链，则其k 步转移概率记为(),i j p k ，一步转移概率矩阵和k 转移概率矩阵分别记为P 和().P k(5) 离散参数齐次马氏链的遍历性离散参数齐次马氏链{X (n ) ,n=0,1,2… }，若对一切状态i ，j ，存在与i 无关的极限()()lim 0,ij j n p n i j E →+∞=π>∈则称此马氏链具有遍历性.0,1j j j Ej E ππ∈>∈=∑若且则称{},j j E π∈为离散参数齐次马氏链{X (n ) ,n=0,1,2… }的极限分布，或称为最终分布，记为{},j j E ∏=∈π（6）离散参数齐次马氏链的平稳分布离散参数齐次马氏链{X (n ) ,n=0,1,2… }，若存在{v j , j ∈E } 满足条件：1)0,2)13)j jj Ej i iji Ev j E vv v p ∈∈≥∈==∑∑则称此马氏链是平稳的，称 { v j , j ∈E } 为此马氏链的平稳分布。

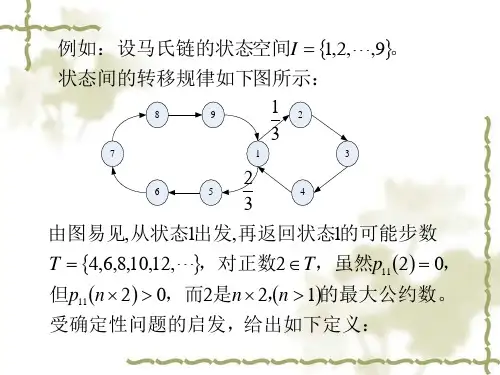
第四章 二阶矩过程、平稳过程和随机分析 习题解答1、 设∑=-=Nk k k kn U n X 1)cos(2ασ，其中k σ和k α为正常数，)2,0(~πU U k ，且相互独立，N k ,,2,1 =，试计算},1,0,{ ±=n X n 的均值函数和相关函数，并说明其是否是平稳过程。

解：计算均值函数和相关函数如下0)}{cos(2)cos(2}{)(11=-=⎭⎬⎫⎩⎨⎧-==∑∑==Nk k k k N k k k k n X U n E U n E X E n ασασμ∑∑∑∑∑∑======-=--=--=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎦⎤⎢⎣⎡-⋅⎥⎦⎤⎢⎣⎡-=Ni i i N i i i i i i Ni Nj j j i i j i N j j j j N i i i i X m n U m U n E U m U n E U m U n E m n R 12121111)](cos[)}cos(){cos(2)}cos(){cos(2)cos(2)cos(2),(ασαασαασσασασ因此可知，},1,0,{ ±=n X n 是平稳随机过程。

2、 设有随机过程))(cos()(t t A t X πηω+=，其中0>ω为常数，}0),({≥t t η是泊松过程，A 是与)(t η独立的随机变量，且2/1}1{}1{===-=A P A P 。

（1） 试画出此过程的样本函数，并问样本函数是否连续？ （2） 试求此过程的相关函数，并问该过程是否均方连续？ 解：（1）样本函数不连续。

（2）令：012≥>t t ，下面求相关函数：)(221)(212210)(1212211212121211212212122112221122121121212cos cos )]}(cos[)]({cos[21!)]([)]}(cos[)]({cos[)1(21))]}()(()(cos[))]()(()(2)({cos[21))]}()(()(cos[))]()(()({cos[21))}(cos())({cos(}{))}(cos())(cos({)}()({),(t t t t k t t k kX e t t e t t t t e k t t t t t t t t t t t t t t t E t t t t t t t t E t t t t E A E t t t t A E t X t X E t t R ----∞=--⋅=⋅-++=⋅-⋅-++-=-+-+-+++=-+-++++=++⋅=++==∑λλλωωωωλωωηηπωηηππηωηηπωηηπωπηωπηωπηωπηω因为：t t t R ωξ2cos ),(=因此该过程是均方连续的随机过程。

第四章习题解答4.1Y1,Y2,···是来自总体Y的随机变量，与X0独立，h(x,y)是实函数.对于n 1，取X n=h(X n−1,Y n).设{X n}的状态空间为I，验证{X n}是马氏链，给出转移概率p ij.解：由题知，Y k与X1,···,X k−1独立,k 1,∀n,i,j,i1,...,i n−1∈I有，P(X n+1=j|X n=i,X n−1=i n−1, (X0)i0)=P(h(i,Y n+1)=j|X n=i,X n−1=i n−1,···,X0=i0)=P(h(i,Y n+1)=j|X n=i)=P(h(i,Y)=j)=P(h(i,Y1)=j|X0=i)=P(X1=j|X0=i).∴X n是马氏链，P ij=P(h(i,Y)=j).4.2设{X i,i 0}是取非负整数值的独立同分布的随机变量序列，V ar(X0)>0.验证以下随机序列是马氏链：(a){X n,n 0};(b){S n,n 0}，其中S n=∑ni=0X i;(c){ξn,n 0}，其中ξn=∑ni=0(1+X i).解：∀n,i,j,i0,···,i n−1∈N+,(a).P(X n+1=j|X n=i,X n−1=i n−1,···,X0=i0)=P(X n+1=j)= P(X n+1=j|X n=i)=P(X1=j)=P(X1=j|X0=i).1第四章离散时间马尔可夫链第四章离散时间马尔可夫链(b).P(S n+1=j|S n=i,S n−1=i n−1,···,X0=i0)=P(X n+1=j−i|X n=i−i n−1,···,X0=i0)=P(X n+1=j−i)=P(X n+1=j−i,S n=i|S n=i)=P(S n+1=j|S n=i)=P(X1=j−i)=P(X1=j−i|X0=i)=P(S1=j|S0=i).(c).P(ξn+1=j|ξn=i,ξn−1=i n−1,···,ξ0=i0)=P(X n+1=ji −1)=P(X n+1=ji−1|ξn=i)=P(ξn+1=j|ξn=i)=P(X1=ji −1)=P(X1=ji−1|X0=i)=P(ξ1=j|ξ0=i).4.3马氏链的状态空间是I=(1,2,3,4,5)，转移概率矩阵P=0.20.80000.50.5000000.50.500.20.3000.500001界定马氏链的状态。

第四章 Markov 过程本章我们先讨论一类特殊的参数离散状态空间离散的随机过程，参数为0{0,1,2,}T N ==L ，状态空间为可列{1,2,}I =L 或有限{1,2,,}I n =L 的情况，即讨论的过程为Markov 链。

Markov 链最初由Markov 于1906年引入，至今它在自然科学、工程技术、生命科学及管理科学等诸多领域中都有广泛的应用。

之后我们将讨论另一类参数连续状态空间离散的随机过程，即纯不连续Markov 过程。

§4.1 Markov 链的定义与性质一、Markov 链的定义定义 4.1设随机序列{;0}n X n ≥的状态空间为I ，如果对0n N ∀∈，及0110011,,,,,{,,,}0n n n n i i i i I P X i X i X i +∈===>L L ，有：11001111{,,,}{}n n n n n n n n P X i X i X i X i P X i X i ++++=======L （4.1.0)则称{;0}n X n ≥为Markov 链。

注1：等式（4.1.0）刻画了Markov 链的特性，称此特性为Markov 性或无后效性，简称为马氏性。

Markov 链也称为马氏链。

定义4.2 设{;0}n X n ≥为马氏链，状态空间为I ，对于,i j I ∀∈，称1{}()ˆn n i j P X j X i p n +===为马氏链{;0}n X n ≥在n 时刻的一步转移概率。

注2：一步转移概率满足：()0,,()1,i j i jj Ip n i j Ipn i I ∈≥∈=∈∑若对于,i j I ∀∈，有1{}()ˆn n i j i j P X j X i p n p +===≡即上面式子的右边与时刻n 无关，则称此马氏链为齐次（或时齐的）马氏链。

设{}0()(0),p i P X i i I ==∈，如果对一切i I ∈都有00()0,()1i Ip i p i ∈≥=∑，称0()p i 为马氏链的初始分布。

随机过程习题解答第一章习题解答1．设随机变量X 服从几何分布，即：(),0,1,2,kP X k pqk ===。

求X 的特征函数，EX 及DX 。

其中01,1p q p <<=-是已知参数。

解()()jtxjtk k X k f t E ee pq ∞===∑ =()1jt k jtk pp qe qe ∞==-∑又200()kkk k q qE X kpq p kq p p p ∞∞======∑∑（其中 0(1)nnnn n n nx n x x ∞∞∞====+-∑∑∑）令 0()(1)nn S x n x ∞==+∑则 1000()(1)1xxnn k n xS t dt n t dt x x∞∞+===+==-∑∑⎰⎰同理 2(1)2kkkk k k k k kx k x kx x ∞∞∞∞=====+--∑∑∑∑令2()(1)kk S x k x ∞==+∑ 则211()(1)(1)xkk kk k k S t dt k t dt k xkx ∞∞∞+====+=+=∑∑∑⎰）2、（1） 求参数为(,)p b 的Γ分布的特征函数，其概率密度函数为（2） 其期望和方差；（3）证明对具有相同的参数的b 的Γ分布，关于参数p 具有可加性。

解 （1）设X 服从(,)p b Γ分布，则 （2）'1()(0)Xp E X fjb∴==（4）若(,)i i X p b Γ 1,2i = 则同理可得：()()i i P X b f t b jt∑=∑-3、设ln (),()(kZ F X E Zk =并求是常数）。

X 是一随机变量，()F x 是其分布函数，且是严格单调的，求以下随机变量的特征函数。

（1）(),(0,)Y aF X b a b =+≠是常数； （2）ln (),()(kZ F X E Z k =并求是常数）。

解（1）11{()}{()}[()]P F x y P x F y F F y y --<=<==（01y ≤≤） ∴00()0111y F y yy y <⎧⎪=≤≤⎨⎪>⎩∴()F x 在区间[0，1]上服从均匀分布()F x ∴的特征函数为11001()(1)jtx jtx jt X e f t e dx e jt jt ===-⎰ （2）ln ()()()[]jtz jt F x Z f t E e E e ===1ln 01jt ye dy ⋅⎰=111jty dy jt =+⎰4、设12n X X X ，，相互独立，且有相同的几何分布，试求1nkk X =∑的分布。

随机过程第三章与第四章习题解答3.1 解：令()N t 表示(0,)t 时间内的体检人数，则()N t 为参数为30的poisson 过程。

以小时为单位。

则((1))30E N =。

4030(30)((1)40)!k k P N e k -=≤=∑。

3.2 解：法一：（1）乘坐1、2路汽车所到来的人数分别为参数为1λ、2λ的poisson 过程，令它们为1()N t 、2()N t 。

1N T 表示1()N t =1N 的发生时刻，2N T 表示2()N t =2N 的发生时刻。

1111111111()exp()(1)!N NN T f t t t N λλ-=-- 2221222222()exp()(1)!N NN T f t t t N λλ-=--1212121221112,12|12211122212(,)(|)()exp()exp()(1)!(1)!N N N N N NNN N T T T T T f t t f t t f t t t t t N N λλλλ--==---- 12212121112211122210012()exp()exp()(1)!(1)!NNt N N N N P T T dt t t t t dt N N λλλλ∞--<=----⎰⎰（2）当1N =2N 、1λ=2λ时，12121()()2N N N N P T T P T T <=>=法二：（1）乘车到来的人数可以看作参数为1λ+2λ的泊松过程。

令1Z 、2Z 分别表示乘坐公共汽车1、2的相邻两乘客间到来的时间间隔。

则1Z 、2Z 分别服从参数为1λ、2λ的指数分布，现在来求当一个乘客乘坐1路汽车后，下一位乘客还是乘坐1路汽车的概率。

212211122210()exp()exp()z p P Z Z dz z z dz λλλλ∞=<=--⎰⎰112λλλ=+。

故当一个乘客乘坐1路汽车后，下一位乘客乘坐2路汽车的概率为1-p 212λλλ=+上面的概率可以理解为：在乘客到来的人数为强度1λ+2λ的泊松过程时，乘客分别以112λλλ+概率乘坐公共汽车1，以212λλλ+的概率乘坐公共汽车2。