随机过程第一章(下)
- 格式:pdf
- 大小:321.07 KB
- 文档页数:30

第一章概论第1题某公共汽车站停放两辆公共汽车A 和B ,从t=1秒开始,每隔1秒有一乘客到达车站。
如果每一乘客以概率21登上A 车,以概率21登上B 车,各乘客登哪一辆车是相互统计独立的,并用j ξ代表t=j 时乘客登上A 车的状态,即乘客登上A 车则j ξ=1,乘客登上B 车则jξ=0,则,21}0{,21}1{====j j P P ξξ当t =n 时在A 车上的乘客数为n n j j n ηξη,1∑==是一个二项式分布的计算过程。
(1)求n η的概率,即;,...,2,1,0?}{n k k P n ===η(2)当公共汽车A 上到达10个乘客时,A 即开车(例如t =21时921=η,且t =22时又有一个乘客乘A 车,则t =22时A 车出发),求A 车的出发时间n 的概率分布。
解(1):nn k n k P ⎟⎠⎞⎜⎝⎛⎟⎟⎠⎞⎜⎜⎝⎛==21}{η 解(2):nn n n P P ⎟⎠⎞⎜⎝⎛⎟⎟⎠⎞⎜⎜⎝⎛−=⎟⎠⎞⎜⎝⎛⎟⎠⎞⎜⎝⎛⎟⎟⎠⎞⎜⎜⎝⎛−==−2191212191A)10n 9A 1-n (}n A {1名乘客登上车时刻第名乘客;在有时刻,车在开车在时刻车第2题设有一采用脉宽调制以传递信息的简单通信系统。
脉冲的重复周期为T ,每一个周期传递一个值;脉冲宽度受到随机信息的调制,使每个脉冲的宽度均匀分布于(0,T )内,而且不同周期的脉宽是相互统计独立的随机变量;脉冲的幅度为常数A 。
也就是说,这个通信系统传送的信号为随机脉宽等幅度的周期信号,它是以随机过程)(t ξ。
图题1-2画出了它的样本函数。
试求)(t ξ的一维概率密度)(x f t ξ。
解:00(1)()()(){()}{()0}[(1),],(0,){()}{[(1),]}{[(1)]}1(1)(1)1({()0}1{()}t A A n n n Tt n T f x P x A P x P t A P P t P t n T nT n T P t A P t n T nT P t n T d TT t n T T nT t T t n Tt n T T t n P t P t A ξδδξξηξηηηξξ−−=−+====∈−∈==∈−+=>−−=−+−=−==−−−=−−−==−==∫是任意的脉冲宽度01)(1)()()()()(1)()t A T tn T Tf x P x A P x t t n x A n x T T ξδδδδ=−−∴=−+⎛⎞⎛⎞=−−+−−⎜⎟⎜⎟⎝⎠⎝⎠第3题设有一随机过程)(t ξ,它的样本函数为周期性的锯齿波。







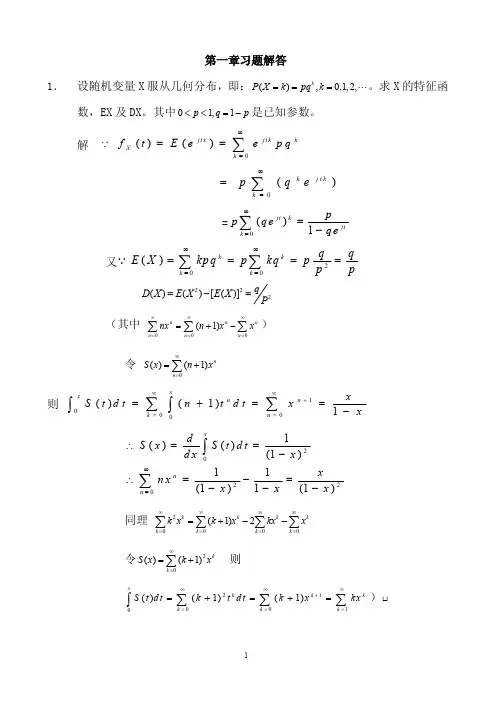


概率论与随机过程习题答案标准化工作室编码[XX968T-XX89628-XJ668-XT689N]《概率论与随机过程》第一章习题答案1. 写出下列随机试验的样本空间。
(1) 记录一个小班一次数学考试的平均分数(设以百分制记分)。
解: ⎭⎬⎫⎩⎨⎧⨯=n n nn S 100,,1,0 ,其中n 为小班人数。
(2) 同时掷三颗骰子,记录三颗骰子点数之和。
解:{}18,,4,3 =S 。
(3) 10只产品中有3只是次品,每次从其中取一只(取出后不放回),直到将3只次品都取出,记录抽取的次数。
解: {}10,,4,3 =S 。
(4) 生产产品直到得到10件正品,记录生产产品的总件数。
解: {} ,11,10=S 。
(5) 一个小组有A ,B ,C ,D ,E5个人,要选正副小组长各一人(一个人不能兼二个职务),观察选举的结果。
解: {}ED EC EB EA DE DC DB DA CE CD CB CA BE BD BC BA AE AD AC AB S ,,,,,,,,,,,,,,,,,,,=其中,AB 表示A 为正组长,B 为副组长,余类推。
(6) 甲乙二人下棋一局,观察棋赛的结果。
解: {}210,,e e e S =其中,0e 为和棋,1e 为甲胜,2e 为乙胜。
(7) 一口袋中有许多红色、白色、蓝色乒乓球,在其中任意取4只,观察它们具有哪几种颜色。
解: {}rwb wb rb rw b w r S ,,,,,,=其中,,,,b w r 分别表示红色、白色、蓝色。
(8) 对某工厂出厂的产品进行检查,合格的盖上“正品”,不合格的盖上“次品”,如连续查出二个次品就停止检查,或检查4个产品就停止检查,记录检查的结果。
解: {}1111,1110,1101,0111,1011,1010,1100,0110,0101,0100,100,00=S 其中,0为次品,1为正品。
(9) 有A ,B ,C 三只盒子,a ,b ,c 三只球,将三只球装入三只盒子中,使每只盒子装一只球,观察装球的情况。
1解:该试验的结果有9个:(0,a ),(0,b ),(0,c ),(1,a ),(1,b ),(1,c ),(2,a ),(2,b ),(2,c )。
所以,(1)试验的样本空间共有9个样本点。
(2)事件A 包含3个结果:不吸烟的身体健康者,少量吸烟的身体健康者,吸烟较多的身体健康者。
即A 所包含的样本点为(0,a ),(1,a ),(2,a )。
(3)事件B 包含3个结果:不吸烟的身体健康者,不吸烟的身体一般者,不吸烟的身体有病者。
即B 所包含的样本点为(0,a ),(0,b ),(0,c )。
2、解 (4)(1)ABBC AC 或ABC ABC ABC ABC ; (5)(2)ABBC AC (6)(提示:题目等价于A ,B ,C 至少有2个发生,与(1)相似); (7)(3)ABC ABC ABC ;(8)(4)AB C 或ABC ;(9)(提示:A ,B ,C 至少有一个发生,或者A B C ,,不同时发生);3(1)错。
依题得,但,故A 、B 可能相容。
(2)错。
举反例 (3)错。
举反例 (4)对。
证明:由,知,即A 和B 交非空,故A 和B 一()()()()0=-+=B A p B p A p AB p 空集≠B A ()6.0=A p ()7.0=B p ()()()()()3.03.1>-=-+=B A p B A p B p A p AB p定相容。
4、解(1)因为A B ,不相容,所以A B ,至少有一发生的概率为:()()()=0.3+0.6=0.9P A B P A P B =+(2) A B , 都不发生的概率为:()1()10.90.1P A B P A B =-=-= ;(3)A 不发生同时B 发生可表示为:AB ,又因为A B ,不相容,于是()()0.6P A B P B == ;5解:由题知,. 因得,故A,B,C 都不发生的概率为.6、解 设A ={“两次均为红球”},B ={“恰有1个红球”},C ={“第二次是红球”} 若是放回抽样,每次抽到红球的概率是:810,抽不到红球的概率是:210,则 (1)88()0.641010P A =⨯=; ()3.0=BC AC AB p ()05.0=ABC P ()()()()()ABC p BC p AC p AB p BC AC AB p 2-++= ()()()()4.023.0=+=++ABC p BC p AC p AB p ()()C B A p C B A p -=1()()()()()()()()[]ABC p BC p AC p AB p C p B p A p +++-++-=1()05.04.02.11+--=15.0=(2)88()210.321010P B =⨯⨯-=(); (3)由于每次抽样的样本空间一样,所以:8()0.810P C == 若是不放回抽样,则(1)2821028()45C P A C ==;(2)118221016()45C C P B C ==; (3)111187282104()5A A A A P C A +==。
随机过程习题解答第一章习题解答1.设随机变量X 服从几何分布,即:(),0,1,2,kP X k pqk ===。
求X 的特征函数,EX 及DX 。
其中01,1p q p <<=-是已知参数。
解()()jtxjtk k X k f t E ee pq ∞===∑ =()1jt k jtk pp qe qe ∞==-∑又200()kkk k q qE X kpq p kq p p p ∞∞======∑∑(其中 0(1)nnnn n n nx n x x ∞∞∞====+-∑∑∑)令 0()(1)nn S x n x ∞==+∑则 1000()(1)1xxnn k n xS t dt n t dt x x∞∞+===+==-∑∑⎰⎰同理 2(1)2kkkk k k k k kx k x kx x ∞∞∞∞=====+--∑∑∑∑令2()(1)kk S x k x ∞==+∑ 则211()(1)(1)xkk kk k k S t dt k t dt k xkx ∞∞∞+====+=+=∑∑∑⎰)2、(1) 求参数为(,)p b 的Γ分布的特征函数,其概率密度函数为(2) 其期望和方差;(3)证明对具有相同的参数的b 的Γ分布,关于参数p 具有可加性。
解 (1)设X 服从(,)p b Γ分布,则 (2)'1()(0)Xp E X fjb∴==(4)若(,)i i X p b Γ 1,2i = 则同理可得:()()i i P X b f t b jt∑=∑-3、设ln (),()(kZ F X E Zk =并求是常数)。
X 是一随机变量,()F x 是其分布函数,且是严格单调的,求以下随机变量的特征函数。
(1)(),(0,)Y aF X b a b =+≠是常数; (2)ln (),()(kZ F X E Z k =并求是常数)。
解(1)11{()}{()}[()]P F x y P x F y F F y y --<=<==(01y ≤≤) ∴00()0111y F y yy y <⎧⎪=≤≤⎨⎪>⎩∴()F x 在区间[0,1]上服从均匀分布()F x ∴的特征函数为11001()(1)jtx jtx jt X e f t e dx e jt jt ===-⎰ (2)ln ()()()[]jtz jt F x Z f t E e E e ===1ln 01jt ye dy ⋅⎰=111jty dy jt =+⎰4、设12n X X X ,,相互独立,且有相同的几何分布,试求1nkk X =∑的分布。
第四节 全概率公式与贝叶斯公式(续)定理 设事件组n B B B ,,,21⋅⋅⋅满足:(1)S B n i i =∑=1;(2)n B B B ,,,21⋅⋅⋅互不相容;(3)n i B P i ,,2,1,0)(⋅⋅⋅=>, (如果某0)(0=iB P ,则在概率计算中将其去掉) 则有如下结论(I)对任意事件A ,恒有 )|()()(1i ni i B A P B P A P ∑==; (1.10) (II)对任意事件)0)((>A P A ,有 ∑===n j jj i i i i B A P B P B A P B P A P AB P A B P 1)|()()|()()()()|( ,n i ,,2,1⋅⋅⋅=,(1.11)注:这两个公式当+∞=n 时,(条件也变为可列个事件),也有相应的公式.)|()()(1i i i B A P B P A P ∑+∞== , ∑∞+===1)|()()|()()()()|(j jj i i i i B A P B P B A P B P A P AB P A B P .1. 理论意义,以后经常在论证推导中用到;2. 实际计算概率方法,化难为易,解决问题;3. 注意典型例题及在变化的情景中灵活运用;4. 贝叶斯公式在概率诊断,概率推断方面有用。
例 4 在无线电通讯中,由于随机干扰,当发出信号为“0”时,收到信号为“0”、不清和1的概率分别为0.7,0.2,0.1; 当发出信号为 1时,收到信号为1、不清和0的概率分别为0.9,0.1和0.如果在发报过程中0和1出现的概率分别是0.6和0.4,当收到信号不清时,原发信号是什么?试加以推测. 解 设=1B 原发信号为“0”, =2B 原发信号为“1”, =A 收到信号“不清”,由贝叶斯公式得)|()()|()()|()()|(2211111B A P B P B A P B P B A P B P A B P +=75.01.04.02.06.02.06.0=⨯+⨯⨯=, )|()()|()()|()()|(2211222B A P B P B A P B P B A P B P A B P +=25.01.04.02.06.01.04.0=⨯+⨯⨯= . 由于收到信号不清时, 原发信号为“0”概率较之原发信号为“1”的概率为大,因此通常应推断原发信号为“0”.例5 甲袋中装有3只红球、2只白球,乙袋中装有红、白球各2只.从甲袋中任取2只球放入乙袋,然后再从乙袋中任意取出3只球.(1) 求从乙袋中至多取出1只红球的概率;(2) 若从乙袋中取出的红球不多于1只,求从甲袋中取出的2只全是白球的概率.解 令=A 从乙袋中至多取出1只红球, =i B 从甲袋中恰好取出i 只红球, (i -2只白球), 2,1,0=i ;(1) 易知210,,B B B 互不相容,S B B B =++210 ,且⎪⎪⎪⎩⎪⎪⎪⎨⎧=====-2,1031,1060,101)(25223i i i C C C B P i i i ; 又⎪⎪⎪⎩⎪⎪⎪⎨⎧====+=-+-+2,511,210,54)|(3624123402i i i C C C C C B A P i i ii i , 故由全概率公式得)|)(()(2i i i B A B P A P ∑== 2511511032110654101=⨯+⨯+⨯=; (2) 易知要求概率)|(0A B P ,由贝叶斯公式得112251154101)()|()()|(000=⨯==A P B A P B P A B P .第五节 事件的独立性一般情况下,条件概率)()()()|(A P B P AB P B A P ≠=, 这说明事件B 的发生对于事件A 发生的概率有影响.如果事件B 的发生不影响事件A 发生的概率, 即)()()()|(A P B P AB P B A P ==,便得 )()()(B P A P AB P =.我们把具有这种性质的两个事件A 与B 称为是相互独立的,即有定义8 对任意两个事件A 、B ,若成立 )()()(B P A P AB P =, 则称A 与B 相互独立,简称独立.例 把一颗匀称的骰子连续掷两次,观察出现的点数。
第一章随机变量基础1 历史上哪些学者对随机过程学科的基础理论做出了突出贡献?答: 随机过程整个学科的理论基础是由柯尔莫哥洛夫和杜布奠定的。
这一学科最早源于对物理学的研究,如吉布斯、玻尔兹曼、庞加莱等人对统计力学的研究,及后来爱因斯坦、维纳、莱维等人对布朗运动的开创性工作。
1907 年前后,马尔可夫研究了一系列有特定相依性的随机变量,后人称之为马尔可夫链。
1923 年维纳给出布朗运动的数学定义,直到今日这一过程仍是重要的研究课题。
随机过程一般理论的研究通常认为开始于20 世纪30 年代。
1931 年,柯尔莫哥洛夫发表了《概率论的解析方法》,1934 年A·辛饮发表了《平稳过程的相关理论》,这两篇著作奠定了马尔可夫过程与平稳过程的理论基础。
1953 年,杜布出版了名著《随机过程论》,系统且严格地叙述了随机过程基本理论。
2 全概率公式的含义?答:全概率公式的含义就是各种可能发生的情况的概率之和为1。
3 概率空间有哪几个要素,其概念体现了对随机信号什么样的建模思想?答:样本空间、事件集合、概率函数称为概率空间的三要素。
概率函数建立了随机事件与可描述随机事件可能性大小的实数间的对应关系,因此,概率空间是在观测者观测前对随机事件发生的可能性大小进行了量化,其有效性是通过多次观测体现出来的,也即在多次观测中,某个随机事件发生的频率可直接认为与其发生的概率相等,所以,概率空间的建模思想实际是对大量观测中某随机事件发生频率的稳定性的描述。
4 可用哪些概率函数完全描述一个随机变量?答:概率分布函数(cdf)、概率密度函数(pdf )、特征函数(cf)、概率生成函数(gf)。
5 可用哪些数字特征部分描述一个随机变量?答:均值、方差、协方差、相关系数和高阶矩。
6 随机变量与通常意义上的变量有何区别与联系?答:随机变量具有通常意义上的变量的所有性质和特征(即变量特性),还增加了变量取每个值的可能性大小的描述(即概率特性)。
第一章一. 填空题1.p(A)=0.5,p(B)=0.7,A与B相互独立,则p(AUB)= _2.若已知两点(x1,y 1),(x2,y2)有x1 < x2, y 1<y2,则概率密度p{ x1<x< x2, y 1< y < y2}=__.3.若p(A)=0.2,p(B)=0.5,p(C)=0.1,且p(A),p(B),p(C)两两相互独立,则p A(C|B)=__.4.设X,Y是相互独立的随机变量,已知EX=1 ,EY=2,DX=1 ,DY=2 则E(XY)=___,E(2X+3Y) =___, D(2X+3Y) =__.5.若X1,X2,…,X n是相互独立的随机变量,且g i(t)是X i的特征函数,i=1,2,…,n)则X=X1+X2+…X n的特征函数g(t)=__.二.证明题1.设P(S)是的母函数,试证:(1)若E(X)存在,则EX=P′(1)(2)若D(X)存在,则 DX = P"(1)+ P′(1)-[ P′(1)]22.试证明连续型随机变量的全概率公式:p(A)=dF Y(y)=f Y(y)dy三.计算题1. 通过抛掷一枚均匀硬币定义一个随机过程{X(t),-∞< t<∞},其中X(t)=试求随机过程X(t)的一维分布函数F(x;-).2.设X服从B(n,p),求X的特征函数g(t).3. 设商店在一天的顾客数N服从[900,1100]上的均匀分布,又设每位顾客所花的钱Xi服从N(100,502);求商店的日销售额Z的平均值.4. 已知随机变量X服从[0,a]上的均匀分布,且随机变量Y服从[X,a]上的均匀分布,试求:(1)E(Y|X=a),0x a (2)E(Y)参考答案一.填空题 1. 0.852. F(x 2,y 2)-F(x 1,y 2)-F(x 2,y 1)+F(x 1,y 1)3. 0.14. 2, 8, 225. g 1(t) g 2(t)…g n (t) 二.证明题1. 证明:(1)因为p (s )=s p kk k ∑∞=0,则p ′(s )=s kp k k k 11-∞=∑,令s↑1,得EX==∑∞=1k k kp p ′(1)。
第一章随机过程的概念与基本类型随机过程的定义和统计描述随机过程分布律和数字特征复随机过程随机过程基本类型随机变量在每次试验的结果中,以一定的概率取某个事先未知,但为确定的数值。
在实际应用中,我们经常要涉及到在试验过程中随时间t而改变的随机变量。
例如,接收机的噪声电压,此外,还包括生物群体的增长问题;电话交换机在一定时间段内的呼叫次数;一定时期内的天气预报;固定点处海平面的垂直振动;等等在第W i 次试验中测量获得的噪声电压X t 是一个样本函数)(1t X w =)(2t X w =)(3t X w =)(t X kw =)(t X n w =1t 2t定义2.1设(Ω,F,P)是概率空间,T是给定的参数集,若对每个t∈T,由一个随机变量X(t,e)与之对应,则称随机变量族{X(t,e),t∈T}是(Ω,F,P)上的随机过程。
随机过程{X(t,e),t∈T}可以认为是一个二元函数。
对固定的t,X(t,e)是(Ω,F,P)上的随机变量;对固定的e,X(t,e)是是随机过程{X(t,e),t∈T}的一个样本函数。
X(t)通常表示为在时刻t所处的状态。
X(t)的所有可能状态所构成的集合称为状态空间或相空间。
通常我们可以根据随机变量X(t)在时间和状态上的类型区分随机过程的类型。
在时间和状态上都连续连续型随机过程在时间上连续,离散型随机过程状态上离散在时间上离散,连续型随机序列状态上连续在时间上离散,离散型随机序列状态上离散有限个随机变量统计规律联合分布函数随机过程统计规律有限维分布函数族设X T ={X(t),t ∈T}是随机过程,对任意n ≥1和t 1,t 2, …,t n ∈T ,随机向量(X(t 1),X(t 2), …,X(t n ))的联合分布函数为})(,)({),,,(1121,,1n n n t t x t X x t X P x x x F n ≤≤=L L L 这些分布函数的全体}1,,,,),,,({2121,1≥∈=n T t t t x x x F F n n t t n L L L 称为X T ={X t ,t ∈T}的有限维分布函数。
有限维分布函数的性质对称性对于{t 1,t 2, …,t n }的任意排列},,,{21n i i i t t t L ),,(),,,(111,,21,,ni i n i in t t t t n t t x x F x x x F L L L L =相容性当m<n 时,),,,,,,(),,,(21,,,,21,,11∞∞=L L L L L L m t t t m t t x x x F x x x F n m m对称性有限维分布函数族相容性Kolmogorov存在定理设已给参数集T及满足对称性和相容性条件的分布函数族F,则必存在概率空间(Ω,F,P)及定义在其上的随机过程{X(t),t∈T},它的有限维分布函数族是F。
设X T ={X(t),t ∈T}是随机过程,如果对任意t ∈T ,EX(t)存在,则称函数Tt t EX t m def x ∈=),()(为X T 的均值函数,反映随机过程在时刻t 的平均值。
若对任意t ∈T ,E(X(t))2存在,则称X T 为二阶矩过程,而称Tt s t m t X s m s X E t s B X X def X ∈−−=,)}],()()}{()([{),(为X T 的协方差函数,反映随机过程在时刻t 和s 时的线性相关程度。
[]Tt t m t X E t t B t D X X X ∈−==,)()(),()(2为X T 的方差函数,反映随机过程在时刻t 对均值的偏离程度。
Tt s t X s X E t s R X ∈=,)],()([),(为X T 的相关函数,反映随机过程在时刻t 和s 时的线性相关程度。
数字特征对于二阶矩随机过程,其协方差函数和相关函数一定存在,且有如下关系:)()(),(),(t m s m t s R t s B X X X X −=例题2.5设随机过程0),sin()cos()(>+=t t Z t Y t X θθ其中,Y 和Z 是相互独立的随机变量,且EY=EZ =0,DY=DZ=σ2,求X(t)的均值函数和协方差函数。
例题2.6设随机过程X(t)=Y+Zt ,t>0,其中Y,Z 是相互独立的N(0,1)随机变量,求{X(t),t>0}的一、二维概率密度族。
两个随机过程之间的关系互协方差函数互相关函数定义:设{X(t),t ∈T},{Y(t), t ∈T}是两个二阶矩过程,则称T t s t m t Y s m s X E t s B Y X XY ∈−−=,))],()())(()([(ˆ),(为{X(t),t ∈T}与{Y(t), t ∈T}的互协方差函数,称)]()([ˆ),(t Y s X E t s R XY =为{X(t),t ∈T}与{Y(t), t ∈T}的互相关函数。
两个随机过程{X(t),t ∈T}与{Y(t), t ∈T}的互不相关定义),(=t s B XY 互协方差函数与互相关函数之间的关系)()(),(),(t m s m t s R t s B Y X XY XY −=例题2.8:设X(t)为信号过程,Y(t)为噪声过程,令W(t)=X(t)+Y(t),求W(t)的均值函数和相关函数。
例题2.7设有两个随机过程X(t)=g 1(t+ε)和Y(t)=g 2(t+ε),其中g 1(t)和g 2(t)都是周期为L 的周期方波,ε是在(0,L)上服从均匀分布的随机变量,求互相关函数R XY (t,t+τ)的表达式。
复随机过程定义:设{Xt , t∈T},{Yt, t∈T}是取实数值的两个随机过程,若对任意t∈TtttiYXZ+=其中,则称{Zt , t∈T}为复随机过程。
1−=i复随机过程的数字特征函数均值函数方差函数相关函数协方差函数tttZiEYEXZEtm+==)()(]))(())([(]|)([|)(2−−−−−−−−−−−−−−=−=tmZtmZEtmZEtD ZtZtZtZ][),(tsZZZEtsR=]))(())([(),(−−−−−−−−−−−−−−=tmZsmZEtsB ZtZsZ−−−−−−−=)()(),(),(tmsmtsRtsB ZZZZ相互之间的关系复随机过程的性质复随机过程{XT,,t∈T}的协方差函数B(s,t)具有性质:(1)对称性,(2)非负定性,对任意ti ∈T及复数ai,i=1,2, …,n,n≥1,有−−−−−−=),(),(s tBt sB∑=≥nj ijijiaattB1,),(证明两个复随机过程{X t },{Y t }的互相关函数定义为)(),(t s XY Y X E t s R =互协方差函数定义为−−−−−−−−−−−−−−=)]([)]([),(t m Y s m X E t s B Y t X s XY 例题2.9设随机过程,其中X 1,X 2, …,X n 是相互独立的,且服从N(0,σk 2)的随机变量,w 1,w 2, …,w n 是常数,求{Z t ,t ≥0}的均值函数m(t)和相关函数R(s,t)。
0,1≥=∑=t e X Z n k t i k t k ϖ随机过程的几种基本类型1.正交增量过程2.独立增量过程3.马尔可夫过程4.正态过程5.维纳过程6.平稳过程定义:设{X(t),t ∈T}是零均值的二阶矩过程,若对任意的t 1<t 2≤t 3<t 4 ∈T ,有]))()(())()([(3412=−−−−−−−−−−−−−−−−−t X t X t X t X E 则称X(t)是正交增量过程。
例题设{X(t),t ∈T}是正交增量过程,T=[a,b]为有限区间,且规定X(a)=0,当a<s<t<b 时,求其协方差函数。
正交增量过程定义:设{X(t),t ∈T}是随机过程,若对任意的正整数n 和t 1<t 2<…<t n ∈T ,随机变量X(t 2)-X(t 1),X(t 3)-X(t 2), …,X(t n )-X(t n-1)是互相独立的,则称{X(t),t ∈T}是独立增量过程。
特点:独立增量过程在任一个时间间隔上过程状态的改变,不影响任一个与它不相重叠的时间间隔上状态的改变。
独立增量过程正交增量过程独立增量过程定义依据:不相重叠的时间区间上增量的统计相依性互不相关相互独立正交增量过程独立增量过程×正交增量过程独立增量过程二阶矩存在,均值函数恒为零平稳独立增量过程定义:设{X(t),t∈T}是独立增量过程,若对任意s<t,随机变量X(t)-X(s)的分布仅依赖于t-s,则称{X(t),t∈T}是平稳独立增量过程。
例题2.10考虑一种设备一直使用到损坏为止,然后换上同类型的设备。
假设设备的使用寿命是随机变量,令N(t)为在时间段[0,t]内更换设备的件数,通常可以认为{N(t),t≥0}是平稳独立增量过程。
定义:设{X(t),t ∈T}是随机过程,若对任意正整数n 及t 1<t 2, …<t n ,P(X(t 1)=x 1, …,X(t n-1)=x n-1)>0,且其条件分布})(|)({})(,,)(|)({111111−−−−=≤===≤n n n n n n n n x t X x t X P x t X x t X x t X P L 则称{X(t),t ∈T}是马尔可夫过程。
马尔可夫性系统在已知现在所处状态的条件下,它将来所处的状态与过去所处的状态无关。
马尔可夫过程定义:设{X(t),t ∈T}是随机过程,若对任意正整数n 及t 1,t 2, …,t n ∈T ,(X(t 1),X(t 2), …,X(t n ))是n 维正态随机变量,则称{X(t),t ∈T}是正态过程或高斯过程。
特点:1.在通信中应用广泛;2.正态过程只要知道其均值函数和协方差函数,即可确定其有限维分布。
正态过程定义:设{W(t),-∞<t< ∞}为随机过程,如果1.W(0)=0;2.它是独立、平稳增量过程;3.对任意s,t ,增量W(t)-W(s)~N(0,σ2|t-s|),σ2>0则称{W(t),-∞<t< ∞}为维纳过程,也称布朗运动过程。
定理:设{W(t),-∞<t< ∞}是参数为σ2的维纳过程,则1.对任意t ∈(-∞, ∞),W(t)~ N(0,σ2|t|);2.对任意-∞<a< s,t< ∞,),min()}]()()}{()([{2a t a s a W t W a W s W E −−=−−σ证明维纳过程维纳过程是正态过程的一种特殊形式定义:设{X(t),t ∈T}是随机过程,如果对任意常数τ和正整数n,t 1,t 2, …,t n ∈T ,t 1+τ,t 2+τ, …,t n +τ∈T ,(X(t 1),X(t 2), …,X(t n ))与(X(t 1+τ),X(t 2+τ), …,X(t n +τ))有相同的联合分布,则称{X(t),t ∈T}为严平稳过程或侠义平稳过程。