第1章 随机过程的基本概念

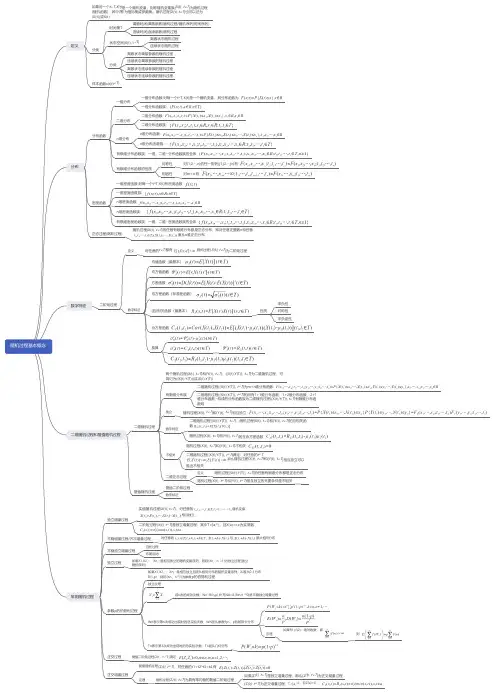
随机过程的基本概念和分类随机过程是一种随时间和其他随机变量而变化的数学对象，是概率论和统计学中的重要概念。

它被广泛应用于自然科学、工程学、经济学、金融学和社会科学等领域。

本文将介绍随机过程的基本概念和分类，帮助读者更好地理解随机过程的本质和应用。

1. 随机过程的基本概念随机过程是由一组随机变量组成的序列或函数，它表示在一定随机环境下某个系统或现象的发展过程。

在随机过程中，时间通常是一个自变量，而随机变量则是随时间变化的函数或序列。

根据定义域的不同，随机过程可以分为离散时间和连续时间两种类型。

离散时间的随机过程是在离散时间点上的序列，例如投骰子的过程。

连续时间的随机过程是在连续时间上的函数，例如天气的变化。

在通常情况下，连续时间的随机过程被认为是一个时间的连续函数，而离散时间的随机过程则表示为时间的离散序列。

随机过程可以用概率分布函数来表达。

对于连续时间的随机过程，它的概率分布函数是一个满足概率公理的函数。

对于离散时间的随机过程，概率分布可以用概率质量函数来描述。

概率分布函数可以通过研究随机过程的瞬时状态来推导。

随机过程的瞬时状态指位置和方向的一切资料，包括当前位置、速度和加速度等。

2. 随机过程的分类随机过程可以按照多种方式进行分类。

以下是一些常见的分类方式。

2.1 马尔可夫过程马尔可夫过程是一种随机过程，它的状态转移只与它的当前状态有关，而与过去状态和未来状态无关。

马尔可夫过程被广泛应用于物理、经济、金融和信号处理等领域。

根据定义域的不同，马尔可夫过程可以分为离散时间和连续时间两种类型。

离散时间的马尔可夫过程可以用转移矩阵来描述，而连续时间的马尔可夫过程则可以用转移概率密度函数来描述。

2.2 平稳过程平稳过程是指在不同时间段内，随机过程的统计分布不随时间而改变的随机过程。

这意味着它的瞬时状态空间必须一致，并且在不同的时间点上具有相同的概率分布。

平稳过程的例子包括白噪声、布朗运动和马尔可夫过程等。

第一章 随机过程的基本概念一、随机过程的定义例1：医院登记新生儿性别，0表示男,1表示女，X n 表示第n 次登记的数字，得到一个序列X 1 ， X 2 ， ···，记为｛X n ，n=1，2， ···}，则X n 是随机变量，而{X n ，n=1,2， ···｝是随机过程。

例2：在地震预报中，若每半年统计一次发生在某区域的地震的最大震级。

令X n 表示第n 次统计所得的值，则X n 是随机变量.为了预测该区域未来地震的强度，我们就要研究随机过程{X n ，n=1,2， ···｝的统计规律性。

例3：一个醉汉在路上行走，以概率p 前进一步，以概率1—p 后退一步（假设步长相同）。

以X(t)记他t 时刻在路上的位置，则｛X(t)， t ≥0｝就是（直线上的）随机游动。

例4：乘客到火车站买票,当所有售票窗口都在忙碌时,来到的乘客就要排队等候.乘客的到来和每个乘客所需的服务时间都是随机的，所以如果用X （t ）表示t 时刻的队长，用Y(t ）表示t 时刻到来的顾客所需等待的时间，则{X(t)， t ∈T ｝和｛Y(t)， t ∈T ｝都是随机过程。

定义：设给定参数集合T ，若对每个t ∈T, X （t ）是概率空间),,(P ℑΩ上的随机变量，则称{X(t ）， t ∈T}为随机过程，其中T 为指标集或参数集。

E X t →Ω:)(ω，E 称为状态空间，即X(t ）的所有可能状态构成的集合。

例1:E 为{0,1} 例2:E 为［0, 10]例3：E 为},2,2,1,1,0{ -- 例4：E 都为),0[∞+注：(1）根据状态空间E 的不同,过程可分为连续状态和离散状态,例1，例3为离散状态，其他为连续状态。

（2）参数集T 通常代表时间，当T 取R, R +, [a ，b]时,称｛X(t), t ∈T ｝为连续参数的随机过程；当T 取Z ， Z +时,称{X （t)， t ∈T}为离散参数的随机过程。

简述随机过程的基本概念随机过程是概率论的一个重要分支，研究随时间变化的随机现象。

它描述的是随机变量随时间的变动规律，并通过概率论的方法研究其统计特性。

随机变量是随机过程的基本组成部分，表示在给定的实验空间中，某一随机事件所对应的数值。

随机变量可以是离散的（比如抛硬币的正反面），也可以是连续的（比如投掷骰子的点数）。

随机过程可分为离散时间随机过程和连续时间随机过程两种类型。

离散时间随机过程是指在离散的时间点上进行观测，比如某一事件在每个小时的发生概率。

离散时间随机过程通常用随机序列来描述，其中每个随机序列代表不同的事件。

连续时间随机过程是指在连续的时间段内进行观测，比如某一事件在每个时间段内的发生概率。

连续时间随机过程可以通过概率密度函数来描述。

随机过程有两个重要的性质：平稳性和马尔可夫性。

平稳性是指随机过程的统计特性在时间上保持不变。

强平稳性要求整个随机过程的概率分布在时间上保持不变，弱平稳性只要求随机过程的均值和自相关函数在时间上保持不变。

马尔可夫性是指在给定过去的条件下，未来的状态只与当前状态有关。

这意味着给定当前的状态，过去的状态对于预测未来的状态是无关的。

随机过程可以通过随机过程的定义、概率密度函数、特征函数等进行建模和描述。

常用的随机过程模型包括泊松过程、马尔可夫链、布朗运动等。

泊松过程是离散时间且符合强平稳性和马尔可夫性的随机过程。

泊松过程描述了在一段时间内随机事件发生的次数，常用于描述到达某个服务中心或系统的流量。

马尔可夫链是具有马尔可夫性的随机过程。

在马尔可夫链中，系统的状态在不同的时间段内转移，且转移的概率只与当前的状态有关。

这种随机过程常用于描述具有一定变化规律的系统，如天气系统、金融市场等。

布朗运动是连续时间且连续状态的随机过程，它具有良好的连续性和马尔可夫性质。

布朗运动常用于建模和描述股票价格、汇率波动等金融领域中的随机变动。

随机过程的研究可以用于预测和分析各种现实生活中的随机变化。

随机过程的基本概念与应用随机过程是概率论中研究一系列随机事件在时间上的演化规律的重要分支。

它在各个领域都有着广泛的应用，在通信、控制、金融、生物、物理等方面都发挥着重要作用。

一、随机过程的基本概念1.1 随机过程的定义随机过程是指一组随机变量${X_t}$，其中$t$表示时间，$X_t$表示在时间$t$时刻随机变量的取值。

随机过程是随机变量的函数族，常用记号为${X_t:t\in T}$。

其中$t$取遍$T$所表示的时间集合，$T$可以是实数集、整数集或其他有限或无限集合。

1.2 随机过程的分类随机过程根据其时间变化的连续性与离散性可以分为连续时间随机过程和离散时间随机过程两种。

连续时间随机过程是指随机变量在时间上是连续的，如布朗运动、泊松过程等。

离散时间随机过程是指随机变量在时间上是离散的，如马尔可夫过程、随机游走等。

1.3 随机过程的性质随机过程具有多种性质，包括平稳性、独立性、齐次性等。

其中比较重要的平稳性是指在时间平移下，随机过程的统计性质保持不变，即一个随机过程是平稳的，当且仅当对于任意$t_1,t_2$，其一阶矩和二阶矩不随时间变化而改变。

例如，设随机过程${X_t:t\geq 0}$的均值为$\mu$，方差为$\sigma^2$，则其平稳性条件为：$$\mathbb{E}[X_t]=\mu, \ \forall t\geq 0$$$$\mathbb{E}[(X_s-\mu)(X_t-\mu)]=\sigma^2, \ \forall s,t\geq 0$$二、随机过程的应用随机过程在许多领域中都有着广泛的应用。

以下列举其中几个典型应用。

2.1 通信领域随机过程在通信领域中是必不可少的工具。

通信信号可以看作是一种随时间变化的随机过程，而信道则可看作是一种将输入信号映射成输出信号的随机过程。

因此，随机过程在信号调制、信噪比估计、编码等方面都有着广泛的应用。

2.2 控制领域在控制领域中，随机过程被广泛用于表示、建模和分析控制系统的动态特性。