频数分布直方表格式

数据统计中的频数分布及直方绘制数据统计是一项重要的工作，用于收集、处理、分析和解释数据以了解某个特定现象或问题。

其中，频数分布及直方图是常用的数据可视化方式，可帮助我们更直观地理解数据的分布情况。

本文将介绍频数分布的概念和计算方法，并详细说明如何使用直方图进行数据可视化。

一、频数分布频数是指某个特定数值在样本或总体中出现的次数。

频数分布是将数据按照数值的大小排列，并将每个数值出现的次数记录下来的表格或图形。

例如，假设我们有一个样本包含100个人的体重数据，将数据按照数值大小排序如下：56, 57, 58, 59, 59, 60, 60, 61, 62, 63, 63, 63, 64, 65, 66, 67, 67, 67, 68, 68, 69, 70, 70, 70, 70, 71, 71, 72, 72, ...我们可以通过统计每个数值出现的次数，得到频数分布表如下：体重频数56 157 158 159 260 261 162 163 364 165 166 267 368 269 170 471 272 2... ...通过频数分布表，我们可以看出每个体重数值出现的次数，进而掌握数据的分布情况。

然而，频数分布表的信息量相对有限，为了更直观地展示数据分布，我们可以使用直方图。

二、直方图绘制直方图是以矩形的高度来表示频数分布的图形。

其中，横轴表示数据的范围或组别，纵轴表示各个范围或组别对应的频数。

绘制直方图的步骤如下：1. 将数据按照大小顺序排列。

2. 将整个数据范围划分为若干个相等的组别（也称为“组距”），每个组别包含一定的数据范围。

组距的选择应根据数据的分布情况和样本大小来决定。

3. 统计每个组别中的频数，得到频数分布表。

4. 在纵轴上标注频数，横轴上标注组别。

5. 依次绘制每个组别的矩形，矩形的高度对应于该组别的频数。

下面以具体示例来说明如何绘制直方图。

假设我们有一个班级的学生成绩数据如下：65, 72, 80, 72, 76, 90, 88, 81, 75, 78, 70, 68, 73, 84, 87, 92, 75, 72, 78, 70首先，按照大小顺序排列数据，得到：65, 68, 70, 70, 72, 72, 72, 73, 75, 75, 76, 78, 78, 80, 81, 84, 87, 88, 90, 92接下来，选择组距为10，将数据范围划分为以下组别：60-69, 70-79, 80-89, 90-99统计每个组别中的频数，得到频数分布表：组别频数60-69 270-79 780-89 590-99 3然后，在纵轴上标注频数，在横轴上标注组别，绘制矩形并填充颜色，得到直方图。

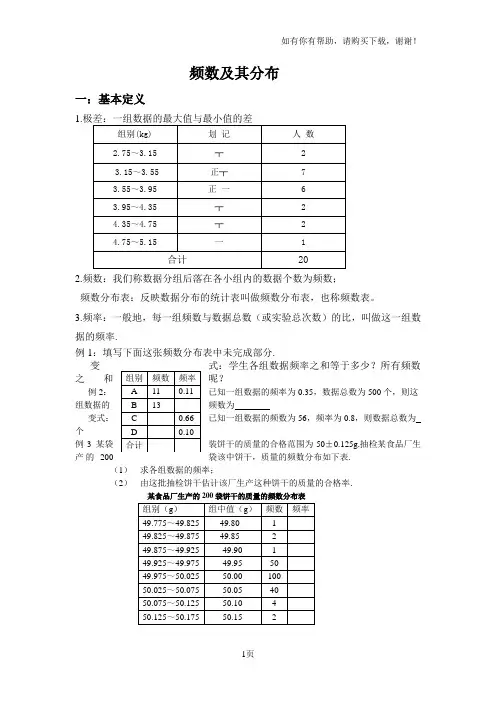
频数及其分布一：基本定义1.2.频数：我们称数据分组后落在各小组内的数据个数为频数；频数分布表：反映数据分布的统计表叫做频数分布表，也称频数表。

3.频率：一般地，每一组频数与数据总数（或实验总次数）的比，叫做这一组数据的频率.例1：填写下面这张频数分布表中未完成部分.变式：学生各组数据频率之和等于多少？所有频数Array之和呢？例2：已知一组数据的频率为0.35，数据总数为500个，则这组数据的频数为变式：已知一组数据的频数为56，频率为0.8，则数据总数为个例3 某袋装饼干的质量的合格范围为50±0.125g.抽检某食品厂生产的200袋该中饼干，质量的频数分布如下表.（1）求各组数据的频率；（2）由这批抽检饼干估计该厂生产这种饼干的质量的合格率.某食品厂生产的200袋饼干的质量的频数分布表二：频数分布直方图一：用来表示频数分布的基本统计图叫做频数分布直方图，简称直方图(Mstogram)．在统计数据时，按照频数分布表，在平面直角坐标系中，横轴标出每个组的端点，纵轴表示频数，每个矩形的高代表对应的频数，我们称这样的统计图为频数分布直方图，如图12-5所示，直方图中各矩形之间没有空隙.【说明】在画频数分布直方图时，首先要列出频数分布表.在分组时要注意：（1）组数适当；（2）组距相等.同时，分组要遵循三个原则：（1）不空，即该组必须有数据；（2）不重，即一个数据只能在一个组中；（3）不漏，即不能漏掉某一个数据.思考：频数分布直方图与条形统计图的区别？（1）条形统计图中，横轴上的数据是孤立的，是一个具体的数据。

而直方图中，横轴上的数据是连续的，是一个范围。

（2）条形统计图中，各个数据之间是相对独立的，各个条形之间是有空隙的。

而在直方图中，各长方形对应的是一个范围，由于每两个相邻范围之间不重叠、不遗漏，因此在直方图中，长方形之间没有空隙。

例．请观察图，并回答下面的问题：(1)被检测的矿泉水总数有多少种?(2)被检测矿泉水的最低pH为多少?(3)组界为6.9~7.3这一组的频数、频率分别是多少(每一组包括前一个边界值，不包括后一个边界值)?(4)根据我国2001年公布的生活饮用水卫生规范，饮用水的pH应在6.5—8.5的范围内．被检测的矿泉水不符合这一标准的有多少种?占总数的百分之几?思考：图中的频数分布直方图的每一组的边界值为多少？A．10.5 B．14.5 C．12.5 D．8.5三：拆线统计图及其特点折线统计图是用一个单位长度表示一定的数量，根据数量的多少描出各点，然后用线段顺次把各点连接起来.它既可以表示出项目的具体数量，又能清楚地反映事物变化的情况.折线统计图的特点：易于显示数据的变化趋势，如图12-4所示.例．超速行驶是交通事故频发的主要原因之一．交警部门统计某日7：00～9：00经过高速公路某测速点的汽车的速度，得到如下频数分布折线图（1）这一天7：00～9：00经过该观察点的车辆总数是多少（2）数据分组的组距是多少（3）若该路段汽车限速为110km/h，请问超速行驶的汽车有多少辆？占总数的百分之几（4）简单描述折线的波动情况，并说明它所表示的实际意义四：扇形统计图用圆代表总体，圆中的各个扇形分别代表总体中的不同部分，扇形的大小反映部分占总体的百分比的大小，这样的统计图叫做扇形统计图.扇形统计图主要是反映具体问题中的部分与整体的数量关系.扇形统计图的各部分占总体的百分比之和为100%或1，如图12-2所示.例1 如图12-6所示的是扇形统计图，求扇形B占总体的百分比.例每人捐书的册数/册 5 10 15 20相应的捐书人数/人17 22 4 2（1）该班的学生共多少名？（2）全班一共捐了多少册书？（3）若该班所捐图书按图12-7所示的比例分，则送给山区学校的书比送给本市兄弟学校的书多多少册？总结：条形统计图显示每组中的具体数据；扇形图显示部分在总体中占的百分比；频数直方图显示数据的分布情况；折线图显示数据的变化趋势综合练习：1 为了了解小学生的体能情况，抽取了某小学同年级学生进行跳绳测试，将所得数据整理后，画出如图12-11所示的频率分布直方图，已知图中从左到右前三个小组的频率分别是0.1，0.3，0.4，第一小组的频数为5，则第四小组的频率是，参加这次测试的学生有人.2某班同学参加环保知识竞赛，将学生的成绩（得分取整数）进行整理后分成五组，绘制成频率分布直方图，如图12-12所示，图中从左到右各小组的长方形的高的比是1∶3∶6∶4∶2，最右边一组的频数是6，结合直方图提供的信息，解答下列问题.。

用Excel做直方图（2）：频率分布直方图一、什么是直方图1、定义直方图是一种条形图，是以组距为底边、以频数为高度的一系列连接起来的直方型矩形图2、相关概念组数：在统计数据时，把数据按照不同的范围分成几个组，分成的组的个数称为组数。

组距：每一组两个端点的差规格上限：Tu规格下限：Tl公差中心：M=3、步骤1. 求出其最大值和最小值。

2. 将数据分成若干组，并做好记号。

3. 计算组距的宽度。

用最大值和最小值之差（极差）去除组数，求出组距的宽度。

4. 计算各组的界限位。

各组的界限位可以从第一组开始依次计算，第一组的下界为最小值减去最小测定单位的一半，第一组的上界为其下界值加上组距。

第二组的下界限位为第一组的上界限值，第二组的下界限值加上组距，就是第二组的上界限位，依此类推。

5. 统计各组数据出现频数，作频数分布表。

6. 作直方图。

以组距为底长，以频数为高，作各组的矩形图。

4、注意事项：1. 数据量在50个以上2. 分组数在5~12个为宜3. 在直方图上应标注出公差范围(T)、样本容量(n)、样本平均值(x)、样本标准偏差值(s)和x的位置二、实战：用Excel做直方图1、获取数据源按照上节内容讲的随机数发生器，我们随机生成均值为0，标准差为1的100个符合正态分布的数据，用这100个数据来做频率分布直方图。

生成的数据如A列所示。

2、计算相应值我们要算出这组数据的个数，最大值、最小值、平均值、极差（最大值-最小值）、组数和组距。

相应的公式如下图所示。

组数：其中组数是这组数组被分成组的个数，是对数据个数开方然后向上取整求出。

组距：组距是每一组数两个端点的差，用极差除以组数求得。

这里提供另外一种直接生成数据描述性统计分析的值的方法，Excel——数据分析工具库——描述统计分析工具，直接生成关于一组数据的“描述统计”分析工具用于生成数据源区域中数据的单变量统计分析报表，组数和组距还是要手动公式输入，这里的描述性统计分析只是用来提供有关数据趋中性和易变性的信息。

用Excel生成频率分布表及频率分布直方图在统计教与学中，对数据进行统计分析、绘制统计图表等，要涉及许多繁琐复杂的计算与制图过程。

若单凭手工进行，将十分费事、单调烦人，而且容易出错。

Excel提供了众多功能强大的统计函数及分析工具。

借助它们，解决同样的问题，省时高效又完美。

本文以生成频率分布表及频率分布直方图为例，介绍运用“分析工具”的具体过程。

一、调用分析工具的方法“分析工具库”包括下述工具：方差分析、描述分析、相关分析、直方图、随机函数发生器、抽样分析、回归分析、z-检验等。

若要访问这些工具，应先单击“工具”菜单中的“数据分析”。

首次调用，需先加载宏“分析工具库”。

步骤如下：（1）在“工具”菜单上，单击“加载宏”。

（2）在“有用加载宏”列表中，选中“分析工具库”框，再单击“确定”。

（3）选择“工具”菜单中的“数据分析”，出现“数据分析”对话框，单击要使用的分析工具的名称，再单击“确定”。

在已选择的分析工具对话框中，设置所需的分析选项。

二、生成频率分布表及频率分布直方图的步骤1．用课本的方法对数据分组例如，高中新课标教科书数学必修3《统计》（人教A2007版）P66中关于100位居民的月均用水量，以0．5为组距将它们分成以下9组：[0, 0.5]，（0.5，1],…,(4, 4.5] 2．输入数据与分点的值（1）为方便起见，将100个数据以方阵形式输入到Excel的工作表中的适当区域；（2）将各组区间的右端点的值输入到作表中的同一列（如A列）。

3．生成频数分布表（直方图）、累积频率分布表（直方图）(1)打开“工具/数据分析”，在分析工具窗口中选择“直方图”；(2)在直方图弹出窗口（如下图所示）的“输入区域”利用MOUSE或键盘输入数据方阵“100位居民的月均用水量区域”：$B$2: $K$12；在“接收区域” 用同样的方法输入“分点数据”区域：$A$2: $A$10； (3)在输出选项中，点击“输出区域”，输入三列十行的区域，如：$M$16: $O$25； (4)在输出选项中，点击“图表输出”。

体育成绩频数分布直方表
体育成绩频数分布直方表是一种统计图表，用于显示不同成绩区间的频数分布。

它由一个X轴和一个Y轴组成，X轴表示
成绩区间，Y轴表示该区间内的频数。

下面是一个示例的体育成绩频数分布直方表：
成绩区间频数
60-69 3
70-79 6
80-89 7
90-100 4
这个直方表显示了某个班级学生在体育考试中的成绩分布情况。

例如，在60-69分数段内有3个学生，70-79分数段内有6个
学生，以此类推。

通过直方表，我们可以更直观地了解成绩分布情况，比如哪个分数段的学生人数最多或最少，平均成绩是多少等。

频数及其分布一：基本定义1.极差：一组数据的最大值与最小值的差组别(kg) 2.75～3.15 3.15～3.55 3.55～3.95 3.95～4.35 4.35～4.75 4.75～5.15 划 记 ┬ 正┬ 正 一 ┬ ┬ 一 人 数 2 7 6 2 2 1合计202.频数：我们称数据分组后落在各小组内的数据个数为频数； 频数分布表：反映数据分布的统计表叫做频数分布表，也称频数表。

3.频率：一般地，每一组频数与数据总数（或实验总次数）的比，叫做这一组数 据的频率.例 1：填写下面这张频数分布表中未完成部分.组别 A B C D 合计频数 11 13频率 0.11 0.66 0.10变式：学生各组数据频率之和等于多少？所有频数之和呢？例 2：已知一组数据的频率为 0.35，数据总数为 500 个，则这组数据的频数为 变式：已知一组数据的频数为 56，频率为 0.8，则数据总数为 个例 3 某袋装饼干的质量的合格范围为 50±0.125g.抽检某食品厂生产的 200 袋该中饼干，质 量的频数分布如下表. （1） 求各组数据的频率； （2） 由这批抽检饼干估计该厂生产这种饼干的质量的合格率.某食品厂生产的 200 袋饼干的质量的频数分布表组别（g） 49.775～49.825 49.825～49.875 49.875～49.925 49.925～49.975 49.975～50.025 50.025～50.075 50.075～50.125 50.125～50.175组中值（g） 49.80 49.85 49.90 49.95 50.00 50.05 50.10 50.15频数 1 2 1 50 100 40 4 2频率二：频数分布直方图一：用来表示频数分布的基本统计图叫做频数分布直方图，简称直方图(Mstogram)． 在统计数据时，按照频数分布表，在平面直角坐标系中，横轴标出每个组的端点，纵轴 表示频数，每个矩形的高代表对应的频数，我们称这样的统计图为频数分布直方图，如图 12-5 所示，直方图中各矩形之间没有空隙.【说明】 在画频数分布直方图时，首先要列出频数分布表.在分组时要注意： （1）组 数适当； （2）组距相等. 同时，分组要遵循三个原则： （1）不空，即该组必须有数据； （2）不重，即一个数据只 能在一个组中； （3）不漏，即不能漏掉某一个数据.思考：频数分布直方图与条形统计图的区别？（1）条形统计图中，横轴上的数据是孤立的，是一个具体的数据。