第四章 地下水向完整井的非稳定运动

内容主要有：（1）渗流理论基础；（2）地下水向河渠的稳定运动；（3）地下水向完整井的稳定运动；（4）地下水向完整井的非稳定运动；（5）地下水向边界附近井的稳定和非稳定运动。

重点考核地下水运动的基本概念、基本原理和方法。

题目类型有名词解释、判断题、作图题和计算题等，其中计算题占试题总分数的65%。

《地下水动力学》复习要点第一章 渗流理论基础一、基本内容1、基本概念：多孔介质、贮水率、贮水系数（弹性给水度）、渗流、渗流速度及与实际速度关系、水头（位置水头、测压管水头）、水力坡度、渗透系数、渗透率、导水系数、各向异性介质、各向同性介质、均质与非均质、水流折射原理、流网、dupuit 假设、第一类边界条件、第二类边界条件等2、基本定律：达西定律及适用范围3、描述地下水运动的方程：渗流连续性方程、承压水运动的基本微分方程、潜水运动的基本微分方程、越流含水层地下水非稳定流运动方程4、定解条件（初始条件、边界条件），数值方法基本思想二、要求1、理解并掌握上述概念和理论2、用达西定律分析水头线的变化或根据流网分析水文地质条件变化；3、给定水文地质条件，能正确画出反映地下水运动特点的流网图；4、给定水文地质模型和水文地质条件，写出反映地下水运动的基本方程（给定假设条件，建立数学模型，包括初始条件、边界条件）第二章 河间地块地下水的稳定运动一、基本内容有入渗时河间地块潜水的稳定运动问题（水文地质模型、假设条件、数学模型、流网、任意过水断面流量、分水岭移动规律、水头线）、无入渗时潜水的稳定运动、承压水的稳定运动，水在承压—无压含水层中的运动，非均质含水层中水的运动问题。

二、学习要求根据给定问题的水文地质条件，用相关公式计算过水断面流量或水位。

三、常用公式 1、承压含水层（达西定律） l H H m m kq 21212++= x lH H H H 211--= 2、无入渗潜水含水层（达西定律）l h h h h k q 21212-+= x lh h h h 2122212-+= 3、有入渗时潜水 wx wl l h h k q +--=2122221 )(22122212x lx kw x l h h h h -+-+= 4、分水岭位置 l h h w k l a 222221--= 5、其它流动问题（水平层状含水层、非均质含水层、承压—无压含水层、厚度或水流厚度沿流向变化等）第三章 地下水向完整井的稳定运动一、 基本概念：完整井、不完整井、水井及周围水位（水头）、稳定井流条件（定水头边界、越流、入渗补给）、井损与水跃、影响半径与引用影响半径、叠加原理、均匀流及平面或剖面流网二、学习要求1、掌握地下水向承压水井和潜水井运动问题的假设条件、数学模型、平面或剖面流网特征2、利用有关公式计算抽水量、降深或利用抽水试验资料（已知降深或水位），求含水层参数（导水系数或渗透系数）3、应用叠加原理地下水向完整井群的稳定运动问题。

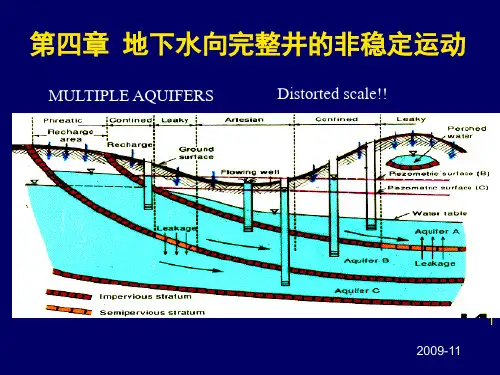
第四章 地下水向完整井的非稳定运动§1、承压含水层中的完整井流一、定流量抽水时的Theis(泰斯公式)假定条件：（1）含水层均质各向同性、等厚，侧向无限延伸，产状水平； （2）抽水前天然状态下水力坡度为零； （3）完整井定流量抽水，井径无限小； （4）含水层中水流服从Darcy 定律；（5）水头下降引起的地下水从贮存量中的释放是瞬时完成的。

教学模型的建立和求解：抽水形成以井轴为对称轴的下降漏斗，将坐标原点放在含水层底板抽水井的井轴处，井轴为z 轴，建立坐标系。

则以降深表示的微分方程为：教学模型为： 其解为：其中：s —抽水影响范围内，任一点任一时刻的水位降深；Q —抽水井的流量； T —导水系数；t —自抽水开始导计算时刻的时间； r —计算点到抽水井的距离； u —含水层的贮水系数。

利用上述W(u)和u 的关系制定P 93表，W(u)可查表得。

首先由 计算出u 値，然后查表得相应的W(u)，再求r 处的s 値。

tsT urs r rs ∂∂=∂∂+∂∂*221⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧-=∂∂>=∂∂=∞∞<<=∞<<>∂∂=∂∂+∂∂→∞→T r s r t r s t s r r s r t t s T u rs r r s r r π2Qlim 00,0),(00)0,(0,010*22()()⎰∞-===uy dy y e u W Tt u r u u W T Q s 44*2πTtu r u 4*2=二、流量变化时的计算公式流量随时间的变化，可分为阶梯变化和连续渐变，相应的流量过程线为台阶状和连续光滑的曲线。

连续光滑的曲线应概括成阶梯状折线。

概化的原则：矩形面积等于曲线与横坐标所围成的面积。

每一个阶梯视为定流量，用Theis 公式计算降深,然后将各降深叠加起来，得流量变化的总降深値。

如图，连续抽水，概括为4个阶梯，若求t 时刻的水位降深，则可分解为四个亚问题，第一个亚问题以Q 1流量抽水从t 0→t ；第二个亚问题以Q 2－Q 1流量抽水，从t 1→t ；第三个亚问题以Q 3－Q 2流量抽水从t 2→t ；第四个亚问题以Q 4－Q 3流量抽水从t 3→t 。

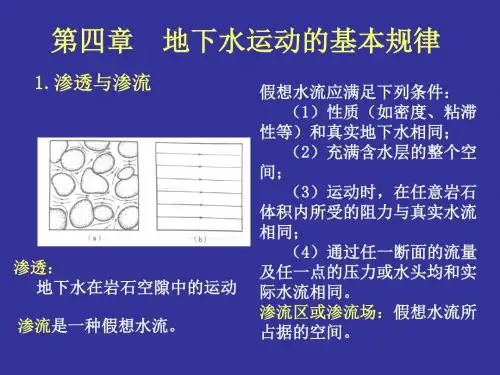
供水水文地质第四章地下水的运动第四章地下水的运动地下水的运动就是地下水在岩层空隙中流动过程的特征和规律。

4.1 地下水运动的特征及其基本规律一、地下水运动的特点（一）曲折复杂的水流通道：渗流模型（二）迟缓的流速：地下水在曲折的通道中缓慢地流动称为渗流，或称渗透水流。

（三）层流和紊流（四）非稳定、缓变流运动；稳定渗流——在渗流场内各运动要素（流速、流量、水位）不随时间变化的地下水运动，称为稳定渗流。

非稳定渗流——在渗流场内各运动要素在渗流过程中随时间随时间改变的地下水运动，为非稳定渗流。

二、地下水运动的基本规律线性渗透定律反映了地下水作层流运动时的基本规律，是法国水力学家达西建立的，所以称为达西定律。

达西渗透定律：水在土中的渗流量Q除了与试样的截面积A及渗流时间t成正比外，还与试样两端的水头差（h1-h2）成正比，与渗径长度L成反比。

渗透流速与水力梯度成正比——达西定律为线性渗透定律k——渗透系数（单位水力梯度作用下孔隙流体的渗流速度）（二）非线性渗透定律4.2 地下水流向井的稳定运动一、地下水取水构筑物的基本类型：1. 潜水完整井：凿井至潜水含水层底板（隔水层），水流从井的四周流入井内。

2. 潜水非完整井：凿井未到含水层底板，地下水可以从井底及井的四周进入井内。

3. 承压水完整井：凿穿承压含水层顶板，并穿透整个含水层，水流从四周流入井内。

4．承压水非完整井：凿穿承压含水层顶板后仅穿透一部分含水层，地下水可从井的四周及井底进入井内。

二、地下水流向潜水完整井裘布依公式可以解决的两方面问题1．求含水层的渗透系数k——在水源勘察时常常是通过现场实测Q、S、H0、R、r，然后计算含水层的k值。

2．预计潜水完整井的出水量Q——在水源设计时往往是已知或假设公式中的参数H0、S、k、R、r，然后推算出设计井的预计出水量Q。

三、地下水流向承压水完整井地下水向承压水完整井运动的裘布依公式。

四、裘布依（Dupuit)公式的讨论1．抽水井流量与水位降深的关系2 ．抽水井流量与井径的关系3 ．水跃对Dupuit 公式计算结果的影响4 ．井的最大流量问题4.3 地下水流向井的非稳定运动泰斯非稳定流理论认为，在抽水过程中，地下水的运动状态是随时间而变化的，即动水位不断下降，降落漏斗不断扩大，直至含水层的边缘或补给水体。

第四章地下水向完整井的非稳定运动一、填空题1．泰斯公式的适用条件中含水层为____________的承压含水层；天然水力坡度近为_______；抽水井为______________，井流量为_________；水流为_____________。

2．在泰斯井流中，渗流速度随时间的增加而_______，当时渗流速度就非常接近_________。

3．定降深井流公式反映了抽水期间井中水位___________，而井外水位_________，井流量随时间延续而___________的井流规律。

4．泰斯井流中没有“影响半径”这个概念，但通常取用“引用影响半径”，其表达式为____________。

5．潜水非稳定井流与承压井流比较，主要不同点有三点：⑴导水系数是__________；⑵当降深较大时___________不可忽略；⑶从含水层中抽出的水量主要来自___________。

6．博尔顿第一模型主要是考虑了____________；第二模型主要考虑了_________。

7．第一越流系统是指不考虑__________和忽略____________的越流系统；第二越流系统是指考虑____________而不考虑____________的越流系统；第三越流系统是指考虑____________而忽略____________的越流系统。

8．将泰斯公式近似地应用于潜水井流的条件是____________，当井流降深S＜0.1H0(含水层初始厚度)时,公式形式为____________;当0.1H0＜s＜0.3HO时,公式形式为____________。

二、判断题1．根据Theis公式，降深S随井函数自变量u的增大而增大。

（）2．当涌水量Q为定值时，Theis公式中的降深与井半径成正比。

（）3．经过一定的抽水时间之后，在一定的径距范围内，承压漏斗曲线平行地下降。

（）4．非稳定抽水条件下，通过抽水井周围任一圆柱形过水断面的流量都等于抽水量。

4 地下水向完整井的非稳定运动要点：本章主要介绍地下水非稳定井流的有关公式及应用。

非稳定井流公式主要包括承压井流泰斯（Theis ）公式、雅柯布（Jacob ）公式、流量呈阶梯状变化时计算公式、恢复水位公式、定降深公式、不同条件下的越流公式以及无外界补给的潜水井流的博尔顿（ Boulton ）及纽曼（Neuman ）公式。

上述可以用于相应条件下的动态预报，以及利用抽水试验资料求含水层的水文地质参数等。

本章是全书重点之一。

要求学生掌握各公式及其适用条件，并能用来分析解决实际问题；掌握如何用抽水试验资料确定水文地质参数的方法。

4.1 无限分布的承压完整井流本节主要介绍泰斯公式及其求参数方法，如表4—1所示。

此外介绍均质各向异性岩层式中：y x T T T *称为等效导水系数；y x T T ,—分别为长、短轴主渗透方向上的导水系数；)(n u W —泰斯井函数；)4/(2*t T r u n n ，式中的T n 为与x （长）轴成)(n 夹角方向上的导水系数，其值为： )(sin )(cos 22n n xn T T（4-2） 式中：θ—第一条观测线（即第一观测孔与抽水井的联线）与x 轴（长轴方向）的夹角。

注：表中（W（u））、〔u〕、（s）、（t）等为配合点的坐标值;t0，P0，（t/r2）0为直线在相应横轴上的截距；t s、r s、、（t/r2）为直线在纵轴上截距为s0时的对应横坐标值，i为直线的斜率，s A、t A为曲线上任一点坐标值。

如图4-1(b)所示：a n —第n 条观测线与第一观测线的夹角；22222*sin )(sin )(cos cos )(n n n n v y x b b T T T T (4-3) n n T T b 1;由212T T b 和313T Tb 联立求解有： 3222233222232sin )1(2sin )1(sin )1(sin )1(22 b b b b tg （4-4） *2**T b a r T T a b T T b a T ss n n s s y s s x ；；s s b a 、—分别为椭圆长短主轴的长度。

《地下水动力学》习题集第一章渗流理论基础一、解释术语1. 渗透速度：又称渗透速度、比流量，是渗流在过水断面上的平均流速。

它不代表任何真实水流的速度，只是一种假想速度。

记为v，单位m/d。

2. 实际速度：孔介质中地下水通过空隙面积的平均速度；地下水流通过含水层过水断面的平均流速，其值等于流量除以过水断面上的空隙面积，量纲为L/T。

记为_ u。

3. 水力坡度：在渗流场中，大小等于梯度值，方向沿着等水头面的法线，并指向水头降低方向的矢量。

4. 贮水系数：又称释水系数或储水系数，指面积为一个单位、厚度为含水层全厚度M的含水层柱体中，当水头改变一个单位时弹性释放或贮存的水量，无量纲。

m* = ms M。

5. 贮水率：指当水头下降（或上升）一个单位时，由于含水层内骨架的压缩（或膨胀）和水的膨胀（或压缩）而从单位体积含水层柱体中弹性释放（或贮存）的水量，量纲1/L。

ms = rg (a+nb)。

6. 渗透系数：也称水力传导系数，是表征岩层透水性的参数，影响渗透系数大小的主要是岩石的性质以及渗透液体的物理性质，记为K。

是水力坡度等于1时的渗透速度。

单位：m/d或cm/s。

7. 渗透率：表征岩层渗透性能的参数；渗透率只取决于岩石的性质，而与液体的性质无关，记为k。

单位为cm2或D。

8. 尺度效应：渗透系数与试验范围有关，随着试验范围的增大而增大的现象，K=K(x)。

9. 导水系数：是描述含水层出水能力的参数；水力坡度等于1时，通过整个含水层厚度上的单宽流量；亦即含水层的渗透系数与含水层厚度之积，T=KM。

它是定义在一维或二维流中的水文地质参数。

单位：m2/d。

二、填空题1．地下水动力学是研究地下水在孔隙岩石、裂隙岩石和岩溶岩石中运动规律的科学。

通常把具有连通性的孔隙岩石称为多孔介质，而其中的岩石颗粒称为骨架。

多孔介质的特点是多相性、孔隙性、连通性和压缩性。

2．地下水在多孔介质中存在的主要形式有吸着水、薄膜水、毛管水和重力水，而地下水动力学主要研究重力水的运动规律。