无限深势阱 势垒
- 格式:pdf
- 大小:641.58 KB
- 文档页数:4
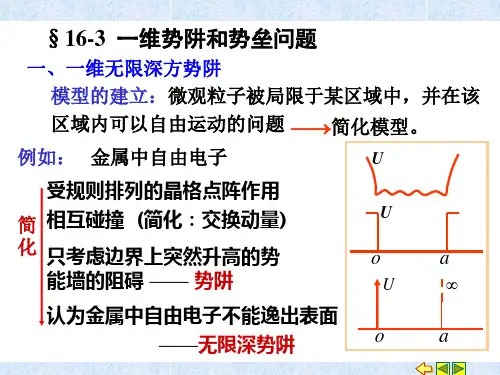

一维对称无限深方势阱的波函数表达式在量子力学中,一维对称无限深方势阱是一种经典的势阱模型,它在研究粒子在受限空间内的运动和能级结构等方面有很好的应用。
对于一维对称无限深方势阱来说,波函数的表达式是非常重要的,它可以帮助我们理解粒子在势阱内的行为以及计算其能级。
1. 势阱模型的基本假设一维对称无限深方势阱模型假设了以下几点:势阱的宽度为a,势阱内部的势能为0,而在势阱外部势能为无穷大,这意味着粒子在势阱内运动自由,在势阱外不能存在。
这是一个理想化的模型,但对于研究粒子在受限空间内的行为却是非常有用的。
2. 薛定谔方程的求解根据薛定谔方程,我们可以求解一维对称无限深方势阱中的波函数。
薛定谔方程的一般形式为:-ħ²/2m * d²Ψ/dx² + V(x)Ψ = EΨ其中,ħ是普朗克常数,m是粒子的质量,V(x)是势能函数,Ψ是波函数,E是能量。
对于无限深方势阱来说,势能函数V(x)在势阱内为0,在势阱外为无穷大,因此薛定谔方程可以简化为:-ħ²/2m * d²Ψ/dx² = EΨ4. 波函数的边界条件在一维对称无限深方势阱中,波函数的边界条件非常明确,因为势能在势阱外为无穷大,粒子无法透过势垒逃逸出去,故波函数在势阱外为0。
而在势阱内部,波函数要满足Ψ(0) = Ψ(a) = 0,这是因为势阱的边界为0。
5. 波函数的表达式根据边界条件,我们可以求解出一维对称无限深方势阱中的波函数表达式。
在势阱内部,波函数的一般形式为:Ψ(x) = Asin(kx) + Bcos(kx)其中,A和B是待定系数,k是波数,根据波函数的边界条件,我们可以求解出波函数的具体形式。
在势阱内部,波函数的波数k为:k = sqrt(2mE) / ħ对于一维对称无限深方势阱,能级是分立的,即E = n²π²ħ² / (2ma²),其中n为正整数。



量子力学中的无限深势阱问题量子力学是描述微观世界的物理学理论,它在解释和预测微观粒子行为方面具有重要的作用。
其中,无限深势阱问题是量子力学中的一个经典问题,它帮助我们理解波函数的性质以及粒子在势场中的行为。
无限深势阱问题是指一个粒子被限制在一个势能在某个区域内为无限大,在区域外为零的势场中运动。
这个问题可以用一维的情况来描述,假设势阱的宽度为L,那么势阱内的势能函数可以表示为:V(x) = 0, 0 < x < LV(x) = ∞, x < 0 或者 x > L在经典力学中,粒子在势场中的运动是由牛顿第二定律描述的,而在量子力学中,粒子的运动状态由波函数来描述。
波函数是量子力学中的基本概念,它是一个复数函数,可以用来描述粒子的位置和动量。
对于无限深势阱问题,我们可以使用定态薛定谔方程来求解。
定态薛定谔方程可以表示为:-ħ²/2m * d²ψ(x)/dx² + V(x)ψ(x) = Eψ(x)其中ħ是普朗克常数的约化形式,m是粒子的质量,E是粒子的能量,ψ(x)是粒子的波函数。
在势阱内部,势能V(x)为零,因此定态薛定谔方程可以简化为:-ħ²/2m * d²ψ(x)/dx² = Eψ(x)这是一个简化的定态薛定谔方程,可以通过求解这个方程来得到粒子在势阱内部的波函数。
根据边界条件,当x=0或者x=L时,势能V(x)为无穷大,因此波函数必须为零。
这意味着在势阱的两个边界处,波函数的值为零。
根据上述条件,我们可以得到波函数的一般形式为:ψ(x) = A * sin(kx)其中A是归一化常数,k是波数,可以通过边界条件来确定。
当x=0时,波函数为零,因此有sin(0) = 0,这意味着kx = 0,即k = 0。
当x=L时,波函数为零,因此有sin(kL) = 0,这意味着kL = nπ,其中n是一个整数。
通过边界条件,我们可以得到k的取值为:k = nπ/L由于波函数必须是归一化的,我们可以通过归一化条件来确定归一化常数A。



量子力学中一维无限深势阱问题两种解题方法的比较一维无限深势阱是量子力学中一个经典的问题,可以用两种方法进行求解:定态微扰论和定态井底近似。
1. 定态微扰论:定态微扰论是量子力学中解决简单势场问题常用的一种方法。
在无限深势阱问题中,可以将无穷深方势阱视为定态问题的微扰,将该势场加入到系统的哈密顿量中,然后使用微扰论进行求解。
定态微扰论的步骤如下:- 首先,将无限深方势阱问题的哈密顿量记为H0,并找到H0的本征函数和本征能量。
- 然后,将无穷深势阱视为微扰,将微扰项H'加入到哈密顿量。
- 使用微扰论的公式,展开本征函数和本征能量的泰勒级数,得到微扰的一阶修正项。
- 最后,将微扰项的一阶修正项加到H0的本征能量上,得到精确的能级修正。
2. 定态井底近似:定态井底近似是另一种求解一维无限深势阱问题的常用方法。
该方法的核心思想是将无穷深方势阱问题看作是薛定谔方程在势能井底附近的近似解。
定态井底近似的步骤如下:- 首先,将无限深方势阱的势能井底近似为一个宽度为a的矩阵势阱,且矩阵势阱的势垒高度为无穷大。
- 然后,将定态薛定谔方程在矩阵势阱内求解,得到在该势阱内的本征函数和本征能量。
- 最后,将势能井底趋于无穷深,即将势阱的势垒高度取极限使其趋于无穷大,此时得到的本征函数和本征能量就是无限深方势阱问题的精确解。
比较两种方法:- 定态微扰论适用于一般情况下的微扰问题,可以求得很多物理量的修正。
但是在计算过程中需要进行级数展开,需要考虑到每一阶的修正项,计算较为复杂。
- 定态井底近似是一种近似方法,适用于无穷深方势阱问题的求解。
它将无穷深方势阱问题转化为一个简单的矩阵势阱问题,简化了问题的求解过程。
- 在求解一维无限深势阱问题时,定态井底近似更加简单快速,能够直接得到问题的精确解。
而定态微扰论的应用范围更广,在求解一些复杂问题时更具有优势。
综上所述,定态井底近似适用于一维无限深势阱问题的精确解,而定态微扰论适用于更一般的微扰问题,并具有更广泛的应用范围。

