压力管道水力计算
- 格式:ppt
- 大小:2.46 MB
- 文档页数:48

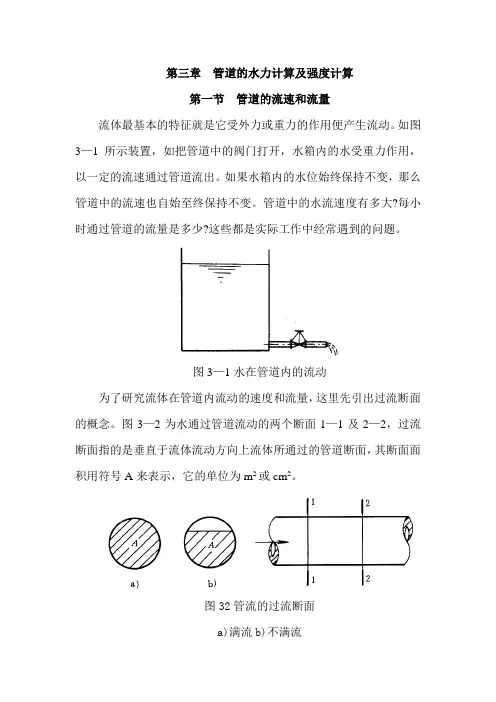
第三章管道的水力计算及强度计算第一节管道的流速和流量流体最基本的特征就是它受外力或重力的作用便产生流动。
如图3—1所示装置,如把管道中的阀门打开,水箱内的水受重力作用,以一定的流速通过管道流出。
如果水箱内的水位始终保持不变,那么管道中的流速也自始至终保持不变。
管道中的水流速度有多大?每小时通过管道的流量是多少?这些都是实际工作中经常遇到的问题。
图3—1水在管道内的流动为了研究流体在管道内流动的速度和流量,这里先引出过流断面的概念。
图3—2为水通过管道流动的两个断面1—1及2—2,过流断面指的是垂直于流体流动方向上流体所通过的管道断面,其断面面积用符号A来表示,它的单位为m2或cm2。
图32管流的过流断面a)满流b)不满流流量是指单位时间内,通过过流断面的流体体积。
以符号q v表示,其单位为m3/h,cm3/h或m3/s,cm3/s。
流速是指单位时间内,流体流动所通过的距离。
以符号。
表示,其单位为m/s或cm/s。
图3—3管流中流速、流量、过流断面关系示意图流量、流速与过流断面之间的关系如下:以水在管道中流动为例,如图3—3所示,在管段上取过流断面1—1,如果在单位时间内水从断面1—1流到断面2—2,那么断面1—1和断面2—2所包围的管段的体积即为单位时间内通过过流断面1—1时水的流量q v,而断面1—1和断面2—2之间的距离就是单位时间内水流所通过的路程,即流速。
由上可知,流量、流速和过流断面之间的关系式为q v=vA (3—1) 式(3—1)叫做流量公式,它说明流体在管道中流动时,流速、流量和过流断面三者之间的相互关系,即流量等于流速与过流断面面积的乘积。
如果在一段输水管道中,各过流断面的面积及所输送的水量一定,即在管道中途没有支管与其连接,既没有水流出,也没有水流入,那么管道内各过流断面的水流速度也不会变化;若管段的管径是变化的(即过流断面的面积A是变化的),那么管段中各过流断面处的流速也随着管径的变化而变化。

流量与管径、压力、流速的一般关系一般工程上计算时,水管路,压力常见为,水在水管中流速在1--3米/秒,常取米/秒。
流量=管截面积X流速=管内径的平方X流速(立方米/小时)。
其中,管内径单位:mm ,流速单位:米/秒,饱和蒸汽的公式与水相同,只是流速一般取20--40米/秒。
水头损失计算Chezy 公式这里:Q ——断面水流量(m3/s)C ——Chezy糙率系数(m1/2/s)A ——断面面积(m2)R ——水力半径(m)S ——水力坡度(m/m)根据需要也可以变换为其它表示方法:Darcy-Weisbach公式由于这里:h f——沿程水头损失(mm3/s)f ——Darcy-Weisbach水头损失系数(无量纲)l ——管道长度(m)d ——管道内径(mm)v ——管道流速(m/s)g ——重力加速度(m/s2)水力计算是输配水管道设计的核心,其实质就是在保证用户水量、水压安全的条件下,通过水力计算优化设计方案,选择合适的管材和确经济管径。
输配水管道水力计算包含沿程水头损失和局部水头损失,而局部水头损失一般仅为沿程水头损失的5~10%,因此本文主要研究、探讨管道沿程水头损失的计算方法。
管道常用沿程水头损失计算公式及适用条件管道沿程水头损失是水流摩阻做功消耗的能量,不同的水流流态,遵循不同的规律,计算方法也不一样。
输配水管道水流流态都处在紊流区,紊流区水流的阻力是水的粘滞力及水流速度与压强脉动的结果。
紊流又根据阻力特征划分为水力光滑区、过渡区、粗糙区。
管道沿程水头损失计算公式都有适用范围和条件,一般都以水流阻力特征区划分。
水流阻力特征区的判别方法,工程设计宜采用数值做为判别式,目前国内管道经常采用的沿程水头损失水力计算公式及相应的摩阻力系数,按照水流阻力特征区划分如表1。
沿程水头损失水力计算公式和摩阻系数表1阻力特征区适用条件水力公式、摩阻系数符号意义水力光滑区>10雷诺数h:管道沿程水头损失v:平均流速d:管道内径γ:水的运动粘滞紊流过渡区10<<500(1)(2)紊流粗糙区>500系数λ:沿程摩阻系数Δ:管道当量粗糙度q:管道流量Ch:海曾-威廉系数C:谢才系数R:水力半径n:粗糙系数i:水力坡降l:管道计算长度达西公式是管道沿程水力计算基本公式,是一个半理论半经验的计算通式,它适用于流态的不同区间,其中摩阻系数λ可采用柯列布鲁克公式计算,克列布鲁克公式考虑的因素多,适用范围广泛,被认为紊流区λ的综合计算公式。

压力管道的水力计算和经济直径的确定一、水力计算压力管道的水力计算包括恒定流计算和非恒定流计算两种。
(一)恒定流计算恒定流计算主要是为了确定管道的水头损失。
管道的水头损失对于水电站装机容量的选择、电能的计算、经济管径的确定以及调压室稳定断面计算等都是不可缺少的。
水头损失包括摩阻损失和局部损失两种。
1、摩阻损失管道中的水头损失与水流形态有为。
水电站压力管道中的水流的雷诺数Re一般都超过3400,因而水流处于紊流状态,摩阻水头损失可用曼宁公式或斯柯别公式计算。
曼宁公式应用方便,在我国应用较广。
该公式中,水头损失与流速平方成正比,这对于钢筋混凝土管和隧洞这类糙率较大的水道是适用的。
对于钢管,由于糙率较小,水流未、能完全进人阻力平方区,但随着时间的推移,管壁因锈蚀糙率逐渐增大,按流速平方关系计算摩阻损失仍然是可行的。
曼宁公式因一般水力学书中均可找到,此处从略。
斯柯别根据198段水管的1178个实测资料,推荐用以下公式计算每米长钢管的摩阻损失(13-1)式中a-水头损失系数,焊接管用0.00083。
为考虑水头损失随使用年数t的增加而增大的系数,清水取K=0.01,腐蚀性水可取K=0.015。
2.局部损失在流道断面急剧变化处,水流受边界的扰动,在水流与边界之间和水流的内部形成旋涡,在水流质量强烈的混掺和大量的动量交换过程中,在不长的距离内造成较大的能量损失,这种损失通常称为局部损失。
压力管道的局部损失发生在进口、门槽、渐变段、弯段、分岔等处。
压力管道的局部损失往往不可忽视,一尤其是分岔的损失有时可能达到相当大的数值。
局部损失的计算公式通常表示为系数可查有关手册。
(二)非恒定流计算管道中的非恒定流现象通常称为水锤。
进行非恒定流计算的目的是为了推求管道各点i的动水压强及其变化过程,为管道的布置、结构设计和机组的运行提供依据。
非恒定流计算的内容见第九章。
二、管径的确定压力管道的直径应通过动能经济计算确定。
在第七章中我们已经研究了决定渠道和隧洞经济断面的方法,其基本原理对压力管道也完全适用,可以拟定几个不同管径的方案,进行誉比较,选定较为有利的管道直径,也可以将某些条件加以简化,推导出计算公式,直接求解。

流量与管径、压力、流速的一般关系一般工程上计算时,水管路,压力常见为0.1--0.6MPa,水在水管中流速在1--3米/秒,常取1.5米/秒。
流量=管截面积X流速=0.002827X管内径的平方X流速(立方米/小时)。
其中,管内径单位:mm ,流速单位:米/秒,饱和蒸汽的公式与水相同,只是流速一般取20--40米/秒。
水头损失计算Chezy 公式这里:Q ——断面水流量〔m3/s〕C ——Chezy糙率系数〔m1/2/s〕A ——断面面积〔m2〕R ——水力半径〔m〕S ——水力坡度〔m/m〕根据需要也可以变换为其它表示方法:Darcy-Weisbach公式由于这里:h f——沿程水头损失〔mm3/s〕f ——Darcy-Weisbach水头损失系数〔无量纲〕l ——管道长度〔m〕d ——管道内径〔mm〕v ——管道流速〔m/s〕g ——重力加速度〔m/s2〕水力计算是输配水管道设计的核心,其实质就是在保证用户水量、水压平安的条件下,通过水力计算优化设计方案,选择适宜的管材和确经济管径。
输配水管道水力计算包含沿程水头损失和局部水头损失,而局部水头损失一般仅为沿程水头损失的5~10%,因此本文主要研究、探讨管道沿程水头损失的计算方法。
1.1 管道常用沿程水头损失计算公式及适用条件管道沿程水头损失是水流摩阻做功消耗的能量,不同的水流流态,遵循不同的规律,计算方法也不一样。
输配水管道水流流态都处在紊流区,紊流区水流的阻力是水的粘滞力及水流速度与压强脉动的结果。
紊流又根据阻力特征划分为水力光滑区、过渡区、粗糙区。
管道沿程水头损失计算公式都有适用范围和条件,一般都以水流阻力特征区划分。
水流阻力特征区的判别方法,工程设计宜采用数值做为判别式,目前国内管道经常采用的沿程水头损失水力计算公式及相应的摩阻力系数,按照水流阻力特征区划分如表1。
沿程水头损失水力计算公式和摩阻系数表1阻力特征区适用条件水力公式、摩阻系数符号意义水力光滑区>10雷诺数h:管道沿程水头损失v:平均流速d:管道内径γ:水的运动粘紊流过渡区10<<500〔1〕〔2〕紊流粗糙区>500滞系数λ:沿程摩阻系数Δ:管道当量粗糙度q:管道流量Ch:海曾-威廉系数C:谢才系数R:水力半径n:粗糙系数i:水力坡降l:管道计算长度达西公式是管道沿程水力计算根本公式,是一个半理论半经验的计算通式,它适用于流态的不同区间,其中摩阻系数λ可采用柯列布鲁克公式计算,克列布鲁克公式考虑的因素多,适用范围广泛,被认为紊流区λ的综合计算公式。

水力计算公式选用水力计算是指利用水的流动性质进行流量、压力和速度等相关参数的计算。
在水力学中,常用的水力计算公式主要有流量计算公式、速度计算公式和压力计算公式。
下面将介绍几种常用的水力计算公式。
一、流量计算公式:1.泊松公式:流量计算公式是通过测定流速和截面积的方式来计算流量。
泊松公式是最常用的流量计算公式之一,其公式为:Q=A×v其中,Q为流量,A为流体通过的截面积,v为流速。
2.管道流量公式:当涉及到管道流量计算时,可以使用伯努利公式来计算流量,伯努利公式为:Q=π×r²×v其中,Q为流量,r为管道的半径,v为流速。
3.梯形槽流量公式:当涉及到梯形槽流量计算时,可以使用曼宁公式来计算流量,曼宁公式为:Q=(1.49/A)×R^(2/3)×S^(1/2)其中,Q为流量,A为梯形槽的横截面积,R为梯形槽湿周和横截面积之比,S为梯形槽的比降,1.49为曼宁系数。
二、速度计算公式:1.波速计算公式:在涉及到波浪速度计算时,可以使用波速公式进行计算,波速公式的一般形式为:c=λ×f其中,c为波速,λ为波长,f为频率。
2.重力加速度和液体高度差计算公式:当涉及到重力加速度和液体高度差计算时,可以使用水头计算公式,水头计算公式的一般形式为:H=v²/2g+z其中,H为水头,v为速度,g为重力加速度,z为液体的高度。
三、压力计算公式:1.应力计算公式:当涉及到液体对物体的压力计算时,可以使用应力计算公式,应力计算公式的一般形式为:P=F/A其中,P为压力,F为受力大小,A为受力的面积。
2.流体静压力计算公式:当涉及到流体的静压力计算时,可以使用静压力计算公式,静压力计算公式的一般形式为:P=ρ×g×h其中,P为压力,ρ为流体密度,g为重力加速度,h为液体的高度。
以上是一些常用的水力计算公式,可以根据不同的情况和具体要求选择合适的公式进行计算。

第十六篇%管道水力计算第一章%钢管和铸铁管水力计算一!计算公式!&按水力坡降计算水头损失水管的水力计算#一般采用以下公式&Q H ,!+lE 22-$!$#!#!%式中%Q ...水力坡降(,...摩阻系数(+l...管子的计算内径$(%(E...平均水流速度$(*h %(-...重力加速度#为3&1!$(*h2%!应用公式$!$#!#!%时#必须先确定求取系数,值的依据!对于旧的钢管和铸铁管&当F E#3&2W !"/!(时$E...液体的运动粘滞度#(2*h %#,H "&"2!"+l"&)($!$#!#2%当F E<3&2W !"/!(时,H !+l"&)!&/W !"#1I E ()F "&)($!$#!#)%或采用E H !&)W !"#$(2*h $水温为!"?%时#则,H "&"!43+l"&)!I "&1$4()F "&)($!$#!#0%管壁如发生锈蚀或沉垢#管壁的粗糙度就增加#从而使系数,值增大#公式$!$#!#2%和公式$!$#!#)%适合于旧钢管和铸铁管这类管材的自然粗糙度!将公式$!$#!#2%和公式$!$#!#0%中求得的,值代入公式$!$#!#!%中#得出的旧钢管和铸铁管的计算公式&当F #!&2(*h 时#Q H "&""!"4F2+l!&)$!$#!#/%当F <!&2(*h 时#’4!0!’第一章%钢管和铸铁管水力计算Q H "&"""3!2F 2+l!&)!I"&1$4()F "&)$!$#!#$%钢管和铸铁管水力计算表即按公式$!$#!#/%和$!$#!#$%制成!2&按比阻计算水头损失由公式$!$#!#0%求得比阻公式如下&DH Q ;2H "&""!4)$+l/&)$!$#!#4%钢管和铸铁管的D 值#列于表!$#!#0!二!水力计算表编制表和使用说明!&钢管及铸铁管水力计算表采用管子计算内径+l 的尺寸#见表!$#!#!!在确定计算内径+l 时#直径小于)""((的钢管及铸铁管#考虑锈蚀和沉垢的影响#其内径应减去!((计算!对于直径等于)""((和)""((以上的管子#这种直径的减小没有实际意义#可不必考虑!编制钢管和铸铁管水力计算表时所用的计算内径尺寸表!$#!#!钢%管%$((%水煤气钢管中等管径钢管公称直径M 8外%径M 内%径+计算内径+l 公称直径M 8外%径M 内%径+计算内径+l 铸铁管$((%内%径+计算内径+l 1!)&/"3&""1&""!2/!0$!2$!2//"03!"!4&""!2&/"!!&/"!/"!$1!01!044/40!/2!&2/!/&4/!0&4/!4/!30!40!4)!""332"2$&4/2!&2/2"&2/2""2!3!33!31!2/!202/))&/"24&""2$&""22/20/22/220!/"!03)202&2/)/&4/)0&4/2/"24)2/)2/22""!330"01&""0!&""0"&""24/2332432412/"203/"$"&""/)&""/2&"")"")2/)"/)"/)"")""4"4/&/"$1&""$3&"")2/)/!))!))!)/")$"1"11&/"1"&/"43&/")/")44)/4)/4!""!!0&""!"$&""!"/&""’1!0!’第十六篇%管道水力计算钢%管%$((%水煤气钢管中等管径钢管公称直径M 8外%径M 内%径+计算内径+l 公称直径M 8外%径M内%径+计算内径+l铸铁管$((%内%径+计算内径+l!2/!0"&""!)!&""!)"&""!/"!$/&""!/$&""!//&""2&表!$#!#2"表!$#!#)$中等管径钢管水力计算表%管壁厚均采用!"((#使用中如需精确计算#应根据所选用的管子壁厚的不同#分别对表!$#!#2"表!$#!#)中的!"""Q 和F 值或对表!$#!#0中的D 值加以修正!!"""Q 值和D 值的修正系数i !采用下式计算&i !H +l+l()m/&)$!$#!#1%式中%+l...壁厚!"((时管子的计算内径$(%#+l m...选用管子的计算内径$(%!修正系数i !值#见表!$#!#2!平均水流速度F 的修正系数i 2#采用下式计算&i 2H +l+l()m2$!$#!#3%修正系数i 2值#见表!$#!#)!)&按比阻计算水头损失时#公式$!$#!#4%只适用于平均水流速度F #!&2(*h 的情况!当F <!&2(*h 时#表!$#!#0中的比阻D 值#应乘以修正系数i )!i )可按下式计算&中等管径的钢管!"""Q 值和D 值的修正系数i !表!$#!#2公称直径M 8$((%壁%厚%(%$((%0/$413!"!!!2!2/!/"!4/2""22/2/"24/)"")2/)/""&$!"&$$"&4""&4)"&4$"&41"&1""&1!"&1)"&10"&$$"&4""&40"&44"&43"&1!"&1)"&10"&1/"&1$"&42"&4$"&43"&1!"&1)"&1$"&1$"&14"&11"&13"&41"&1!"&1)"&1/"&14"&11"&13"&3""&3!"&32"&1/"&11"&13"&3""&3!"&32"&3)"&3)"&30"&3/"&32"&3)"&30"&3/"&3/"&3$"&3$"&34"&34"&34!!!!!!!!!!!&"3!&"1!&"$!&"$!&"/!&"0!&"0!&")!&")!&")!&!1!&!$!&!)!&!2!&!"!&"3!&"1!&"4!&"4!&"$’3!0!’第一章%钢管和铸铁管水力计算中等管径钢管F 值的修正系数i 2表!$#!#)公称直径M 8$((%壁%厚%(%$((%0/$413!"!!!2!2/!/"!4/2""22/2/"24/)"")2/)/""&1)"&1/"&14"&13"&3""&3!"&32"&3)"&3)"&30"&1$"&11"&13"&3!"&32"&3)"&3)"&30"&30"&3/"&11"&3""&3!"&32"&3)"&30"&30"&3/"&3/"&3$"&3!"&32"&3)"&30"&3/"&3/"&3$"&3$"&3$"&34"&30"&3/"&3$"&34"&34"&34"&34"&34"&31"&31"&34"&34"&31"&31"&31"&31"&33"&33"&33"&33!!!!!!!!!!!&")!&")!&"2!&"2!&"2!&"2!&"!!&"!!&"!!&"!!&"4!&"/!&"/!&"0!&"0!&")!&")!&")!&"2!&"2钢管和铸铁管的比阻D 值表!$#!#0水煤气钢管中等管径钢管铸铁管公称直径M 8$((%D $;()*h %D $;7*h %公称直径M 8$((%D $;()*h %内径$((%D $;()*h %1!"!/2"2/)20"/"4"1"!""!2/!/"22//""""")23/""""11"3"""!$0)"""0)$4""3)1$"00/)"!!"1"213)!!$12$4&01$&2)))&3/22/&/)2&3/1&1"3!&$0)"&0)$4"&"3)1$"&"00/)"&"!!"1"&""213)"&""!!$1"&"""2$40"&""""1$2)"&""""))3/!2/!/"!4/2""22/2/"24/)"")2/)/"!"$&200&3/!1&3$3&24)0&1222&/1)!&/)/"&3)32"&$"11"&0"41/"4/!""!2/!/"2""2/")"")/"!/!3"!4"3)$/&)!!"&10!&1/3&"232&4/2!&"2/"&0/23i )H "&1/2!I "&1$4()F"&)$!$#!#!"%修正系数i )值#见表!$#!#/!’"20!’第十六篇%管道水力计算钢管和铸铁管D 值的修正系数i )表!$#!#/F $(*h %"&2"&2/"&)"&)/"&0"&0/"&/"&//"&$i )!&0!!&))!&2"!&20!&2"!&!4/!&!/!&!)!&!/F $(*h %"&$/"&4"&4/"&1"&1/"&3!&"!&!!&2i )!&!"!&"1/!&"4!&"$!&"/!&"0!&")!&"!/!&""0&钢管$水煤气管%的!"""Q 和F 值见表!$#!#$#钢管M8H !2/>)/"((的!"""Q 和F 值见表!$#!#4(铸铁管M 8H /">)/"((的!"""Q 和F 值见表!$#!#1#表中F 值为平均水流速度(*h!计算示例&3例!4%当流量;H !0.*h H "&"!0()*h 时#求管长.H )/""(#外径W 壁厚H !30W$((的钢管的水头损失!3解4%由表!$#!#!中查得外径MH !30((的钢管公称直径为M 8H !4/((#又由表!$#!#4中M 8H !4/((一栏内查得!"""Q H 0&!/#F H "&$(*h !因为管壁厚度不等于!"(($为$((%#故需对!"""Q 值加以修正!由表!$#!#2中查得修正系数i !H"&43!故水头损失为&,H Q i !.H 0&!/!"""W "&43W )/""H !!&04(按着比阻求水头损失时#由表!$#!#0中查得DH !1&3$$;以()*h 计%#因为平均水流速度F "&$(*h $小于!&2(*h %#故需对D 值加以修正!由表!$#!#/查得修正系数i )H !&!!/!修正系数i !仍等于"&43!故水头损失为&,H D i !i ).;2H !1&3$W "&43W !&!!/W )/""W "&"!02H !!&0$(同样#因为管壁厚度不等于!"((#也应对平均水流速度F 值加以修正#由表!$#!#)查得修正系数i 2H"&3!!则求得&FH "&$"W "&3!H "&//(*h 3例24%当流量;H 4.*h H "&""4()*h 时#求M 8H !/"((#管长.H 2"""(的铸铁管的水头损失!3解4%由表!$#!#1中查到&!"""Q H 2&0$(F H "&0"(*h #故,H Q .H 2&0$!"""W 2"""H 0&32(!按比阻D 值求水头损失时#由表!$#!#0中查得DH 0!&1/$;以()*h 计%!因为平均流速小于!&2(*h #故必须计入修正系数i )#当F H "&0"(*h 时#由表!$#!#/中查得i )H !&2"!故水头损失为&,H D i ).;2H 0!&1/W !&2"W2"""W"&""42H 0&32(’!20!’第一章%钢管和铸铁管水力计算钢管和铸铁管水力计算见表!$#!#$#!$#!#4#!$#!#1!’220!’第十六篇%管道水力计算’)20!’第一章%钢管和铸铁管水力计算’020!’第十六篇%管道水力计算’/20!’第一章%钢管和铸铁管水力计算’$20!’’420!’’120!’’320!’’")0!’’!)0!’’2)0!’’))0!’’0)0!’’/)0!’’$)0!’第十六篇%管道水力计算’4)0!’第一章%钢管和铸铁管水力计算’1)0!’第十六篇%管道水力计算’3)0!’第一章%钢管和铸铁管水力计算’"00!’第十六篇%管道水力计算’!00!’第一章%钢管和铸铁管水力计算’200!’第十六篇%管道水力计算第二章%塑料给水管水力计算一!计算公式Q H ,!+l F 22-$!$#2#!%式中%Q ...水力坡降(,...摩阻系数(+l...管子的计算内径$(%(F...平均水流速度$(*h %(-...重力加速度#为3&1!$(*h 2%!应用公式$!$#2#!%时#应先确定系数,值!对于各种材质的塑料管$硬聚氯乙烯管"聚丙烯管"聚乙烯等%#摩阻系数定为&,H "&2/X f "&22$$!$#2#2%式中%X f ...雷诺数(X f HF +l E$!$#2#)%其中%E ...液体的运动粘滞系数$(2*h %!当E H !&)W !"#$(2*h $水温为!"?%时#将公式$!$#2#2%和式$!$#2#)%中求得的,值代入公式$!$#2#!%中#进行整理后得到&Q H "&"""3!/;!&440+l0&440$!$#2#0%式中%;...计算流量$()*h %(+l...管子的计算内径$(%!塑料给水管水力计算表即按公式$!$#2#0%制成!二!水力计算表的编制和使用说明$!%为计算方便#水力计算表是按标准管的计算内径编制的!对于公称管径M 8H 1>!/((的塑料管#采用,轻工业部部标准5P 41>1".4/-中B 8H!&"F B 9$!"J -*c (2%规格的硬聚氯乙烯管的实际内径作为标准管计算内径!对于公称管径M 8H 2">)/"((的塑料’)00!’第二章%塑料给水管水力计算管#采用,轻工业部部标准5P 41>1".4/-中B 8H"&$F B 9$$J -*c (2%规格的硬聚氯乙烯管的实际内径作为标准管计算内径!$2%各种不同材质"不同规格的塑料管#由于计算内径互有差异#所以在进行水力计算时#应将查水力计算表所得的!"""Q 值和F 值#分别乘以阻力修正系数i !和流速修正系数i 2进行修正!i !H +l+l()m0&440$!$#2#/%i 2H +l+l()m 2$!$#2#$%式中%+l...标准管计算内径$(%(+l m...计算管计算内径$(%!$)%国产各种材质规格塑料管的i !"i 2数据见表!$#2#!"表!$#2#2和表!$#2#)!在表!$#2#!中#硬聚氯乙烯管和聚乙烯管规格取自,轻工业部部标准5P 41>1".4/-!在表!$#2#2中#聚丙烯管规格取自轻工业部聚丙烯管材标准起草小组!341年1月编制的,聚丙烯管材料暂行技术条件-!在表!$#2#)中#硬聚氯乙烯管和聚乙烯管规格取自,化工部部标准@P .$).$/-!其它材质"规格塑料管的i !"i 2可分别用公式$!$#2#/%和式$!$#2#$%自行计算!轻工业部部标准硬聚氯乙烯管及聚乙烯管i !!i 2值表!$#2#!材%质硬%聚%氯%乙%烯聚%乙%烯工作压力B -H"&$F B 9B -H !&"F B 9B -H "&0F B 9公称管径M 8$((%外径MW 壁厚$((%计算内径+lm$((%i !i 2外径MW 壁厚$((%计算内径+lm$((%i !i 2外径MW 壁厚$((%计算内径+lm$((%i !i 21!2W !&/3!!!2W !&/3!!!"!$W 2!2!!!$W 2!2!!!/2"W 2!$!!2"W 2!$!!2"2/W !&/22!!2/W 2&/2"!&/4$!&2!"2/W 22!!&203!&"312/)2W !&/23!!)2W 2&/24!&0"4!&!/0)2W 2&/24!&0"4!&!/0)20"W 2&")$!!0"W ))0!&)!0!&!2!0"W ))0!&)!0!&!2!0"/"W 2&"0$!!/"W )&/0)!&)1"!&!00/"W 002!&/00!&2""/"$)W 2&//1!!$)W 0//!&213!&!!2$)W //)!&/)1!&!314"4/W 2&/4"!!4/W 0$4!&2)2!&"321"3"W )10!!3"W 0&/1!!&!3"!&"4/!""!!"W )&/!")!!!!"W /&/33!&2"1!&"12’000!’第十六篇%管道水力计算材%质硬%聚%氯%乙%烯聚%乙%烯工作压力B -H"&$F B 9B -H !&"F B 9B -H "&0F B 9公称管径M 8$((%外径MW 壁厚$((%计算内径+lm$((%i !i 2外径MW 壁厚$((%计算内径+lm$((%i !i 2外径MW 壁厚$((%计算内径+lm$((%i !i 2!!"!2/W 0!!4!!!2/W $!!)!&!1!!&"42!!2/!0"W 0&/!)!!!!0"W 4!2$!&2"0!&"1!!/"!$"W /!/"!!!$"W 1!00!&2!/!&"1/!4/!1"W /&/!$3!!!1"W 3!$2!&220!&"112""2""W $!11!!2""W !"!1"!&2)!!&"3!22/22/W 42!!!!2/"2/"W 4&/2)/!!24/21"W 1&/2$)!!)"")!/W 3&/23$!!)/")//W !"&3))0!!0""0""W !2)4$!!计算示例&)例*%已知流量;H !0.*h H "&"!0()*h #求管长.H )/""(#管径M 2""W $#轻工业部部标准B 8H!&"F B 9$!"J -*c (2%硬聚氯乙烯管的水头损失及平均水流速度!)解*%由表!$#2#!中查得外径M 2""((的塑料公称直径为M 82""((#又由表!$#2#0中查得M 82""((#当;H !0.*h 时#!"""Q H !&)0(#F H "&/(*h!因选用非标准管#故须对已求得的!"""Q 值加以修正!由表!$#2#!查得阻力修正系数i !H!&2)!#故实际水头损失为&,H Q i !.H !&)0!"""W !&2)!W)/""H /&44(同法查得流速修正值i 2H !&"3!#将由表!$#2#0中查得的流速F H "&/"(*h 加以修正!求得管内实际流速为FH "&/"W !&"3!H "&/0$(*h $0%工程中#塑料管一律用外径W 壁厚表示其规格!本计算表中公称管径是指外径而言#单位为毫米!三!水力计算塑料给水管水力计算见表!$#2#0!’/00!’第二章%塑料给水管水力计算’$00!’’400!’’100!’’300!’’"/0!’’!/0!’’2/0!’’)/0!’’0/0!’’//0!’’$/0!’第十六篇%管道水力计算’4/0!’第二章%塑料给水管水力计算’1/0!’第十六篇%管道水力计算’3/0!’第二章%塑料给水管水力计算’"$0!’第十六篇%管道水力计算第三章%钢筋混凝土圆管!非满流$R H "&"!0"水力计算一!计算公式;H FD $!$#)#!%图!$#)#!%,<M 2%%%%%F H !RX 2*)Q !*2$!$#)#2%式中%;...流量$()*h %(F...流速$(*h %(R...粗糙系数(X ...水力半径$(%(Q ...水力坡降(D ...水流断面$(%!当,<M 2时#DH $;#h Q R ;c a h ;%^2$!$#)#)%图!$#)#2%,<M2%%%%%3H 2;^$!$#)#0%3...湿周$(%!XH ;#h Q R ;c a h ;2;^$!$#)#/%当,[M 2时#DH $1#;I h Q R ;c a h ;%^2$!$#)#$%3H 2$1#;%^$!$#)#4%3...湿周$(%!XH 1#;I h Q R ;c a h ;2$1#;%^$!$#)#1%二!水力计算钢筋混凝土圆管MH !/">1""(($非满流#R H "&"!0%水力计算见表!$#)#!!表中;为流量$.*h %#F 为流速$(*h %!’!$0!’第三章%钢筋混凝土圆管!非满流$R H "&"!0"水力计算’2$0!’第十六篇%管道水力计算’)$0!’第三章%钢筋混凝土圆管!非满流$R H "&"!0"水力计算’0$0!’第十六篇%管道水力计算’/$0!’第三章%钢筋混凝土圆管!非满流$R H "&"!0"水力计算。


流量与管径、压力、流速的一般关系一般工程上计算时,水管路,压力常见为0.1--0.6MPa,水在水管中流速在1--3米/秒,常取1.5米/秒。
流量=管截面积X流速=0.002827X管内径的平方X流速(立方米/小时)。
其中,管内径单位:mm ,流速单位:米/秒,饱和蒸汽的公式与水相同,只是流速一般取20--40米/秒。
水头损失计算Chezy 公式这里:Q ——断面水流量(m3/s)C ——Chezy糙率系数(m1/2/s)A ——断面面积(m2)R ——水力半径(m)S ——水力坡度(m/m)根据需要也可以变换为其它表示方法:Darcy-Weisbach公式由于这里:h f——沿程水头损失(mm3/s)f ——Darcy-Weisbach水头损失系数(无量纲)l ——管道长度(m)d ——管道内径(mm)v ——管道流速(m/s)g ——重力加速度(m/s2)水力计算是输配水管道设计的核心,其实质就是在保证用户水量、水压安全的条件下,通过水力计算优化设计方案,选择合适的管材和确经济管径。
输配水管道水力计算包含沿程水头损失和局部水头损失,而局部水头损失一般仅为沿程水头损失的5~10%,因此本文主要研究、探讨管道沿程水头损失的计算方法。
1.1 管道常用沿程水头损失计算公式及适用条件管道沿程水头损失是水流摩阻做功消耗的能量,不同的水流流态,遵循不同的规律,计算方法也不一样。
输配水管道水流流态都处在紊流区,紊流区水流的阻力是水的粘滞力及水流速度与压强脉动的结果。
紊流又根据阻力特征划分为水力光滑区、过渡区、粗糙区。
管道沿程水头损失计算公式都有适用范围和条件,一般都以水流阻力特征区划分。
水流阻力特征区的判别方法,工程设计宜采用数值做为判别式,目前国内管道经常采用的沿程水头损失水力计算公式及相应的摩阻力系数,按照水流阻力特征区划分如表1。
沿程水头损失水力计算公式和摩阻系数表1达西公式是管道沿程水力计算基本公式,是一个半理论半经验的计算通式,它适用于流态的不同区间,其中摩阻系数λ可采用柯列布鲁克公式计算,克列布鲁克公式考虑的因素多,适用范围广泛,被认为紊流区λ的综合计算公式。


流量与管径、压力、流速的一般关系一般工程上计算时,水管路,压力常见为0.1--0.6MPa,水在水管中流速在1--3M/秒,常取1.5M/秒。
流量=管截面积X流速=0.002827X管内径的平方X流速(立方M/小时)。
其中,管内径单位:mm,流速单位:M/秒,饱和蒸汽的公式与水相同,只是流速一般取20--40M/秒。
水头损失计算Chezy公式Q = C-A-^[R~S这里:Q 断面水流量(m3/s)C ----- C hezy糙率系数(m1/2/s)A——断面面积(m2)R——水力半径(m)S 水力坡度(m/m)根据需要也可以变换为其它表示方法:Darcy-Weisbach 公式i = /. L—F 畑由于这里:h f 沿程水头损失(mm3/s)f ----- Darcy-Weisbach水头损失系数(无量纲)l ——管道长度(m)d ----- 管道内径(mm)v ----- 管道流速(m/s)g ----- 重力加速度(m/£)水力计算是输配水管道设计的核心,其实质就是在保证用户水量、水压安全的条件下,通过水力计算优化设计方案,选择合适的管材和确经济管径。
输配水管道水力计算包含沿程水头损失和局部水头损失,而局部水头损失一般仅为沿程水头损失的5〜10%,因此本文主要研究、探讨管道沿程水头损失的计算方法。
1.1管道常用沿程水头损失计算公式及适用条件管道沿程水头损失是水流摩阻做功消耗的能量,不同的水流流态,遵循不同的规律,计算方法也不一样。
输配水管道水流流态都处在紊流区,紊流区水流的阻力是水的粘滞力及水流速度与压强脉动的结果。
紊流又根据阻力特征划分为水力光滑区、过渡区、粗糙区。
管道沿程水头损失计算公式都有适用范围和条件,一般都以水流阻力特征区划分。
水流阻力特征区的判别方法,工程设计宜采用2数值做为判别式,目前国内管道经常采用的沿程水头损失水力计算公式及相应的摩阻力系数,按照水流阻力特征区划分如表1。
流量与管径、压力、流速的一般关系一般工程上计算时,水管路,压力常见为0.1--0.6MPa,水在水管中流速在1--3米/秒,常取1.5米/秒。
流量=管截面积X流速=0.002827X管内径的平方X流速(立方米/小时)。
其中,管内径单位:mm ,流速单位:米/秒,饱和蒸汽的公式与水相同,只是流速一般取20--40米/秒。
水头损失计算Chezy 公式这里:Q ——断面水流量(m3/s)C ——Chezy糙率系数(m1/2/s)A ——断面面积(m2)R ——水力半径(m)S ——水力坡度(m/m)根据需要也可以变换为其它表示方法:Darcy-Weisbach公式由于这里:h f——沿程水头损失(mm3/s)f ——Darcy-Weisbach水头损失系数(无量纲)l ——管道长度(m)d ——管道内径(mm)v ——管道流速(m/s)g ——重力加速度(m/s2)水力计算是输配水管道设计的核心,其实质就是在保证用户水量、水压安全的条件下,通过水力计算优化设计方案,选择合适的管材和确经济管径。
输配水管道水力计算包含沿程水头损失和局部水头损失,而局部水头损失一般仅为沿程水头损失的5~10%,因此本文主要研究、探讨管道沿程水头损失的计算方法。
1.1 管道常用沿程水头损失计算公式及适用条件管道沿程水头损失是水流摩阻做功消耗的能量,不同的水流流态,遵循不同的规律,计算方法也不一样。
输配水管道水流流态都处在紊流区,紊流区水流的阻力是水的粘滞力及水流速度与压强脉动的结果。
紊流又根据阻力特征划分为水力光滑区、过渡区、粗糙区。
管道沿程水头损失计算公式都有适用范围和条件,一般都以水流阻力特征区划分。
水流阻力特征区的判别方法,工程设计宜采用数值做为判别式,目前国内管道经常采用的沿程水头损失水力计算公式及相应的摩阻力系数,按照水流阻力特征区划分如表1。
沿程水头损失水力计算公式和摩阻系数表1达西公式是管道沿程水力计算基本公式,是一个半理论半经验的计算通式,它适用于流态的不同区间,其中摩阻系数λ可采用柯列布鲁克公式计算,克列布鲁克公式考虑的因素多,适用范围广泛,被认为紊流区λ的综合计算公式。
水电站、水利水电工程、压力管等水头压力的计算公式及参数一、工程压力单位:0.01mpa=1米水头(请参考下表)二、水电站有关装机、流量、水头经验公式电站装机容量W=集雨面积S×水头高H×0.3~0.5或W=设计流量Q×水头高H×7电站流量Q=装机容量W÷水头高H÷0.8电站引水洞径R半径=√Q÷(0.27~0.25)或R半径=√Q÷3.14÷2.7三、管径和流速计算、水头损失流量与管径、压力、流速的一般关系,一般工程上计算时,水管路,压力常见为0.1--0.6MPa,水在水管中流速在1--3米/秒,常取1.5米/秒。
流量=管截面积X流速=0.002827X管内径的平方X流速 (立方米/小时)。
其中,管内径单位:mm ,流速单位:米/秒,饱和蒸汽的公式与水相同,只是流速一般取20--40米/秒。
水头损失计算Chezy 公式Chezy这里:Q ——断面水流量(m3/s)C ——Chezy糙率系数(m1/2/s)A ——断面面积(m2)R ——水力半径(m)S ——水力坡度(m/m)根据需要也可以变换为其它表示方法:Darcy-Weisbach公式由于这里:hf ——沿程水头损失(mm3/s)f ——Darcy-Weisbach水头损失系数(无量纲)l ——管道长度(m)d ——管道内径(mm)v ——管道流速(m/s)g ——重力加速度(m/s2)水力计算是输配水管道设计的核心,其实质就是在保证用户水量、水压安全的条件下,通过水力计算优化设计方案,选择合适的管材和确经济管径。
输配水管道水力计算包含沿程水头损失和局部水头损失,而局部水头损失一般仅为沿程水头损失的5~10%,因此本文主要研究、探讨管道沿程水头损失的计算方法。
四、管道常用沿程水头损失计算公式及适用条件:管道沿程水头损失是水流摩阻做功消耗的能量,不同的水流流态,遵循不同的规律,计算方法也不一样。
流量与管径、压力、流速的一般关系一般工程上计算时,水管路,压力常有为 0.1--0.6MPa ,水在水管中流速在 1--3 米/ 秒,常取 1.5 米/ 秒。
流量 = 管截面积 X 流速 =0.002827X 管内径的平方 X 流速 (立方米 / 小时 )。
其中,管内径单位: mm ,流速单位:米 / 秒,饱和蒸汽的公式与水相同,可是流速一般取 20--40 米/ 秒。
水头损失计算 Chezy公式这里:Q——断面水流量(m3/s)C——Chezy糙率系数(m1/2/s)A——断面面积(m2)R——水力半径(m)S——水力坡度(m/m)依照需要也可以变换为其他表示方法 :Darcy-Weisbach公式由于这里:h f——沿程水头损失(mm3/s)f——Darcy-Weisbach水头损失系数(无量纲)l——管道长度(m)d——管道内径(mm)v——管道流速(m/s)g——重力加速度(m/s2)水力计算是输配水管道设计的核心,其实质就是在保证用户水量、水压安全的条件下,经过水力计算优化设计方案,选择合适的管材和确经济管径。
输配水管道水力计算包含沿程水头损失和局部水头损失,而局部水头损失一般仅为沿程水头损失的 5~10% ,因此本文主要研究、商议管道沿程水头损失的计算方法。
管道常用沿程水头损失计算公式及合用条件管道沿程水头损失是水流摩阻做功耗资的能量,不一样的水流流态,依照不一样的规律,计算方法也不一样样。
输配水管道.态都处在紊流区,紊流区水流的阻力是水的粘滞力及水流速度与压强脉动的结果。
紊流又依照阻力特色划分为水力圆滑区、过渡区、粗糙区。
管道沿程水头损失计算公式都有合用范围和条件,一般都以水流阻力特色区划分。
水流阻力特色区的鉴识方法,工程设计宜采用数值做为鉴识式,目前国内管道经常采用的沿程水头损失水力计算公式及相应的摩阻力系数,依照水流阻力特色区划分如表 1。
沿程水头损失水力计算公式和摩阻系数阻力特色合用条件水力公式、摩阻系数区水力圆滑>10区(1)紊流过渡 10<区<500(2)表 1符号意义雷诺数h:管道沿程水头损失v:平均流速d:管道内径γ:水的运动粘滞系数λ:沿程摩阻系数:管道当量粗糙度q:管道流量紊流粗糙>500Ch:海曾 -威廉系数区C:谢才系数R:水力半径n:粗糙系数i:水力坡降l:管道计算长度达西公式是管道沿程水力计算基本公式,是一个半理论半经验的计算通式,它合用于流态的不一样区间,其中摩阻系数λ可采用柯列布鲁克公式计算,克列布鲁克公式考虑的因素多,合用范围宽泛,被认为紊流区λ的综合计算公式。