大学物理 机械振动与机械波

机械振动机械波1. 引言机械振动和机械波是机械工程中重要的研究领域，它们在各个行业中都有广泛的应用。

机械振动研究的是物体在受到外力激励后产生的周期性运动，而机械波研究的是物体中能量传递的波动现象。

本文将介绍机械振动和机械波的基本概念、传播特性以及相关应用。

2. 机械振动2.1 振动的基本概念振动是物体围绕其平衡位置做周期性往复运动的现象。

物体在振动过程中会存在振幅、周期、频率等基本参数。

振幅表示振动的最大偏离量，周期表示振动一次所经历的时间，频率表示单位时间内振动的次数。

振动的基本参数可以通过物体的振动函数来描述。

2.2 单自由度振动系统单自由度振动系统是指只有一个自由度的振动系统，最简单的例子是弹簧振子。

弹簧振子由一个弹簧和一个质点组成，当质点受到外力激励时，会产生振动。

弹簧振子的振动可以用简谐振动来描述，简谐振动是一种最简单的周期性振动。

2.3 多自由度振动系统多自由度振动系统是指由多个自由度组成的振动系统，例如多个质点通过弹簧相互连接而成的系统。

多自由度振动系统的振动模式较为复杂，可以通过求解振动微分方程得到系统的振动模式和频率。

3. 机械波3.1 波动的基本概念波动是指能量传递在空间中传播的现象。

波动可以分为机械波和电磁波两大类，其中机械波是需要介质传播的波动现象。

机械波可以通过绳子上的波浪、水波以及地震波等来进行形象化理解。

3.2 机械波的分类根据振动方向和能量传播方向的不同，机械波可以分为横波和纵波两种。

横波是指振动方向垂直于能量传播方向的波动，例如绳子上的波浪；纵波是指振动方向和能量传播方向相同的波动，例如声波。

3.3 机械波的传播特性机械波的传播速度和频率有一定的关系，传播速度等于波动频率乘以波长。

波长是波动中一个完整波动周期所占据的距离。

不同介质中的机械波传播速度不同，波动传播过程中会发生折射、反射、衍射等现象。

4. 机械振动和机械波的应用机械振动和机械波在各个行业中都有广泛的应用。

衡水学院 理工科专业《大学物理B 》机械振动 机械波 习题解答命题教师：杜晶晶 试题审核人：杜鹏一、填空题（每空2分）1、一质点在x 轴上作简谐振动，振幅A ＝4cm ，周期T ＝2s ，其平衡位置取坐标原点。

若t ＝0时质点第一次通过x ＝－2cm 处且向x 轴负方向运动，则质点第二次通过x ＝－2cm 处的时刻为23s 。

2、一质点沿x 轴作简谐振动，振动范围的中心点为x 轴的原点，已知周期为T ，振幅为A 。

（a ）若t=0时质点过x=0处且朝x 轴正方向运动，则振动方程为cos(2//2)x A t T ππ=-。

（b ）若t=0时质点过x=A/2处且朝x 轴负方向运动，则振动方程为cos(2//3)x A t T ππ=+。

3、频率为100Hz ，传播速度为300m/s 的平面简谐波，波线上两点振动的相位差为π/3，则此两点相距 0.5 m 。

4、一横波的波动方程是))(4.0100(2sin 02.0SI x t y -=π，则振幅是 0.02m ，波长是 2.5m ，频率是 100 Hz 。

5、产生机械波的条件是有 波源 和 连续的介质 。

二、单项选择题（每小题2分）（C ）1、一质点作简谐振动的周期是T ,当由平衡位置向x 轴正方向运动时，从1/2最大位移处运动到最大位移处的这段路程所需的时间为（ ）（A ）T /12 （B ）T /8 （C ）T /6 （D ） T /4（ B ）2、两个同周期简谐振动曲线如图1所示，振动曲线1的相位比振动曲线2的相位（ ）图1（A ）落后2π （B ）超前2π （C ）落后π （D ）超前π （ C ）3、机械波的表达式是0.05cos(60.06)y t x ππ=+，式中y 和x 的单位是m ，t 的单位是s ，则（ ）（A ）波长为5m （B ）波速为10m ⋅s -1 （C ）周期为13s （D ）波沿x 正方向传播（ D ）4、如图2所示，两列波长为λ的相干波在p 点相遇。

机械振动机械波机械振动和机械波是物理学中重要的概念，涉及到了物体的振动和波动特性。

机械振动是指物体或系统在受到外界力的作用下发生的周期性或非周期性的振动运动，而机械波是指机械振动在介质中传播的能量传递过程。

机械振动有两个重要的参数，即振动周期和振幅。

振动周期是指一个完整的振动循环所需要的时间，通常用秒（s）表示。

振幅则是指振动的最大位移或最大速度，通常用米（m）来表示。

机械振动分为简谐振动和非简谐振动两种。

简谐振动是指当物体受到恢复力的作用后，其振动状态可以通过正弦或余弦函数来描述。

而非简谐振动则是指物体受到的恢复力不满足线性关系，振动状态无法通过简单的正弦或余弦函数来描述。

机械振动的运动可以通过振动方程来描述。

对于简谐振动而言，振动方程可以表示为x(t) = A * sin(ωt + φ)，其中x(t)是物体的位移，A是振幅，ω是角频率，t是时间，φ是相位差。

振动方程可以描述物体振动的位移、速度和加速度的关系，从而提供了对振动状态的全面了解。

机械波是机械振动在介质中传播的能量传递过程。

波动是由于介质中某一点的振动引起附近点的振动，从而传递能量。

机械波有两种主要类型，即横波和纵波。

横波是指波动的振动方向垂直于能量传播方向的波动，例如水波。

纵波则是指波动的振动方向与能量传播方向一致的波动，例如声波。

机械波的传播速度可以通过介质的性质和条件来确定。

对于弹性介质而言，传播速度可以表示为v = √(E/ρ)，其中v是波速，E是介质的杨氏模量，ρ是介质的密度。

不同介质的波速是不同的，比如在空气中，声速大约为343m/s，而在水中，水波的波速则约为1480m/s。

机械波的特性还包括波长和频率。

波长是指相邻两个振动峰或波谷之间的距离，通常用λ表示，单位是米。

频率是指在单位时间内波动中的相邻振动周期的个数，通常用赫兹（Hz）表示。

波长和频率之间有一个简单的关系，即v = λ * f，其中v是波速，λ是波长，f 是频率。

机械振动机械波一、选择题1．对一个作简谐振动的物体,下面哪种说法是正确的A 物体处在运动正方向的端点时,速度和加速度都达到最大值；B 物体位于平衡位置且向负方向运动时,速度和加速度都为零；C 物体位于平衡位置且向正方向运动时,速度最大,加速度为零；D 物体处在负方向的端点时,速度最大,加速度为零;2．质点作简谐振动,振动方程为)cos(φω+=t A x ,当时间2/T t =T 为周期时,质点的速度为A φωsin A v -=；B φωsin A v =；C φωcos A v-=； D φωcos A v =;3．一物体作简谐振动,振动方程为⎪⎭⎫ ⎝⎛+=4cos πωt A x ;在4T t =T 为周期时刻,物体的加速度为 A 2221ωA -； B 2221ωA ； C 2321ωA -； D 2321ωA ; 4．已知两个简谐振动曲线如图所示,1x 的位相比2x 的位相A 落后2π；B 超前2π； C 落后π； D 超前π;5．一质点沿x 轴作简谐振动,振动方程为⎪⎭⎫ ⎝⎛+⨯=-ππ312cos 1042t x SI ;从0=t 时刻起,到质点位置在cm x 2-=处,且向x 轴正方向运动的最短时间间隔为 A s 8/1； B s 4/1；C s 2/1；D s 3/1; 6．一个质点作简谐振动,振幅为A ,在起始时刻质点的位移为2/A ,且向x 轴的正方向运动,代表此简谐振动的旋转矢量图为7．一个简谐振动的振动曲线如图所示;此振动的周期为A s 12；B s 10；C s 14；D s 11;8．一简谐振动在某一瞬时处于平衡位置,此时它的能量是A 动能为零,势能最大；B 动能为零,机械能为零；C 动能最大,势能最大；D 动能最大,势能为零;9．一个弹簧振子做简谐振动,已知此振子势能的最大值为1600J;当振子处于最大位移的1/4时,此时的动能大小为A250J ； B750J ； C1500J ； D 1000J;10．当质点以频率ν作简谐振动时,它的动能的变化频率为 A ν； B ν2 ； C ν4； D2ν;11．一质点作简谐振动,已知振动周期为T,则其振动动能变化的周期是 AT ／4； BT/2； CT ； D2T;12．两个同振动方向、同频率、振幅均为A 的简谐振动合成后,振幅仍为A ,则这两个振动的相位差为A π/3；B π/3； C2π/3； D5π/6;xABC D)s21-13．已知一平面简谐波的波动方程为()bx at A y -=cos ,a 、b 为正值,则 A 波的频率为a ； B 波的传播速度为a b /； C 波长为b /π； D 波的周期为a /2π;14．一个波源作简谐振动,周期为,以它经过平衡位置向正方向运动时为计时起点,若此振动的振动状态以s m u 400=的速度沿直线向右传播;则此波的波动方程为A ⎥⎦⎤⎢⎣⎡+⎪⎭⎫ ⎝⎛-=23400200cos ππx t A y ； B ⎥⎦⎤⎢⎣⎡+⎪⎭⎫ ⎝⎛+=23400200cos ππx t A y ； C ⎥⎦⎤⎢⎣⎡+⎪⎭⎫ ⎝⎛+=2400200cos ππx t A y ； D ⎥⎦⎤⎢⎣⎡+⎪⎭⎫ ⎝⎛-=2400200cos ππx t A y ; 15．当波从一种介质进入另一种介质中时,下列哪个量是不变的 A 波长； B 频率； C 波速； D 不确定;16．一横波以速度u 沿x 轴负方向传播,t 时刻波形曲线如图所示,则该时刻 AA 点相位为π； BB 点静止不动； CC 点向下运动； DD 点向下运动;17．一简谐波沿x 轴正方向传播,4/T t =时的波形曲线如图所示;若振动以余弦函数表示,且此题各点振动的初相取π-到π之间的值,则 A 0点的初位相为00=φ；B1点的初位相为2/1πφ-=；C2点的初位相为πφ=2；D3点的初位相为2/3πφ-=;18．频率为Hz 100,传播速度为s m /300的平面简谐波,波线上两点振动的相位差为3/π,则此两点相距A m 2；B m 19.2；C m 5.0；D m 6.28;二、填空题1．一弹簧振子作简谐振动,振幅为A ,周期为T ,其运动方程用余弦函数表示;若0=t 时,uOYX1 2 3 4第题图1振子在负的最大位移处,则初位相为______________________； 2振子在平衡位置向正方向运动,则初位相为________________； 3振子在位移为2/A 处,且向负方向运动,则初位相为______; 2．一物体作余弦振动,振幅为m 21015-⨯,圆频率为16-sπ,初相为π5.0,则振动方程为=x ________________________SI ;3．一放置在水平桌面上的弹簧振子,振幅为A ,周期为T ;当0=t 时,物体在2/A x =处,且向负方向运动,则其运动方程为 ;4．一物体沿x 轴作简谐运动,振幅为cm 10,周期为s 0.4;当0=t 时物体的位移为cm x 0.50-=,且物体朝x 轴负方向运动;则s t 0.1=时,此物体的位移为 m ;5．一简谐运动曲线如图a 所示,图b 是其旋转矢量图,则此简谐振动的初相位为 ；s t 1=与0=t 的相位差φ∆= ；运动周期是 ;6．两列满足相干条件的机械波在空间相遇将发生干涉现象,其中相干条件包括：1频率_____________；2振动方向_____________和相差恒定; 7．两个同振动方向、同频率、振幅均为A 的简谐运动合成后,振幅仍为A ,则这两个简谐运动的相位差为___________; 8．同方向同频率振幅均为A ,相位差为2π的两个简谐运动叠加后,振幅为________;9．一个质点同时参与两个在同一直线上的简谐振动,其表达式分别为 ()6/2cos 10421π+⨯=-t x ,()6/52cos 10322π-⨯=-t x SI则其合成振动的振幅为___________,初相为_______________;10．两个同方向同频率的简谐振动,其合振动的振幅为cm 20,与第一个简谐振动的位相差为6/1πφφ=-;若第一个简谐振动的振幅为cm cm 3.17310=,则第二个简谐振动的振幅为__________cm ,第一、二两个简谐振动的位相差21φφ-为__________;11．一平面简谐波沿x 轴正方向传播,波速s m u /100=,0=t 时刻的波形曲线如图所示;波长=λ____________；12．惠更斯原理表明,介质中波动传播到的各点都可以看作是发射子波的波源,而在其后的任意时刻,这些子波的_______________就是新的波前; 包络包迹或包络面13．干涉型消声器结构原理如图所示,构可以消除噪声;达点A 时,分成两路而在点B 相遇,而相消;已知声波速度为s m /340,如果要消除频率为Hz 300的发动机排气噪声,则图中弯道与直管长度差至少应为____________;三、判断题1．对于给定的振动系统,周期或频率由振动系统本身的性质决定,而振幅和初相则由初始条件决定;2．对于一定的谐振子而言,振动周期与振幅大小无关; 3．简谐振动的能量与振幅的平方成正比;4．在简谐振动的过程中,谐振子的动能和势能是同相变化的; 5．两个同方向同频率简谐运动合成的结果必定是简谐运动;6．在简谐波传播过程中,沿传播方向相距半个波长的两点的振动速度必定大小相同,方向相反7．在平面简谐波传播的过程中,波程差和相位差的关系是21122x ∆=∆λπφ;8．频率相同、传播方向相同、相差恒定的两列波在空间相遇会发生干涉;第题图) 0-0。

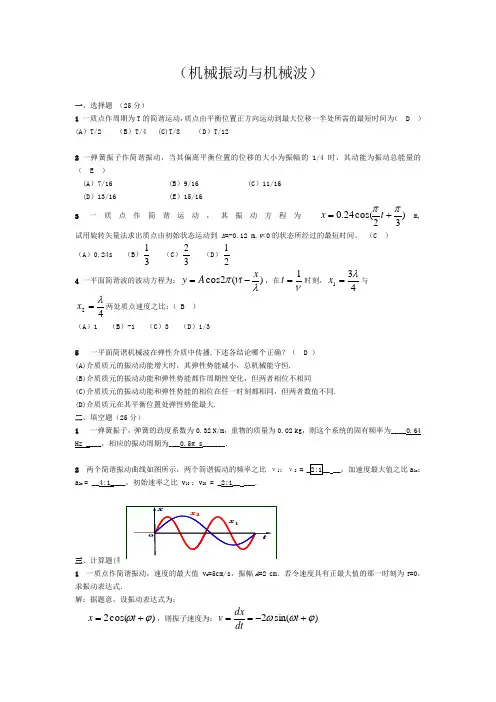
（机械振动与机械波）一、选择题 （25分）1 一质点作周期为T 的简谐运动，质点由平衡位置正方向运动到最大位移一半处所需的最短时间为（ D ） (A ）T/2 （B ）T/4 (C)T/8 （D ）T/122 一弹簧振子作简谐振动，当其偏离平衡位置的位移的大小为振幅的1/4时，其动能为振动总能量的（ E ）(A ）7/16 (B ）9/16 (C ）11/16 (D ）13/16 (E ）15/16 3一质点作简谐运动，其振动方程为)32cos(24.0ππ+=t x m,试用旋转矢量法求出质点由初始状态运动到 x =-0.12 m,v <0的状态所经过的最短时间。

（C ） （A ）0.24s （B ）31 （C ）32 （D ）214 一平面简谐波的波动方程为：)(2cos λνπx t A y -=，在ν1=t 时刻，431λ=x 与 42λ=x 两处质点速度之比：（ B ）（A ）1 （B ）-1 （C ）3 （D ）1/35 一平面简谐机械波在弹性介质中传播,下述各结论哪个正确？（ D ） (A)介质质元的振动动能增大时，其弹性势能减小，总机械能守恒. (B)介质质元的振动动能和弹性势能都作周期性变化，但两者相位不相同 (C)介质质元的振动动能和弹性势能的相位在任一时刻都相同，但两者数值不同. (D)介质质元在其平衡位置处弹性势能最大. 二、填空题（25分）1 一弹簧振子，弹簧的劲度系数为0.32 N/m ，重物的质量为0.02 kg ，则这个系统的固有频率为____0.64 Hz ____，相应的振动周期为___0.5π s______．2 两个简谐振动曲线如图所示，两个简谐振动的频率之比 ν1：ν2 = _2:1__ __，加速度最大值之比a 1m ：a 2m = __4:1____，初始速率之比 v 10 ：v 20 = _2:1__ ___.三、计算题(1 一质点作简谐振动，速度的最大值 v m =5cm/s ，振幅=2 cm ．若令速度具有正最大值的那一时刻为t =0，求振动表达式．解：据题意，设振动表达式为：)cos(2ϕω+=t x ，则振子速度为：)sin(2ϕωω+-==t dtdxvω2=m v ω=2.5 rad/s又因：速度正最大值的那个时刻是t=0，即，振子在平衡位置，沿着x 正向运动。

第十章 机械振动和机械波一、基本知识点机械振动：物体在平衡位置附近的往复运动叫做。

胡克定律: 弹簧弹性力F 的大小与位移x 的大小成正比，而且F 的方向与位移方向相反，即F kx =-式中，k 为弹簧的劲度系数。

具有这种性质的力称为线性回复力。

简谐振动的运动学方程:cos()x A t ωϕ=+式中A 为振幅，表示振动物体离开平衡位置的最大位移的绝对值；()t ωϕ+是决定简谐振动状态的物理量，称为在t 时刻振动的相位，单位是弧度()rad ；ϕ为初相位，是0t =时刻的相位；ω=角频率。

简谐振动的动力学方程:2220d x x dtω+=简谐振动的频率：振动物体在单位时间内完整振动的次数，单位是赫兹()Hz 。

简谐振动的周期：振动物体完成一次完整振动所经历的时间，单位是秒()s 。

关系：周期T 是频率ν的倒数；ω=2πν=2π/T简谐振动物体的速度:sin()cos()2dx A t A t dt πυωωϕωωϕ==-+=++ 简谐振动物体的加速度:22222cos()cos()d xa A t x A t dtωωϕωωωϕπ==-+=-=++振幅：A = 初相位：arctanx υϕω-= 式中，0x 为t=0时刻的初始位移，0υ为t=0s 时刻的初始速度。

旋转矢量法: 用一个旋转矢量末端在一条轴线上的投影点的运动来表示简谐振动的方法。

以简谐振动的平衡位置O 作为x 轴的坐标原点，自O 点出发作一矢量A（其长度等于简谐振动振幅A ）。

设0t = 时刻，矢量A 与x 轴所成的角等于初相位ϕ。

若矢量A以角速度ω（其大小等于简谐振动角频率ω）匀速绕O 点逆时针旋转，则在任一时刻矢量A末端在x 轴上的投影点P 相对原点的位移为cos()x A t ωϕ=+，显然，P 在x 轴上做简谐振动。

如图10-1所示。

cos()x A t ωϕ=+图10-1 简谐振动的旋转矢量法弹簧振子的弹性势能：222211cos ()22p E kx mA t ωωϕ==+弹簧振子的动能：222211sin ()22k E m mA t υωωϕ==+ 系统的总机械能：2212p k E E E mA ω=+=表明总机械能总量守恒。

衡水学院 理工科专业《大学物理B 》机械振动 机械波 习题解答命题教师：杜晶晶 试题审核人：杜鹏一、填空题（每空2分）1、一质点在x 轴上作简谐振动，振幅A ＝4cm ，周期T ＝2s ，其平衡位置取坐标原点。

若t ＝0时质点第一次通过x ＝－2cm 处且向x 轴负方向运动，则质点第二次通过x ＝－2cm 处的时刻为23s 。

2、一质点沿x 轴作简谐振动，振动范围的中心点为x 轴的原点，已知周期为T ，振幅为A 。

（a ）若t=0时质点过x=0处且朝x 轴正方向运动，则振动方程为cos(2//2)x A t T ππ=-。

（b ）若t=0时质点过x=A/2处且朝x 轴负方向运动，则振动方程为cos(2//3)x A t T ππ=+。

3、频率为100Hz ，传播速度为300m/s 的平面简谐波，波线上两点振动的相位差为π/3，则此两点相距 0.5 m 。

4、一横波的波动方程是))(4.0100(2sin 02.0SI x t y -=π，则振幅是 0.02m ，波长是 2.5m ，频率是 100 Hz 。

5、产生机械波的条件是有 波源 和 连续的介质 。

二、单项选择题（每小题2分）（C ）1、一质点作简谐振动的周期是T ,当由平衡位置向x 轴正方向运动时，从1/2最大位移处运动到最大位移处的这段路程所需的时间为（ ）（A ）T /12 （B ）T /8 （C ）T /6 （D ） T /4（ B ）2、两个同周期简谐振动曲线如图1所示，振动曲线1的相位比振动曲线2的相位（ ）图1（A ）落后2π （B ）超前2π （C ）落后π （D ）超前π （ C ）3、机械波的表达式是0.05cos(60.06)y t x ππ=+，式中y 和x 的单位是m ，t 的单位是s ，则（ ）（A ）波长为5m （B ）波速为10m ⋅s -1 （C ）周期为13s （D ）波沿x 正方向传播 （ D ）4、如图2所示，两列波长为λ的相干波在p 点相遇。

振 动 学 基 础内容提要一、振动的基本概念1、振动 某物理量随时间变化，如果其数值总在一有限范围内变动，就说该物理量在振动；2、周期振动 如果物理量在振动时，每隔一定的时间间隔其数值就重复一次，称为周期振动；3、机械振动 物体在一定的位置附近作往复运动称为机械振动；4、简谐振动 如果物体振动的位移随时间按余(正)弦函数规律变化，即：()0cos ϕω+=t A x这样振动称为简谐振动；5、周期T 物体进行一次完全振动所需的时间称为周期，单位：秒。

一次完全振动指物体由某一位置出发连续两次经过平衡位置又回到原来的状态。

6、振动频率ν 单位时间内振动的次数，单位：次/秒，称为赫兹〔Ｈz 〕；7、振动圆频率ω 振动频率的π2倍，单位是弧度/秒〔rad /s 〕，即Tππνω22== 8、振幅A 物体离开平衡位置〔0=x 〕的最大位移的绝对值； 9、相位ϕ0ϕωϕ+=t 称为相位或相，单位：弧()rad 。

它是时间的单值增函数，每经历一个周期T ，相位增加π2，完成一次振动； 10、初相位0ϕ 开始计时时刻的相位；11、振动速度v 表示振动物体位移快慢的物理量，即：()⎪⎭⎫ ⎝⎛++=+-==2cos sin 00πϕωωϕωωt A t A dt dx v 说明速度的相位比位移的相位超前2π； 12、振动加速度a 表示振动物体速度变化快慢的物理量，即：()()πϕωωϕωω++=+-===020222cos cos t A t A dtx d dt dv a加速度的相位比速度的相位超前2π，比位移的相位超前π； 13、初始条件 在0=t 时刻的运动状态〔位移和速度〕称为初始条件，它决定振动的振幅和初位相，即：⎪⎩⎪⎨⎧-======000000sin cos ϕωϕA v v A x x t t 则可求得： ⎪⎪⎩⎪⎪⎨⎧-=+=00022020x v tg v x A ωϕω二、旋转矢量法简谐振动可以用一旋转矢量在x 轴上的投影来表示。