大学物理A1机械振动

大学物理机械振动总结在物理学领域中，机械振动是指物体在受到外力作用后发生的周期性或非周期性的振动运动。

它是研究物体运动规律和能量传递的重要课题之一。

机械振动存在于我们日常生活的各个方面，从钟摆的摆动到汽车的悬挂系统，无处不体现着机械振动的存在。

首先，机械振动的基本特点是周期性。

在一个振动过程中，物体会在一定的时间间隔内不断重复同样的运动。

这种周期性运动可以用正弦函数或余弦函数来表达，而周期T则是振动的一个重要参数，表示一个完整振动过程所需要的时间。

其次，机械振动的频率是指单位时间内振动次数的多少。

频率f的倒数称为周期T，即T=1/f。

振动的频率越高，单位时间内振动次数越多，相应的周期也就越短。

频率与周期之间存在着倒数的关系，是彼此相互依存的。

频率和周期都是描述振动特征的重要参数，能够直观地表达出振动的快慢和紧凑程度。

再次，机械振动的振幅是指物体在振动过程中离开平衡位置的最大距离。

振幅越大，物体的运动范围也就越大，相应的振动能量也越大。

振幅与振动的能量之间存在着正相关的关系，振幅越大，能量传输的效果越明显。

此外，机械振动还有一个重要的参数叫做相位，用来描述物体在振动过程中的运动状态。

相位可以通过相位角来度量，它的变化范围在0到2π之间。

当相位角为0或2π时，物体达到最大振幅的正向运动；当相位角为π时，物体达到最大振幅的负向运动；当相位角为π/2或3π/2时，物体经过平衡位置，速度达到最大值。

机械振动的实际应用非常广泛。

例如，在建筑领域中，为了保证建筑物的稳定性和抗震性，需要对建筑结构进行振动分析和工程设计。

而在工业生产中，机械设备的振动也是一个重要的研究方向，可以通过合理的设计和调整来降低噪音和振动对设备和操作人员的影响。

此外，机械振动还有许多其他的应用，比如声学研究、航空航天技术等等。

总之，机械振动作为物理学领域中的一个重要分支，在科学研究和工程应用中都具有重要意义。

它的基本特征包括周期性、频率、振幅和相位等，这些特征参数可以用来描述和分析振动的规律和性质。

课程名称：大学物理授课班级：XX级XX班授课时间：2课时教学目标：1. 理解机械振动的概念，掌握简谐振动的特点。

2. 掌握机械振动的基本方程和运动规律。

3. 理解能量守恒原理在机械振动中的应用。

4. 能够分析简单的机械振动问题。

教学重点：1. 简谐振动的定义和特点。

2. 机械振动的基本方程和运动规律。

3. 能量守恒原理在机械振动中的应用。

教学难点：1. 简谐振动方程的推导和应用。

2. 能量守恒原理在复杂机械振动问题中的应用。

教学过程：第一课时一、导入1. 回顾初中物理中学过的振动和波的基本概念。

2. 提出问题：在物理学中，如何描述一个物体在平衡位置附近做周期性运动？二、新课讲解1. 机械振动的概念：物体在平衡位置附近做周期性运动的现象称为机械振动。

2. 简谐振动的定义和特点：- 定义：物体在回复力作用下，沿着某一方向做周期性运动。

- 特点：振动周期T与振幅A无关，振动方程具有正弦或余弦函数形式。

3. 简谐振动方程的推导：- 根据牛顿第二定律，推导简谐振动的微分方程。

- 解微分方程，得到简谐振动方程。

4. 机械振动的基本方程和运动规律：- 位置方程：x = A cos(ωt + φ)- 速度方程：v = -Aω sin(ωt + φ)- 加速度方程：a = -Aω^2 cos(ωt + φ)三、课堂练习1. 已知一个简谐振动的振幅为5cm，周期为4s，求该振动的频率和角频率。

2. 已知一个简谐振动的位置方程为x = 3cm cos(πt/2)，求该振动的速度和加速度。

四、小结1. 简谐振动的定义和特点。

2. 机械振动的基本方程和运动规律。

第二课时一、复习1. 回顾上节课所学内容，重点强调简谐振动的定义、特点、方程和运动规律。

二、新课讲解1. 能量守恒原理在机械振动中的应用：- 机械振动过程中，总能量保持不变。

- 机械能包括动能和势能，动能和势能之间可以相互转化。

2. 机械振动中能量守恒的推导：- 根据牛顿第二定律和简谐振动方程，推导机械振动中的能量守恒公式。

大学物理(第四版)课后习题及答案机械振动13 机械振动解答13-1 有一弹簧振子，振幅A=2.0×10-2m，周期T=1.0s，初相ϕ=3π/4。

试写出它的运动方程，并做出x--t图、v--t 图和a--t图。

13-1分析弹簧振子的振动是简谐运动。

振幅A、初相ϕ、角频率ω是简谐运动方程x=Acos(ωt+ϕ)的三个特征量。

求运动方程就要设法确定这三个物理量。

题中除A、ϕ已知外，ω可通过关系式ω=2π确定。

振子运动的速度T和加速度的计算仍与质点运动学中的计算方法相同。

解因ω=2π，则运动方程 T⎛2πt⎛x=Acos(ωt+ϕ)=Acos t+ϕ⎛⎛T⎛根据题中给出的数据得x=(2.0⨯10-2m)cos[(2πs-1)t+0.75π]振子的速度和加速度分别为v=dx/dt=-(4π⨯10-2m⋅s-1)sin[(2πs-1)t+0.75π] a=d2x/dt2=-(8π2⨯10-2m⋅s-1)cos[(2πs-1)t+0.75πx-t、v-t及a-t图如图13-l所示π⎛⎛13-2 若简谐运动方程为x=(0.01m)cos⎛(20πs-1)t+⎛，求：（1）振幅、频率、角频率、周期和4⎛⎛初相；（2）t=2s 时的位移、速度和加速度。

13-2分析可采用比较法求解。

将已知的简谐运动方程与简谐运动方程的一般形式x=Acos(ωt+ϕ)作比较，即可求得各特征量。

运用与上题相同的处理方法，写出位移、速度、加速度的表达式，代入t值后，即可求得结果。

解（l）将x=(0.10m)cos[(20πs-1)t+0.25π]与x=Acos(ωt+ϕ)比较后可得：振幅A= 0.10 m，角频率ω=20πs-1，初相ϕ=0.25π，则周期T=2π/ω=0.1s，频率ν=1/T=10Hz。

（2）t= 2s时的位移、速度、加速度分别为x=(0.10m)cos(40π+0.25π)=7.07⨯10-2m v=dx/dt=-(2πm⋅s-1)sin(40π+0.25π)a=d2x/dt2=-(40π2m⋅s-2)cos(40π+0.25π)13-3 设地球是一个半径为R的均匀球体，密度ρ5.5×103kg•m。

第四篇 振动与颠簸第十二章机械振动§ 12-1 简谐振动1、弹簧振子运动如图所取坐标，原点 O 在 m 均衡地点。

现将 m 略向右移到 A ，而后松开，此时，由于弹簧伸长而出现指向均衡地点的弹性力。

在弹性 力作用下，物体向左运动，当经过地点O 时，作用在 m 上弹性力等于 0，可是因为惯性作用， m 将持续向 O 左侧运动，使弹簧压缩。

此时，因为弹簧被压缩， 而出现了指向均衡地点的弹性力并将阻挡物体向左 运动，使 m 速率减小，直至物体静止于B （刹时静止），以后物体在弹性力作用下改变方向，向右运动。

这样在弹性力作用下物体左右来去运动，即作机械振动。

图 12-12、简谐振动运动方程由上剖析知， m 位移为 x （相对均衡点 O ）时，它遇到弹性力为（胡克定律） ：Fkx(12-1)式中： 当x即位移沿 +x 时，F 沿 -x ，即F0 当 x即位移沿 -x 时，F 沿+x ，即F 0k为弹簧的倔强系数， “—”号表示力 F 与位移 x （相对 O 点）反向。

定义：物体受力与位移正比反向时的振动称为简谐振动。

由定义知，弹簧振子做谐振动。

由牛顿第二定律知，m加快度为aF kxmm（ m为物体质量）ad 2 xd 2 x k x∵dt 2∴ dt2mk2∵ k、 m均大于 0，∴可令m可有：d 2 x2 x 0(12-2)dt 2式 (12-2) 是谐振动物体的微分方程。

它是一个常系数的齐次二阶的线性微分方程，它的解为x Asin t'(12-3)或x Acos t(12-4)'2式 (12-3)(12-4) 是简谐振动的运动方程。

所以，我们也能够说位移是时间t 的正弦或余弦函数的运动是简谐运动。

本书顶用余弦形式表示谐振动方程。

3、谐振动的速度和加快度物体位移：xAcos tdxAsin tV(12-5)速度：dtd 2 xa2 Acos t 2 x加快度：dt 2(12-6)可知：Vmax A amax 2 Ax t、V t 、 at 曲线以下图 12-2图 12-3第十二章机械振动沈阳工业大学郭连权（教授）说明：（1）Fkx 是谐振动的动力学特点；（2） a2 x是谐振动的运动学特点；（3）做谐振动的物体往常称为谐振子。

w w w .z h i n a n ch e.com《大学物理》AI 作业No No..01机械振动一、选择题1.把单摆从平衡位置拉开，使摆线与竖直方向成一微小角度θ，然后由静止放手任其振动，从放手时开始计时。

若用余弦函数表示其运动方程，则该单摆振动的初相位为[C ](A)θ;(B)23;(C)0;(D)π21。

解：t =0时，摆角处于正最大处，角位移最大，速度为零，用余弦函数表示角位移，0=ϕ。

2.轻弹簧上端固定，下系一质量为1m 的物体，稳定后在1m 下边又系一质量为2m 的物体，于是弹簧又伸长了x ∆。

若将2m 移去，并令其振动，则振动周期为[B](A)gm x m T 122∆=π(B)gm x m T 212∆=π(C)gm xm T 2121∆=π(D)()gm m x m T 2122+∆=π解：设弹簧劲度系数为k ，由题意，x k g m ∆⋅=2，所以xgm k ∆=2。

弹簧振子由弹簧和1m 组成，振动周期为gm xm k m T 21122∆==ππ。

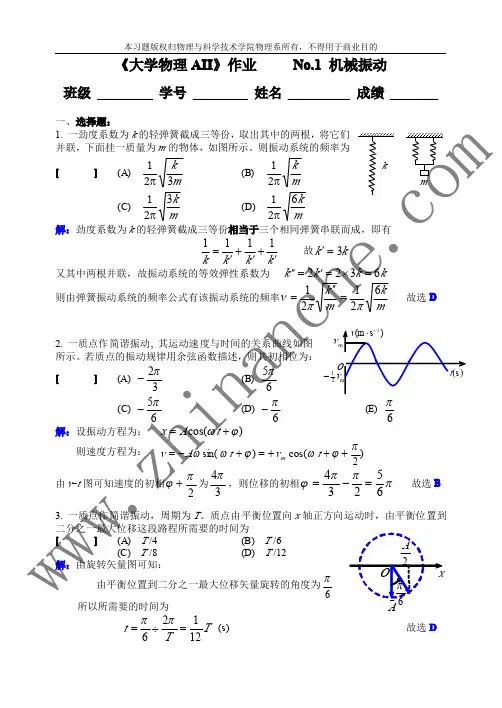
3.一劲度系数为k 的轻弹簧截成三等份，取出其中的两根，将它们并联在一起，下面挂一质量为m 的物体，如图所示。

则振动系统的频率为[B](A)m k π21(B)mk 621π(C)mk 321π(D)mk 321π解：每一等份弹簧的劲度系数k k 3=′，两等份再并联，等效劲度系数k k k 62=′=′′，所以振动频率mk m k 62121ππν=′′=4.一弹簧振子作简谐振动，总能量为1E ，如果简谐振动振幅增加为原来的两倍，重物的质量增加为原来的四倍，则它的总能量E 变为[D ](A)1E /4(B)1E /2(C)21E (D)41E 解：原来的弹簧振子的总能量212112112121A m kA E ω==，振动增加为122A A =，质量增加+w w w .z h i n a n ch e为124m m =，k 不变，角频率变为1122214ω===m k m k ，所以总能量变为()1212112121122222242142242121E A m A m A m E =⎟⎠⎞⎜⎝⎛=×⎟⎠⎞⎜⎝⎛××==ωωω5.一质点作简谐振动，周期为T 。

一、教学目标1. 知识目标：（1）理解机械振动的概念，掌握振动的分类和特点。

（2）掌握简谐振动的基本概念、特征量及其相互关系。

（3）掌握谐振动的能量、运动学特征和动力学特征。

（4）了解振动合成、频谱分析、阻尼振动和受迫振动等概念。

2. 能力目标：（1）能运用简谐振动的基本理论解决实际问题。

（2）能分析振动系统的稳定性，掌握振动控制方法。

3. 情感目标：（1）激发学生对物理学的兴趣，培养学生严谨的科学态度。

（2）培养学生团队合作精神，提高学生的综合素质。

二、教学内容1. 机械振动的概念及分类2. 简谐振动的基本概念、特征量及其相互关系3. 简谐振动的能量、运动学特征和动力学特征4. 振动合成5. 频谱分析6. 阻尼振动和受迫振动三、教学过程第一课时1. 导入新课通过生活中的实例，如钟摆、弹簧振子等，引入机械振动的概念。

2. 讲解机械振动的分类及特点（1）机械振动的分类：自由振动、受迫振动、阻尼振动。

（2）自由振动的特点：周期性、等幅性、能量守恒。

3. 讲解简谐振动的基本概念、特征量及其相互关系（1）简谐振动的定义：物体在平衡位置附近作等幅、周期性、有规律的往复运动。

（2）简谐振动的特征量：振幅、周期、频率、相位。

（3）特征量之间的关系：T = 2π/ω，f = 1/T。

4. 讲解简谐振动的能量、运动学特征和动力学特征（1）能量：动能和势能。

（2）运动学特征：速度、加速度。

（3）动力学特征：弹性力、恢复力。

第二课时1. 讲解振动合成（1）同方向同频率谐振动的合成：叠加原理。

（2）同方向不同频率谐振动的合成：矢量合成。

（3）相互垂直的两个振动的合成：平行四边形法则。

2. 讲解频谱分析（1）频谱的定义：将信号分解为不同频率的成分。

（2）频谱分析的方法：傅里叶变换。

3. 讲解阻尼振动和受迫振动（1）阻尼振动：系统受到阻力作用，能量逐渐耗散。

（2）受迫振动：系统受到外部周期性力的作用，产生振动。

第三课时1. 课堂小结回顾本节课所学内容，强调重点和难点。

⼤学物理习题A1（已选择）A1质点运动学⼀、选择题[ ]1、某质点作直线运动的运动学⽅程为x ＝6+3t -5t 3 (SI)，则点作A 、匀加速直线运动，加速度沿x 轴正⽅向．B 、匀加速直线运动，加速度沿x 轴负⽅向．C 、变加速直线运动，加速度沿x 轴正⽅向．D 、变加速直线运动，加速度沿x 轴负⽅向． [ ]2、⼀运动质点在某瞬时位于⽮径)(y x r ，的端点处, 其速度⼤⼩A 、dtdr B 、dt r d C 、dt r d || D 、22)()(dt dy dt dx +[ ]3、质点作曲线运动，r 表⽰位置⽮量，v 表⽰速度，a 表⽰加速度，S 表⽰路程，a t 表⽰切向加速度。

则下列表达式中(1)d /d t a =v ， (2)d /d r t =v ， (3)d /d S t =v ，(4)d /d t t a =v ．A 、只有(1)、(4)是对的B 、只有(2)、(4)是对的C 、只有(2)是对的D 、只有(3)是对的[ ]4、⼀质点在平⾯上作⼀般曲线运动，其瞬时速度为v ，瞬时速率v ，某⼀时间内的平均速度为v ，平均速率为v ，它们之间的关系必定有A 、 v v v,v ==B 、v v v,v =≠C 、 v v v,v ≠≠D 、 v v v,v ≠=[ ]5、质点作半径为R 的变速圆周运动时的加速度⼤⼩为(v 表⽰任⼀时刻质点的速率)A 、dt dvB 、Rv 2 C 、R v dt dv 2+ D 、 242)(Rv dt dv + [ ]6、关于曲线运动叙述错误的是 A 、有圆周运动的加速度都指向圆⼼B 、圆周运动的速率和⾓速度之间的关系是ωr v =C 、质点作曲线运动时，某点的速度⽅向就是沿该点曲线的切线⽅向D 、速度的⽅向⼀定与运动轨迹相切 [ ]7、以r 表⽰质点的位失， ?S 表⽰在?t 的时间内所通过的路程，质点在?t 时间内平均速度的⼤⼩为A 、t S ??;B 、t r ??C 、t r; D 、t r三、填空题1、已知质点的运动⽅程为26(34)r t i t j =++ (SI)，则该质点的轨道⽅程为；s t 4=时速度的⼤⼩。

大学物理学中的机械振动是指物体在受到外力作用后，产生周期性的来回振动运动的现象。

以下是关于机械振动的一些基本概念和内容：
1. 振动的基本特征
-周期性：振动是一个周期性的过程，即物体在围绕平衡位置来回振动。

-频率：振动的频率指的是单位时间内振动的周期数，通常用赫兹（Hz）表示。

-振幅：振动的振幅是物体从平衡位置最大偏离的距离。

2. 单自由度振动系统
-弹簧振子：是一种经典的单自由度振动系统，由弹簧和质点组成，受到弹簧的恢复力驱使质点振动。

-简谐振动：在没有阻尼和外力干扰的情况下，弹簧振子的振动是简谐的，即振动周期固定，频率与系统的固有频率相关。

3. 振动的参数和描述
-角频率：振动描述中常用的参数之一，表示振动的快慢程度，与频率之间有一定的关系。

-相位：描述振动状态的参数，表示振动的相对位置或状态。

-能量：振动系统具有动能和势能，能量在振动过程中不断转换，影响着振动的特性。

4. 阻尼振动和受迫振动
-阻尼振动：在振动系统中存在阻尼，会导致振动逐渐减弱，最终趋于稳定。

-受迫振动：当振动系统受到外力周期性作用时，会产生受迫振动，其频率与外力频率相同或有关。

5. 振动的应用
-工程领域：振动理论在工程领域有着广泛的应用，如建筑结构的抗震设计、机械系统的振动分析等。

-科学研究：振动理论也在物理学、工程学、生物学等领域中发挥重要作用，帮助解释和研究各种现象和问题。

以上是关于大学物理学中机械振动的一些基本内容和相关概念，希望能帮助您更好地理解这一领域的知识。

动contents •简谐振动•阻尼振动与受迫振动•振动的合成与分解•振动在介质中的传播•多自由度系统的振动•非线性振动与混沌目录01简谐振动简谐振动的定义与特点定义简谐振动是最基本、最简单的振动形式，指物体在跟偏离平衡位置的位移成正比，并且总是指向平衡位置的回复力的作用下的振动。

特点简谐振动的物体所受的回复力F与物体偏离平衡位置的位移x成正比，且方向始终指向平衡位置；振动过程中，系统的机械能守恒。

动力学方程根据牛顿第二定律，简谐振动的动力学方程可以表示为F=-kx，其中F为回复力，k为比例系数，x为物体偏离平衡位置的位移。

运动学方程简谐振动的运动学方程可以表示为x=Acos(ωt+φ)，其中A为振幅，ω为角频率，t为时间，φ为初相。

势能与动能在简谐振动过程中，系统的势能Ep和动能Ek都在不断变化，但它们的总和保持不变，即机械能守恒。

能量转换在振动过程中，势能和动能之间不断相互转换。

当物体向平衡位置运动时，势能减小、动能增加；当物体远离平衡位置时，势能增加、动能减小。

同方向同频率简谐振动的合成当两个同方向、同频率的简谐振动同时作用于同一物体时，它们的合振动仍然是一个简谐振动，其振幅等于两个分振动振幅的矢量和，其初相等于两个分振动初相的差。

同方向不同频率简谐振动的合成当两个同方向、不同频率的简谐振动同时作用于同一物体时，它们的合振动一般不再是简谐振动，而是比较复杂的周期性振动。

在某些特定条件下（如两个分振动的频率成简单整数比），合振动可能会呈现出一定的规律性。

相互垂直的简谐振动的合成当两个相互垂直的简谐振动同时作用于同一物体时，它们的合振动轨迹一般是一条复杂的曲线。

在某些特定条件下（如两个分振动的频率相同、相位差为90度），合振动轨迹可能会呈现出一定的规律性，如圆形、椭圆形等。

02阻尼振动与受迫振动阻尼振动的定义与分类定义阻尼振动是指振动系统在振动过程中，由于系统内部摩擦或外部介质阻力的存在，使振动幅度逐渐减小，能量逐渐耗散的振动。

习题7-1. 原长为m 5.0的弹簧，上端固定，下端挂一质量为kg 1.0的物体，当物体静止时，弹簧长为m 6.0．现将物体上推，使弹簧缩回到原长，然后放手，以放手时开始计时，取竖直向下为正向，写出振动式。

（g 取9.8）解：振动方程：cos()x A t ωϕ=+,在本题中，kx mg =，所以9.8k =；ω=== 振幅是物体离开平衡位置的最大距离，当弹簧升长为0.1m 时为物体的平衡位置，以向下为正方向。

所以如果使弹簧的初状态为原长，那么：A=0.1，当t=0时，x=-A ，那么就可以知道物体的初相位为π。

所以：0.1cos x π=+） 即)x =-7-2. 有一单摆，摆长m 0.1=l ，小球质量g 10=m .0=t 时，小球正好经过rad 06.0-=θ处，并以角速度rad/s 2.0=•θ向平衡位置运动。

设小球的运动可看作简谐振动，试求：（g 取9.8）（1）角频率、频率、周期；（2）用余弦函数形式写出小球的振动式。

解：振动方程：cos()x A t ωϕ=+ 我们只要按照题意找到对应的各项就行了。

（1）角频率： 3.13/rad s ω===，频率：0.5Hz ν=== ，周期：22T s π=== （2）根据初始条件：A θϕ=0cos可解得：32.2088.0-==ϕ，A所以得到振动方程：0.088cos 3.13 2.32t θ=-（）7-3. 一竖直悬挂的弹簧下端挂一物体，最初用手将物体在弹簧原长处托住，然后放手，此系统便上下振动起来，已知物体最低位置是初始位置下方cm 0.10处,求：（1）振动频率；（2）物体在初始位置下方cm 0.8处的速度大小。

解：（1）由题知 2A=10cm ，所以A=5cm ；1961058.92=⨯=∆=-x g m K 又ω=14196==m k ,即 （2）物体在初始位置下方cm 0.8处，对应着是x=3cm 的位置，所以：03cos 5x A ϕ== 那么此时的04sin 5v A ϕω=-=± 那么速度的大小为40.565v A ω== 7-4. 一质点沿x 轴作简谐振动，振幅为cm 12，周期为s 2。

大学物理机械振动 篇一：大学物理——机械振动 第十章 机械振动 基本要求 1．掌握简谐振动的基本概念和描述简谐振动的特征量的意义及相互关系。

2．掌握和熟练应用旋转 矢量法分析与解决有关简谐振动的问题。

3．掌握简谐振动的动力学与运动学特征，从而判定一个运动是否为简谐振动。

4．理解简谐振动的 能量特征，并能进行有关的计算。

5．理解两个同振动方向、同频率的简谐振动的合成。

6．了解同振动方向不同频率的简谐振动的合成和相互垂直的两个振动的合成。

7．了解频谱分析、阻尼振动与受迫振动。

8．了解混沌的概念和电磁振荡。

10-1 简谐振动 一． 弹簧振子 ?? f??kx１． 弹性力：2．运动学特征： dxdt 22 特征方程： 2 ??x?0 式中 ?2?K m 其解： x?Acos(?t??) 二． 描述谐振动的物理量 １． ２． 振幅：A 角频率：?? km ３． 频率：?? ? 2?2? ４． ５． ６． 三． 周期：T? ? 相位：?t?? 初相位：? 谐振动中的速度和加速度 v? dxdt??A?sin(?t??)?vmcos(?t??? ? 2 ) a? dvdt ? dxdt 2 2 ??A? 2 cos(?t??)?amcos(?t????) 四． 决定?,A,?的因素 1．? 决定于振动系统，与振动方式无关； 2．A,?决定于初始条件： v0 22 公式法: A?分析法： x0? 2 ? ，??arctg(? v0 ?x0 ) x0?Acos? ? cos?? x0Av0 ??1,?2 { ?0(1,2 象限）?0(3,4 象限） v0??Asin??sin??? 六．谐振动的能量 Ek? 1212mv 2 A? ? 1212 m?Asin(?t??)2 2 222 Ep? kx 2 ?kAcos(?t??)?12 12 12 m?Acos(?t??) 222 E?Ek?Ep? kA 2 ? ?Am 22 Ek? 1T ?0 T 12 m?Asin(?t??)dt? 222 14 mA? 22 ? 14 kA 2 Ep?Ek 例１． 已知 t?0 时 x0? 例２． 已知 t?0 时 x0?0,v0?0,求?思考： １． 地球， M,R 已知， 中间开一遂道； 小球 m， 从离表面 h 处掉入隧道， 问， 小球是否作谐振动？ ２． 复 摆问题（I,m,lc 已知） d?dt 22 A2,v0?0,求? ? mglI c ??0 ３． 弹簧串、并联 串联： 1k?1k1 ?1k2 并联：k?k1?k2 10-2 谐振动的旋转矢量表示法 一、幅矢量法 1. 2. 作 x 轴，O 为平衡位置； ? A 在 x 轴上的投影点 P 作谐振动： x?Acos(?t??) 3. T? O ? A 以角速度?旋转一周，P 正好来回一次： 2? P P0 ? 二、参考圆法 1. 2.三、相位差 1. 同频率、同方向的两谐振动的相位差就是它们的初相差，即：????2??1 2. 超前与落后 例 1. 一物体沿 x 轴作简谐振动，振幅 A?12cm，周期 T?2s，t?0 时，位移为 6cm 且向 x 正方向运动，求： 1) 初位相及振动方程； 2) t?0.5s 时，物体的位置、速度和加速度； 3) x0??6cm 处，向 x 轴负方向运动时，物体的速度和加速度，以及从这一位置回到平衡位置所需的最 短时间； 例 2. 设有一音叉的振动为谐振动，角频率为??6.28?10s 2 ?1 以 O 为原点，A 为半径作圆，x 轴； 在图上根据已知求未知 ，音叉尖端的 振幅 A?1mm。

N O1机械振动答案本页仅作为文档封面，使用时可以删除This document is for reference only-rar21year.March《大学物理AII 》作业 机械振动一、选择题：1．假设一电梯室正在自由下落，电梯室天花板下悬一单摆(摆球质量为m ，摆长为l ) 。

若使单摆摆球带正电荷，电梯室地板上均匀分布负电荷，那么摆球受到方向向下的恒定电场力F 。

则此单摆在该电梯室内作小角度摆动的周期为：[ C ] (A) Fm l π2 (B) Flmπ2(C) Fmlπ2 (D) mlF π2 解： 2．图(a)、(b)、(c)为三个不同的简谐振动系统。

组成各系统的各弹簧的原长、各弹簧的劲度系数及重物质量均相同。

(a)、(b)、(c)三个振动系统的2（为固有角频率）值之比为[ B ] (A) 2∶1∶21(B)1∶2∶4(C) 2∶2∶1 (D) 1∶1∶2解：由弹簧的串、并联特征有三个简谐振动系统的等效弹性系数分别为：2k，k ，k 2 则由m k=2ω可得三个振动系统的2（为固有角频率）值之比为：m k 2 ：m k ：m k2，即1∶2∶4 故选B 3．两个同周期简谐振动曲线如图所示。

则x 1的相位比x 2的相位 [ A ] (A) 超前/2 (B) 落后 (C) 落后 解：由振动曲线画出旋转矢量图可知x 1的相位比x 2的相位超前k m m mk k k k (b) (c) t x O x 1 x 2x 2A1A ω4．一物体作简谐振动，振动方程为)21cos(π+=t A x ω。

则该物体在t = T /8（T 为振动周期）时刻的动能与t = 0时刻的动能之比为： [ B ] (A) 1:4 (B) 1:2 (C) 1:1 (D) 2:1 (E) 4:1解：由简谐振动系统的动能公式：)21(sin 2122πω+=t kA E k有t = 0时刻的动能为：22221)2102(sin 21kA T kA =+⋅ππt = T /8时刻的动能为：22241)2182(sin 21kA T T kA =+⋅ππ，则在t = T /8时刻的动能与t = 0时刻的动能之比为：1:2二、填空题：1．用40N 的力拉一轻弹簧，可使其伸长10cm 。

《大学物理A Ⅰ》机械振动习题、答案及解法2010一、 选择题1.下列四种运动（忽略阻力）中哪一种是简谐振动？（C ）(A)小球在地面上作完全弹性的上下跳动(B)细线悬挂一小球在竖直平面上作大角度的来回摆动(C)浮在水里的一均匀矩形木块，将它部分按入水中，然后松开，使木块上下浮动 (D)浮在水里的一均匀球形木块，将它部分按入水中，然后松开，使木块上下浮动 参考答案：A 中小球没有受到回复力的作用；B 中由于是大角度，所以θ与θsin 不能近似相等，不能看做简谐振动； D 中球形木块所受力F 与位移x 不成线性关系，故不是简谐振动。

2.如图1所示，以向右为正方向，用向左的力压缩一弹簧，然后松手任其振动，若从松手时开始计时，则该弹簧振子的初相位为（D ）(A) 0 (B) 2π (C)2π-(D) π 参考答案：0=t A x -=0 00〉v 则πϕ=3.一质量为m 的物体挂在劲度系数为k 的轻弹簧下面，其振动周期为T 。

若将此轻弹簧分割成三等份，将一质量为m 2的物体挂在分割后的一根弹簧上，则此弹簧振子的周期应为（B ）(A)T 63 (B)T 36 (C)T2 (D)T 6参考答案：km T π2=T k m T 36322=='π4.两相同的轻弹簧各系一物体（质量分别为1m 、2m ）作简谐振动（振幅分别为1A 、2A ），问下列哪一种情况两振动周期不同（B ） （A ）上振动动，另一个在竖直方向一个在光滑水平面上振、,2121A A m m == （B ）作水平振动两个都在光滑的平面上、,222121A A m m == （C ）作水平振动两个都在光滑的平面上、,22121A A m m ==（D ）竖直振动动，另一个在月球上作一个在地球上作竖直振、,2121A A m m ==参考答案：因为kmT π2= 与振幅无关故答案为B5.一个质点做简谐振动，已知质点由平衡位置运动到二分之一最大位移处所需要的最短时间为0t ，则该质点的振动周期T 应为［B ］(A)04t (B) 012t (C) 06t (D) 08t参考答案：()2sin A t A =ω 6320πππω=-=t 06t πω=0012622t t T ===ππωπ6.已知月球上的重力加速度是地球的61，若一个单摆(只考虑小角度摆动)在地球上的振动周期为T ，将该单摆拿到月球上去，其振动周期应为（C ） (A)T 6 (B)6T (C)T 6 (D)6T参考答案：gl T π20= 单摆拿到月球上，062662T g l g l T =⋅==ππ7.一简谐振动的旋转矢量图如图2所示，设图中圆的半径为R ，则该简谐振动的振动方程为（A ） (A)⎪⎭⎫ ⎝⎛+=4cos ππt R x(B) ⎪⎭⎫ ⎝⎛+=4sin ππt R x(C)⎪⎭⎫ ⎝⎛-=4cos ππt R x (D) ⎪⎭⎫ ⎝⎛+=42cos ππt R x参考答案： 由图知，初相为4π，在t 之间内转过t π， 0=t A x 220= 00〈v 则 4πϕ= 8.已知某简谐振动的振动曲线如图3所示，位移的单位为米，时间单位为秒，则此简谐振动的振动方程为（C ） (A)()SI 322411cos 10⎪⎭⎫ ⎝⎛+=ππt x(B)()SI 67247cos 10⎪⎭⎫ ⎝⎛-=ππt x(C)()SI 32247cos 10⎪⎭⎫ ⎝⎛-=ππt x(D) ()SI 322411cos 10⎪⎭⎫ ⎝⎛-=ππt x参考答案：由图知，振幅m 10=A ，0=t 20A x -= 00〉v 向正向运动则 32πϕ-=9.某弹簧振子的振动曲线如图4所示，则由图可确定s 2=t 时，振子的速66-度为（A ） (A) 1s m 3-⋅π (B) 1s m 3-⋅-π(C)1s m 3-⋅ (D) 1s m 3-⋅-参考答案：)22cos(6ππ+=t x)22sin(3πππ+-=t v)s m (3)23sin(3)2(1-⋅=-=πππv10.一质量为m 的物体与一个劲度系数为k 的轻弹簧组成弹簧振子，当其振幅为A 时，该弹簧振子的总能量为E 。