一维波动方程的达郎贝尔公式
- 格式:doc
- 大小:186.50 KB
- 文档页数:7


一维波动方程的达郎贝尔公式1达郎贝尔公式在常微分方程的定解问题中,通常是先求方程的通解,然后利用定解条件确定通解所含的任意常数,从而得到定解问题的解。
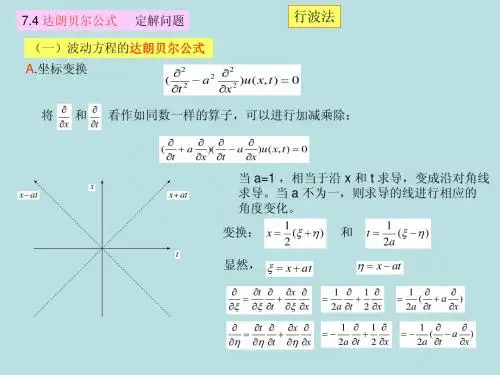
考虑无限长弦的自由振动问题⎪⎪⎩⎪⎪⎨⎧=∂∂=>+∞<<∞-∂∂=∂∂==)(|),(|0, ,0022222x tu x u t x xu a t u t t φϕ ① 作自变量的代换⎩⎨⎧-=+=atx atx ηξ 利用复合函数的微分法有:ηξ∂∂-∂∂=∂∂uau a t u )2(22222222ηηξξ∂∂+∂∂∂-∂∂=∂∂u u u a t u 同理有:22222222ηηξξ∂∂+∂∂∂+∂∂=∂∂uu u x u 将①化为:02=∂∂∂ηξu并将它两端对η进行积分得:)(0ξξf u=∂∂ 其中)(0ξf 是ξ的任意函数,再将此式对ξ积分)()()()(),(2120ηξηξξf f f d f t x u +=+=⎰=)()(21at x f at x f -++ ②其中21f f 、是任意两次连线可微函数,式②即为方程①的含有两个任意函数的通解。
由初始条件可得:)()()(21x x f x f ϕ=+)()()(2''1x x f x af φ=+通过积分可得:⎰+-+-++=atx at x d aat x at x t x u ξξϕφϕ)(21)]()([21),(称此式为一维波动方程的达郎贝尔公式。
2解的物理意义由于波动方程的通解是两部分)(1at x f +与)(2at x f -。
)(22at x f u -=表示了以速度a 向x 轴正方向传播的行波,称为右行波。
同理,)(11at x f u +=表示了以速度a 向x 轴负方向传播的行波,称为左行波。
由达郎贝尔公式,解在点),(t x 的值由初始条件在区间],[at x at x +-内的值决定,称区间],[at x at x +-为点),(t x 的依赖区域,在t x-平面上,它可看作是过点),(t x ,斜率分别a1± 为的两条直线在x 轴上截得的区间。

常微分方程的达朗贝尔公式和Green公式常微分方程(Ordinary Differential Equations, ODEs)是数学的一个分支,研究的是只依赖于一维自变量的函数和它们的导数。
常微分方程是各个领域中最重要的数学工具之一,广泛应用于物理、工程、经济和生物等领域。
在解常微分方程时,达朗贝尔公式和Green公式是两个非常重要的公式。
本文将对它们的定义、性质和应用进行详细介绍。
达朗贝尔公式达朗贝尔公式(D'Alembert's formula)是解一维波动方程(Wave Equation)的经典公式。
一维波动方程是描述一维波动传播的方程,形式为:$$\frac{\partial^2 u}{\partial t^2}=c^2\frac{\partial^2 u}{\partial x^2}$$其中,$u(x,t)$是波函数,$c$是波速,$x$和$t$分别表示空间和时间。
由于常微分方程只有一个自变量,因此我们需要对时间或空间变量进行临时的剖分才能解决这类方程。
达朗贝尔公式给出了波函数在任意时刻和任意位置的解析表达式,形式为:$$u(x,t)=\frac{1}{2}[f(x+ct)+f(x-ct)]+\frac{1}{2c}\int_{x-ct}^{x+ct}g(y)dy$$其中,$f(x)$是初始波形(Initial Waveform),$g(x)$是初始速度(Initial Velocity),$c$是波速。
这个公式的第一项表示波源在$t=0$时刻释放的波形在$x$处的振幅随时间的变化,第二项表示波源在$t=0$时刻释放的波速在$x$处的振幅随时间的变化。
达朗贝尔公式的一个重要性质是线性叠加性。
如果有多个波源在不同位置、不同时刻释放波形和波速,那么它们的叠加波形可以通过将它们对应的达朗贝尔公式相加而得到。
这样,我们就可以用达朗贝尔公式求解复杂的波动问题。
Green公式Green公式(Green's formula)是解各种常微分方程的一个通用技巧。







波动方程的达朗贝尔公式达朗贝尔公式是描述波动方程解的一种常见方法,它是由法国天文学家和数学家达朗贝尔于1787年提出的。
在描述一维波动问题时,达朗贝尔公式可以非常有效地解决问题。
首先,我们来看一维波动方程的基本形式:∂²u/∂t²=v²∂²u/∂x²其中u(x,t)表示波的位移,v表示波速,x表示空间坐标,t表示时间。
利用达朗贝尔公式,我们可以将一维波动方程的解表示为:u(x,t) = f(x+vt) + g(x-vt)其中f(x)和g(x)是任意两个可微函数。
达朗贝尔公式的推导可以通过变量分离法得到。
首先,我们将u(x,t)表示为两个变量的函数u(x,t)=F(x)G(t),然后将其代入波动方程:F''(x)G(t)=v²F(x)G''(t)两边除以v²FG,得到:F''(x)/F(x)=G''(t)/G(t)等式左边只依赖于x,右边只依赖于t,所以两边都等于一个常数k²:F''(x)/F(x)=G''(t)/G(t)=k²然后我们分别解这两个常微分方程。
对于F''(x)/F(x)=k²,我们可以得到解:F(x) = A e^(kx) + B e^(-kx)对于G''(t)/G(t)=k²,我们可以得到解:G(t) = C e^(ikt) + D e^(-ikt)其中A、B、C和D为任意常数,i为虚数单位。
因此u(x,t) = F(x)G(t) = [A e^(kx) + B e^(-kx)][C e^(ikt) + De^(-ikt)]我们可以通过组合常数A、B、C和D得到f(x)和g(x)。
根据指数函数的性质,我们可以将解写成达朗贝尔公式的形式:u(x,t) = f(x+vt) + g(x-vt)其中f(x+vt) = (A e^(kx) + B e^(-kx)) (C e^(ikt) + D e^(-ikt))g(x-vt) = (A e^(kx) + B e^(-kx)) (C e^(ikt) + D e^(-ikt))达朗贝尔公式的形式表明,波动方程的解可以表示为由两个运动方向相反的平面波的叠加形式。
一维波动方程可用如下的方式推导:一列质量为m的小质点,相邻质点间用长度h的弹簧连接。
弹簧的劲度系数(又称“倔强系数”)为k:
其中u(x) 表示位于x的质点偏离平衡位置的距离。
施加在位于x+h处的质点m上的力为:
其中代表根据牛顿第二定律计算的质点惯性力,代表根据
胡克定律计算的弹簧作用力。
所以根据分析力学中的达朗贝尔原理,位于x+h处质点的运动方程为:
式中已注明u(x) 是时间t的显函数。
若N个质点间隔均匀地固定在长度L = N h的弹簧链上,总质量M = N m,链的总体劲度系数为K = k/N,我们可以将上面的方程写为:
取极限N, h就得到这个系统的波动方程:
在这个例子中,波速。
一维波动方程的达郎贝尔公式∂²ψ/∂t²=v²∂²ψ/∂x²其中,ψ表示波函数,t表示时间,x表示位置,v表示波速。
这个方程是一个偏微分方程,描述了波函数随时间和位置的变化。
解决这个方程是一个经典的物理问题,在过去的几个世纪中,许多科学家对此进行了研究。
达郎贝尔公式是一维波动方程的特解,可以表示为:ψ(x, t) = f(x + vt) + g(x - vt)其中,f和g是任意可微函数,表示波函数的初始形态和初始速度分布。
达郎贝尔公式的形式很简单,实际上是波方程的一般解的特例。
它可以表示波函数在任意时刻和位置的值。
在达郎贝尔公式中,ψ(x,t)的值等于两个波的叠加,一个波向右传播,一个波向左传播,它们的速度都是v。
达郎贝尔公式的物理意义非常重要。
它说明了波函数是由两个波的叠加形成的。
一个波向右传播,一个波向左传播。
两个波的传播速度相同,但方向相反。
这种叠加能够形成各种形状的波,可以是周期性的波、不规则形状的波或波包等。
达郎贝尔公式还可以进一步推广到波包的情况。
波包可以近似地看作是一组不同波长的波的叠加,可以用来描述复杂波动现象。
波包的传播速度可以通过对波包进行傅里叶变换得到。
除了达郎贝尔公式,还有其他方法可以求解一维波动方程。
例如,可以使用傅里叶变换将波动方程转化为频域方程,然后通过求解频域方程得到波函数。
此外,也可以使用有限差分法和有限元法等数值方法来求解波动方程。
总之,一维波动方程的达郎贝尔公式是一种简单而重要的解法,可以用来计算波的传播情况。
它描述了波函数在任意时刻和位置的值,可以用来分析各种波动现象的特性和行为。
通过研究和理解达郎贝尔公式,可以深入理解一维波动方程及其在物理学中的应用。
第四章 行波法
一 一维波动方程的达郎贝尔公式 1达郎贝尔公式
在常微分方程的定解问题中,通常是先求方程的通解,然后利用定解条件确定通解所含的任意常数,从而得到定解问题的解。
考虑无限长弦的自由振动问题
⎪⎪⎩⎪⎪⎨
⎧=∂∂=>+∞<<∞-∂∂=∂∂==)
(|),(|0, ,0
022
2
22x t
u x u t x x
u a t u t t φϕ ① 作自变量的代换
⎩⎨
⎧-=+=at
x at
x ηξ 利用复合函数的微分法有:
η
ξ∂∂-∂∂=∂∂u
a
u a t u )2(22
2222
22η
ηξξ∂∂+∂∂∂-∂∂=∂∂u u u a t u
同理有:2
2222222ηηξξ∂∂+∂∂∂+∂∂=∂∂u
u u x u 将①化为:02=∂∂∂η
ξu
并将它两端对η进行积分得:
)(0ξξ
f u
=∂∂ 其中)(0ξf 是ξ的任意函数,再将此式对ξ积分
)()()()(),(2120ηξηξξf f f d f t x u +=+=⎰
=
)()(21at x f at x f -++ ②
其中21f f 、是任意两次连线可微函数,式②即为方程①的含有两个任意函数的通解。
由初始条件可得:
)()()(21x x f x f ϕ=+ )()()(2''
1x x f x af φ=+
通过积分可得:
⎰+-+-++=at
x at x d a
at x at x t x u ξξϕφϕ)(21)]()([21),(
称此式为一维波动方程的达郎贝尔公式。
2解的物理意义
由于波动方程的通解是两部分)(1at x f +与)(2at x f -。
)(22at x f u -=表示了以速度a 向x 轴正方向传播的行波,称
为右行波。
同理,)(11at x f u +=表示了以速度a 向x 轴负方向传播的行波,称为左行波。
由达郎贝尔公式,解在点),(t x 的值由初始条件在区间],[at x at x +-内的值决定,称区间],[at x at x +-为点),(t x 的
依赖区域,在t x -平面上,它可看作是过点),(t x ,斜率分
别a
1
± 为的两条直线在x 轴上截得的区间。
这里要掌握半无限长弦的自由振动问题和一维非齐次波动方程的柯西问题的解。
3 半限长弦的自由振动问题 定解问题
⎪⎪⎩
⎪
⎪⎨⎧=∂∂==>>∂∂=∂∂===)
10.4()(|),(|)9.4(0|)8.40,000022
2
22
(
, x t u
x u u x t x u a t u t x x φϕ 用延拓法求解,注意边界条件(4.9),采用奇延拓。
令
⎩⎨⎧<--≥=Φ 0),(0,)()(x x x x x ϕϕ
⎩⎨⎧<--≥=ψ
0),(0,)()(x x x x x φφ
考虑定解问题
⎪⎪⎩⎪⎪⎨
⎧ψ=∂∂Φ=>+∞<<∞-∂∂=∂∂== , )(|),(|0,0022
2
22x t
u x u t x x
u a t u t x 它的解可由达郎贝尔公式得:
⎰+-ψ+-Φ++Φ=at
x at x d a
at x at x t x U ξξ)(21)]()([21),(。
4 一维非齐次波动方程的柯西问题
定解问题
⎪⎪⎩⎪⎪⎨
⎧=∂∂=>+∞<<∞-+∂∂=∂∂==)12.4()(|),(|)11.4(0,),(0022
2
22 , x t
u x u t x t x f x
u a t u t x φϕ 令),(),(),(t x V t x U t x u +=,可将此定解分解成下面两个定解问题:
(I) ⎪⎪⎩⎪⎪⎨⎧=∂∂=>+∞<<∞-∂∂=∂∂== , )(|),(|0,00222
22x t u x u t x x
u a t u t x φϕ
(II) ⎪⎪⎩⎪⎪⎨⎧=∂∂=>+∞<<∞-+∂∂=∂∂== , 0|,0|0,),(0022
2
22t x t
u u t x t x f x
u a t u
其中问题(I)的解可由达朗贝尔公式给出: ⎰+-+-++=at
x at x d a
at x at x t x U ξξϕϕϕ)(21)]()([21),(。
对于问题(II),有下面重要的定理。
定理(齐次化原理)设),,(τωt x 是柯西问题
⎪⎪⎩⎪⎪⎨
⎧=∂∂=>∂∂=∂∂== , ),(|,0|22
2
22τωωτωωττx f t
t x
a t t x 的解)0(≥τ,则⎰=t
d t x t x V 0),,(),(ττω是问题(II)的解。
二 三维波动方程的柯西问题 1 三维波动方程的泊松公式 考
虑
三
维
波
动
方
程
的
柯
西
问
题
⎪⎪⎩⎪⎪⎨
⎧=∂∂=>+∞<<∞-∂∂+∂∂+∂∂=∂∂==)18.4(),,(|),,,(| 4.17(0,,, )(0022
22222
22 ) z y x t
u z y x u t z y x z u y u x u a t
u t t φϕ (1)三维波动方程的球对称解
如果将三维波动方程的空间坐标用球坐标表示,则波动方程化为:
2222
222sin 1)(sin sin 1)(1ϕ
θθθθ∂∂+∂∂+∂∂∂∂u
r u r r u r r r = ) (19.412
22t
u
a ∂∂ 如果波函数u 与θ,ϕ变量无关,而只与变量t r ,有关,即
u 是所谓球对称的,这时式可简化为:
)(122
r u r r r ∂∂∂∂=2221t
u
a ∂∂ )2(222
2
2r u r u r a t u ∂∂+∂∂=∂∂ 即有:2
2
2
22)()(r
ru a t ru ∂∂=∂∂。
这是关于的一维波动方程,其通解为:
)()(),(21at r f at r f t r ru -++=
从而)]()([1
),(21at r f at r f r
t r ru -++=即得到三维波动方程
关于原点为球对称的解。
(2)三维波动方程的泊松公式
⎪⎪⎩⎪⎪⎨
⎧=∂∂=>+∞<<∞-∂∂+∂∂+∂∂=∂∂==)18.4(),,(|),,,(| 4.17(0,,, )(00222222
222 ) z y x t
u z y x u t z y x z u y u x u a t
u t t φϕ 的解为:
=),,,(t z y x u t a ∂∂π41ds at M
at
S ⎰⎰),,(ζηξϕ+a π41ds at M at
S
⎰⎰
),,(ζηξϕ,称它为三维波动方程柯西问题的泊松公式。
这里要求掌握三维波动方程柯西问题的泊松公式的推导过程。
2降维法
利用三维波动方程柯西问题的泊松公式来导出二维波动方程柯西问题的解。
这种利用高维问题的解推导低维问题的方法称之为降维法。
二维波动方程的柯西的问题:
⎪⎪⎩⎪⎪⎨
⎧=∂∂=>+∞<<∞-∂∂+∂∂=∂∂==)
,(|),,(|0,,, )(0
022
222
22y x t
u y x u t z y x y u x u a t
u t t φϕ
令),,(),,(_
z y x u z y x u =,将上式的解视为特殊的三维问题,最后得到问题的解为:
⎰⎰
----∂∂
=M at
C
d d y x at t a t y x u ηξηξηξϕπ2
22)
()()()
,(21),,(+ +⎰⎰----∂∂M at
C
d d y x at t
a ηξηξηξφπ2
22)
()()()
,(21 称此式为二维波动方程柯西问题的泊松公式。
随了掌握这个公式,还要掌握这个公式的物理意义。