当前位置：文档之家 › 7-1 一维波动方程的达朗贝尔公式 chen

7-1 一维波动方程的达朗贝尔公式 chen

  • 格式：pdf
  • 大小：1012.51 KB
  • 文档页数：29

下载文档原格式

  / 29

合集下载

7.1达朗贝尔公式

7.1达朗贝尔公式

Wuhan University
u ( x, y ) = ?
答： x
五、小结
1、
§7.1
达朗贝尔公式
⎧utt = a 2uxx , − ∞ < x < ∞ (1) ⎪ ⎨u |t =0 = ϕ ( x) , − ∞ < x < ∞ (2) ⎪u | = ψ ( x), − ∞ < x < ∞ (3) ⎩ t t =0
u xx 1 1 ′′( x + at ) + ϕ ′′( x − at )] + = [ϕ [ψ ′( x + at ) − ψ ′( x − at )] 2 2a
Wuhan Uni7.1
达朗贝尔公式
1、适定性： （2）任意性已由初始条件唯一确定。 （3）稳定性：设
1 u ( x , t ) = [ϕ ( x + at ) + ϕ ( x − at ) 2 1 x + at + (6) ∫x − at ψ (α ) d α 2a
的解为
方程（1）的通解为
u ( x , y ) = f 1 ( x + at ) + f 2 ( x − at )
Wuhan University
2能否用行波法求解??????302sin010321xxuxxuuuuyyyxyxx???????????0cos110012222yyyuxxxuyxyxyxu71达朗贝尔公式3yxyx?????????????yxyx3本节作业习题71
Methods of Mathematical Physics 武汉大学 物理科学与技术学院
∂x ∂y ∂x ∂y
⎧uxx + 2uxy − 3u yy = 0 (1) ⎪ (1) ⎨u( x,0) = sin x (2) ⎪u ( x,0) = x (3) ⎩ y
第七章 波动方程初值问题

第七章 波动方程初值问题

x1 a(t0 t ) x0 at0
x1 x0 at
即, f1(x - at) 表示波速为 a 的右行波
同理可知, f2(x + at) 表示波速为 a 的左行波. 因此，行波解为左行波与右行波的叠加. 三. 半无界弦的自由振动
utt a 2 uxx 0 u x0 0 u t 0 ( x ), ut
二. 行波解的物理意义 行波法的通解为：
u( x, t ) f1 ( x at ) f 2 ( x at )
对 f1(x - at)，在 t0 时刻，x0 位置的波动位移为：
f1 ( x0 at0 )
若在t0+Δt 时刻, x1位置的波动位移也为 f1 ( x0 at0 ) 则：
t 0
a f1 ( x at ) x
f 2 ( x at ) t 0 a x
t 0
a f1 '( x ) a f 2 '( x ) y ( x )
对上式积分：
1 x x0 y ( )d [ f1 ( x ) f1 ( x0 )] [ f2 ( x ) f2 ( x0 )] (2) a
(1)
t 0
y ( x ) a f1 '( x ) a f 2 '( x )
1 x x0 y ( )d f1 ( x ) f 2 ( x ) c a
(2)
1 1 x c f1 ( x ) 2 [ ( x ) a x0 y ( )d ] 2 由 (1) (2) (x > 0) 解得： x f ( x ) 1 [ ( x ) 1 y ( )d ] c 2 2 a x0 2
(优选)一维波动方程的达朗贝尔公式

(优选)一维波动方程的达朗贝尔公式


u (x, y, z), t0
u t
t0
1(x,
y,
z).
这个定解问题仍可用行波法来解，不过由于坐标变量有三个，不能直 接利用§6.1节中所得到的通解公式。下面先考虑一个特例。
10
§ 9.2.1 三维波动方程的球对称解
球对称：u与 , 都无关。
在球坐标系中，三维波动方程为：
1 r2
r
r
1 a2
2 (ru) t 2
2 (ru) r 2
1 a2
2 (ru) t 2
这是关于ru的一维波动方程，其通解为：
ru f1(r at) f2 (r at)
或 u(r,t) f1(r at) f2 (r at) r
（9.1.7）
f1(x) f2 (x) (x) （9.1.8）
a f1(x) a f2(x) (x) （9.1.9）
5
f1(x) f2 (x) (x) （9.1.8）
a f1(x) a f2(x) (x) （9.1.9）
式（9.1.9）两端对 x 积分一次，得：
f1(x)
f2 ( x)
一维波动方程的达朗贝尔公式
求解定解问题
分离变量法——求解有限区域内定解问题：解的区 域比较规则（其边界在某种坐标系中的方程能用若 干个只含有一个坐标变量的方程表示）
行波法——求解无界区域内波动方程的定解问题 积分变换法——不受方程类型的限制，主要用于无
界区域，但对有界区域也能应用
2
§9.1 一维波动方程的D’Alember(达朗 贝尔)公式
到的波形为：(x at) (c at at) (c)
由于t为任意时刻，这说明观察者在运动过程中随时可看到相同的波 形，说明波形和观察者一样，以速度a沿x轴的正向传播。
一维波动方程的达郎贝尔公式

一维波动方程的达郎贝尔公式

一维波动方程的达郎贝尔公式1达郎贝尔公式在常微分方程的定解问题中，通常是先求方程的通解，然后利用定解条件确定通解所含的任意常数，从而得到定解问题的解。

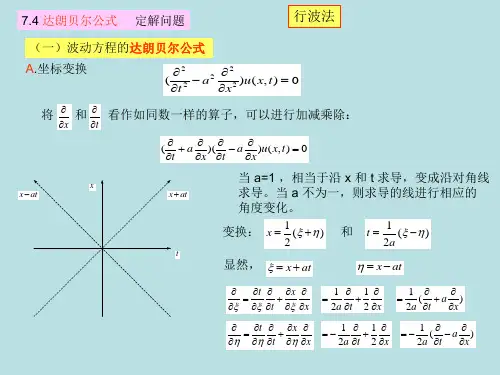
考虑无限长弦的自由振动问题⎪⎪⎩⎪⎪⎨⎧=∂∂=>+∞<<∞-∂∂=∂∂==)(|),(|0, ,0022222x tu x u t x xu a t u t t φϕ ① 作自变量的代换⎩⎨⎧-=+=atx atx ηξ 利用复合函数的微分法有：ηξ∂∂-∂∂=∂∂uau a t u )2(22222222ηηξξ∂∂+∂∂∂-∂∂=∂∂u u u a t u 同理有：22222222ηηξξ∂∂+∂∂∂+∂∂=∂∂uu u x u 将①化为：02=∂∂∂ηξu并将它两端对η进行积分得：)(0ξξf u=∂∂ 其中)(0ξf 是ξ的任意函数，再将此式对ξ积分)()()()(),(2120ηξηξξf f f d f t x u +=+=⎰=)()(21at x f at x f -++ ②其中21f f 、是任意两次连线可微函数，式②即为方程①的含有两个任意函数的通解。

由初始条件可得：)()()(21x x f x f ϕ=+)()()(2''1x x f x af φ=+通过积分可得：⎰+-+-++=atx at x d aat x at x t x u ξξϕφϕ)(21)]()([21),(称此式为一维波动方程的达郎贝尔公式。

2解的物理意义由于波动方程的通解是两部分)(1at x f +与)(2at x f -。

)(22at x f u -=表示了以速度a 向x 轴正方向传播的行波，称为右行波。

同理，)(11at x f u +=表示了以速度a 向x 轴负方向传播的行波，称为左行波。

由达郎贝尔公式，解在点),(t x 的值由初始条件在区间],[at x at x +-内的值决定，称区间],[at x at x +-为点),(t x 的依赖区域，在t x-平面上，它可看作是过点),(t x ，斜率分别a1± 为的两条直线在x 轴上截得的区间。

数学物理方法课件第七章-----行波法

数学物理方法课件第七章-----行波法


变量代换
x at
x at
2 u( , ) 0
a a u ( x, t ) 0 x t x t
u f1 ( ) f 2 ( )
行波法解题要领
• 行波法的提法来自于研究行进波。其解题要领为： • （1）引入特征变换，把方程化为变量可积的形式，从 而得到方程的通解； • （2）使用定解条件确定通解中的任意函数（对于常微 分方程为常数），从而得到其特解。 • 注意：由于偏微分方程求解较难，大部分偏微分方程 的通解均不易获得，使用定解条件确定其任意函数或 常数也绝非易事，故行波法也有其较大的局限性。但 是对于研究波动问题，行波法自有其独特的优点(实际 上我们主要只使用它研究波动问题)。因此行波法是求 解数学物理方程的基本的和主要的方法之一。
utt a u xx , ( Ⅰ )u |t 0 ( x) u | ( x) t t 0
2
- x
① ② ③
其中 ( x)和 ( x)为已知函数。
§7.1 行波法—一维波动方程的达朗贝尔解
解： 1 ）做特征变换，求定解问题Ⅰ中方程①的通 () 一、达朗贝尔公式 dx 2 ①的特征方程为： ( ) a2 0 算符分解 dt ①式 dx dx a a u 0 x0 x 即( a )(t a) t dt dt 从而得到两簇特征线 (积分后得到 )如下： x a( ) t 坐标变换： x at c1 , x at c2 做特征变换 x at x at ④
§7.1 行波法—一维波动方程的达朗贝尔解
一、达朗贝尔公式 利用复合函数求导法则，有 u u u u u x x x
一维波动方程的达朗贝尔公式

一维波动方程的达朗贝尔公式


2
2a xat
cos(at) cos x t e .
8
第8页/共44页
*§9.2 三维波动方程的Poisson公式
• 三维无限空间中的波动问题，即求解下列定解问题：
2u t 2
a
2
(
2u x2
2u y 2
2u z2 )
x, y, z ,t 0,
u (x, y, z), t0
u t
t0
6
第6页/共44页
所以 (x at)代表以速度a沿x轴的正向传播的波，称为正行波。而
第一项
(则x 代 表at以) 速度a沿x轴的负向传播的波，称为反行波。
正行波和反行波的叠加（相加）就给出弦的位移。
再讨论只有初速度的情况。此时式（9.1.11）给出：
u(x,t) 1
xat
( )d
2a xat
3
第3页/共44页
u(x,t) f ( )d f2() f1(x at) f2(x at) （9.1.6）
式（9.1.6）就是方程（9.1.1）的通解。
在具体问题中，我们并不满足于求通解，还要确定函数 与 f1的具f体2 形式。
为此，必须考虑定解条件。
下面我们来讨论无限长弦的自由横振动。设弦的初始状态为已知。
令 r 0利用L’Hospital（洛必塔）法则得到：
__
u (0,t)
___
0 (at)
___
at 0(at)
t
___
1 (at)
1 a
t
(at
)
___
0 (
at
)
t
___
1 (at)
1 0 (x sin cos, y sin sin, z cos ,t) (at)2 sin dd
一维波动方程的达朗贝尔公式

一维波动方程的达朗贝尔公式

t sin x cos at (3 x 2 a 2t 2 ) 3
x at
x at
2d
例2
utt a 2uxx 0, x x2 x2 u |t 0 e , ut |t 0 2axe
解：将初始条件代入达朗贝尔公式
x at
(x)
x1
x2
1 ( )d 2a
x at

( )d
( x at ) ( x at )
x
0
x1
x2
1 u ( x, t ) at ( )d 2a x 1 2a
x at
x at
1 ( )d 2a
e
( x at )2
1 ] （e 2
2
）
x at x at
( x at ) 2
例3
utt a 2uxx 0, x u |t 0 ( x), ut |t 0 ( x)
x x1 , x2 x1 x x2 , x2 x1 x1 x2 x1 x 2 x1 x2 x x2 2 x x1 , or , x x2
对第二式作定积分得：
1 x f1 ( x) f 2 ( x) ( )d f1 ( x0 ) f 2 ( x0 ) a x0
由此解得：
x 1 1 1 f1 ( x) 2 ( x) 2 a ( )d f1 ( x0 ) f 2 ( x0 ) x0 2 x f ( x) 1 ( x) 1 ( )d 1 f ( x ) f ( x ) 1 0 2 0 2 2 a x 2 0 2
波动方程的达朗贝尔解

波动方程的达朗贝尔解


简单方式
1 x 2 x at x at t 1 2a
2.波动方程的通解
2 u0
对 积分
u C1 f
对 积分
u f1 C2 f1 f 2
2）除了少数简单的例子，多数偏微分方程很 难求出通解。
3）即使能求出通解，对于具体的问题，要确定 其中的待定函数往往也并不容易。以达朗贝尔公 式为例，处理边界条件时就不是很方便。一些简 单情况下还可采用延拓的方法进行处理，对一般 的情况处理起来较繁琐。
4.半无界弦问题
utt a 2uxx u |t 0 u ( x, 0) x , ut |t 0 ut ( x, 0) x u 0, t 0
a b
1 f1 x f 2 x x dx f1 x0 f 2 x0 a x0
x
1 1 1 f1 x x d f1 x0 f 2 x0 2 2a x0 2
x
1 1 1 f2 x x d 2 f1 x0 f 2 x0 2 2a x0
1 1 u x, t x at x at 2a 2
1 1 x at x at 2a 2
sin( x at ) sin( x at ) 1 x at xat e d 2 2a sin( x at ) sin( x at ) 1 x at [e e x at ] 2 2a
通解法的缺点 1）以上解法类似于通常常微分方程的求解方法。 但是，对于通常的定解问题我们往往并不采用 求通解的方法来处理。
波动方程的达朗贝尔公式

波动方程的达朗贝尔公式

域是以x0为顶点的角状区域.
在上面的讨论中,我们看到了( x,t )平面上的直线 x ± at = c
(常数)对波动方程的研究起着重要的作用,它们称为波动 方程的特征线.
最后我们指出,在求解二阶方程线性常微分方程时,通 解中包含两个任意常数,因此,只须两个定解条件,就能完全 从中确定一个特解.
而今对于线性偏微分方程,比如对弦振动方程,在求得 达氏解,只用了两个定解条件,即两个初始条件,而在求的付 氏解时则又添了两个边界条件,一共用了四个边界条件.
那末,对于一个偏微分方程究竟要多少个定解条件,就 恰好(不多不少)能够从中确定一个特解呢?这一个问题没有 固定的答案.
这个事实,说明偏微分方程的定解问题比常微分方程要 复杂的多.
2.三维波动方程Cauchy问题的 Poisson公式
现在考察三维波动方程的初值问题
( ) ⎧⎪⎪⎨uut(t
= x,
a2Δu = a2
=
x+at)
+ϕ(
x-at)
2
给出.
为了简单起见,假设
⎧0
⎪
ϕ
(
x)
=
⎪⎪2 ⎨ ⎪⎪2
+ −
2x
α
2x
α
⎪⎩0
( x < −α ) (−α ≤ x ≤ 0)
(0 ≤ x ≤α) (x >α)
也就是说,初始位移是区间 [−α,α ] 上的一个等腰三角形.
图1给出了这个弦每经过时间
α
后的相对位移.
4a
0
y
x
u(M,t)
=
u ( x,
y, z,t)
=
∂ ∂t
⎡t
⎢⎣ 4π a2t2
A7.行波法求解一维波动方程的初值问题—半无界问题

A7.行波法求解一维波动方程的初值问题—半无界问题

行波法求解一维波动方程的初值问题—半无界问题行波法求解一维波动方程的两个基本公式：1.达朗贝尔（d'Alembert ）公式：⎰+-+-++=at x at x d aat x at x t x u ξξψφφ)(21))()((21),(； 2.Kirchhoff 公式：⎰⎰⎰----+-++-++=t t a x t a x at x at x d d f a d a at x at x t x u 0)()(),(21)(21))()((21),(τττξτξξξψφφ半无界弦的振动问题对于半无界域上波动方程初值问题的讨论，需要根据端点所处的物理状态不同分别加以讨论。

1. 端点固定（1）齐次端点条件 考虑定解问题.0,0,0,00),0(),()0,(),()0,(),,(2≥+∞<≤>+∞<<⎪⎩⎪⎨⎧===+=t x t x t u x x u x x u t x f u a u t xx tt ψφ求解上述问题的基本思路是以某种方式延拓函数,,,ψφf 使其在0<<∞-x 也有定义，这样把半无界区域+∞<≤x 0上的问题转变为+∞<<∞-x 上的初值问题。

然后利用达朗贝尔公式，求出在+∞<<∞-x 上的解),(t x u 。

同时使此解),(t x u 满足0),0(=t u 。

这样当x 限制在+∞<≤x 0上就是我们所要求的半无界区域+∞<≤x 0上的解。

由微积分知识可知，如果一个连续可微函数)(x g 在),(+∞-∞上是奇函数，则必有0)0(=g 。

因此，要使解),(t x u u =满足0),0(=t u ，只要),(t x u 是x 的奇函数便可。

因此对函数ψφ和,f 关于x 作奇延拓。

我们定义)()(),,(x x t x F ψΦ和如下：⎩⎨⎧≥<--≥≥⎩⎨⎧<≥--=ψ<≥⎩⎨⎧--=Φ.0,0),,(,0,0),,(),(.0,0),(),()(.0,0),(),()(t x t x f t x t x f t x F x x x x x x x x x x ψψφφ 显然函数在和)()(),,(x x t x F ψΦ+∞<<∞-x 上是奇函数。

达朗贝尔公式

达朗贝尔公式


t =0
= ψ ( x)
=0
达朗贝尔公式是无限长弦的公式。自变量限制为 x ≥ 0 。
1 1 u ( x, t ) = [ϕ ( x + at ) + ϕ ( x − at )] + ∫ ψ (ξ )dξ 2 2a x −at
x + at
t > x/a
u (0, t ) = 0
时，上式中后两项无意义。必须将 u(x,t) 延拓到这个范围。 ，作奇延拓： ϕ ( x) → Φ ( x)
x − at
x
x + at
当 a=1 ，相当于沿 x 和 t 求导，变成沿对角线 求导。当 a 不为一，则求导的线进行相应的 角度变化。 变换： x = (ξ + η )
1 2
和
t=
1 (ξ − η ) 2a
t
显然， ξ = x + at
∂ ∂t ∂ ∂x ∂ = + ∂ξ ∂ξ ∂t ∂ξ ∂x ∂ ∂t ∂ ∂x ∂ = + ∂η ∂η ∂t ∂η ∂x
= f1 ( x + at ) + f 2 ( x − at )
X = x − at T = t
新坐标的时间与旧坐标同，新坐标的原点 X=0 在旧坐标中有坐标 x = at ，即在 旧坐标中以速度 d 运动，而函数 f2(x-at) 保持形状不变，以速度 d 运动沿 x 轴 正方向运动。 f1 (x+at) 保持形状不变，以速度 d 运动沿 x 轴反方向运动。
7.4 达朗贝尔公式
定解问题
行波法
（一）波动方程的达朗贝尔公式 达朗贝尔公式 A.坐标变换
2 ∂2 2 ∂ ( 2 −a )u ( x , t ) = 0 ∂t ∂x 2

波动方程的达朗贝尔公式

(半径为at的球面元素) (半径为1的球面元素)
ϕ
0 x y
2π π ∂ ⎡ t ⎤ u ( M , t ) = u ( x, y , z , t ) = ⎢ ϕ (α , β , γ ) ds ⎥ 2 2 ∫0 ∫0 ∂t ⎣ 4π a t ⎦ 2π π 1 + ψ (α , β , γ )ds 2 2 ∫0 ∫0 4π a t 1 ⎡∂ ϕ (ξ ,η , ζ ) ψ (ξ ,η , ζ ) ⎤ ds + ∫∫ M ds ⎥ = M ⎢ ∂t ∫∫Sat (8) Sat 4π a ⎣ at at ⎦
代入(3)式,得 达朗贝尔公式
u ( x, t ) =
ϕ ( x + at ) + ϕ ( x − at )
2
1 x + at + ∫x−at ψ ( s )ds 2a
(7)
达朗贝尔公式的物理意义
通解
u ( x, t ) = F ( x − at ) + G ( x + at )
表示弦上的任意扰动总是以行波的形式向相反的 两个方向传播出去,故达朗贝尔解法又称为行波解法. a为波的传播速度.从分析a的量纲也可以知道a代表速度,因为
对式(5)从任意一点 x0 到
(4) (5)
x 积分,得
(6)
1 x F ( x ) − G ( x ) = c − ∫ ψ ( s )ds a x0
连立解(4),(6)得
1 1 x c F ( x) = ϕ ( x) − ∫x0 ψ ( s )ds + 2 2 2a 1 1 x c G ( x) = ϕ ( x) + ∫x0 ψ ( s )ds − 2 2 2a
即
u ( x, t ) = F ( x − at ) + G ( x + at )

波动方程的达朗贝尔公式

波动方程的达朗贝尔公式达朗贝尔公式是描述波动方程解的一种常见方法，它是由法国天文学家和数学家达朗贝尔于1787年提出的。

在描述一维波动问题时，达朗贝尔公式可以非常有效地解决问题。

首先，我们来看一维波动方程的基本形式：∂²u/∂t²=v²∂²u/∂x²其中u(x,t)表示波的位移，v表示波速，x表示空间坐标，t表示时间。

利用达朗贝尔公式，我们可以将一维波动方程的解表示为：u(x,t) = f(x+vt) + g(x-vt)其中f(x)和g(x)是任意两个可微函数。

达朗贝尔公式的推导可以通过变量分离法得到。

首先，我们将u(x,t)表示为两个变量的函数u(x,t)=F(x)G(t)，然后将其代入波动方程：F''(x)G(t)=v²F(x)G''(t)两边除以v²FG，得到：F''(x)/F(x)=G''(t)/G(t)等式左边只依赖于x，右边只依赖于t，所以两边都等于一个常数k²：F''(x)/F(x)=G''(t)/G(t)=k²然后我们分别解这两个常微分方程。

对于F''(x)/F(x)=k²，我们可以得到解：F(x) = A e^(kx) + B e^(-kx)对于G''(t)/G(t)=k²，我们可以得到解：G(t) = C e^(ikt) + D e^(-ikt)其中A、B、C和D为任意常数，i为虚数单位。

因此u(x,t) = F(x)G(t) = [A e^(kx) + B e^(-kx)][C e^(ikt) + De^(-ikt)]我们可以通过组合常数A、B、C和D得到f(x)和g(x)。

根据指数函数的性质，我们可以将解写成达朗贝尔公式的形式：u(x,t) = f(x+vt) + g(x-vt)其中f(x+vt) = (A e^(kx) + B e^(-kx)) (C e^(ikt) + D e^(-ikt))g(x-vt) = (A e^(kx) + B e^(-kx)) (C e^(ikt) + D e^(-ikt))达朗贝尔公式的形式表明，波动方程的解可以表示为由两个运动方向相反的平面波的叠加形式。

7-1 一维波动方程的达朗贝尔公式 chen


t
( x, t )
依赖区间
O x − at
x + at x
退出
数学物理方程与特殊函数 主页 上一页 下一页
t
x=
t
t
x1
x=
O
x1
x2
x
O
x1
x2
决定区间
影响区间
在区间[ x1 , x2 ]上给定初始条件,就可以在其决定 区间域中决定初值问题的解.
数学物理方程与特殊函数 主页 上一页 下一页 退出
退出
因为在特征线 x − at = C 2 上,右行波 u2 = f 2 ( x − at ) 的振幅取常数值 f 2 (C 2 ) ,在特征线 x + at = C1 上,左行波 u 1 = f1 ( x + at )的振幅取常数值 f1 (C1 ) ,且这两个数值随 特征线的移动(即常数 C i ( i = 1, 2) 的改变)而改变,所以波 动实际上是沿特征线传播的.
⎧ uxx + 2uxy − 3u yy = 0 ⎪ ⎨ 2 ⎪u | y=0 = 3 x , uy | y=0 = 0 ⎩
y > 0, −∞ < x < +∞
−∞ < x < +∞
先确定所给方程的特征线.为此写出它的特征方程: 它的两族积分线为:
(dy )2 − 2dxdy − 3(dx )2 = 0
主页上一页下一页退出数学物理方程与特殊函数由此可以看出在xt平面上斜率为的两族直线常数对一维波动方程的研究起着重要的作用我们称其为一维波动方程ttxxttxx主页上一页下一页退出数学物理方程与特殊函数因为在特征线上右行波的振幅取常数值在特征线上左行波的振幅取常数值且这两个数值随特征线的移动即常数的改变而改变所以波动实际上是沿特征线传播的

第三章 一维波动方程的达朗贝尔公式-1

深圳大学电子科学与技术学院
第三章：行波法与积分变换法
§3.1 一维波动方程的达朗贝尔公式
深圳大学电子科学与技术学院
深圳大学电子科学与技术学院
本章内容提要:
• 一维波动方程的达朗贝尔公式
• 三维波动方程的定解问题
• 拉普拉斯变换法
• 傅立叶变换法
• 积分变换法举例 参考了顾樵教授和孙秀泉教授的课件
深圳大学电子科学与技术学院
结果：
1 1 x at (1747) u ( x, t ) ( x at) ( x at) ( X ) d X 2 2a x at
2 2u u 2 a 2 t x 2
( x )， u t 0
u ( x), ( x) t t 0
深圳大学电子科学与技术学院
波动方程的特解
无界弦的自由振动: 任意初始位移,任意初始速度。 无界弦自由振动的初值问题为：
2 2u 2 u a t 2 x 2
( x ) u t ( x)
t 0
（1）
u t 0 ( x),
( x )
（2）
将(1)化成以 , 为变量:
u u u u u x x x 2u u u u u 2 x x x u u u u 2u 2u 2u 2 2 2
（3）
(1)的通解为： u( x, t ) f1 ( x at) f 2 ( x at)
由(2)得到：
u
t 0
f1 ( x) f 2 ( x) ( x )

《数理方程》波动方程的达朗贝尔公式


反过来,我们考虑这样的问题:如果在初始时刻t=0,扰动仅在 一有限区间 x1, x2 上存在,那末,经过时间t后,它所影响到的范 围是什么? 在 x, t 平面上,过
x1,0 和 x2 ,0 两点,分别作直线,
(i) (ii)
x x1 at
x x2 at
(半径为at的球面元素) (半径为1的球面元素)

x 0 y
2 t u M , t u x, y , z , t , , ds 2 2 0 0 t 4 a t 2 1 , , ds 2 2 0 0 4 a t 1 ( , , ) ( , , ) ds M ds M (8) S S at 4 a t at at at
utt a uxx .
2
(iii)
如果要求u1还满足初始速度,则只须把被积函
数 x 换为 x .
问题的解了.
如果还要求u2满足初始位移,则
只须将 x 换为 x .两者都换了之后,u1+u2就成了定解
现在仿照公式(7)’构造三维波动方程初值问题的达氏解. 为此,先作一些对应的讨论:(列在下一页)
依赖区间
决定区域和影响区域
下面我们提出这样一个问题:上述初值问题的解在一 点 x0 , t0 的值与初值函数在x轴上哪些点的值有关呢?
为此,在 x, t 平面上,过点 x0 , t0 作两条直线
x at x0 at0 x1 (i) x at x0 at0 x2 (ii)
对式(5)从任意一点 x0 到
(4) (5)
x 积分,得
(6)

07第七章 行波法


∫ ∫ 特解 uspecial = − dξ dη f ( a ξ + aη, ξ − η)
• 二维泊松方程 ux x + uy y = f ( x, y) 的特解？ a → i, t → y
5
3. 一维波动方程的达朗贝尔公式
∫ u( x, t) = ϕ( x − at) + ϕ( x + at) + 1 x+atψ(α)dα
− f1′(3x) + f2′(x) = x
−
1 3
f1(3x) +
f2( x)
=
1 2
x2
+c
f1(3x)
=
3 4
(sin
x
−
c
−
1 2
x2
),
f2
(
x)
=
1 4
(sin
x
+
3
c
+
3 2
x2
)
u=
f1[3(x −
y )]+ 3
f2(x +
y)
= 1 sin(x + y) + 3 sin(x − y ) + x y + y2
x+a t
2dα
2
2a x −a t
= cosx cos(a t) + 2t
(2) 因式分解 ux x + 2ux y −3u y y = (∂ x + 3∂ y )(∂ x − ∂ y )u = uξη
∂ξ ∂
= ∂x η=∂
+ 3∂y x −∂y
dx = dξ + dη dy = 3dξ − dη
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

ξ = x + at , η = x − at ,
退出
数学物理方程与特殊函数 主页 上一页 下一页
⎧ξ = x + at 在变换 ⎨ ⎩η = x − at
下， 利用复合函数微分法则得:
∂u ∂ u ∂ξ ∂ u ∂ η ∂ u ∂ u = + = + ∂x ∂ξ ∂x ∂ η ∂ x ∂ ξ ∂ η
∂ u ∂ u ∂ u ∂ u = 2 +2 + 2 2 ∂x ∂ξ ∂ξ∂η ∂η
2 2 2 2
同理有:
⎡ ∂ 2u ∂ 2u ∂ 2u ∂ 2u ⎤ = a2 ⎢ 2 − 2 + 2⎥ 2 ∂t ∂ξ∂η ∂η ⎦ ⎣ ∂ξ
退出
数学物理方程与特殊函数 主页 上一页 下一页
用行波法求解这一问题,首先要求出 utt = a uxx 的 通解.可作如下代换: ⎧ξ = x + at ⎨ ⎩η = x − at
数学物理方程与特殊函数 主页 上一页 下一页 退出
一维齐次波动方程
utt = a uxx
2
的通解为:
u( x , t ) = f1 ( x + at ) + f 2 ( x − at )
其中 f1 , f 2 都是任意二次连续可微函数.
数学物理方程与特殊函数 主页 上一页 下一页
退出
利用初始条件来确定通解中的任意函数 f1 , f 2 .将 通解代入定解条件中,得:
退出
因为在特征线 x − at = C 2 上,右行波 u2 = f 2 ( x − at ) 的振幅取常数值 f 2 (C 2 ) ,在特征线 x + at = C1 上,左行波 u 1 = f1 ( x + at )的振幅取常数值 f1 (C1 ) ,且这两个数值随 特征线的移动(即常数 C i ( i = 1, 2) 的改变)而改变,所以波 动实际上是沿特征线传播的.
u( x , y ) = f1 (3 x − y ) + f 2 ( x + y )
数学物理方程与特殊函数 主页 上一页 下一页
退出
例题
代入 u | y = 0 = 3 x , u y | y = 0 = 0 得:
2
⎧ f1 (3 x ) + f 2 ( x ) = 3 x 2 ⎪ ⎨ ⎪ − f1′(3 x ) + f 2′( x ) = 0 ⎩ 1 − f1 (3 x ) + f 2 ( x ) = C 3 f1 (3 x ) = (4 9) x 2 − C ′
数学物理方程与特殊函数 主页 上一页 下一页 退出
对于常微分方程
⎧ y′′( t ) = 0 ⎪ ⎨ y′(0) = 1 3 ⎪ y(0) = 0 ⎩
B=0
先求通解: y( t ) = At + B
⎧ A·0 + B = 0 再用初始条件求特解: ⎨ ⎩A = 1 3
y( t ) = (1 3)t
2
利用复合函数微分法则得: ∂u ∂ u ∂ξ ∂ u ∂ η ∂ u ∂ u = + = + ∂x ∂ξ ∂x ∂ η ∂ x ∂ ξ ∂ η
∂ u ∂ u ∂ u ∂ u = 2 +2 + 2 2 ∂x ∂ξ ∂ξ∂η ∂η
2 2 2 2
数学物理方程与特殊函数 主页 上一页 下一页
退出
代入 utt = a 2 uxx 得:
u = f1 ( x + at ) + f 2 ( x − at )
再Байду номын сангаас特解,形如:
1 u= [ 2 1 ] + 2a ∫
退出
数学物理方程与特殊函数 主页 上一页 下一页
2.特点: (1)求解出发点是基于波动现象的特点为背景的变量 变换; (2)引入了坐标变换简化方程; (3)优点: 求解方式易于理解,求解波动方程十分方便; (4)缺点: 通解不易求,使之有局限性,一般只用它求解 波动问题.
⎧ξ = x + at 变换 ⎨ 常称为特征变换,行波法称为特征线法. ⎩η = x − at
数学物理方程与特殊函数 主页 上一页 下一页 退出
1.解题步骤:
⎧ utt = a 2 uxx ⎪ ⎨ u |t = 0 = ϕ ( x ) ⎪u | = ψ ( x) ⎩ t t =0
utt = a 2 uxx 求出通解: 先用
数学物理方程与特殊函数 主页 上一页 下一页 退出
所以在有限的时间内,当初始条件有微小改变 时,其解也只有微小改变,即达朗贝尔解是稳定的. 综上所述,达朗贝尔解是适定的.
数学物理方程与特殊函数 主页 上一页 下一页
退出
u1 = f1 ( x − at ) 表示一个以速度a 沿x 轴正方向传 播的行波,称为右行波. u2 = f 2 ( x + at ) 表示一个以速度a 沿x 轴负方向传 播的行波,称为左行波. 右行波和左行波的叠加(相加)就给出弦的位移. 即达朗贝尔解表示右行波和左行波的叠加.
u( x , t ) = f1 ( x + at ) + f 2 ( x − at )
⎧ u( x , 0) = ϕ ( x ) ⎨ ⎩ ut ( x , 0) = ψ ( x )
⎧ f1 ( x ) + f 2 ( x ) = ϕ ( x ) ⎨ ⎩ af1′( x ) − af 2′( x ) = ψ ( x )
x=
x1
x
+a t
x= x1 t −a
+a
x1 t −a
由此可以看出,在 x-t
1 平面上斜率为 ± a
的两族直线
x ± at = 常数,对一维波动方程 utt = a 2 uxx 的研究起着
utt = a 2 uxx 的 重要的作用,我们称其为一维波动方程
特征线.
数学物理方程与特殊函数 主页 上一页 下一页
数学物理方程与特殊函数 主页 上一页 下一页
退出
1 1 x C f1 ( x ) = ϕ ( x ) + ∫0 ψ (ξ )dξ + 2 2 2a 1 1 x C f2 ( x) = ϕ ( x) − ∫0 ψ (ξ )dξ − 2 2 2a 将上式代回到 u( x , t ) = f1 ( x + at ) + f 2 ( x − at )
数学物理方程与特殊函数 主页 上一页 下一页 退出
23
例题
求解弦振动方程的柯西问题 ⎧ ∂ 2u ∂ 2u ( t > 0, −∞ < x < ∞ ) − 2 =0 ⎪ 2 ∂t ∂x ⎨ ⎪ u( x , 0) = x , u ( x , 0) = sin x ( −∞ < x < ∞ ) t ⎩ 由达朗贝尔公式可得其解为：
1 1 x + at u( x , t ) = [ϕ ( x + at ) + ϕ ( x − at )] + ∫x −at ψ (ξ )dξ 2 2a
这就是达朗贝尔公式或称为达朗贝尔解.
中,即得方程定解问题的特解:
数学物理方程与特殊函数 主页 上一页 下一页
退出
易于验证,只要φ 有直到二阶的连续导数,ψ 有一阶 的连续导数,达朗贝尔解是满足定解问题的,即达朗贝尔 解是存在的. 又从求解的方法中看到,通解中的任意函数以由初 始条件完全确定,故达朗贝尔解是唯一的. 现在来证明达朗贝尔解的稳定性.设初始条件有两 组,且它们相差很小,即: ⎧ψ 1 ( x ) ⎧ϕ1 ( x ) u |t = 0 = ⎨ ; ut |t = 0 = ⎨ ϕ2 ( x) ⎩ψ 2 ( x ) ⎩
3x − y = C1 x + y = C2
数学物理方程与特殊函数 主页 上一页 下一页
退出
例题
作特征变换
⎧ξ = 3x − y ⎨ ⎩η = x + y
它的通解为:
∂ 2u 16 =0 ∂ξ∂η
u = f1 (ξ ) + f 2 (η )
其中 f1 , f 2 都是任意二次连续可微函数.原方程的通解 为:
⎡ ∂ 2u ∂ 2u ∂ 2u ∂ 2u ⎤ 2 =a ⎢ 2 −2 + 2⎥ 2 ∂t ∂ξ∂η ∂η ⎦ ⎣ ∂ξ
⎛ ∂ 2u ∂ 2u ∂ 2u ∂ 2u ⎞ = a2 2 = a2 ⎜ 2 + 2 + 2⎟ ∂x ∂ξ∂η ∂η ⎠ ⎝ ∂ξ
化简， 得:
∂ 2u =0 ∂ξ∂η
退出
数学物理方程与特殊函数 主页 上一页 下一页
t
( x, t )
依赖区间
O x − at
x + at x
退出
数学物理方程与特殊函数 主页 上一页 下一页
t
x=
t
t
x1
x=
O
x1
x2
x
O
x1
x2
决定区间
影响区间
在区间[ x1 , x2 ]上给定初始条件,就可以在其决定 区间域中决定初值问题的解.
数学物理方程与特殊函数 主页 上一页 下一页 退出
⎧ uxx + 2uxy − 3u yy = 0 ⎪ ⎨ 2 ⎪u | y=0 = 3 x , uy | y=0 = 0 ⎩
y > 0, −∞ < x < +∞
−∞ < x < +∞
先确定所给方程的特征线.为此写出它的特征方程: 它的两族积分线为:
(dy )2 − 2dxdy − 3(dx )2 = 0
数学物理方程与特殊函数 主页 上一页 下一页
退出
思考: 达朗贝尔公式表示，由任意初始扰动引起的 自由振动以行波的形式向正、反两个方向传播出 去，传播的速度正好等于泛定方程中的常数 a .