一维波动方程推导教学内容

一维波动方程的推导波动方程是研究波动现象的基本方程，可以用于描述电磁波、声波、水波等物理现象。

本文重点介绍一维波动方程的推导，该方程用于描述一条细长的弹性介质中的波动。

一、假设考虑一根无限长细弹性介质（如一根线），其质量和长度均匀分布在整个介质中。

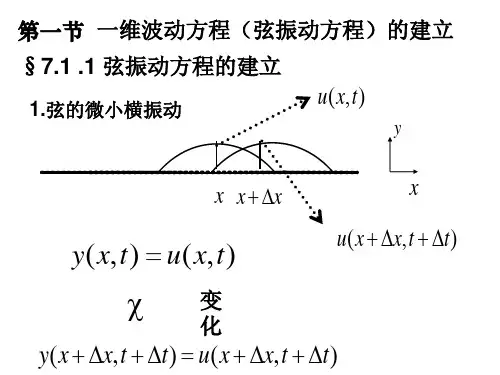
为简化情况，我们假设该介质在垂直于其初始方向的方向上运动（如在横向振动）。

为进一步简化情况，我们也假设振动幅度很小且初始速度为零。

这些假设可以使我们向更简单的物理模型过渡。

二、波动方程的推导根据牛顿第二定律可得，在 x 处截面内的物质元素受到 x+dx 处截面内的物质元素产生的力的作用。

因此，其受力可以表示为：F = ma = ρdx · A(x+dx) - ρdx · A(x) (1)其中，ρ表示介质的密度，A(x)表示在 x 处截面内的介质的横截面积，dx表示两截面之间的距离。

根据胡克定律可得，介质受到的合力可以表示为：F = -k[dA(x+dx) - dA(x)] (2)其中，k表示介质的弹性系数。

将公式（1）和公式（2）代入牛顿第二定律可得：ρA(x) ∂^2u/∂t^2 · dt = k[dA(x+dx) - dA(x)] (3)这里，u(x, t)表示在 x 处的位移，t表示时间。

我们可以化简后的上面公式为：∂^2u/∂t^2 = (k/ρA(x)) [A(x+dx) - A(x)]/dx (4)引入波速 c 来替换k/ρ，c 的定义为：c = sqrt(k/ρ) (5)则公式（4）可以简化为：∂^2u/∂t^2 = (c^2/dx^2) [A(x+dx) - A(x)] (6)通过对这一细弹性介质的初始状态和运动方式的假设，我们推导出一维波动方程。

这个方程描述了弹性介质中的波动，具有广泛的应用价值。

它可以应用于物理、地质学和工程学中等多领域。

一维波动方程的推导一维波动方程是描述一维介质中传播的波动现象的数学模型，它可以应用于声波、水波、电磁波等各种波动现象的研究。

其基本假设是介质中的波动是沿着介质传播的。

在推导一维波动方程时，我们需要先建立波动现象的数学模型。

假设介质中的波动是沿着x轴方向传播的，用u(x,t)表示波动处于x 点时的位移量。

我们需要考虑介质中的质点在时间t和t+Δt之间发生的位移量，即Δu(x,t)=u(x,t+Δt)-u(x,t)。

根据牛顿第二定律，质点在单位时间内所受到的合力等于质点的质量乘以加速度。

因此，介质中的质点在时间t和t+Δt之间的加速度可以表示为：a(x,t) = 1/ρ(x) * F(x,t)其中，ρ(x)是介质在x点处的密度，F(x,t)是介质在x点处的作用力。

根据胡克定律，介质中的质点在受到作用力时会发生弹性形变。

弹性形变的大小与作用力成正比，与介质的弹性系数成反比。

因此，介质在x点处的作用力可以表示为：F(x,t) = E(x) * u(x,t)/x其中，E(x)是介质在x点处的弹性系数，u(x,t)/x是介质在x点处的曲率。

将上述两个式子代入到a(x,t)的表达式中，得到：a(x,t) = 1/ρ(x) * E(x) * u(x,t)/x在介质中传播的波动是一种能量传输的过程。

波动在传播过程中，会带动介质中的质点振动，将能量从一个点传递到另一个点。

因此，介质中传播的波动在时间和空间上都是具有连续性的。

由此，我们可以得到波动方程的基本表达式：u(x,t)/t = c * u(x,t)/x其中，c=E/ρ，表示波动在介质中传播的速度的平方。

这就是一维波动方程的基本表达式。

在具体的应用中，我们需要根据不同的介质和波动特性，选择不同的初始条件和边界条件，来求解波动方程。

课程设计波动方程一、教学目标本节课的学习目标为：知识目标：学生能够理解波动方程的基本概念，掌握一维波动方程的求解方法。

技能目标：学生能够运用波动方程解决实际问题，如声波传播、振动等问题。

情感态度价值观目标：通过学习波动方程，培养学生对物理学科的兴趣和好奇心，提高学生分析问题和解决问题的能力。

二、教学内容本节课的教学内容主要为：1.波动方程的基本概念，包括波动、波速、波长等。

2.一维波动方程的求解方法，包括初始条件和边界条件的设定，以及求解过程的推导。

3.波动方程在实际问题中的应用，如声波传播、振动等问题的解决。

三、教学方法为了提高教学效果，本节课将采用以下教学方法：1.讲授法：用于讲解波动方程的基本概念和求解方法。

2.讨论法：引导学生分组讨论实际问题，培养学生的合作能力和解决问题的能力。

3.案例分析法：通过分析具体案例，使学生更好地理解波动方程的应用。

4.实验法：安排实验环节，让学生亲身体验波动现象，提高学生的实践能力。

四、教学资源为了支持教学内容和教学方法的实施，本节课将准备以下教学资源：1.教材：提供波动方程的相关理论知识。

2.参考书：为学生提供更多的学习资料，丰富学生的知识体系。

3.多媒体资料：通过动画、视频等形式，形象地展示波动现象，提高学生的学习兴趣。

4.实验设备：为学生提供实验所需的器材，确保实验环节的顺利进行。

五、教学评估本节课的评估方式包括：1.平时表现：通过观察学生在课堂上的参与程度、提问回答等情况，评估学生的学习态度和理解程度。

2.作业：布置与本节课内容相关的作业，评估学生对波动方程知识的掌握情况。

3.考试：安排一次考试，全面测试学生对波动方程的理解和应用能力。

评估方式应客观、公正，能够全面反映学生的学习成果。

通过这些评估方式，教师可以了解学生的学习情况，及时给予反馈和指导。

六、教学安排本节课的教学安排如下：1.教学进度：按照教材的章节安排，逐步讲解波动方程的基本概念、求解方法和应用。

第二章 波行法本章将利用行波法和球平均法分别求解一维和二维、三波动方程Cauchy 问题的§1 一维波动方程的Cauchy 问题一、 D ’Alembert 公式考虑初始位移为)(x ϕ，初始速度为)(x ψ的无界弦的自由振动，该振动可以归结为如下初值问题：()()⎪⎪⎩⎪⎪⎨⎧+∞<<∞-=+∞<<∞-=>+∞<<-∞=-==x x u x x u t x u a u t t t xx tt )()()0,(0002ψϕ（2.1） 由第一章第三节弦振动方程可经自变量变换简化，作变换：⎩⎨⎧+=-=atx atx ηξ 由ηξηξηξu u u u u x x x +=+=ηηξηξξηηξξηξηξu u u u u u u u x x xx ++=+++=2)()()(ξηηξu u a au au u t -=+-=)(2ηηξηξξu u u a u tt +-=代入方程(2.1)得042=-ξηu a由 02>=ρTa ，有0=ξηu先对η积分,得()uf ξξ=其中()f ξ是任意的函数,再ξ对积分,得到212()()()()u f d F F F ξξηξη=+=+⎰其中12,F F 都是任意的函数.把,ξη换成x,t 的表示式,即得)()(),(21at x F at x F t x u ++-= (2.2) (2.2)给出的仅仅是泛定方程的解为了得到满足(2.1)的解,考虑初值条件)()()()0,(21x x F x F x u ϕ=+= (2.3) 和)()()()0,(21x dx x dF dxx dF a x u t ψ=⎥⎦⎤⎢⎣⎡+-= (2.4) 将(2.4)两端取从0x 到x 积分：[]⎰=++-xx d C x F x F a 0)()()(21ααψ (2.5) 其中)]()([,02010x F x F a C x -=任意. 联立(2.4)和(2.5)，解得：a Cd a x x F x x 2)(21)(21)(01+⎰-=ξξψϕ a Cd a x x F x x 2)(21)(21)(02-⎰+=ξξψϕ将以上两式代入(2.2)即得Cauchy 问题(2.1)的解 ⎰+++-=+-atx at x d aat x at x t x u ξξψϕϕ)(212)()(),(这叫做一维波动方程Cauchy 问题的D ．’．Alembert ．．．．．．．．公．式．.。

一维波动方程可用如下的方式推导：一列质量为m的小质点，相邻质点间用长度h的弹簧连接。

弹簧的劲度系数（又称“倔强系数”）为k：
其中u(x) 表示位于x的质点偏离平衡位置的距离。

施加在位于x+h处的质点m上的力为：
其中代表根据牛顿第二定律计算的质点惯性力，代表根据
胡克定律计算的弹簧作用力。

所以根据分析力学中的达朗贝尔原理，位于x+h处质点的运动方程为：
式中已注明u(x) 是时间t的显函数。

若N个质点间隔均匀地固定在长度L = N h的弹簧链上，总质量M = N m，链的总体劲度系数为K = k/N，我们可以将上面的方程写为：
取极限N, h就得到这个系统的波动方程：
在这个例子中，波速。