6第六章 梁的应力解析

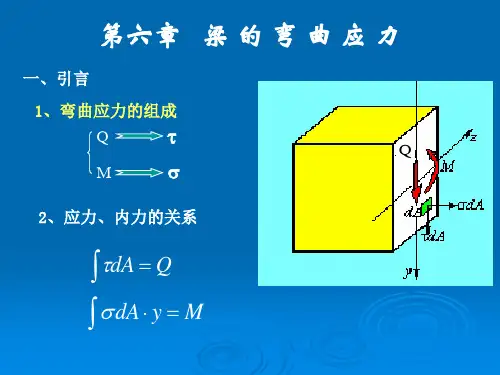
第六章 梁的应力§6-1 梁的正应力 回顾与比较： 内力 应力FN σ = ATTρ τ = IPM FSFAy§6-1 梁的正应力MdAσ dAFAyFSτ dAσ⇔Mτ ⇔ FS在横截面上，只有法向内力元素dFN=σdA才能合成M, 只有切向内力元素dFS=τdA才能合成剪力FS。

§6-1 梁的正应力 纯弯曲：Fs图 M图 梁段CD上，只有弯矩，没有剪力－－纯弯曲 梁段AC和BD上，既有弯矩，又有剪力－－横力弯曲§6-1 梁的正应力 思路： 实验观察得应变ε的变化规律(变形几何关系)⎯⎯⎯ → (物理关系)静力平衡条件(静力学关系)σ = Eε应力σ的变化规律⎯⎯⎯⎯⎯ → 横截面上任一点的正应力公式§6-1 梁的正应力 变形几何关系:用较易变形的材料制成的矩形截面等直梁作纯弯曲试验:Me Me§6-1 梁的正应力 实验观察： (1)变形前互相平行的纵向直线，变形后均变 为圆弧，且凸边伸长，凹边缩短； (2)变形前垂直于纵向线的横向线，变形后仍 为直线，且仍与纵向曲线正交。

Me Me§6-1 梁的正应力 实验分析: Me Me (1) 平面假设梁在纯弯曲时的平面假设： 梁的各个横截面在变形后仍保持为平面， 并仍垂直于变形后的轴线，只是横截面绕某一 轴旋转了一个角度。

§6-1 梁的正应力 (2) 单向受力假设 梁的各纵向层互不挤压或牵拉，各纵向 “纤维”均只受到拉伸或压缩的作用。

§6-1 梁的正应力 (3) 梁变形后，同一层纵向纤维的长度相同，即 同层各条纤维的伸长（或缩短）相同。

§6-1 梁的正应力 凹入一侧纤维缩短 中间一层纤维长度不变 中性层与横截面的交线 凸出一侧纤维伸长 ——中性层 ——中性轴重要结论：中性轴z轴必定通过截面的形心§6-1 梁的正应力 计算梁的弯曲正应力的一般公式：My σ= IzI Z = ∫ y dA2 A§6-1 梁的正应力 正应力分布： σ = I zMyzy yzzy yz§6-1 梁的正应力 最大正应力：My σ= IZσ maxMymax = IZ当中性轴是横截面的对称轴时： 令σ maxIZ WZ = ymaxσ maxM = WZσ maxWz——抗弯截面模量，是一个仅与 截面的形状和尺寸有关的几何量。

梁的应力计算公式全部解释应力是材料受力时产生的内部力，它是描述材料内部抵抗外部力的能力的物理量。

在工程领域中，计算材料的应力是非常重要的，可以帮助工程师设计和选择合适的材料，以确保结构的安全性和稳定性。

梁的应力计算公式是计算梁在受力时产生的应力的公式，它可以帮助工程师了解梁在不同条件下的应力情况，从而进行合理的设计和分析。

梁的应力计算公式是由弹性力学理论推导而来的，它可以根据梁的几何形状、受力情况和材料性质来计算梁的应力。

在工程实践中，梁的应力计算公式通常包括弯曲应力、剪切应力和轴向应力三种类型的应力。

下面将分别对这三种类型的应力计算公式进行详细解释。

1. 弯曲应力计算公式。

梁在受到外部力的作用时，会产生弯曲应力。

弯曲应力是由于梁在受力时产生的弯曲变形所引起的，它可以通过以下公式进行计算：σ = M c / I。

其中，σ表示梁的弯曲应力，单位为N/m^2；M表示梁的弯矩，单位为N·m；c表示梁截面内的距离，单位为m；I表示梁的惯性矩，单位为m^4。

弯曲应力计算公式可以帮助工程师了解梁在受力时产生的弯曲应力大小，从而进行合理的设计和分析。

在工程实践中，通常会根据梁的几何形状和受力情况选择合适的弯曲应力计算公式进行计算。

2. 剪切应力计算公式。

梁在受到外部力的作用时，会产生剪切应力。

剪切应力是由于梁在受力时产生的剪切变形所引起的，它可以通过以下公式进行计算：τ = V Q / (I b)。

其中，τ表示梁的剪切应力，单位为N/m^2；V表示梁的剪力，单位为N；Q 表示梁的截面偏心距，单位为m；I表示梁的惯性矩，单位为m^4；b表示梁的截面宽度，单位为m。

剪切应力计算公式可以帮助工程师了解梁在受力时产生的剪切应力大小，从而进行合理的设计和分析。

在工程实践中，通常会根据梁的几何形状和受力情况选择合适的剪切应力计算公式进行计算。

3. 轴向应力计算公式。

梁在受到外部力的作用时，会产生轴向应力。

轴向应力是由于梁在受力时产生的轴向变形所引起的，它可以通过以下公式进行计算：σ = N / A。

材料力学梁的应力知识点总结梁是一种常见的结构元件，在工程中广泛应用。

了解梁的应力知识点对于工程设计和分析非常重要，本文将对材料力学梁的应力知识点进行总结。

1. 弯曲应力在弯曲载荷下，梁会发生弯曲变形，产生弯曲应力。

弯曲应力分为正应力和剪应力两部分。

梁的顶端受拉产生正应力，底端受压产生正应力。

横截面上由于剪力的存在，产生剪应力。

弯曲应力与梁的几何形状、材料性质和载荷有关。

2. 矩形截面的弯曲应力分布对于矩形截面的梁，弯曲应力的分布是不均匀的。

顶部和底部的纤维受到最大应力，处于拉伸或压缩状态。

靠近中性轴的纤维受到较小的应力。

弯曲应力的分布可用弯矩与惯性矩的比值来表示。

3. 剪应力和剪力流在梁的截面上，由于剪力的存在，产生剪应力。

剪应力的分布是沿纵横两个方向呈对称分布的。

剪应力在截面上的变化呈线性分布，最大值出现在截面的边缘。

剪力流是指单位深度上的剪力大小，剪应力和剪力流之间存在直接的线性关系。

4. 应力分量的变换在梁的应力分析中，常常需要对应力分量进行变换。

常用的应力分量变换公式有平面应力变换公式和平面应变变换公式。

5. 横截面形状的影响梁的横截面形状对其应力分布和强度有显著影响。

常见的梁截面形状有矩形、圆形和I型等。

圆形截面具有均匀的应力分布特点，适用于承受压力的情况。

I型截面具有较高的抗弯强度，适用于悬挑梁和跨大距离的情况。

6. 梁的断裂当梁受力达到其强度极限时，可能会发生断裂。

断裂形式可以是横断面的剪断、疲劳断裂或脆性断裂等。

设计中需要考虑梁的强度和刚度，以避免出现断裂。

总结：材料力学梁的应力知识点对于工程领域非常重要。

弯曲应力、剪应力和剪力流是梁应力分析的关键内容；矩形截面的弯曲应力分布是不均匀的，可以用弯矩与惯性矩的比值表示；横截面形状对梁的应力分布和强度有重要影响。

通过深入理解和应用这些知识点，可以对梁的行为和性能进行合理评估和设计。

材料力学梁的应力解读
梁是结构分析中最基本的问题之一，也是材料力学中一个重要的概念。

梁的应力解读，就是对梁结构中的应力的分析。

一般来说，在材料力学中，梁的应力解读可以从下面几个方面来进行：
（1）弯曲应力：弯曲应力是指当梁在受到外力的作用下发生偏移或
沿着其中一轴线变形时，梁中钢材筋的纵向应力称为弯曲应力。

根据梁的
预定约束方式，可以分为受自重弯曲的应力和受外力弯曲的应力。

受自重
弯曲的应力大小由梁的自重和梁的几何形态所决定，一般情况下，斜梁的
自重弯曲应力会比悬臂梁的自重弯曲应力大。

受外力弯曲的应力大小取决
于受力梁的拉张性和刚度，以及施加外力的位置，大小和作用方向等因素，其中最重要的是材料的弹性模量。

（2）剪切应力：梁结构的剪切应力，是指梁受到外力作用时，对面
两侧的钢材筋之间的剪切应力。

由于受力面两端受非对称分布的外力作用，使得受力面的梁结构受到剪切应力的作用，一般情况下，受力面梁结构分
布的剪切应力会在受力面的两端有最大值，随着回头距离变小而逐渐减小。

（3）压应力：梁受外力所产生的压应力，是指受力面角支撑点处承
受拉力的钢材筋之间的应力，称为压应力。

第6章梁的应力分析与强度计算梁是一种常见的结构构件，在建筑、桥梁、机械等领域都有广泛的运用。

在使用梁时，需要对其进行应力分析与强度计算，以确保其安全运行。

本章将介绍梁的应力分析与强度计算的基本原理和方法。

1.梁的应力分析梁的应力分析是指对梁内部各点的应力状态进行分析。

应力是指单位截面上受力的大小，常用的应力有轴力、弯矩和剪力。

对于梁的应力分析，主要有两个基本的方程：平衡方程和应变-位移关系。

1.1平衡方程平衡方程是指在梁内力平衡的条件下，梁内部各点的受力平衡。

对于梁来说，平衡方程可以表示为：∑Fx=0∑Fy=0∑M=0其中，∑Fx和∑Fy分别表示横截面上各点受力在X和Y方向的合力，∑M表示横截面上各点受力对横截面上其中一点产生的力矩。

通过求解平衡方程可以得到梁内力的分布情况。

1.2应变-位移关系应变-位移关系是指梁内部各点的应变与位移之间的关系。

梁的应变可以分为轴向应变、横向应变和剪应变三种，位移则可以分为平移位移和旋转位移。

应变-位移关系可以表示为：εx = du/dxεy = dv/dyγxy = (dudv + dvdx)/2其中，εx和εy分别表示横截面上各点的轴向应变，γxy表示横截面上各点的剪应变，du和dv分别表示横截面上各点的位移在X和Y方向上的微分。

2.梁的强度计算梁的强度计算是指根据应力分析的结果，对梁的强度进行评估。

梁的强度主要包括弯曲强度、剪切强度和扭转强度。

2.1弯曲强度弯曲强度是指梁在受到弯矩作用时的抗弯承载能力。

根据弯曲的理论，可以得到梁的最大正应力和最大剪应力。

对于矩形截面的梁来说，最大正应力和最大剪应力可以分别表示为：σmax = M * y / Iτmax = T * Q / It其中，M表示弯矩，y表示梁离中性轴的距离，I表示梁的惯性矩，T表示剪力，Q表示横截面的剪力传递量，It表示横截面的扭转惯性矩。

2.2剪切强度剪切强度是指梁在受到剪力作用时的抗剪承载能力。

梁的应力公式梁是工程结构中常见的构件，比如桥梁的大梁、房屋的横梁等等。

要了解梁的性能和安全性，就得搞清楚梁的应力公式。

先来说说啥是应力。

应力就好比是梁内部的“力量分布”，它反映了梁在受力时内部各点的受力强度。

想象一下，一根梁被重物压着，它内部的每一部分都在努力抵抗这个压力，而应力就是描述这种抵抗强度的指标。

梁的应力公式有好几种，咱们先从最简单的说起。

对于矩形截面的梁，在受到垂直于轴线的弯矩作用时，正应力的公式是：σ = M*y / I 。

这里的σ就是正应力，M 是弯矩，y 是所求应力点到中性轴的距离，I 是截面惯性矩。

举个例子吧，有一次我去一个建筑工地，看到工人们正在搭建一个厂房的框架。

其中有一根大梁，看上去很粗壮，但我心里就在想，这根梁到底能不能承受住上面的重量呢？这时候我就想到了梁的应力公式。

我走近仔细观察了一下这根梁的截面形状，大致估计了一下它的尺寸。

然后假设上面的重物产生了一个特定大小的弯矩，根据我所知道的公式和估计的参数，试着算了算梁内部的应力分布。

这一算可不得了，我发现如果重物再重一点，或者放置的位置再偏一点，某些部位的应力可能就会超过材料的承受极限，那可就危险啦！再来说说圆形截面的梁。

它的应力公式和矩形截面的有所不同，但原理是类似的。

对于圆形截面，应力的计算也要考虑到弯矩、到圆心的距离以及截面的惯性矩等因素。

在实际工程中，梁的受力情况往往很复杂，可能同时受到弯矩、剪力、扭矩等多种力的作用。

这时候，就得综合运用各种应力公式来进行分析。

比如说，在设计一座钢结构的桥梁时，工程师们不仅要考虑车辆行驶时产生的弯矩，还要考虑风力、地震力等因素产生的影响。

他们会运用先进的计算软件，输入各种参数，然后根据梁的应力公式来计算出每一个部位的应力情况。

如果发现某些部位的应力过大，就需要调整设计，比如增加梁的截面尺寸、改变材料或者优化结构形式。

总之，梁的应力公式是结构工程中的重要工具，它帮助我们设计出安全可靠的梁结构，确保建筑物和各种设施的稳定和安全。

eBook材料力学习题详细解答教师用书(第6章)2008-8-8范 钦 珊 教 育 教 学 工 作 室FAN Qin-Shan’s Education & Teaching Studio习题6－1 习题6－2 习题6－3 习题6－4 习题6－5 习题6－6 习题6－7 习题6－8 习题6－9 习题6－10 习题6－11 习题6－12 习题6－13 习题6－14 习题6－15 习题6－16 习题6－17 习题6－18 习题6－19 习题6－20材料力学习题详细解答之六第6章 梁的应力分析与强度计算6－1 悬臂梁受力及截面尺寸如图所示。

图中的尺寸单位为mm 。

求：梁的1－1截面上A 、B 两点的正应力。

解：1。

计算梁的1－1截面上的弯矩：31m 110N 1m+600N/m 1m 1300N m 2M ⎛⎞=−××××=−⋅⎜⎟⎝⎠ 2。

确定梁的1－1截面上A 、B 两点的正应力：A 点：()336-3-315010m 1300N m 2010m 210Pa MPa ()10010m 15010m12z A z M y I σ−−⎛⎞×⋅×−×⎜⎟⎝⎠==×=××× 2.54拉应力 B 点：()3363-3-315010m 1300N m 4010m 216210Pa 162MPa ()10010m 15010m12..z A z M y I σ−−⎛⎞×⋅×−×⎜⎟⎝⎠===×=×××压应力6－2 加热炉炉前机械操作装置如图所示，图中的尺寸单位为mm。

其操作臂由两根无习题6－2图习题6－1图缝钢管所组成。

外伸端装有夹具，夹具与所夹持钢料的总重F P ＝2200 N ，平均分配到两根钢管上。

求：梁内最大正应力（不考虑钢管自重）。