第二章-复变函数

复变函数第二章学习指导一. 知识结构1.复变函数在一点可导的定义2.解析函数 2.42.53.15⎧⎧⎨⎪⎩⎪⎪⎧⎪⎨⎨⎩⎪⎪⎧⎪⎨⎪⎩⎩函数在一点解析的定义定义函数在区域解析的定义四则运算运算复合运算定理充分必要条件定理及定理 3.初等函数(),,sin ,cos ,,z z z e z z Lnz z a z a αα⎧⎪⎨⎪⎩n 单值函数:z 与有例外 二. 学习要求⒈理解解析函数的定义，性质及其充分必要条件；⒉了解函数在一点解析与函数在一点可导的区别；⒊熟练掌握利用柯西——黎曼条件判别解析函数的方法；⒋熟练掌握“已知解析函数的实部（或虚部），求该解析函数”的方法.5.理解z z sin ,e 与z cos 的定义及其主要性质；6.,,z Lnz z a α的定义及其主要性质.三. 内容提要1.函数在一点可导的定义是设函数)(z f w =定义在区域D 内，D z z D z ∈∆+∈)(,00，若z z f z z f z ∆-∆+→∆)()(lim 0存在，则称此极限为函数)(z f 在点0z 的导数，记为)(0z f '，即 zz f z z f z f z ∆-∆+='→∆)()(lim )(0000 此时，称函数)(z f 在点0z 可导，否则，称函数)(z f 在点0z 不可导.2.函数在一点解析的定义是设函数)(z f w =定义在区域D 内，0z 为D 内某一点，若存在一个邻域),(0p z N ，使得函数)(z f 在该邻域内处处可导，则称函数)(z f 在点0z 解析.此时称点0z 为函数)(z f 的解析点.若函数)(z f 在点0z 不解析，则称0z 为函数)(z f 的奇点.关于解析函数的定义，有下面的注解：注解1 解析性与可导性：在一个点的可导性是一个局部概念，而解析性是一个整体概念；注解2 函数在一个点解析，是指在这个点的某个邻域内解析，因此在此点可导；反之，在一个点的可导性不能得到在这个点解析.3.若函数),(i ),()(y x v y x u z f ++=定义在区域D 内，则函数)(z f 在区域D 内为解析函数的充分必要条件是：⑴),(y x u 与),(y x v 在D 内可微.⑵x y y x v u v u -==,在D 内成立.条件⑵称为柯西——黎曼条件或C.— R.条件.函数)(z f 在区域D 内为解析函数的充分必要条件是：⑴y x y x v v u u ,,,在D 内连续．⑵x y y x v u v u -==,在D 内成立．关于柯西-黎曼条件，有下面的注解：注解1 解析函数的实部与虚部不是完全独立的，它们是C-R 方程的一组解； 注解2 解析函数的导数形式更简洁.4.初等解析函数整幂函数定义 设y x z i +=，n 为正整数，称n z w =为整幂函数．指数函数定义2.4 设y x z i +=，称)sin i (cos e e y y x z ⋅+=为指数函数，其等式右端中的e 为自然对数的底，即 2.71828e =． ⑴对任意二复数111i y x z +=与222i y x z +=,有2121e e e z z z z +=⋅⑵z e 在复平面上为解析函数，且有z z e )(e ='⑶对任意一复数y x z i +=，有 π2)(Arg ,e e k y z x z +== （k 为整数）⑷z e 只以i π2k (k 为整数)为周期．⑸21e e z z =的充分必要条件是i π212k z z =- （k 为整数）⑹z z e lim ∞→不存在． ⑺设y x z i +=，若0=y ，则x z e e =；若0=x ，则y y y sin i cos e i ⋅+=这便是欧拉公式．⑻若y x z i +=，则zz e e =．三角函数定义2.6 设z 为复数，称i 2e e i i zz -- 与2e e i i z z -+ 分别为z 的正弦函数和余弦函数，分别记作i2e e sin i i zz z --= 与 2e e cos i i z z z -+= 正.余弦 函数的性质：⑴z sin 与z cos 在复平面解析，且有z z z z sin )(cos ,cos )(sin -='='⑵三角学中实变量的三角函数间的已知公式对复变量的三角函数仍然有效：例如，由定义可推得1cos sin 22=+z zz z cos )2sin(=+π z z sin )2cos(-=+π212121sin cos cos sin )sin(z z z z z z ±=±212121sin sin cos cos )cos(z z z z z =±z z sin )sin(-=-z z cos )cos(=-⑶z z z i e sin i cos =+⑷z sin 仅在πk z =处为零，z cos 仅在π2πk z +=处为零，其中的k 为整数． ⑸z sin 与z cos 均以π2k （k 为整数)为周期； ⑹命题“若z 为复数，则1cos ,1sin ≤≤z z ”不真．⑺z z sin lim ∞→与z z cos lim ∞→均不存在． 同理可以定义其他三角函数：sin cos tan ,cot ,cos sin 11sec ,csc .cos sin z z z z z z z z z z ====5.初等多值函数.根式函数定义2.9 设)0(e i ≠=θr z ，称满足z w n = （n 为不小于2的正整数）的w 为z 的n 次根式函数，或简称根式函数，记作n z w =⑴根式函数为多值函数，它不是解析函数．对于每一个确定的)0(e i ≠=θr z ，都有n 个不同的w 与之对应，即有n n r w θi 0e =n n r w π2i 1e +=θ … n n n n r w π)1(2i 1e -+-=θ因为根式函数是多值函数，所以，它不是解析函数．⑵根式函数在从原点起沿正实轴剪开的复平面上可分出n 个单值函数．定义 设函数)(z F w =为多值函数，若当变点z 从起始点0z 出发绕一条包围点a 的简单闭曲线连续变动一周再回到起始点0z 时，函数)(z F 从一个支变到另一个支，则称点a 为函数)(z F 的支点．⑶根式函数n z w =的每个单值支在从原点起始沿正实轴剪开的复平面上为解析函数．对数函数定义2.10 设∞≠,0z ，称满足z w =e的w 为z 的对数函数，记作z w Ln =注解1.由于对数函数是指数函数的反函数，而指数函数是周期为i π2的周期函数，所以对数函数必然是多值函数；注解2.Lnz ln|z|iArg 0w z,z ==+≠.多值函数的单值化：1）由于Ln ln ||z z iArgz =+，而是Argz 通常正数的自然 对数，Arg z 是多值函数，所以对数函数的多值性是由于辐角函数的多值性引起的，每两个函数值相差2i π的整数倍；2）像rg A z 一样，取主值arg z ，则得到Lnz 的一个单值分支，记为lnz ，也称为Lnz 的主值，即ln ln arg z z z =+令v u w z r z i ,,0,e i +=∞≠=θ由定义2.10可得z w Ln =)π2(ln k i r ++=θz i z Arg ln += （k 为整数）即对于每一个∞≠,0z ，有无穷多个不同的w ，即有)π4(i ln 2k z w ++=θ)π2(i ln 1k z w ++=θθi ln 0+=z w)π2(i ln 1k z w -+=-θ)π4(i ln 2k z w -+=-θ与之对应，因此，对数函数为多值函数，从而，它不是解析函数． 一般幂函数定义：利用对数函数，可以定义幂函数：设a 是任何复数，则定义z 的a 次幂函数为Ln a a z z e =当a 为正实数，且0z =时，还规定0a z =.一般幂函数的基本性质：（1）由于对数函数的多值性，幂函数一般是一个多值函数；（2）当a 是正整数时，幂函数是一个单值函数；（3）当1a n=（当n 是正整数）时，幂函数是一个n 值函数； （4）当p a q=是有理数时，幂函数是一个q 值函数； （5）当a 是无理数时，幂函数是一个无穷值多值函数反正切函数：由函数w z tan =所定义的函数w 称为z 的反正切函数，记作z w Arctan =，由于iw iw iwiw ee e e i z --+-=1， 令τ=iw e 2，得到111+-=ττi z ， 从而 i z i z ++-=τ， 所以])(Ln )([Ln 21Ln 21Arctan πi i z i z i iz i z i z w ++--=++-==反正切函数是多值解析函数，它的支点是i z ±=，无穷远点不是它的支点.四. 疑难解析解析函数概念1．函数()f ω=z 在一点0z 可导与解析有什么不同？在一个区域D 呢？ 答：函数()f ω=z 在一点0z 解析比可导的要求要高的多.)(z f 在0z 解析，要求)(z f 不仅在0z 可导，还要求在的邻域内也可导.例如，函数()f =z zRe(z)在z =0可导（导数等于零），但在除去原点的全平面都不可导（因为[]Re()Re()Re()ω=-+ z z +z z z +z z z在→ z 0时，没有确定的极限），所以，)(z f 在z =0不解析.在一个区域D 内，因为所有点都是内点，所以()f ω=z 在D 内可导与在D 内解析是一致的.2．复变函数()f ω=z 的导数定义与实一元函数()y f x =的导数定义在要求上有什么不同？答: 两者在定义的形式与求导公式.求导法则上都完全相同.但是由于极限的要求不同，在复变函数()f ω=z 的导数定义()()lim f f →- 00z 0z +z z z中，0z ∆→的方式是任意的，而实一元函数()y f x = 定义中，0x ∆→的方式要简单的多.所以，我们说复变函数在一点可导的条件更为严格，从而复变函数的导数具有不少特殊的性质.3．判别函数可与解析有哪些方法？答: 目前为止，可用以下三种方法.（1）由定义判别.若()f ω=z 在0z 可导，且在0z 邻域内可导，则在解析.)(z f 在0z 导数存在，则在0z 可导；在0z 导数不存在，则0z 是)(z f 的奇点.（2）由定理1判别)(z f 在点z 是否可导.考察两个实二元函数(,)u x y 与(,)v x y 在点(,)x y 内是否可微，并验证是否满足柯西—黎曼条件（简称C —R 条件）.（3）用定理2判别)(z f 在D 内是否解析.考察两个实二元函数(,)u x y (,)v x y 在D 内是否可微，并验证是否满足C —R条件.常常有人忽略对与(,)v x y 可微的考察而导致错误.例如()f =z 个坐标轴上函数都等于零，所以在z =0处，有0u u v v x y x y ∂∂∂∂====∂∂∂∂ （()0,0(0,0)0lim lim 0x u x u u x x x→-∂===∂ 其他类似可求），即(,)u x y 与(,)v x y 在点(0,0)满足C —R 条件，但)(z f 在z =0不可微，所以在点(0,0)，)(z f 不解析（因为ω= z ，取x αγ=，y βγ=，则当0γ→时ω→ z 随,αβ的取值而改变，不惟一）.4 复变函数的连续.可导（可微）与解析之间有什么关系？答: 由于()f ω=z 在一点可导与解析不同，所以，对定义在D 上的函数)(z f 及点D ∈0z ，)(z f 的()f ω=z 连续.初等函数1.叙述复变函数与实变指数函数的区别.答: 由于exp (cos sin )x e y i y =+z z =e ，其区别为(1) 0≠z e ，而0x e >；(2) i π=z z+2k e e 是以2k i π为周期的周期函数，而x e 不是周期函数；(3) z e 没有乘幂的意义，而x e 可视为e 的x 次幂；(4) 0→z z lim e 不存在，而0x →-∞=x lim e ，x →+∞=+∞x lim e . ２.怎样区分e 的z 次幂与z e ？答: 由题1知，z e 没有乘幂的意义，它是单值的，而e 的z 次幂是一个多值函数，为了区别，记为⎡⎤⎣⎦z e ,[]exp()exp{}π⎡⎤==⎣⎦z e zlne z lne+i(0+2k ) []exp exp exp(ππ==⋅z(1+2k i)z 2k i)当0k =或0k ≠，z 为整数时，exp ⎡⎤=⎣⎦z e z .当0k ≠时，q z =p与exp z 的模相等，辐角不同. 当0k ≠，z 为无理数时，两者模相等，辐角不同.当0k ≠，z 为纯虚数时，两者模不等，辐角相同.当0k ≠，z 为复数时，两者模一般也不相同.３.exp z z =e 什么时候等于实数？答: 因为exp (cos sin )y i y +x z =e ，所以应有sin 0y ⋅=x e .而0≠x e ，故由 sin 0(0,1,).y y k k π=⇒==±⋅⋅⋅即当z 位于实轴且与实轴距离为k π的直线上时，x e 的值为实数.4. 叙述复变对数函数与实变对数函数的区别答: 因为ln ln 2k i π=+z z ，所以区别为：（1）ln z 是多值函数，ln x 是单值函数.（2）ln()ln ln =+1212z z z z ，ln()ln ln .=-1122z z z z 虽然与实对数函数运算法则相同，但意义不同.复变对数函数等式的意义是全体值的相等，而不是对应分支的相等.（3）1ln ln ln n n≠≠n z z,z.例如，对ln 2z ，当θi z =re 时，θ22i2z =r e ， 2ln ln (22),0,1,,r i m m θπ=++=±⋅⋅⋅2z 2ln 2ln (24),0,1,.r i k k θπ=++=±⋅⋅⋅z 显然两者实部相等，但虚部可取值却不相同.（4）ln z 的定义域为除零之外的全体复数，而ln x 的定义域是0x >.5．为什么sin 1≤z 与1≤cosz 在复数范围内不再成立？答: 因为sin ()i i e e --z z 1z =2i，所以 sin ()i i i i e e e e ---==-z z z z 1z 2i2ii i y y e e e e --=-=-z z 1122 当y =+∞时，0y e -→，y e →+∞，所以sin 1≤z 不再成立.同理可证，不再 有cos 1≤z .又sin sin()sin x y xchy icoxchy +z =+i =，而()y y chy e e -=+12， 1()2y y shy e e i-=-,当y →∞，chy 与shy →∞，所以sin 1≤z 不再成立. 平面场1.为什么要在无源又无旋的平面场上导轮复势函数？答： x A divA=y A x y∂∂+∂∂称为向量场A 的散度，divA 0≡的向量场称为管量场，即无旋场.divA>0称源，divA<0称沟（汇）.yA rotA=x A x y ∂∂+∂∂称为向量场A 的旋度.rotA=0的向量场称为势量场，即无旋场.无源又无旋的场，称为调和场，满足divA rotA 0≡≡.单连通域上的调和场是一个有势场.A 的势函数为v ，0v v =-. 使0A(x,y)=grad 0v .A 的力函数为u ，使1grad y x A A i A j u =-+=.u 和v 都是调和函数，且(,)v x y 是(,)u x y 的共轭调和函数.在单连通区域内，用势函数(,)u x y 和力函数(,)v x y 可以构造一个解析函数()(,)(,)f u x y iv x y ω==+z ，ω称为复势函数（简称复势）.讨论复势就是讨论一个解析函数.2.为什么在不同问题中场的复势表示有不同的形式？答: 因为在不同的物理应用中，为了各自的方便对复势采用了不同的定义，因而复势表示有不同的形式.如（1）在平面流速场(,)(,)x y v v x y i v x y j =+，有d (,)=-y x x y v dx v dy ϕ+, d (,)=-y x x y v dx v dy ϕ+.复势函数为()(,)(,)f x y i x y ωϕφ==+z ，______'()x y v v iv i i f x y x xϕϕϕφ∂∂∂∂=+=+=-=∂∂∂∂z （2）在平面静电场x y E E i E j =+，有(,)y x du x y E dx E dy =-+, (,)x y dv x y E dx E dy =-+复势函数为()(,)(,)f u x y iv x y ω==+z ,场E 何以用复势表示为______'()v u E i if x x∂∂=--=-∂∂z （3）在稳定状态的平面热流场，与题（2）类似______()()()d q k i k i k x y x x d ϕϕϕφ∂∂∂∂Φ=-+=--=-∂∂∂∂z 这里(,)(,)x y i x y ϕφΦ+(z)=称为复温度.五．典型例题例1 试证：函数)Re()(z z f =在复平面上处处不可导.分析：导数是一个特定类型的极限，要证明复变函数在某点的极限不存在，只需要找两条特殊的路径，使自变量沿这两条路径趋于该点时，函数值趋于不同的值.证 对任意点z ，因 zz z z z z f z z f ∆-∆+=∆-∆+)Re()Re()()( 令y x z ∆+∆=∆i ，于是有 yx x z z f z z f ∆+∆∆=∆-∆+i )()( 由于上式当z z ∆+沿平行于虚轴的方向趋于点z 时（即0,0→∆=∆y x ），其极限为0；当z z ∆+沿平行于实轴的方向趋于点z 时（即0,0→∆=∆x y ），其极限为1，所以zz f z z f z ∆-∆+→∆)()(lim不存在，故)(z f 在点z 处不可导.由点z 的任意性，函数)Re()(z z f =于复平面上处处不可导.例2 试证函数1)(+=z z f 在复平面解析． 证 令y x z v u z f i ,i )(+=+=，则 1i 1)(++=+=y x z z f y x i 1++= v i u += 于是1+=x u y v = 从而有0,1==y x u u 1,0==y x v v显然，y x y x v v u u ,,,在复平面上处处连续，且满足C.— R.条件，故函数)(z f 在复平面解析.函数)(z f 在区域D 内为解析函数的充分必要条件是)](Im[z f 为)](Re[z f 的共轭调和函数.例 3 设222),(y xy x y x u --=，试求以),(y x u 为实部的解析函数),(i ),()(y x v y x u z f +=，使得i )0(=f ．解 依C.— R.条件有y x u v x y 22-== 于是⎰-=y y x v d )22( )(22x y xy ϕ+-= 由此得)(2x y v x ϕ'+= y u -= y x 22+= 从而有c x x +=2)(ϕ 因此c x y xy y x v ++-=222),( （c 为任意常数） 故得)2(i 2)(2222c x y xy y xy x z f ++-+--= c z i )i 1(2++= 将i )0(=f 代入上式，得i c f ==i )0( 由此得1=c ，故得i )i 1()(2++=z z f 经验证，所得)(z f 既为所求.例4 试证zz e 1e =-． 证：设y x z i +=，由定义得及（实）三角函数的性质得 )]sin(i )[cos(e e y y x z -⋅+-=-- xyy e sin i cos ⋅-=)sin i (cos e )sin i )(cos sin i (cos y y y y y y x⋅+⋅+⋅-=)sin i (cos e sin cos 22y y yy x ⋅++=ze 1=. 例5 计算)i 1(Ln +．解：)i 1(Arg i i 1ln )i 1(Ln +++=+)π24π(i 2ln 21k ++=（k 为整数） 例6 试证z z z i 2i e sin i 21e =-. 证：由定义zz z z z i 2i i i e i 21e i 2e e sin -=-=- 可得z z z i 2i e sin i 21e =-.例7 计算)i 1cos(+的值．解 由定义得2e e 2e e )i 1cos(1i 1i )i 1(i )i 1(i +--+-++=+=+1sin )e e (21i 1cos )e e (2111-++=--. 例8设)(z f 在区域D 内解析，证明：若)(z f 满足下列条件之一，则)(z f 在D 内为常数：（1）对每一个∈z D ，有)(z f =0, （2）)(Re z f 或)(Im z f 在D 内为常数, （3）)f(z 在D 内为常数, （4）)(z f 在D 内解析, （5）)(z f 恒在D 内为实数, （6）)(arg z f 在D 内为常数, （7）2u v =,（8）c bu au =+,其中c b a ,,是不全为零的常实数.证明：（事实：在区域D 内，0====y x y x v v u u ,则在D 内，v u ,为常数） （2）设iv u z f +=)(,因为()z f 在D 内为解析，所以(),(1)u v u vx y y x∂∂-∂-∂==-∂∂∂∂()()()2,xu y u y u x u D iv u f z ∂-∂-=∂∂∂∂=∂∂+=内解析，所以也在又()()()内为常数在故得由D z f y v x v y u x u ，021=∂∂=∂∂=∂∂=∂∂（8）因为au+bv=c 且a,b 与c 不全为零，所以a 与b 不能同时为零.否则，若a=b=0，则c=0.不妨设a ≠0，则于是有),(1bq c au -=()()(),,1,20,,,()u b v x a x u b v y a y f z u iv D u v u u x y y xu u v vx y x y u v f z D ∂∂⎧⎫=-⎪⎪∂∂⎪⎪⎨⎬∂∂⎪⎪=-∂∂⎪⎪⎩⎭=+∂∂∂∂==-∂∂∂∂∂∂∂∂====∂∂∂∂又因为在内解析所以由可得因此均为常数即在内为常数.例9．讨论函数i y x y x z f 22332)(+-=的可导性和解析性，并在可导处求导数22332),(,),(y x y x y x y x u ：=-=θ令解, y x xy y u x u y x y x 22224,4,3,3==-==θθ 显然上述四个偏导函数在z 平面上连续. 要使x y y x u u θθ-==,, 即222243,43xy y y x x -=-=,即⎪⎪⎩⎪⎪⎨⎧==⎩⎨⎧==4343,00y x y x . 故处可导43430)(i z f +与在.在平面上不解析.)1(1627|)43()4343('0|)43(|)()('4343220220i xy i x i f xy i x i u o f i z z x x +=+=+=+=+=+==ϑ. 例10.试证()31)(z z z f w -==在割破0到1的直线段以及负虚轴的z 平面上，可以分成单值解析分支，且求出的0)2(<f 那个分支中)(i f 的值解：∞,1,0)()(的可能支点为z f i ,因3+1，3+（1+1）∞∴,1,0都是支点. 所以在割破0到1的直线段以及负虚轴的z 平面上可以分出三个单值解析分支()(2)0,arg (2),ii f f π<= 故可取而()πππ12543231)1arg(arg 31)(arg =⎪⎭⎫ ⎝⎛+=-∆+∆=∆z c z c z f c ()()()i i i eee i i i if 125612531321)(πππ-=⋅--=∴.例11.试证：在将z 平面适当割开后，函数 32)1()(z z f -=能分出三个单值解析分支，并求出在点z=2取值的那个分支在i z =的值解：())(z f i 的可能支点为。

第二章 习题解答提示（一）1.（定理）设连续曲线[]βα,),(:∈=t t z z C ，有[]),(0)(00βα∈≠'t t z ，则（试证）曲线C 在点)(0t z 有切线。

分析 1）在)(0t z 的某去心领域内能联结割线()(10t z t z ； 2）割线的极限位置就是切线。

证1）,0>∃δ使}{\),(0001t t t t δδ+-∈∀，有)()(01t z t z ≠，即C 在)(0t z 的 对应去心领域内无重点，即能够连接割线()(10t z t z ，否则就存在数列{},01t t n →使)()(01t z t z n =。

于是0)()(lim )(0101001=--='→t t t z t z t z n n t t n ，这与假设矛盾。

2）01001),(t t t t t >⇒+∈δ，[],)()(arg )()(arg010101t z t z t t t z t z -=--[])()(arg lim 010t z t z t t -∴→（对)(0t z 割线)()(10t z t z 倾角的极限）⎥⎦⎤⎢⎣⎡--=--=→→01010101)()(lim arg )()(arglim 0101t t t z t z t t t z t z t t t t )(a r g0t z '=。

因此,割线确实有极限位置,即曲线C 在点)(0t z 的切线存在,其 倾角为)(arg 0t z '.3. 设 ⎪⎩⎪⎨⎧=≠+==+++-.0,0;0,)(223333)(z iy x z z f y x y x i y x试证)(z f 在原点满足..R C -条件,但却不可微. 证 1) 有公式(2.5)及(2.6)有;1)0()(lim0i z f z f iv u x y x x +=-=+→=.1)0()(lim0+=-=+-→=i zf z f v iu y x y y2) 但z 当沿直线0)0(→≠=m mx y 时,zf z f z )0()(lim-→随m 而变.4. 试证下列函数在z 平面上任何点都不解析: (1) z ; (2) y x +; (3) z Re ; (4)z1. 分析 由于孤立的可微点不是解析点,故只须证明各函数 个别点外处处不满足解析的必要条件:..R C -条件.证 (1) 当0≠z 时,即y x ,至少有一0≠时,或有,y x v u ≠ 或有.x x v u -≠故z 至多在原点可微;(2) 在上处处不满足..R C -条件;(3) 的结论同(2); (4),122y x iy x zz z z ++==除原点外,..R C -条件处处不成立. 5. 判断下列函数的可微性和解析性: (1) ;)(22y ix xy z f += (2) ;22iy x +(3) ;32)(33iy x z f += (4) ).3(33223y xy i xy x -+- 分析 如只在孤立点或只在直线上可微,都未形成由可微点构成的圆邻域,故都在其上不解析;利用推论2.3考查可微性,然后应用解析的定义.解 (1) .),(,),(22y x y x v xy y x u == 仅当0==y x 时,22,22xy v u xy x v u y x y y x -=-=====且此四偏导数在原点连续,故)(z f 只在原点可微,且.0)2()()0()0,0(2)0,0(===+='xyi x iv u f x x6. 若函数)(z f 在区域D 内解析,且满足下列条件之一,试 证)(z f 在D 内必为常数.(1) 在D 内;0)(='z f (2))(z f 在D 内解析; (3) )(z f 在D 内为常数;(4) )(Re z f 或)(Im z f 在D 内为常数. 分析 分别由各题设条件及..R C -条件得:在D 内,0====y x y x v v u u 从而v u ,在D 内为常数.引理* 在区域D 内0====y x y x v v u u(A)⇒在D 内v u ,为常数.事实上,1) 设000iy x z +=为D 内一定点.)(00y y i x x iy x z ∆++∆+=+=是D 内任一点.若这两点能用全含于D 内的直线段z z 0来联结, 则有:),(),(0000y x u y y x x u u -∆+∆+=∆ x y y x x u x ∆∆+∆+=),(00θθ).10(),(00<<∆∆+∆++θθθy y y x x u y )(B这是因为,”若令),10(,00≤≤∆+=∆+=t y t y y x t x x 则有),,()(00y t y x t x u t F ∆+∆+= x y t y x t x u t F x ∆∆+∆+='),()(00 .),(00y y t y x t x u y ∆∆+∆++而.,y dtdy x dt dx ∆=∆= 由数学分析中的微分中值定理得)()01)(()0()1(θθF F F F '=-'=-).10(<<θ于是)(B 式成立.”从而由)(A 知,0=∆u 即),(),(00y x u y x u =.即在D 内u 为常数.同理,在D 内v 为常数.2) 若联结两点0z 与z 的直线段不全含于D 内,由区域的连通性知,可用全含在D 内的折线段将0z 与z 连接.若111iy x z +=是折线上0z 后面的一个顶点,则在)1段中u ∆的表达式)(B 中, 令,1010,y y y x x x =∆+=∆+立即得).,(),(0011y x u y x u =如此逐步推算,由一顶点至另一顶点,最后可得()().,,00y x u y x u =即在D 内u 为常数. 同理,在D 内v 为常数.引理*证毕. 证(1)...)(0,y y x x iu v R C iv u z f D iy x z --+='=∈+=∀(2) 由题设条件iv u +及iv u -在D 内解析,再由..R C -条件可推得0====y x y x v v u u 最后有引理*可得证.(3) 由题设,在D 内=)(z f 常数C . 1) .0)(0≡⇒=z f C 2) .0)(0≠⇒≠z f C证一 )()()(2z f C z f C z f =⇒=在D 内解析,于是由题(2)得知D z f 在)(内为常数.证二 ,0222≠=+C v u 分别对y x ,微分,再应用..R C - 条件,讨论解二元一次方程组,即得在D 内.0====y x y x v v u u(4) 由..R C -条件推得,在D 内.0====y x y x v v u u 8. 试证下列函数在z 平面上解析,并分别求出其导函数. (1) ;33)(3223i y xy yi x x z f --+=(2) );sin cos ()sin cos ()(y x y y ie y y y x e z f xx ++-= (3) ;cos sin )(xshy i xchy z f += (4) ;sin cos )(xshy i xchy z f -= 证 应用定理2.5及求导公式(2.7).),2cos(2sin 21sin )cos()cos(cos nb a b bn nb a b a a ++=+++++ (1)及).2sin(2sin 21sin )sin()sin(sin nb a b bn nb a b a a ++=+++++ （2）证一 分别证明（1）和（2）.按定义将正,余弦函数表成指数函数,再等比级数求和的公式简化.注 由于a 和b 是复数,不能从(1)+i (2)着手化简后,再比较实,虚部. 证二 先将(1)和(2)式两端各乘2sin b去分母后,再应用三角函数中积化和差的公式,代入左端化简.16. 试证：（1）ishz iz =)sin(；（2）chz iz =)cos(；（3）z i iz sh sin )(=；（4）z iz ch cos )(=； （5）ithz iz tg =)(；（6）itgz iz th =)(.证 （1）、（2）应用定义2.5及2.7；（3）由（1）；（4）由（2）；（5）、（6）由定义2.6、及2.7及（1）、（2）. 17. 试证：（1）122=-z sh z ch ；（2）1sec 22=+z th z h ；（3）212121)(shz shz chz chz z z ch +=+.证 （1）由16题（1）、（2）；（2）由本题（1）；（3）由16题（1）、（2）. 18. 若,iy x z +=试证：（1）xshy i xchy z cos sin sin +=； （2）xshy i chy z sin cos cos -=；（3）y sh x z 222sin sin +=； （4）y sh x z222cos cos +=.证 （1）、（2）应用16题（1）、（2）；（3）、（4）分别应用本题（1）、（2）及17题（1）. 20. 试解方程：（4）0sin cos =+z z ；（5）i tgz 21+=. 解 （4）.0)sin 21cos 21(2=+z zππk z +-=4（k 为整数）.（5）Arc z =)21(1)21(121)21(i i i i Lni i tg +-++=+=+-=5221i Ln i⎥⎦⎤⎢⎣⎡-+=21)12(21arctg k z π +).,1,0(5ln 4±=k i21. 设θi re z =，试证[])cos 21ln(21)1ln(Re 2θr r z -+=-. 证 设ϕρi e z =-1，则[]ρln )1ln(Re =-z .22. 设3z w =确定在从原点0=z 起沿正实轴割破了的z 平面上，并且i i w -=)(，试求)(i w -之值.解一 32)(3)()(πθk z ik ez r z w +=，（G z ∈：πθ2)(0<<z ；2,1,0=k ）1） 利用i i w -=)(定)2;2,=k k 求)(2i w -. 解二 作图2.0.13)(z z f =3arg 31)(arg π=∆=∆⇒z z f c c .再由公式（2.25）计算).)((6i ei f π-=-23. 设3z w =确定在从原点0=z 起沿负实轴割破了的z 平面上，并且32)2(-=-w （这是边界上岸点对应的函数值），试求)(i w 之值.解一 .,222ππii e i e ==-由32)2(-=-w 定,1,=k k 从而.)(651i ei w π=解二 作图2.0.2.3)(z z f =，而[].arg )2(arg 3π=-=-z f又∆ .6arg 31)(arg ,2arg ππ-=∆=∆-=z z f z c c 再应用公式（2.25）计算))((65i e i f π=.24. 已知1)(4+=z z f 在ox 轴上A 点（1>=R OA ）的初值为14++R ，令z 由A 起沿正向再以原点为中心的圆周上走41圆周而至oy 轴的B 点，问)(z f 在B 点的终值为何？分析 题设的函数1)(4+=z z f 是具有四个有限支点的二值函数，讨论起来比较繁难，而经过变数代换4z w =后，就简化成具有单有限支点-1的二值函数1+=w w .解 z 在z 平面上沿以0=z 为心，1>R 为半径的圆周c 从A 走到B ，经过变换4z w =，其象点w 在w 平面上w=0为心，14>R 为半径的象圆周Γ从'A 走到B '，刚好绕1+=w w 的交点-1转一整周.故它在B '的值为1+-w .因此1|)(|)(4+-=-=R z f z f A B . 25. 试证：在将z 平面适当割开后，函数32)1()(z z z f -=能分出三个单值解析分支.并求出在点2=z 取负值的那个分支在i z =的值.分析 仿例2.3.14，2.3.15及2.3.16解之.证 )(z f 的支点是,1,0=z 在沿]1,0[割开的z 平面的区域D 内，)(z f 能分出三个单值解析分支.证一 令11r z =-1θi e ，2r z = 2θi e当2=z 时，2,1,0,2121====r r θπθ.由已知π)(arg z f k 定1,=k k .然后计算i ei f 127612)(π-=32232121)]()[()(πθθk ik ez r z r z f ++=证二 作图2.0.4.由2到i ，取路线1C .,127)(arg 1π=∆z f c 再按公式（2.25）计算)(i f 证三 作图2.0.4.由2到I ,取路线2C ,π1217)(arg 2-=∆z f c .再按(2.25)计算)(i f .(二)1.设21)(z z z f -=,试证().1,0)()(Re <>⎥⎦⎤⎢⎣⎡'z z f z f z证2224221I m (2111)()(zz i z z z z f z f z -=-=-+='.2.设zzz f -=1)(,试证 ().1,0)()(1Re <>⎥⎦⎤⎢⎣⎡'''+z z f z f z 证3.若函数在上半平面内解析，试证函数在下半平面内解析. 证一设z z 、0分别为下半z 平面内的定点及动点，可证)()()(lim0000z f z z z f z f z z '=--→.由0z 的任意性及解析的定义得证.证二),(),()(y x iv y x u z f +=在上半平面)0(>y 内解析⇒1)),(),,(y x v y x u 在0>y 可微，且2)yy x v x y x u ∂∂=∂∂),(),(, )0(),(),(>∂∂-=∂∂y xy x v y y x u ()* 考查)0)(,(),()(<--=y y x iv y x u z f ，则可证：1)),(),,(y x v y x u ---在0<y 内可微，且由()*式有 2）[][]yy x v x y x u y ∂--∂*∂-∂>-),()(,)0(， [][]xy x v y y x u ∂--∂-=∂-∂),()(,. 4．(形式导数)(1)设二元函数),(y x u 有偏导数.此函数可以写成iy x z +=及z 的函数).2,2(izz z z u u -+= 试证(形式地)⎪⎪⎭⎫⎝⎛∂∂+∂∂=∂∂⎪⎪⎭⎫ ⎝⎛∂∂-∂∂=∂∂y u i x u z u y u i x u z u 21,21 (2)设复变函数),(),()(y x iv y x u z f +=,且),(y x u 和),(y x v 都有偏导数.试证(形式地):对于)(z f ,柯西—黎曼(Cauchy-Riemann)条件可以写成0=∂∂+∂∂=∂∂zvi z u z f (由此可见,解析函数是以条件0=∂∂zf为其特征的.因此,我们不妨说,一个解析函数与z 无关,而是z 一数的函数.)证 （形式地）（1）由于)(21),(21z z iy z z x -=+=. 这里视z z ,为两个独立变量.根据复合函数求偏导的法则，即可形式地得证。

第二章 复变函数的积分在微积分学中，微分法与积分法是研究函数性质的重要方法。

同样，在复变函数中，积分法也跟微分法一样是研究复变函数性质十分重要的方法和解决实际问题的有力工具。

§2.1 复变函数积分的概念一、复变函数的积分设C 为平面上给定的一条光滑(或按段光滑)曲线。

若选定C 的两个可能方向中的一个作为正方向，那么就把C 理解为带有方向的曲线，称为有向曲线。

设曲线C 的两个端点为A 与B ，如果从A 到B 的方向作为C 的正方向，那么从B 到A 的方向就是C 的负方向，并把它记作-C 。

在今后的讨论中，常把两个端点中的一个作为起点，另一个作为终点。

除特殊声明外，正方向总是指从起点到终点的方向。

关于简单闭曲线的正方向是指当曲线上的点P 顺此方向沿该曲线前进时，临近P 点的曲线内部始终位于P 点的左方。

与之相反的方向就是曲线的负方向。

若光滑或逐段光滑的曲线C 的参数方程为)()()(t iy t x t z z +==，)(βα≤≤t （2.1） t 为实参数，则规定t 增加的方向为正方向，即由)(αz a =到)(βz b =的方向为正方向。

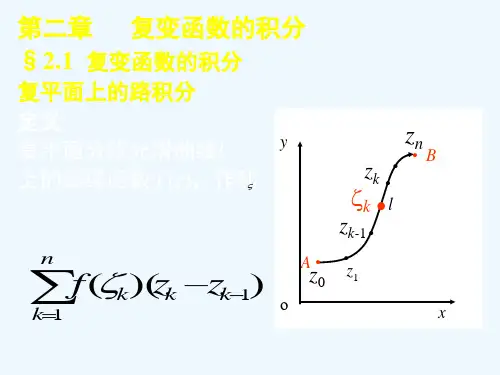
定义2.1 设函数)(z f w =定义在区域D 内，C 为区域D 内起点为A 终点为B 的一条光滑有向曲线，把曲线C 任意分成n 个弧段，设分点为：B z z z z z A n n ==-,...,,,1210 在每个小弧段上任取一点k ζ（图3.1），作和∑=∆=nk k k n z f S 1)(ζ其中1--=∆k k k z z z ，记=∆k s 的长度，}Δ{max 1k nk s δ≤≤=。

当n 无限增加，且δ趋于零时，如果不论对C 的分法及k ζ的取法如何，当n S 有唯一极限，那么称这个极限值为函数)(z f 沿曲线C 的积分，记作∑⎰=→=nk k kδCz ζf dz z f 1Δ)(lim )( （2.2）图2.1C 称为积分路径，⎰Cdz z f )(表示沿C 的正方向的积分，⎰-C dz z f )(表示沿C的负方向的积分。

Anhui University 在上一章学习了复变函数，重点介绍了解析函数的许多性质，这些性质都是在可导和可微的基础上得出的。

第2章复变函数积分()(,)(,) 若函数在区域内解析则有：f z u x y iv x y D =+1. 解析函数的调和性：解析函数的实部与虚部均满足二维拉普拉斯方程：（由C-R 条件可证明）。

220,0.xx yy xx yy u u u u v v v v ∆≡∇=+=∆≡∇=+=2. 解析函数的共轭性：解析函数的实部与虚部由C-R 方程联系，称为解析函数的共轭性。

具体说只要知道解析函数的实部或者虚部就可求得解析函数。

3. 解析函数的实部与虚部是彼此相互正交的曲线。

0),(),(=∇⋅∇y x v y x u为了深入理解复变函数，本章用积分理论来分析复变函数积分。

基本内容：1、掌握复积分的概念、性质和计算方法；2、掌握解析函数的基本定理－Cauchy定理及其应用；3、掌握解析函数的基本公式－Cauchy公式及其应用2.1 复数函数积分一. 复积分的定义1max 0()lim ()k n k k n C k z f z dz f z ζ→∞=∆→=∆∑∫记作：()w f z l =为被积函数，为积分路径。

二. 复积分存在的条件1max 0()lim ()k n k kn l k z f z dz f z ζ→∞=∆→=∆∑∫由上式可知：一个复积分的实质是两个实积分的和。

实积分存在的条件：(,)(,)分段光滑，，在上连续l u x y v x y l因此复积分存在的条件：分段光滑，在上连续。

()l f z l注1：所说的曲线总是指光滑或逐段光滑曲线。

注2：边界的正方向：规定当观察者沿曲线边界前进时，所围的区域始终在观察者的左手边，则前进的方向为正方向。

rzz<−单连通区域Rzzr<−<复连通区域正方向正方向三. 复积分的性质(1)()d ()d l lf z z f z z −=−∫∫反转积分路径：(2)()d ()d ;() l l kf z z k f z z k =∫∫为复常数(3)[()()]d ()d ()d ;l l l f z g z z f z z g z z ±=±∫∫∫121()(),,k n n k L l f z dz f z dz n l l l ==∑∫∫"（4），若曲线L由段线段组成被积函数的线性可叠加性积分路径的可叠加性(5)|()||()|||L L f z dz f z dz ≤⋅∫∫(6) , () () ()d ()d .设曲线的长度为函数在上满足那么l l l L f z l f z M f z z f z s ML ≤≤≤∫∫积分估值定理四. 计算方法1. 用定义计算2. 通过计算实积分结果表明：被积函数与积分路径有关。

第二章 复变函数:第二节：初等函数1、指数函数：我们要把实指数函数的定义扩充到整个复平面上，使得复变数z=x+iy 的函数f (z )满足下列条件：（1）x e x f R x =∈∀)(,；（2）f (z )在整个复平面C 上解析；（3）C ,21∈∀z z ，有)()()(2121z f z f z z f =+； 则可以证明，)sin (cos )(y i y e z f x +=，事实上，由(3)及(1)有)()()(iy f e iy x f z f x =+=令 ),()()(y iB y A iy f +=其中A (y )及B (y )是实值函数，所以)()()(y B ie y A e z f x x +=显然，y y A cos )(=及y y B sin )(=满足上面的条件。

若,,222111iy x z iy x z +=+=则有)()]sin()[cos()sin (cos )sin (cos )()(2121212211212121z z f y y i y y e y i y e y i y ez f z f x x x x +=+++=++=+ 因此，定义复指数函数，为)sin (cos exp y i y e z e w x z +==由此有Euler 公式：y i y e iy sin cos +=；指数函数的基本性质：（4）C ∈∀z ，0≠z e ；（5）指数函数z e w =在整个复平面内有定义并且解析，z z e e =)'(，指数函数z e w =是实指数函数在复平面上的解析推广；（6）Euler 公式：y i y e iy sin cos +=；（7）从定义得||x z e e =， ,2,1,02±±=+=k k y Arge z ，π利用Euler 公式，得到复数的指数表示式：若复数z 的模为r ，幅角为θ，则有θθθi re i r z =+=)sin (cos ；（8）指数函数是周期i π2为得周期函数；（9）指数函数的几何映射性质：由于指数函数有周期i π2，所以研究当z 在带形}2Im 0C,|{π<<∈=z z z B 中变化时，函数z e w =的映射性质。

第二章 复变函数第一节 解析函数的概念及C.-R.方程1、导数、解析函数定义2.1：设()w f z =是在区域D 内确定的单值函数，并且0z D ∈。

如果极限00,0()()limz z z Df z f z z z →∈--存在，为复数a ，则称)(z f 在0z 处可导或可微，极限a 称为)(z f 在0z 处的导数，记作0'()fz ，或z z dw dz=。

定义2.2：如果()f z 在0z 及0z 的某个邻域内处处可导，则称()f z 在0z 处解析；如果()f z 在区域D 内处处解析，则我们称()f z 在D 内解析，也称()f z 是D 的解析函数。

解析函数的导（函）数一般记为'()f z 或d ()d f z z。

注解1、εδ-语言，如果任给0ε>，可以找到一个与ε有关的正数()0δδε=>，使得当z E ∈，并且0||z z δ-<时，00()()||f z f z a z z ε--<-，则称)(z f 在0z 处可导。

注解2、解析性与连续性：在一个点的可导的函数必然是这个点的连续函数；反之不一定成立；注解3、解析性与可导性：在一个点的可导性是一个局部概念，而解析性是一个整体概念；注解4、函数在一个点解析，是指在这个点的某个邻域内解析，因此在此点可导；反之，在一个点的可导性不能得到在这个点解析。

解析函数的四则运算：()f z 和()g z 在区域D 内解析，那么()()f z g z ±，()()f z g z ，()/()f z g z （分母不为零）也在区域D内解析，并且有下面的导数的四则运算法则：(()())''()'()[()()]''()()()'()f zg z f z g z f z g z f z g z f z g z ±=±=+2()'()()()'()()[()]'f z f z g z f z g z g z g z -⎡⎤=⎣⎦。