应力应变张量分解
- 格式:pdf
- 大小:298.25 KB
- 文档页数:15









我所认识的应力应变关系应力应变都是物体受到外界载荷产生的响应。
物体由于受到外界载荷后,在物体内部各部分之间要产生互相之间的力的作用,由于受到力的作用就会产生相应的变形;或者由于变形引起相应的力的作用。
则一定材料的物体其产生的应力和应变也必然存在一定的关系。
一应力-应变关系影响本构关系的因素有很多,例如材料、环境、加载类型(载荷、温度)、加载速度(动载荷、静载荷)等,当然,本构关系有很多类型,包括弹性、塑性、粘弹性、粘塑性、各向同性、各向异性本构关系,那么首先来叙述一下简单情况本构关系,所谓简单情况就是六个应力分量x y xy yz zx、、z 、、、只有一个不为零,六个应变分量x y xy yz zx、、z 、、、只有一个自由变化,应力应变关系图1-1。
图1-1 应力应变关系图图中OA 为线弹性阶段,AB 为非线弹性阶段,故OB 为初始弹性阶段,C 点位初始屈服点,s为初始屈服应力,CBA 为弹性阶段卸载,这一阶段中E ,初始弹性阶段结束之后,应力继续增大,进入塑性阶段,CDE 为强化阶段,应变强化硬化,EF 为颈缩阶段,应变弱化软化。
如果在进入塑性阶段卸载后再加载,例如在D点卸载至零,应力应变关系自D点沿'DO∥OA,其中DO到达'O点,且''OO为塑性应变p,DG为弹性应变e,总应变为它们之和。
此后再继续加载,为应力应变关系沿ODEF变化,D点为后继屈服点,OD为后继弹性阶段,'s后继屈服应力,值得一提的是初始屈服点只有一个,而后继屈服点有无数个(由加载历史决定)。
若在卸除全部载荷后反向加载,弹性阶段'COC,s s,而在强化阶段',称为Bauschinger效应。
DOD,s s从上述分析得出材料弹塑性行为有一定的特殊性,主要表现在:弹性应力应变关系是线性,且是单值对应关系,而塑性应力应变关系是非线性的非单值对应。
因为通常情况下物体不仅仅处于简单应力状态,那么复杂应力状态下应力应变关系又如何呢?如果我们将材料性质理想化即假设材料是连续的、均匀的、各向同性的,忽略T、t的影响,忽略净水压力对塑性变形的影响,可以将应力应变关系归结为不同的类型,包括理想线弹性模型、理想刚塑性模型、线性强化刚塑性模型、理想弹塑性模型、线性强化弹塑性模型、幂强化模型、等向强化模型、随动强化模型。
不同材料应力应变曲线分解
应力-应变曲线是材料力学性能测试中常见的曲线,它反映了材料在外
界施加载荷时的应变行为。
不同材料的应力-应变曲线形状和特性有一
定的差异,可以根据材料的性质和特点将其分解为不同的部分。
1. 弹性阶段:在应力小于材料的屈服强度时,材料表现出线性弹性行为。
这个阶段应力和应变成正比,称为胡克定律。
材料在这个阶段内
具有良好的恢复性。
2. 屈服阶段:当应力逐渐增大,达到或超过材料的屈服强度(或屈服点),材料会发生塑性变形,应变会出现非线性增加。
在这个阶段内,
材料的应力会逐渐减小,但并不恢复原状。
3. 塑性流动阶段:当应力继续增大,材料会出现塑性流动,此时应力
和应变关系呈非线性增长。
材料的应变会持续增加,而应力不再减小。
4. 极限强度阶段:当应力接近材料的极限强度时,材料会出现明显的
变形和破坏,应变急剧增加。
5. 断裂阶段:当应力超过材料的极限强度时,材料会发生断裂,应变
突然增加并导致材料失效。
需要注意的是,不同材料的应力-应变曲线可能会有所不同,例如金属
材料的应力-应变曲线常常显示出明显的屈服点和流动平台。
而非金属
材料如陶瓷和聚合物等,可能会表现出更加复杂的曲线形状。
材料的
温度、应变速率等因素也会对应力-应变曲线产生影响。
我所认识的应力和应变应力表示内力在截面上某一点的分布集度,它是一个矢量,不仅有大小和方向,而且和点的位置以及通过该点界面方向有关。
应力的国际单位为2/N m ,简写Pa 。
若把应力矢量Pn 沿微分面的线方向和切线方向分解,则沿法线方向的应力分量n σ称为主应力,沿切线方向的应力分量n τ称为剪应力。
应力是二阶张量,由于一点的应力矢量与该点的位置以及通过该点界面的方向有关,所以,凡提到应力,应同时指明它是对物体内的哪一点,并过该点的哪一个微分面。
应力分量的正负号规定为正面正向为正,负面负向为正。
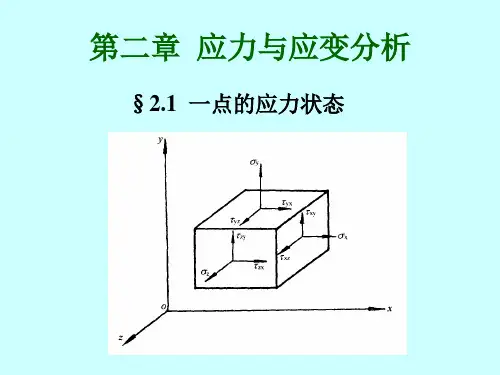
在同一点的三个垂直微分面上共有9个应力张量,这9个应力分量作为一个整体组成所谓的二阶张量,称为应力张量,而其中的每个量,就称为为应力张量的分量。
记应力张量为ij σ并表示为x xy xy ij xy y xy xy xy z σττστστττσ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦,应力张量ij σ描绘了一点处的应力状态,即只要知道了一点的应力张量ij σ,就可以完全确定通过该点的各个微分面上的应力。
主应力:在受力物体内一点任意方向的微分方向上,一般都有正应力和剪应力分量存在。
但是通过某一点的微分面发生旋转时,它的发现方向也会改变,骑上的正应力和剪应力分量的数值也会发生变化,在旋转到某一微分面时只有正应力分量而没有剪应力的微分面称为主平面,其法线方向称为应力方向,,其上的正应力就称为主应力。
主应力空间:在物体内的同一点处,必定存在三个互相垂直的主方向。
若把这三个互相垂直的主方向取为坐标系的三个坐标轴方向,依次建立起来的几何空间,称为主应力空间。
该空间的三个坐标称为应力主轴。
在主应力空间里,该点的应力张量ij σ可以表示为123000000ij σσσσ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦,式中:1σ,2σ和3σ为主应力。
通过同一点的所有微面上的正应力中最大和最小的是主应力;并且通过同一点的任意微分面上的总应力其绝对值介于最大主应力和最小主应力的绝对值之间。