下载文档原格式
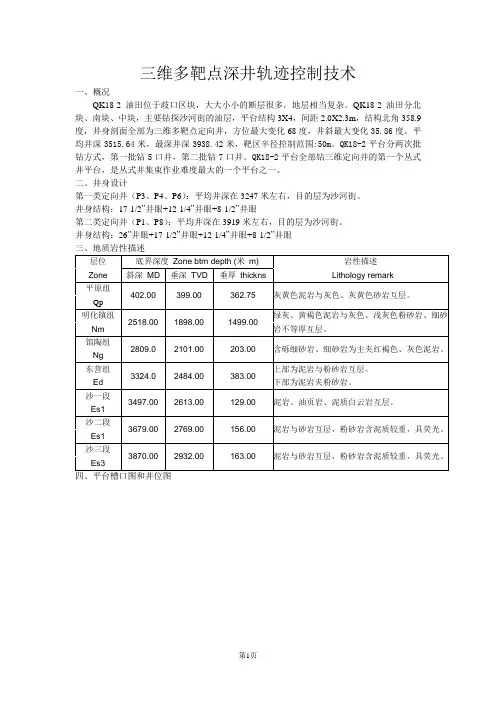
三维多靶点深井轨迹控制技术一、概况QK18-2油田位于歧口区块，大大小小的断层很多，地层相当复杂。
QK18-2油田分北块、南块、中块，主要钻探沙河街的油层，平台结构3X4，间距2.0X2.3m，结构北角358.9度，井身剖面全部为三维多靶点定向井，方位最大变化68度，井斜最大变化35.86度。
平均井深3515.64米，最深井深3938.42米，靶区半径控制范围:50m。
QK18-2平台分两次批钻方式，第一批钻5口井，第二批钻7口井。
QK18-2平台全部钻三维定向井的第一个丛式井平台，是丛式井集束作业难度最大的一个平台之一。
二、井身设计第一类定向井（P3、P4、P6）：平均井深在3247米左右，目的层为沙河街。
井身结构：17-1/2”井眼+12-1/4”井眼+8-1/2”井眼第二类定向井（P1、P8）：平均井深在3919米左右，目的层为沙河街。
井身结构：26”井眼+17-1/2”井眼+12-1/4”井眼+8-1/2”井眼四、平台槽口图和井位图五、项目难点1、深井作业安全问题。
2、克服摩阻，保证滑动钻进。
3、二次造斜，二次造斜点深，是否容易造斜，是否滑得动。
4、合理优化轨迹。
六、施工思路大位移三维多靶点定向井最大的困难是如何克服摩阻，保证滑动钻进和井眼轨迹合理控制。
在井眼轨迹需要调整时，能够及时的调整，如果各方面原因不能调整时，怎样合理的把困难有效的克服，顺利中靶，是我们工作的重点。
1、总结本地区各地层的漂移规律，合理利用地层的自然漂移规律，达到有效控制井眼轨迹的目的。
2、裸眼井段长，摩阻大，扶正器托压严重，不能滑动钻进时，在轨迹控制不失控的情况下，合理利用井身结构，把困难转移到下一个井段或改变钻具组合。
3、合理选择第二造斜点，合理选择造斜率。
4、从始至终，要准确的预测井眼轨迹。
5、合理选择马达弯角，使之能够满足井眼轨迹控制的需要。
6、优化井眼轨迹，降低作业难度。
七、井眼轨迹控制下面以P8井为例介绍井眼轨迹控制技术，中间穿插其它井遇到特殊情况下的轨迹控制：1、26"井眼轨迹控制26"井眼主要任务是防斜打直，做好防碰扫描。
第三章定向井、水平井井身轨迹控制技术第一节定向井、水平井井眼轨迹控制理论无论是定向井，还是水平井，控制井眼轨迹的最终目的都是要按设计要求中靶。
但因水平井的井身剖面特点、目的层靶区的要求等与普通定向井和多目标井不同，在井眼轨迹控制方面具有许多与定向井、多目标井不同的新概念，需要建立一套新的概念和理论体系来作为水平井井眼轨迹控制的理论依据和指导思想。
我们在长、中半径水平井的井眼轨迹控制模式的形成和验证过程中，针对不断出现的轨迹控制问题，建立了适应于水平井轨迹控制特点的几个新概念。
一、水平井的中靶概念地质给出的水平井靶区通常是一个在目的层内以设计的水平井眼轨道为轴线的柱状靶，其横截面多为矩形或圆。
我们可以把这个柱状靶看成是由无数个相互平行的法面平面组成，因此，控制水平井井眼轨迹中靶，与普通定向井、多目标井是个截然不同的新概念，主要体现是:井眼轨迹中靶时进入的平面是一个法平面（也称目标窗口），但中靶的靶区不是一个平面，而是一个柱状体，因此，不仅要求实钻轨迹点在窗口平面的设计范围内，而且要求点的矢量方向符合设计，使实钻轨迹点在进入目标窗口平面后的每一个点都处于靶柱所限制的范围内。
也就是说，控制水平井井眼轨迹中靶的要素是实钻轨迹在靶柱内的每一点的位置要到位（即入靶点的井斜角、方位角、垂深和位移在设计要求的范围内），也就是我们所讲的矢量中靶。
二、水平井增斜井段井眼轨迹控制的特点及影响因素对一口实钻水平井，从造斜点到目的层入靶点的设计垂深增量和水平位移增量是一定的，如果实钻轨迹点的位置和矢量方向偏离设计轨道，势必改变待钻井眼的垂深增量和位移增量的关系，也直接影响到待钻井眼轨迹的中靶精度。
水平井钻井工程设计中所给定的钻具组合是在一定的理论计算和实践经验的基础上得出的，随着理性认识的深化和实践经验总结，设计的钻具组合钻出实际井眼轨迹与设计轨道曲线的符合程度会不断提高。
但是，由于井下条件的复杂性和多变性，这个符合程度总是相对的。
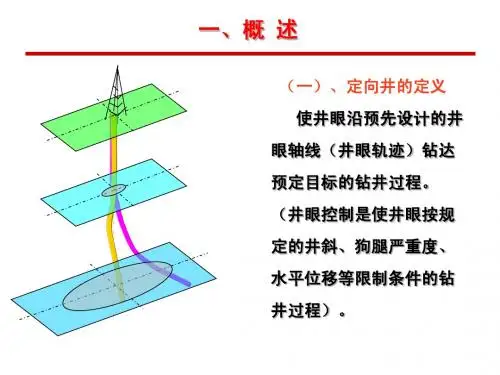
1.井眼轨迹的基本概念1.1定向井的定义定向井是按预先设计的井斜角、方位角及井眼轴线形状进行钻进的井。
（井斜控制是使井眼按规定的井斜、狗腿严重度、水平位移等限制条件的钻井过程）。
1.2井眼轨迹的基本参数所谓井眼轨迹，实指井眼轴线。
测斜：一口实钻井的井眼轴线乃是一条空间曲线。
为了进行轨迹控制，就要了解这条空间曲线的形状，就要进行轨迹测量，这就是“测斜”。
测点与测段：目前常用的测斜方法并不是连续测斜，而是每隔一定长度的井段测一个点。
这些井段被称为“测段”，这些点被称为“测点”。
基本参数：测斜仪器在每个点上测得的参数有三个，即井深、井斜角和井斜方位角。
这三个参数就是轨迹的基本参数。
井深：指井口(通常以转盘面为基准)至测点的井眼长度，也有人称之为斜深，国外称为测量井深(Measure Depth)。
井深是以钻柱或电缆的长度来量测。
井深既是测点的基本参数之一，又是表明测点位置的标志。
井深常以字母Ｌ表示，单位为米(m)。
井深的增量称为井段，以ΔＬ表示。
二测点之间的井段长度称为段长。
一个测段的两个测点中，井深小的称为上测点，井深大的称为下测点。
井深的增量总是下测点井深减去上测点井深。
井斜角：井眼轴线上每一点都有自己的井眼前进方向。
过井眼轴线上的某点作井眼轴线的切线，该切线向井眼前进方向延伸的部分称为井眼方向线。
井眼方向线与重力线之间的夹角就是井斜角。
井斜角常以希腊字母α表示，单位为度(°)。
一个测段内井斜角的增量总是下测点井斜角减去上测点井斜角，以Δα表示。
井斜方位角：井眼轴线上每一点，都有其井眼方位线；称为井眼方位线，或井斜方位线。
井眼轴线上某点处的井眼方向线投影到水平面上，即为该点的井眼方位线（井斜方位线）以正北方位线为始边，顺时针方向旋转到井眼方位线（井斜方位线）上所转过的角度，即井眼方位角。
井斜方位角常以字母θ表示，单位为度(°)。
井斜方位角的增量是下测点的井斜方位角减去上测点的井斜方位角，以Δθ表示。
定向井钻井轨迹设计与控制技术研究摘要：在定向井钻井过程中，井眼轨迹的设计和控制至关重要，它可以决定定向井施工的成败。
因此，有必要进一步探索定向井井眼轨迹的设计和控制技术，以实现安全、优质、高效的定向井施工。
定向井轨迹的选择对钻井施工的安全、高效、低成本起着重要作用。
关键词：定向井；钻井轨迹；设计；轨迹控制前言近年来，随着钻井工程技术和钻井设备的不断改进，钻井技术得到了快速发展。
定向钻井作为一种非常重要和实用的钻井方法，受到了人们的极大关注。
井眼轨迹设计技术是一整套钻井技术中的第一个关键环节。
定向井是指根据预先设计的井斜方向和井筒轴线形状钻探的井。
换句话说，任何设计目标偏离井口所在垂直线的井都属于定向井。
定向井是相对于垂直井而言的，根据设计的井筒轴线分为二维定向井和三维定向井。
由于油气资源短缺以及当前油气生产中遇到的问题，为定向井轨迹设计提供了广阔的发展前景和空间。
定向井轨迹的设计方法和实际钻井偏移测量理论将是研究的重要趋势。
现在，进入计算机快速发展时期，将现有和更成熟的工程模型计算机化，以提高现场施工人员的工作效率；另一方面，准确及时地将现场数据输入计算机，为未来的数据统计和科研分析提供第一手现场真实数据。
因此，利用定向井轨迹设计的软件实现和强大的计算机编程功能，实现了定向井轨迹优化设计软件的研究。
通过不断的实验和改进，设计的轨迹不仅满足了施工现场条件的限制，而且是满足各种设计条件的理想轨迹。
1.定向井轨迹概念井眼轨迹可分为两类：设计轨迹和实际钻井轨迹。
其中，设计轨迹可分为钻孔前设计的轨迹和钻孔过程中钻孔时修改或调整的轨迹。
设计轨迹通常由一些分段的特殊曲线组成，具有很强的规律性。
设计轨迹和实际钻井轨迹都是连续光滑的空间曲线，只有一条线，在三维空间中随机变化，没有任何规则可循。
为了表达这样的曲线，可以使用图形来显示井轨迹的形状，或者使用几何参数来描述井轨迹的形式。
这两种方法相互补充，并且通常以一种既考虑到图形方法的视觉和直观特性，又考虑到精确和灵活的分析参数的优势的方式应用。
ICS 75.020E 13备案号：6829－2000中华人民共和国石油天然气行业标准SY/T 5435－2000定向井轨道设计与轨迹绘图Methods of directional well pathDesigning＆trajectory graphing2000－03－10 发布2000－03－01 实施国家石油和化学工业局发布SY/T 5435－2000目次前言……………………………………………………………………………………………IN1 范围 (1)2 引用标准 (1)3 定义 (1)4 轨道形状、设计原则、设计条件及轨道类型的选择 (2)5 轨道的设计计算 (4)6 实钻井眼轨迹的计算和绘图 (10)附录A（标准的附录）参数的代号 (14)附录B（标准的附录）轨道设计结果的表述 (18)附录C（标准的附录）轨道形状图及轨迹计算图 (19)附录D（提示的附录）轨道设计及轨迹计算举例 (22)中华人民共和国石油天然气行业标准SY/T 5435－2000定向井轨道设计与轨迹绘图代替SY/T 5435－92SY/T 5949－94Methods of directional well pathdesigning＆trajectory graphing1 范围本标准规定了两维和三维绕障定向井轨道类型的选择及设计原则、计算公式、设计结果的表述以及实钻井眼的轨迹计算和绘图。
本标准适用于石油天然气钻井和石油地质勘查的两维和三维绕障定向井轨道设计及轨迹绘图。
2 引用标准下列标准所包含的条文，通过在本标准中引用而构成为本标准的条文。
本标准出版时，所示版本均为有效。
所有标准都会被修订，使用本标准的各方应探讨使用下列标准最新版本的可能性。
SY/T 5088－93 评定井身质量的项目和计算方法3 定义本标准采用下列定义。
1.两维常规定向井 2－dimension normal directional well设计方位角、设计轨道的增斜率和降斜率均为常数的定向井。
第四章 三维多目标定向井轨道设计井眼按照其轴线形状可以分为三类：垂直井、二维定向井和三维定向井。
这个分类并不是根据实钻的井眼形状，而是根据设计的井眼形状来分的。
原设计的两维定向井，实钻出来的井眼形状都是三维的，但它们仍被称为两维定向井。
这好象原来设计为垂直井，而实钻出来的井眼都有一定的井斜角和方位角。
它仍被称为垂直井一样。
只有当设计的井眼轴线，既有井斜角变化，又有方位角的变化，才能称为三维定向井。
三维定向井的设计和施工，都比两维定向井困难，三维设计的思路和方法，是将三维设计转化为两维设计。
本文重点讨论三维双目标及三目标的设计的问题。
第一节 一般三维双目标定向井轨道设计三维双目标定向井的设计，其设计方法与一般普通定向井设计一样，在已知第一靶垂深1H 、第一靶方位1φ、第一靶位移1A ，第二靶方位2φ、第二靶位移2A 、第二靶垂深2H ，造斜点井深a D ，第一靶后增降斜率z K 和变方位曲率K 参数下，进行基本参数计算。
1、基本参数计算1.1 计算两靶位移差和两靶垂深差12A A A -=∆ 12H H H -=∆1.2 计算过渡参数a e D H D -=1 1A S e =z z K R /5730=1.3 计算最大井斜角)2/(2(2221max e z e z e e e S R S R S D D tg -++⋅=-α1.4 各井段参数的计算和结果验算1.4.1 增斜段参数max α⋅+=z a z R D Lmax sin α⋅=z z R D)cos 1(max α-=z z R S1.4.2稳斜段参数e z e e w S R S D L 222-+=max cos α⋅=w w L D max sin α⋅=w w L S 2、扭方位段的设计中第一靶后，后续设计为扭方位设计。
其设计方式有：可设计为稳斜变方位井段后接变井斜（或稳井斜）稳方位井段的设计。
令：2H D t =2A S t = 2φφ=b 11cos φ⋅=A N b 11sin φA E b = 1H D b = max α=b A 1φφ=b wz b L L L +=2.1 设计水平投影图的主要参数 1sin φt t S E =1cos φt t S N =1A S b =扭方位点自b 点至t 点的设计示意图见图1，图2图1 扭方位设计2.2 扭方位轨道设计方法2.2.1设计水平投影图的主要参数计算变方位段水平投影曲率半径a R :πα5400sin 2⋅=K R b a（1） 计算变方位段方位扭转角A(见图3)'-'+-+=t a t t a t t a N R E arctg E R N E R arctg A 222（2）计算水平投影总长度S:)2(18022'⋅-++⋅⋅+=t a t t ab E R N E R A S S π （3）式（2）、（3）中''t t N E ,分别按下列式子计算：b b t b b t t N N E E N φφcos )(sin )(-+-=' （4）b b t b b t t N N E E E φφsin )(cos )(---=' （5）2.2.2垂直剖面图的设计计算变方位段终点与目标点连线井斜角c α：tt D S arctg Lc ∆∆=α （6） 式（6）中t t D S ∆∆,分别按下列式子计算：180πα⋅⋅--=∆b a b t t tg R A D D D （7）5.022)2('-+=∆t a t t t E R N E S （8）图2 扭方位水平投影图2.2.3 变方位段终点与目标点之间井段设计：A ：变方位段终点与目标点之间井段设计为增（降）斜段，计算井斜角变化t α∆增斜段（或降斜段）曲率半径)(n z R R 和轨道长度t L ∆。
b c t ααα-=∆2 （9）)2sin(2)(5.0220t t t S D R α∆∆+∆= （10）παtt R L ∆⋅=∆0180 （11）增斜时00;R R R R n z ==降斜时。
B ：变方位段终点与目标点之间井段设计为增（降）斜段后接稳斜段，计算井斜角变化t t L ∆∆和轨道长度α。
005.000202002)2(2A R A R A H H arctg t -⋅-+-=∆α （12）5.00020200)2(180A R A H R L t t ⋅-++∆⋅⋅=∆απ （13）式（12）、（13）中:,00分别按下列式子计算A Hb c t t D S H αα-⋅∆+∆=cos )(5.0220 （14）b c t t D S A αα-⋅∆+∆=sin )(5.0220 （15）增斜时zz K R R ⋅==π54000；降斜时n n K R R ⋅==π54000 2.2.4井眼轨道参数计算图3 计算变方位段扭转角变方位段轨道上任意点计算方位角的井斜角i i i Φ,α：b i αα= （16）b bib i L K αφφsin 30⋅±= （17）式（17）中当b t φφ>时，取“+”号；当b t φφ<时，取“－”号。
稳方位段属于二维常规定向井设计，其参数可按SY/T5435有关条款计算。
第二节 三维双目标定向井优化设计方法定向井剖面设计方法，已由二维设计发展到三维设计，特别是近年来，计算机技术在定向井的设计与施工中得到了普遍的应用，使得定向井剖面设计的理论与方法更加完善。
常规的二维双目标设计，因不考虑井眼轴线方位的变化，设计方法比较简单，不能指导和解决定向井实际施工中双靶有方位偏差问题，尤其是双靶方位偏差较大、井段较短不足扭方位以及地面井位又受限的情况下，必须寻求一种新的井眼轴线设计方法。
本文提出一种能减少扭方位工作量，在第一靶点达到规定的井斜和方位要求的有条件限制的三维双目标井身轨迹设计方法。
1、设计方法及计算公式有条件要求的三维双目标定向井设计法与常规的二维定向井设计方法和一般的三维绕障设计方法有所区别，其突出特点是在第一靶点达到规定的井斜和方位要求以后，减少中第二靶不必要的扭方位情况，尤其当双目标间距较短不足扭方位时，更体现出此方法的优越性。
设计的重难点在于初始方位的选取。
初始方位选取对于三维双目标定向井设计很重要，其初始方位的选取恰当与否决定了扭方位的工作量。
初始方位区间确定方法，先根据双目标设计条件（111,,φS H ；222,,φS H 两靶的垂深、方位和水平位移），求出两靶连线方位和垂线方位，确定初始方位大致范围，两靶点东西、南北坐标分量)cos(111φ⨯=S N )sin(111φ⨯=S E )cos(222φ⨯=S N )sin(222φ⨯=S E 两靶连线方位：1212E E N N --=φ 垂线方位：)/1(1φφtg tg cx -= 式中：111,,φS H ：第一靶的垂深、闭和方位和水平位移；222,,φS H ：第二靶的垂深、闭和方位和水平位移；11,N E ：第一靶东西、南北分量；22,N E ：第二靶东西、南北分量；初始方位范围就在（1,φφcx ）之间。
设水平投影图内方位变化率a K ，先不考虑井斜变化率，在最后校核时，保证全角变化率在允许范围内即可。
初步选择垂线方位作为初始方位。
其计算顺序为：cx φφβ-=11 φφβ-=12 ||||21ββφ+=∆ 25730sin |sin 21φφβ∆-∆=tg Ka S op式中： φφ,cx ：垂线、两靶连线方位；φ∆：井口到目标点方位变化量。
在保证有造斜段的情况下，以第一靶点规定的井斜、方位（两靶连线方位）垂深、位移为迭代条件，给定一定求解精度，确定出扭方位工作量最小最优初始方位。
2、第一靶点规定井斜角、方位角计算公式在造斜点和造斜率给定条件下，第一靶点规定井斜角计算公式为：a D H H -=10 10S A = z z K R /5730=0020200max 222A R A R A H H arctg z z --+-=α 式中：a D ：造斜点井深；z K ：造斜率/100米；z R ：曲率半径；max α：第一靶规定井斜角。
3、井身各段参数计算（1）造斜段3.57/max α⨯+=z a z R D L maxsin α⨯+=z a z R D D)cos 1(max α-⨯=z z R S（2）稳斜扭方位段a a K R /5730= max sin /3.57/αφ∆⨯+=a z wn R L L max tan /3.57/αφ∆⨯+=a z wn R D D φ∆+=sin a z wn R S Y)cos 1(φ∆-⨯=a wz R X22wn wn wn Y X S +=式中：a R ：扭方位曲率半径。
4、双靶连线井段设计双靶连线井段设计可分两种情况：一是两靶比较近；二是两靶比较远其设计方法有所不同。
对于两靶比较近的情况，较好的办法是采用均匀的增（降）斜率，改变井斜角，使之准确钻达目标点。
在这种情况下，需要设计的参数是：两靶井段的造斜率该有多大；两靶井段井眼长度有多长；钻进这段井眼时井斜角的增量应为多少。
设计已知条件是，钻达第一靶点的规定井斜角，两靶之间的垂增和平增，待求参数计算公式为：max 22αα-∆∆=∆HA arctg dai 2sin 222dai dai A H R α∆∆+∆= 180πα⨯⋅∆=∆dai dai dai R L式中：A ∆：两靶之间的平增；H ∆：两靶之间的垂增；dai α∆：井斜角增量；dai R ：两靶之间的曲率半径；dai L ∆：两靶之间的段长。
在以上公式中，若dai α∆>0，dai R >0则表示两靶井眼之间需要增斜，否则，需要降斜，若0=∆dai α，表示稳斜钻进即可。
两靶连线比较长的情况下，最好不采用单一井段形状，而应先根据给定条件，集中力量改变井斜角，然后稳斜钻达目标点。
设钻达第一靶时的井斜角为max α，两靶连线的平增和垂增为H A ∆∆,，给定增降斜率，可以求得两靶之间的最大井斜角，H A arctg s ∆∆=α若s α<max α，表示两靶之间的井眼需要降斜；若s α>max α，表示两靶之间的井眼需要增斜。
两靶之间的段长为：22A H L ∆+∆=两靶之间井段井斜角的增量为dai α∆，可用下式求得（以增斜为例）：01010*******0101222A R A R A H H arctg dai --+-=∆α 式中：||cos max 01s L H αα-=||sin max 01s L A αα-= 01R 或等于z R ，或重新确定的增斜率。
