新三第20讲 盈亏问题

盈亏问题知识点总结盈亏问题是经济学中的一个重要概念，也是企业管理中的核心问题之一。

盈亏问题主要涉及企业经营状况的评估、决策的制定以及风险的控制等方面。

正确地理解和应对盈亏问题，对企业的经营和发展具有重要意义。

本文将从盈亏问题的概念、原因、影响因素、计算方法、决策依据等方面进行总结，以帮助读者更好地理解和应对盈亏问题。

一、盈亏问题的概念盈亏问题是指企业在经营活动中所获得的利润或亏损的状况。

在商业活动中，盈利是企业赚取的收入超过了成本和费用，而亏损则是成本和费用超过了赚取的收入。

盈亏问题反映了企业的经营状况和绩效表现，对企业的发展战略和经营决策具有重要的指导意义。

二、盈亏问题的原因1. 销售不佳：企业销售不佳是盈亏问题最常见的原因之一。

产品市场需求不足、竞争激烈等因素都可能导致企业销售不佳，从而影响企业的盈利能力。

2. 成本管理不当：企业由于原材料成本、生产成本、管理费用等方面的不当管理，导致盈利能力下降。

3. 经营风险：市场变化、政策调整、自然灾害等外部因素对企业盈亏问题的影响也是不可忽视的。

4. 经营管理不善：企业管理层的决策失误、内部管理不善等内部原因也可能导致企业出现盈亏问题。

5. 资金周转不畅：企业的资金周转不畅也会直接影响企业的盈亏状况，导致企业出现资金链断裂，无法维持正常经营。

三、盈亏问题的影响因素1. 经济环境：宏观经济形势对企业盈亏问题的影响是直接而重要的。

当整体经济增长乏力，市场需求不足时，企业盈利能力必然受到影响。

2. 行业竞争：不同行业的竞争程度不同，竞争激烈的行业，企业要想实现盈利并不容易。

行业竞争的激烈程度直接影响企业在市场上的表现和利润水平。

3. 内部管理：企业的内部管理水平对盈亏问题有着直接的影响。

内部管理水平好的企业，成本控制得当，盈利能力强，反之则难以取得盈利。

4. 资金流动性：企业的资金流动性对盈亏问题同样有着重要的影响。

资金流动性差的企业，很容易陷入盈利难题。

首先，我们需要理解什么是盈亏问题。

盈亏问题是一个关于分组的问题，其中每组的元素数量或数量有一定的差异。

例如，如果你有10个苹果，要分成3组，一组有4个，另一组有3个，还有一组有3个。

这样，前两组和最后一组的苹果数量是不同的，这就是盈亏问题的一种表现。

为了更好地理解盈亏问题，我们可以从以下几个方面进行讲解：1定义：盈亏问题是指一组物品分成若干组时，出现有的组物品多，有的组物品少的情况。

2特点：盈亏问题有两个特点，一是“均分”，二是“不均分”。

例如，将10个苹果分成3组，每组平均分配就是“均分”，而分成4、3、3组则是不均分。

3解决策略：解决盈亏问题需要找到一种方法，使得每组的数量都相等或相差最小。

这可以通过加减运算、代数运算等方法来实现。

4经典问题：盈亏问题有很多经典的例子，比如“分苹果”、“分铅笔”、“分糖果”等问题。

这些问题的解决都需要用到盈亏问题的解决策略。

5应用：盈亏问题在现实生活中也有很多应用，比如在工厂生产中分配原材料、在餐饮业中分配食材等。

解决这些问题需要考虑到资源的合理分配和成本的控制。

对于三年级的学生来说，盈亏问题可能是一个相对抽象的概念，因此需要采用简单易懂的方式进行讲解。

以下是几个通俗易懂的教学案例，可以帮助三年级学生理解盈亏问题:案例一：分苹果假设有10个苹果，要分给3个小朋友，每个小朋友至少分到一个苹果，问怎么分才公平？首先，我们可以让每个小朋友先分到一个苹果，这样还剩下7个苹果。

接下来，我们可以将7个苹果切成3份，每份2个苹果，再加上一个苹果，这样每个小朋友可以得到3 个苹果。

在这个问题中，我们通过盈亏平衡分析的方法，将剩余的苹果分成3份，每份2个，再加上一个苹果，使得每个小朋友都得到了公平的分配。

案例二：分铅笔假设有12支铅笔，要分给4个小朋友，每个小朋友至少分到3支铅笔，问怎么分才公平？首先，我们可以让每个小朋友先分到3支铅笔，这样还剩下6支铅笔。

接下来，我们可以将6支铅笔分成3份，每份2支铅笔，这样每个小朋友可以得到4支铅笔。

六、盈亏问题
按不同的⽅法分配物品时，经常发⽣不能均分的情况．如果有物品剩余就叫盈，如果物品不够就叫亏，这就是盈亏问题的含义．
⼀般地，⼀批物品分给⼀定数量的⼈，第⼀种分配⽅法有多余的物品(盈)，第⼆种分配⽅法则不⾜(亏)，当两种分配⽅法相差n个物品时，那就有：
盈数+亏数= ⼈数×n ，
这是关于盈亏问题很重要的⼀个关系式．
解盈亏问题的窍门可以⽤下⾯的公式来概括：
(盈+亏)÷两次分得之差=⼈数或单位数，
(盈-盈)÷两次分得之差=⼈数或单位数，
(亏 -亏)÷两次分得之差= ⼈数或单位数．
解盈亏问题的关键是要找到：什么情况下会盈，盈多少？什么情况下"亏"，"亏"多少？找到盈亏的根源和⼏次盈亏结果不同的原因．
另外在解题后，应进⾏验算．。

盈亏问题盈是多余的意思。

亏是不足的意思。

在分物品或者安排其他工作时，经常会遇到多余或者不足的情况。

遇到这类题目，我们可以根据多余以及不足的数量找出解题的线索。

这类应用题通常叫做盈亏问题。

解答盈亏问题的关键是弄清盈、亏与两次分配差的关系。

盈亏问题的数量关系是：（1）“一盈一亏”：（盈+亏）*两次分配差二份数“两盈”：（大盈-小盈）十两次分配差=份数“两亏”：（大亏-小亏）十两次分配差=份数（2）每次分的数量X份数+盈=总数量每次分的数量X份数-亏=总数量小朋友分糖果，每人3粒剩2粒，每人5粒少6粒，则共有糖果 ___________ 粒?思路点拨：列出已知条件：每人3粒，多2粒；每人5粒，少6粒。

这属于“一盈一亏”问题。

由题意可知，小朋友的人数和糖果的粒数是不变的。

比较两种分配方案，结果相差2+6=8 （粒），这是因为两种分配方案每人所分糖果相差5-3=2 （粒）所以，小朋友的人数是8宁2=4 （人），再求出糖果一共有多少粒。

例2 羊爷爷买了一些鲜草馒头发给小羊们。

如果给每只小羊发 4个鲜草馒头，还多17 个；如果给每只小羊发6个鲜草馒头，并且给羊爷爷自己也发 3个，还多4个。

那么共有小羊，共买了_________ 鲜草馒头。

思路点拨：列出已知条件：每只小羊发4个，余17个；每只小羊发6个，余（3+4）个。

这是两盈的问题。

由题意可知：小羊的只数和馒头的个数是不变的。

比较两种分配方案，结果相差17- （3+4） =10（个），这是因为两种分配方案每只小羊发到的馒头相差6-4=2 （个）。

所以小羊有10十2=5 （只）。

例3 学校将一批铅笔奖给三好学生。

如果每人奖 9支，则缺45支；如果每人奖7支，则缺7支。

三好学生有多少人？铅笔有多少支？思路点拨：列出已知条件：每人9支，少45支；每人7支，少7支。

这是两亏的问题。

由题意可知：三好学生人数和铅笔支数是不变的。

比较两种分配方案，结果相差45-7=38 （支），这是因为两种分配方案每人得到的铅笔相差 9-7=2 （支），所以三好学生有38 - 2=19 （人）。

盈亏问题解题技巧
1. 嘿，朋友们！来看看这个盈亏问题解题技巧啊。

比如说，你开了个小店卖文具，进了一批笔，每支成本 5 块钱，你想卖 8 块钱来赚点小钱。

要
是这批笔全卖出去了，那就是赚了啊，可要是有很多没卖掉，那不就亏了嘛！这里面的关键就是要找到那个平衡点，能懂不？这就是一个简单的例子让你明白盈亏的概念哟！
2. 哇塞，听好了哈！在解决盈亏问题时，一定要学会比较啊。

就像你玩游戏，要对比自己的得分和别人的得分，才能知道自己是领先还是落后呀。

比如你种了一亩苹果树，预计能收 1000 斤苹果，结果只收了 800 斤，这明显就
是亏了呀，那你就得反思为啥没达到预期，找到问题所在呀，对不对？
3. 嘿呀！还有哦，计算很重要啊！比如说你去炒股，买了一只股票花了 1
万块，后来涨到万卖了，那你不就赚了5000 块嘛。

但要是买了后跌了呢，岂不是就亏啦！所以得仔细计算成本和收益呀，这不是很简单的道理嘛！4. 哎呀呀！一定要看清楚题目要求呀！就像你走路要看清路一样，不然会摔倒的哟。

假如说有个题目说商店搞促销，买一送一，你得知道这里面到底是怎么个盈亏情况呀，别稀里糊涂就搞错了哟！
5. 嘿！别忘了分析细节啊！好比做一道美食，盐放多少，火候多大，都得注意。

例如说一家工厂生产产品，每个环节的成本都要搞清楚，这样才能知道到底是盈还是亏呀，明白不？
6. 哇哦！要灵活运用技巧啊！就像打太极，不能死板。

比如你接了个兼职，工作多少小时给多少钱，那你得算好怎么安排时间最划算，这就是盈亏问题的实际运用呀！总之，学会这些技巧，解决盈亏问题就不在话下啦！我觉得嘛，只要掌握好这些技巧，盈亏问题就一点也不可怕啦！。

三年级数学盈亏问题名师讲解一、盈亏问题的基本概念1. 含义把一定数量的物品平均分给一定数量的人，如果每人少分，则物品有剩余（盈）；如果每人多分，则物品不够（亏）。

已知所盈和所亏的数量，求物品数量和人数的应用题叫盈亏问题。

2. 基本公式（盈+亏）÷两次分配之差 = 人数每次分的数量×人数+盈 = 总数量每次分的数量×人数亏 = 总数量二、例题解析1. 例题1：一盈一亏情况题目：幼儿园小朋友分苹果，如果每人分3个就多11个；如果每人分5个就少5个。

问有多少个小朋友？有多少个苹果？解析：这里是一盈一亏的情况。

盈是11个（多11个苹果），亏是5个（少5个苹果），两次分配之差是5 3=2（个）。

根据公式（盈 + 亏）÷两次分配之差 = 人数，所以小朋友的人数为(11 + 5)÷(5 3)=8（人）。

再根据每次分的数量×人数+盈 = 总数量，苹果的数量为3×8+11 = 35（个）。

2. 例题2：两盈情况题目：老师给优秀学生发奖品，如果每人发5本练习本，则多24本；如果每人发8本练习本，则多3本。

问优秀学生有多少人？练习本有多少本？解析：这是两盈的情况，两次盈数分别是24本和3本，两次分配之差是8 5 = 3（本）。

根据公式（大盈小盈）÷两次分配之差 = 人数，优秀学生人数为(24 3)÷(8 5)=7（人）。

再根据每次分的数量×人数+盈 = 总数量，练习本的数量为5×7+24 = 59（本）。

3. 例题3：两亏情况题目：学校将一批铅笔奖给三好学生。

如果每人奖9支，则缺45支；如果每人奖7支，则缺7支。

三好学生有多少人？铅笔有多少支？解析：这是两亏的情况，两次亏数分别是45支和7支，两次分配之差是9 7 = 2（支）。

根据公式（大亏小亏）÷两次分配之差 = 人数，三好学生人数为(45 7)÷(9 7)=19（人）。

（尖子生培优）专题20盈亏问题三班级数学思维拓展培优讲义（通用版）有的放矢1、人们在安排东西时，假如每份分的数量少一些，会消灭“物品有多余”的状况，这种状况称之为“盈”；反之，假如每份分的数量多一些，以至消灭“物品不足”的状况，那就称为“亏”，依据“一盈”、“一亏”的变化规律，我们可以求出物品的总数或物品所分的份数，这类数学问题一般称它为“盈亏问题”。

2、解“盈亏问题”的基本思想是“比较的思想”。

3、“盈亏问题”的基本公式是：（1）对象数＝（盈＋亏）÷两次安排差（2）总数＝每份个数×对象数＋盈数或总数＝每份个数×对象数－亏数解题的时候，要特殊留意分析题意，弄清哪部分是“盈”，哪部分是“亏”，弄清数量对应变化关系，再列式计算。

此外，还要养成检验的习惯，保证解题正确。

力量巩固提升1．学校支配寝室，假如每间13人就正好住满，假如每间10人，还缺三间寝室，学校有几间寝室？2．新兴机械厂原方案30天生产一批机器，实际每天比原方案多生产80台，结果提前10天完成了任务．这批机器有多少台？3．一盒巧克力，分给15个小伴侣，假如每人1颗，还少2颗，那么这盒巧克力共有几颗？4．幼儿园分糖果，假如每人分4颗，则多出10颗，假如每人分6颗，则缺8颗。

幼儿园有小伴侣多少人？糖果共有多少颗？5．从家到学校，王老师假如每分行100米，就比规定时间迟到5分钟；假如每分行150米，就比规定时间提前5分钟到达．假如王老师要按时到达学校，那么他每分钟应行多少米？6．小胖步行回家，若按常速行走，平均每分钟走50米，由于今日家中有急事，他加快了速度，平均每分钟走60米，结果提前5分钟到家，今日小胖回家走了多少分钟？7．期望学校全体师生乘车去旅游，若每辆车坐36人，则有8人不能上车；若每辆车多坐4人，则恰好多出1辆车，一共有多少辆车？师生一共有多少人？8．一位农夫家里养了白猫、黑猫若干只，假如卖出2只黑猫，白猫和黑猫只数相等；假如卖出1只白猫，黑猫将比白猫多3只．问白猫、黑猫各多少只？9．参与美术活动小组的同学，安排若干支彩色笔，假如每人分4支，那么多12支：假如每人分8支．那么恰有1人没分到笔，问：有多少同学？多少支彩色笔？10．幼儿园王老师买了一些苹果分给小伴侣，若每人分2个，则多20个；若每人分3个，正好分完：若每人分4个，则少20个．聪慧的同学们，你知道幼儿园有多少个小伴侣吗？你知道王老师买了多少个苹果吗？11．一小和二小有同样多的同学参与某项竞赛．学校用汽车把同学运往赛场．一小用的汽车每车坐15人，二小用的汽车每车坐13人，结果是二小比一小多派1辆车．后来每校各增加一人参与竞赛，这样两校需要的汽车就一样多了．最终学校又打算每校增加一人参与竞赛，二小又比一小多派1辆车．问两校共有多少人参与竞赛？12．在一次古诗词竞赛中一共有5道题，答对一题得5分，不答或答错一题扣1分。

盈亏问题应用题解答方法盈亏问题是指在进行商业活动中，通过计算企业或个人的收入与支出的差额，来判断利润的增减情况。

解答盈亏问题时，需要进行一系列的计算和分析，以确定企业或个人的经营状况。

以下是盈亏问题应用题解答的方法：1.确定收入和支出：首先，需要确定的是企业或个人的收入和支出项目。

这些项目通常包括销售额、成本、运营费用、税费等。

收入是指通过商品销售、服务提供等方式所获得的货币或实物价值。

支出是指为了获取收入而支付的成本、费用或税金。

2.计算净利润：净利润是指收入减去支出后的剩余金额。

根据收入和支出的明细，将收入的总和减去支出的总和，即可得到净利润。

净利润的正值表示盈利，负值表示亏损。

3.分析原因：在计算净利润之后，需要分析导致企业或个人盈亏的原因。

通过对不同收入和支出项目的分析，可以确定哪些项目对净利润产生了积极影响，哪些项目对净利润产生了消极影响。

例如，销售额增加、成本降低、费用控制等因素都可能导致盈利增加，而销售额减少、成本增加、费用上升等因素可能导致亏损加剧。

4.制定改善措施：根据盈亏分析结果，可以制定相应的改善措施来提高盈利能力。

例如，通过加大市场推广力度来增加销售额，通过优化生产流程来降低成本，通过精简组织来控制费用等。

改善措施的制定应该与盈亏分析的结果相匹配，重点解决导致亏损的问题，并优化利润增长的潜力。

5.监控和调整：改善措施实施后，需要进行持续的监控和调整。

通过定期检查盈亏状况，对比实际结果与预期结果的差异，及时调整和优化策略。

同时，需要建立有效的财务管理机制，确保账目的准确性和及时性，以便及时发现和纠正潜在的问题。

6.风险控制：除了对盈利能力的改善，还需要注意风险的控制。

盈亏问题的解答中，除了关注净利润的大小，还需要考虑风险的承受能力。

企业或个人应该根据经营特点和风险偏好，制定相应的风险管理策略，通过适当的风险分散和规避措施，来降低财务风险，确保长期的盈利能力。

以上是盈亏问题应用题解答的基本方法。

三年级下春季奥数盈亏问题僧多粥少讲义加练习三年级下春季奥数盈亏问题盈亏问题一直是数学中的重要内容，对于三年级的学生来说，掌握盈亏问题的解题方法和技巧，不仅可以培养他们的逻辑思维能力，也能为将来更深入的数学学习打下基础。

本文将介绍三年级下春季奥数盈亏问题的讲义及练习，帮助学生更好地理解和掌握这一知识点。

一、盈亏问题的概念盈亏问题是指在某种经济交易中，收入与支出之间的差额。

如果收入大于支出，就是盈利；如果支出大于收入，则是亏损。

在解决盈亏问题时，我们通常需要根据给定的条件，使用数学运算方法来计算盈亏的数值。

二、盈亏问题的解题方法1. 利用加法与减法计算在盈亏问题中，常常需要根据给定的条件进行加法与减法运算。

例如，某商店购进一批商品，每件商品的成本为10元，商家希望以20元的价格出售，计算每件商品的盈亏情况就需要用到减法运算：20 - 10 = 10。

通过这种方式，我们可以得到每件商品的盈利数额。

2. 利用乘法与除法计算有些盈亏问题涉及到商品的数量或者比例，此时我们可以利用乘法与除法运算来计算盈亏的数值。

例如，某商店购进一批商品，每件商品的成本为10元，商家希望以20元的价格出售，而商店的成本比例为40%，我们可以通过计算来确定总的盈亏情况：每件商品的盈亏数额为：20 - 10 = 10元，而总的盈亏数额为每件商品盈亏数额乘以商品的数量：10 ×商品的数量。

三、盈亏问题的练习现在，我们来做一些盈亏问题的练习，通过实际的计算来加深对盈亏问题的理解。

1. 问题一：小明去超市购买了一件价格为300元的衣服，他用了一张折扣券，折扣率为20%，那么他实际需要支付的金额是多少？解题思路：首先，我们需要计算折扣的金额，即300 × 20% = 60元。

然后，将原价减去折扣金额，即300 - 60 = 240元。

所以，小明实际需要支付240元。

2. 问题二：某商店购进一批玩具，成本价格为20元，商家希望以30元的价格出售，如果最终销售数量为100件，那么商店的盈亏状况如何？解题思路：首先，我们计算每件商品的盈亏数额，即30 - 20 = 10元。

盈亏问题知识结构盈亏问题的特点是问题中每一同类量都要出现两种不同的情况．分配不足时，称之为“亏”，分配有余称之为“盈”；还有些实际问题，是把一定数量的物品平均分给一定数量的人时，如果每人少分，则物品就有余（也就是盈），如果每人多分，则物品就不足（也就是亏），凡研究这一类算法的应用题叫做“盈亏问题”．可以得出盈亏问题的基本关系式：（盈+亏）+两次分得之差=人数或单位数（盈-盈）+两次分得之差=人数或单位数（亏-亏）+两次分得之差=人数或单位数物品数可由其中一种分法和人数求出.也有的问题两次都有余或两次都不足，不管哪种情况，都是属于按两个数的差求未知数的“盈亏问题”.注意：1.条件转换；2.关系互换.例题精讲【例1】幼儿园的老师给小朋友们发梨。

每人6个就剩12个，每人7个便少11个。

共有位小朋友个梨。

【考点】盈亏问题【难度】1星【题型】填空【关键词】2008年，第6届，走美杯，5年级，决赛【解析】盈亏问题，（11+⑵一（7-6）=23（人），23x6+12=150（个）梨。

【答案】23个小朋友，150个梨。

【巩固】幼儿园老师给几组小朋友分苹果，每组分7个，少3个；每组分6个，则多4个，苹果有个，小朋友共组。

【考点】盈亏问题【难度】1星【题型】填空【关键词】2003年，第1届，希望杯，4年级，1试【解析】盈亏问题中的"盈亏型”，小朋友有（3+4片（7-6）=7组，苹果有7x7-3=46个【答案】46个苹果，7组小朋友。

【例2】学校规定上午8时到校，小明去上学，如果每分种走60米，可提早10分钟到校；如果每分钟走50米，可提早8分钟到校，求小明几时几分离家刚好8时到校？由家到学校的路程是多少？【考点】盈亏问题【难度】2星【题型】解答【解析】小明每分钟走60米，可提早10分钟到校，即到校后还可多走60x10=600（米）；如果每分钟走50米，可提早8分钟到校，即到校后还可多走50x8=400（米），第一种情况比第二种情况每分钟多走60－50=10（米；，就可以多走600－400=200（米；，从而可以求出小明由家到校所需时间．200=（60—50）=20（分钟），所以小明7时40分离家刚好8时到校.由家到校的路程：60x（20—10）=600（米）或：50x（20—8）=600（米）.答案】小明7时40分离家刚好8时到校，学校到家的距离为600米巩固】猫妈妈给小猫分鱼，每只小猫分10条鱼，就多出8条鱼，每只小猫分11条鱼则正好分完，那么一共有多少只小猫？猫妈妈一共有多少条鱼？考点】盈亏问题【难度】2星【题型】解答解析】猫妈妈的第一种方案盈8条鱼，第二种方案不盈不亏，所以盈亏总和是8条，两次分配之差是11-10=1（条），由盈亏问题公式得，有小猫：8一1=8（只），猫妈妈有8x10+8=88（条）鱼.答案】8只小猫，88条鱼例3】用一根长绳测量井的深度，如果绳子两折时，多5米；如果绳子3折时，差4米.求绳子长度和井深.考点】盈亏问题【难度】3星【题型】解答解析】条件转化：两折多5x2=10米三折少4x3=12米井的深度为：（10+12）+（3-2）=22（米）；绳子长度为：（22+5）x2=54（米）答案】绳子长54米，井深22米巩固】用一根长绳测量井的深度，如果绳子3折时，多8米；如果绳子5折时，差2米.求绳子长度和井深.考点】盈亏问题【难度】3星【题型】解答解析】条件转化：三折多8x3=24米五折少2x5=10米井的深度为：（24+10）+（5-3）=17（米）；绳子长度为：（17+8）x3=75（米）答案】绳子长75米，井深17米例4】一家旅店，若每个房间住6人，则16人没有床位；若每个房间住8人，则有一间房间是空出来的.这家旅店有多少个房间？要住宿的人数有多少？【考点】条件转化型盈亏问题【难度】☆☆☆【题型】应用题；解析】这道题在第二个分配方案里并没直接告述我们少多少（即亏是多少），在这种说法中学生可能会错误计算.实际上，在第二种方案中，只要换一个说法：若每个房间住8人，还需要8个人才能住满。

中学数学盈亏问题专题讲解引言数学中的盈亏问题是一类常见的问题，它涉及到收入和支出的计算，是培养学生逻辑思维和解决实际问题能力的重要途径。

本文将针对中学数学盈亏问题展开详细讲解。

盈亏的基本概念盈亏问题通常涉及到两个关键概念：收入和支出。

在数学中，收入可以表示为正数，支出可以表示为负数。

盈利指收入大于支出，亏损指收入小于支出，而平衡指收入等于支出。

盈亏问题的解决方法1. 直接计算法：根据给定的收入和支出，直接相加或相减得到盈亏的结果。

这是最简单直接的方法，适用于较为简单的问题。

2. 代数方程法：将盈亏问题抽象为代数方程，通过解方程得到未知数的值。

这种方法适用于较为复杂的问题，需要将问题转化为代数形式进行求解。

3. 图表法：通过绘制图表展示收入和支出的变化，通过观察图表找出盈亏的规律。

图表法适用于更为复杂的问题，能够直观地展示收入和支出的关系。

实例分析以下将通过几个实例来展示盈亏问题的解决方法。

实例1小明在一次义卖活动中卖出了30个产品，每个产品的售价为20元，他的总支出为200元。

问小明此次活动的盈亏情况如何？解答：首先计算收入：30个产品 * 20元/产品 = 600元。

然后计算盈亏：收入 - 支出 = 600元 - 200元 = 400元。

因此小明此次活动的盈利为400元。

实例2某商店购进了100个商品，每个商品的进价为50元，售价为80元。

求该商店此次购进商品的盈亏情况。

解答：首先计算总支出：100个商品 * 50元/商品 = 5000元。

然后计算总收入：100个商品 * 80元/商品 = 8000元。

最后计算盈亏：总收入 - 总支出 = 8000元 - 5000元 = 3000元。

因此该商店此次购进商品的盈利为3000元。

总结中学数学盈亏问题是培养学生逻辑思维和解决实际问题能力的重要途径。

本文介绍了盈亏的基本概念和解决方法，并通过实例分析展示了如何解决盈亏问题。

希望读者能够通过学习，掌握解决盈亏问题的技巧，提高数学解题能力。

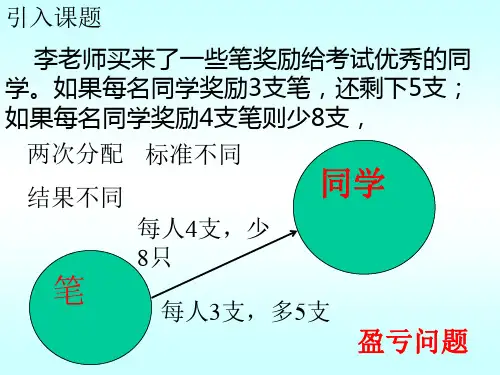
新三第20讲盈亏问题盈亏问题生活中，你是否有过这样的经历?一筐苹果不知有多少个，一群小朋友也不知有多少人。

不允许数小朋友，也不允许数整筐的苹果。

你是否能确切地知道苹果有多少个? 小朋友有多少人?刚开始你可能会感觉茫然，没有头绪，但如果你照下面这样试一试，或许就会有拨开云雾见青天的感觉。

下面是一个同学的尝试：1．如果每人分4个苹果，就剩余39个苹果（盈）；2．如果每人分6个苹果，就剩余15个苹果（盈）；3．如果每人分8个苹果，就不足9个苹果（亏）；4．如果每人分10个苹果，就不足33个苹果（亏）；……看到这里，你或许理解了什么叫盈（多），什么叫亏（少）。

令人称奇的是，只要你从以上不同的分法中任意选取两次分法的结果，比如选取1和2，或2和3，或3和4，……通过比较两次盈（或亏）苹果的相差数量与两次每人分得苹果的相差数量，就可以求出这群小朋友的人数和这筐苹果的个数。

在数学中，把这种因为分配方案的不同，致使分配同一批物体出现有时多（盈）、有时少（亏）的这一类现象称作盈亏问题。

解盈亏问题，关键是求出份数。

求份数分三种情况：1．两次分配中，一次有余（盈），一次不足（亏）；基本公式：（剩余数 + 不足数）÷两次分配之差 = 份数2．两次分配都有余（盈）；基本公式：（剩余数–剩余数）÷两次分配之差 = 份数3．两次分配都不足。

基本公式：（不足数–不足数）÷两次分配之差 = 份数【例1】小羊们割了很多捆青草，它们准备分工将青草运回羊村。

如果每只小羊运3捆，则多出5捆不能运回；如果每只小羊运4捆，则刚好运完。

那么一共有多少捆青草?分析因为小羊只数和青草总捆数都不变，而第二次之所以比第一次多运了5捆，是因为第二次每只小羊比第一次多运了1捆，因此一共有5 ÷（4–3）= 5只小羊。

〖即学即练1〗（1）一根绳子绕树三圈余3尺，如果绕树4圈则正好。

树粗几尺? 绳长几尺?（2）动物园饲养员把一堆桃子分给一群猴子。