可借用氢原子模型→类氢模型氢原子基态电子电离能为

1.电子和空穴的异/同点。

答：不同点：电子带负电，空穴带正电；mp* = -mn*；电子是真实存在的，而空穴是人为假想定义的粒子；电子可以发生共有化运动，发生跃迁，空穴则不能。

相同点：电子和空穴均可以参与导电。

2.什么是回旋共振?答：半导体置于磁感应强度为B的均匀恒定磁场中,半导体中电子受到磁场作用力的方向是垂直于v与B所组成的平面。

从而, 电子在垂直于B的平面内作匀速圆周运动, 运动轨迹是一条螺旋线；再以电磁波通过半导体样品，当交变磁场的角频率ω等于回旋频率ωc时，会发生共振吸收，所以这种情况下，则称产生了回旋共振。

4.浅能级杂质电离能的计算。

答：类氢模型：氢原子中电子的能量为：E n=m0 q4/2（4）2Ч2n2其中n=1,2,3……氢原子基态电子电离能为：E0=E- E1=m0 q4/2（4）2Ч2施主杂质电离能为：受主杂质电离能为：5.杂质补偿作用：在半导体中，同时参杂有施主杂质和受主杂质，而施主杂质和受主杂质之间有相互抵消的作用，通常称为杂质的补偿作用。

6.费米能级的含义。

答:费米能级在半导体物理中是个很重要的物理参数，它是表征量子态是否被电子占据的一个界限，费米能级的位置直观的标志了电子占据量子态的情况。

在热力学零度时，能量比E F小的量子态几乎全部被电子所占据，而能量比E F大的量子态被电子战局的概率几乎为零，所以费米能级标志了电子填充能级的水平。

并且，半导体中，费米能级不是真正的能级，即不一定是允许的单电子能级，所以它可以像束缚状态的能级一样，可以处就等于系统中增加一个电子所引起的系统自由能的变化。

8.影响半导体电导率和迁移率的因素有哪些？答：迁移率的大小与杂质浓度和温度有关，也与外加电场强度有关系。

低掺杂并当室温下杂质全部电离时，杂质浓度越高，电导率越大；重参杂时或当浓度很高时，载流子迁移率随杂质浓度的增加而显著下降。

低温时，杂质散射起主要作用，温度升高，迁移率逐渐增大，电导率上升；当温度达到一定高度时，以晶格振动散射为主，温度继续升高，迁移率下降，电导率下降。

基态电离能计算公式
基态电离能是指在原子或分子的基态（最低能量状态）中，将一个电子从其原子轨道中移出的能量。

电离能通常用电子伏特（eV）或焦耳（J）作为单位。

对于氢原子（H）来说，基态电离能的计算公式可以使用库伦定律和玻尔模型：
E=-(k∙e2/2∙a0)
E是氢原子基态电离能；
k是库伦常数，约为8.9874×109 N∙m2/C2；
e是元电荷，约为1.602×10-19 C；
a0是玻尔半径，约为5.292∙10-11 m；
对于其他原子或分子，基态电离能的计算涉及到更复杂的量子力学模型，通常需要量子力学的方法，例如哈特里-福克方法。

在这些情况下，通常使用专业的计算工具和方法进行求解。

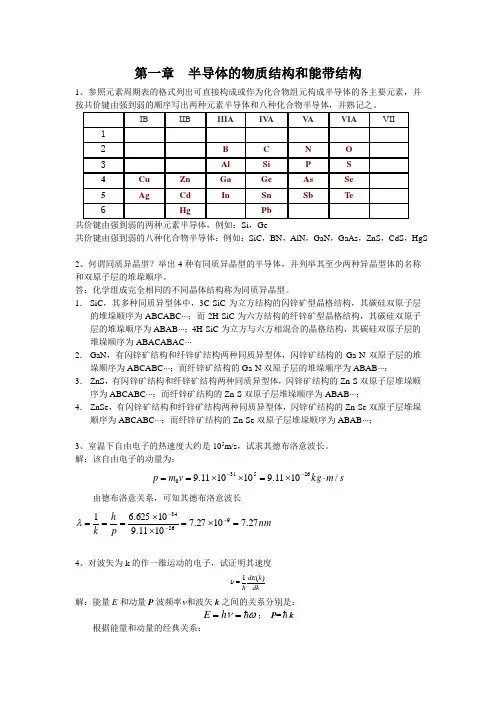
第一章 半导体的物质结构和能带结构1、参照元素周期表的格式列出可直接构成或作为化合物组元构成半导体的各主要元素，并按共价键由强到弱的顺序写出两种元素半导体和八种化合物半导体，并熟记之。

共价键由强到弱的两种元素半导体，例如：Si ，Ge共价键由强到弱的八种化合物半导体：例如：SiC ，BN ，AlN ，GaN ，GaAs ，ZnS ，CdS ，HgS2、何谓同质异晶型？举出4种有同质异晶型的半导体，并列举其至少两种异晶型体的名称和双原子层的堆垛顺序。

答：化学组成完全相同的不同晶体结构称为同质异晶型。

1． SiC ，其多种同质异型体中，3C-SiC 为立方结构的闪锌矿型晶格结构，其碳硅双原子层的堆垛顺序为ABCABC ⋅⋅⋅；而2H-SiC 为六方结构的纤锌矿型晶格结构，其碳硅双原子层的堆垛顺序为ABAB ⋅⋅⋅；4H-SiC 为立方与六方相混合的晶格结构，其碳硅双原子层的堆垛顺序为ABACABAC ⋅⋅⋅2． GaN ，有闪锌矿结构和纤锌矿结构两种同质异型体，闪锌矿结构的Ga-N 双原子层的堆垛顺序为ABCABC ⋅⋅⋅；而纤锌矿结构的Ga-N 双原子层的堆垛顺序为ABAB ⋅⋅⋅；3． ZnS ，有闪锌矿结构和纤锌矿结构两种同质异型体，闪锌矿结构的Zn-S 双原子层堆垛顺序为ABCABC ⋅⋅⋅；而纤锌矿结构的Zn-S 双原子层堆垛顺序为ABAB ⋅⋅⋅；4． ZnSe ，有闪锌矿结构和纤锌矿结构两种同质异型体，闪锌矿结构的Zn-Se 双原子层堆垛顺序为ABCABC ⋅⋅⋅；而纤锌矿结构的Zn-Se 双原子层堆垛顺序为ABAB ⋅⋅⋅；3、室温下自由电子的热速度大约是105m/s ，试求其德布洛意波长。

解：该自由电子的动量为：s m kg v m p /1011.9101011.9265310⋅⨯=⨯⨯==--由德布洛意关系，可知其德布洛意波长nm p h k 27.71027.71011.910625.6192634=⨯=⨯⨯===---λ4、对波矢为k 的作一维运动的电子，试证明其速度dk k dE )(1 =υ解：能量E 和动量P 波频率ν和波矢k 之间的关系分别是：ων ==h E ； P = k根据能量和动量的经典关系：20021,v m E v m P ==由以上两个公式可得：0222m kE =对这个结论求导可得：02)(m kdk k dE η=，进一步得：dk k dE m k )(10ηη= 根据动量的关系：v m k P 0==η可得：=v dkk dE m k)(10ηη=5、对导带底电子，试证明其平均速度和受到外力f 作用时的加速度可分别表示为*/n m k =υ 和 */nm f a = 解：将E （k ）在k=0出按泰勒级数展开取至k 2项，得到....)(21)()0()(20220+++===k dkEd k dk dE E k E k k 因为，k=0时能量取极小值，所以0)(0==k dk dE ，因而2022)(21)0()(k dkEd E k E k ==-令*02221)(1nk m dk E d == 代入上式得*222)0()(nm k E k E =- 根据量子力学概念，波包中心的运动速度为dkd v ω=式中，k 为对应的波矢。

第二章 原子的能级和辐射2.1 试计算氢原子的第一玻尔轨道上电子绕核转动的频率、线速度和加速度。

解：电子在第一玻尔轨道上即年n=1。

根据量子化条件，πφ2h nmvr p ==可得：频率 21211222ma h ma nh a v πππν===赫兹151058.6⨯=速度：61110188.2/2⨯===ma h a v νπ米/秒加速度：222122/10046.9//秒米⨯===a v r v w2.2 试由氢原子的里德伯常数计算基态氢原子的电离电势和第一激发电势。

解：电离能为1E E E i -=∞，把氢原子的能级公式2/n Rhc E n -=代入，得：Rhc hc R E H i =∞-=)111(2=13.60电子伏特。

电离电势：60.13==eE V i i 伏特第一激发能：20.1060.134343)2111(22=⨯==-=Rhc hc R E H i 电子伏特第一激发电势：20.1011==eE V 伏特2.3 用能量为12.5电子伏特的电子去激发基态氢原子，问受激发的氢原子向低能基跃迁时，会出现那些波长的光谱线？解：把氢原子有基态激发到你n=2,3,4……等能级上去所需要的能量是：)111(22n hcRE H-= 其中6.13=HhcR电子伏特2.10)211(6.1321=-⨯=E 电子伏特 1.12)311(6.1322=-⨯=E 电子伏特 8.12)411(6.1323=-⨯=E 电子伏特其中21E E 和小于12.5电子伏特，3E 大于12.5电子伏特。

可见，具有12.5电子伏特能量的电子不足以把基态氢原子激发到4≥n 的能级上去，所以只能出现3≤n 的能级间的跃迁。

跃迁时可能发出的光谱线的波长为：οοολλλλλλAR R AR R AR R HH HH H H 102598)3111(1121543)2111(1656536/5)3121(1322322221221==-===-===-=2.4 试估算一次电离的氦离子+e H 、二次电离的锂离子+iL 的第一玻尔轨道半径、电离电势、第一激发电势和赖曼系第一条谱线波长分别与氢原子的上述物理量之比值。

高中物理氢原子光谱和玻尔的原子模型课后习题答案及解析练习与应用1．什么是线状谱，什么是连续谱？原子的发射光谱是怎样的光谱？不同原子的发射光谱是否有可能相同？解析：线状光谱是原子中电子的两个束缚态能级之间跃迁所产生的发射或吸收光谱，因为能级之间的间隔是确定的并且是离散的，表现出尖锐的光谱线，叫做线状光谱；连续光谱是原子中处于束缚态的电子跃迁到自由散射态或者相反所产生的发射或吸收光谱，因为没有确定的能级间隔，表现出宽泛的，不确定的光谱带，叫做连续光谱；原子的发射光谱是线状光谱。

且不同原子的发射光谱一定不同，这个特点是判断元素种类的依据之一。

2．参考图4.4-6，用玻尔理论解释，当巴耳末公式n＝5 时计算出的氢原子光谱的谱线，是哪两个能级之间的跃迁造成的？解析：巴耳末公式n=5时计算出的氢原子光谱的谱线是量子数为5的能级跃迁到量子数为2的能级形成的。

3．根据巴耳末公式，指出氢原子光谱在可见光范围内波长最长的前两条谱线所对应的n，它们的波长各是多少？氢原子光谱有什么特点？答案：n=3时，λ=6.5×10 -7 m ，n=4时，λ=4.8×10 -7 m ，氢原子光谱是由一系列不连续的谱线组成的.4．如果大量氢原子处在n＝3的能级，会辐射出几种频率的光？其中波长最短的光是在哪两个能级之间跃迁时发出的？解析：3种频率的光，波长最短的光是从n=3的能级跃迁到n=1的能级时发出的光大量原子处在n=3的能级上，能辐射3种频率的光．波长最短的光是从n=3的能级跃迁到n=1的能级时发出的光5．请用玻尔理论解释：为什么原子的发射光谱都是一些分立的亮线？解析：根据玻尔理论，原子从高能级向低能级跃迁时，能量以光子的形式释放出去。

释放的光子能量为跃迁时两能级间能量差，由于原子能级分立而不连续，所以光子能量分立，发射光谱都是一些分立的亮线。

6．要使处于n＝2的激发态的氢原子电离，它需要吸收的能量为多大？氢原子基态能量E1=-13.6eV，由En=E1n2得：E2=E14=-3.4eV，所以要使处于n=2的激发态的氢原子电离，它至少需吸收的能量为3.4eV，吸收的能量等于3.4eV，正好电离，吸收的能量大于3.4eV，氢原子电离，而且还剩余一部分能量以电子的动能形式存在。

第二章 半导体中杂质和缺陷能级 引言 1.实际半导体和理想半导体的区别 理想半导体 实际半导体 原子不是静止在具有严格周期性的晶格的格点上，而在其平衡位置附近振动 原子静止在具有严格周期性的晶格的格点上 半导体不是纯净的，含有若干杂质半导体是纯净的，不含杂质 晶格结构不是完整的，含若干缺陷晶格结构是完整的，不含缺陷 2.杂质的种类根据杂质能级在禁带中的位置将杂质分为两种浅能级杂质：能级接近导电底Ec 或价带顶Ev ；深能级杂质：能级远离导带底Ec 或价带顶Ev ；3.缺陷的种类点缺陷，如空位、间隙原子；线缺陷，如位错；面缺陷，如层错、多晶体中的晶粒间界等§2.1硅、锗晶体中的杂质能级一、杂质与杂质能级杂质：半导体中存在的与本体元素不同的其它元素。

杂质出现在半导体中时，产生的附加势场使严格的周期性势场遭到破坏。

单位体积中的杂质原子数称为杂质浓度。

杂质能级：杂质在禁带中引入的能级。

二、替位式杂质、间隙式杂质杂质原子进入半导体后，有两种方式存在：1.间隙式杂质：杂质原子位于晶格原子间的间隙位置，形成该种杂质时，要求其杂质原子比晶格原子小；2.替位式杂质：杂质原子取代晶格原子而位于晶格点处，形成该种杂质时，要求其原子的大小与被取代的晶格原子的大小比较接近，而且二者的价电子壳层结构也比较接近。

三、施主杂质、施主能级(举例Si 中掺P)如图所示，一个磷原子占据了硅原子的位置。

磷原子有5个价电子，其中4个价电子与周围的4个硅原子形成共价键，还剩余一个价电子。

同时，磷原子所在处也多余一个正电荷+q ，称这个正电荷为正电中心磷离子（P +）。

所以磷原子替代硅原子后，其效果是形成一个正电中心P +和一个多余的价电子。

这个多余的价电子就束缚在正电中心P +的周围。

但是，这种束缚作用比共价键的束缚作用弱得多，只要有很少间隙式杂质替位式杂质硅中的施主杂质的能量就可以使它挣脱束缚，成为导电电子在晶格中自由运动，这是磷原子就成为少了一个价电子的磷离子（P +），它是一个不能移动的正电中心。

类氢杂质和类氢模型半导体施主、受主杂质能级的计算这是在计算半导体中浅能级杂质(Shallowlevelimpurity)的电离能时所经常采用的一种模型，即把束缚着价电子的杂质原子看成为一个类氢原子。

(1)基本概念和能级计算:浅能级杂质就是指在半导体中、其价电子受到束缚较弱的那些杂质原子，往往就是能够提供载流子--电子或空穴的施主、受主杂质;它们在半导体中形成的能级都比较靠近价带顶或导带底，因此称其为浅能级杂质。

例如Si中的施主杂质磷(P)原子，其上多出的一个价电子受到杂质原子中心的束缚较弱，则该电子就很容易被热激发而成为自由的载流子(即进入导带);这就意味着，这种施主杂质的能级离开导带底很近(电离能很小)，是所谓浅能级。

这种受到束缚较弱的电子在晶体中的轨道半径较大[可遍及许多个元胞]，类似氢原子上的束缚电子，因而这些杂质能级的位置可以采用氢原子电离能的计算公式来进行估算，这就是所谓类氢模型。

这种施主或者受主杂质就称为类氢杂质，有时也称为浅能级杂质。

因为氢原子中电子的量子化能量为En=-moq4/(8εo2h2n2),则氢原子基态电子的电离能为ΔEo=E∞-E1=moq4/(8εo2h2)=13.6eV.对于半导体中的施主或者受主杂质原子，它对其价电子的束缚比较弱，则可以采用类氢模型来近似计算它们的电离能，但是这里的电子态又与氢原子的有两点不同:a)电子处于半导体中，若半导体的介电常数为ε=εoεr，则电子受到正电中心的引力将减弱εr倍，束缚能量也将相应地减小εr2倍;b)电子在晶格周期性势场中运动,则电子的质量需用有效质量mn*来代替mo。

因此，对于施主杂质，得到电离能为ΔEd=(mn*/mo)(ΔEo/εr2);对于受主杂质，电离能则为ΔEa=(mp*/mo)(ΔEo/εr2).可见，浅能级杂质的电离能与晶体的有效质量成正比、与介电常数成反比。

对于G e:εr=16，ΔEd=0.05(mn*/mo);因一般(mn*/mo)1，则ΔEd0.05eV;若取1/mn*=(1/ml+2/mt)/3，ml=1.64mo，mt=0.0819m0，则mn*=0.12m0，得到ΔEd=0.0064eV，这与实验在数量级上基本相符。

氢原子基态电离能
氢原子基态电离能的数值为13.6电子伏特，这意味着如果我们想将一个氢原子基态中的电子完全从原子核束缚状态中释放出来，需要提供至少13.6电子伏特的能量。

这个电离能值的大小不仅对于氢原子的性质和结构有着非常重要的作用，同时也对于化学和物理学领域中的许多现象和实验具有重要的参考价值。

例如，在氢原子中，一个电子在基态中的束缚能就与它的第一电离能相等。

这也是为什么氢原子最稳定的状态就是处于基态的原因之一。

此外，氢原子基态电离能还有许多其他的应用。

例如，在分析化学中，我们可以使用这个数值来确定样品中氢原子的含量；在天文学中，我们可以利用这个数值来研究恒星的结构和演化等问题。

- 1 -。