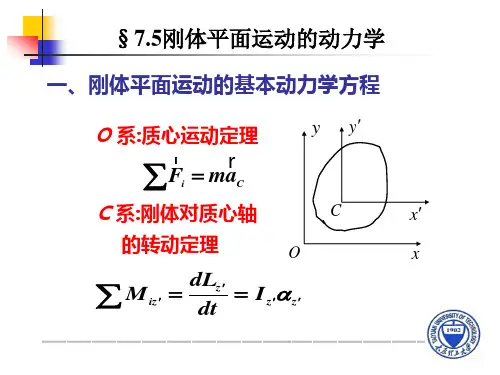
刚体动力学解法例题解
- 格式:pdf
- 大小:824.89 KB
- 文档页数:37

刚体动力学瞬时零点例题一、刚体动力学的瞬时零点是什么?说到刚体动力学,咱们得从头开始聊。
大伙儿可能有些听不懂或者有些模糊,别急,咱慢慢来。
刚体呢,顾名思义,就是不容易变形的物体。
举个例子,想象一块铁板,它无论怎么用力扭,形状都不容易变。
你可以把它看成是“铁板一块”,可刚体的世界里,什么都可能发生。
瞬时零点这个东西,听起来有点深奥对吧?其实它说的就是——物体的某一点在某一瞬间的速度为零。
你瞧,话说得简单,但理解起来,可能有点像把鸡蛋从锅里捞出来还不摔碎。
比如说,一个飞盘飞起来了,它的速度非常快。
但飞盘的中心点呢,可能就在某一时刻,速度会突然变成零。
像是你投球的时候,球刚好在空中停了一下,不动了,就有点那意思。
那停下的地方,就是瞬时零点!简而言之,瞬时零点就是物体在瞬间不动的点。
二、瞬时零点的实际例子咱们生活中,其实有很多瞬时零点的例子。
比如说,摩天轮上最顶端的位置,你坐上去,车厢不动的那一刹那,那时摩天轮的速度为零,就是瞬时零点。
再比如说,抛一个球,球的上升过程中,它有一个最高点,那一瞬间球的速度也是零。
就像你飞翔在空中,猛的一停住,完全没有动静,这就是瞬时零点的存在!好,咱继续聊。
刚才讲的例子,都是想让大家更形象的理解这个瞬时零点。
咱不妨想象一下,一辆汽车在公路上飞驰,忽然你踩刹车停下来。
车轮转速变慢,直到停下,但实际上车的某一个部位,比如车的某一个小点,瞬间就不动了,那就是瞬时零点。
你看,很多事情都发生在你完全没注意到的瞬间,所有的速度,都是在一个“瞬间”里发生的。
这种感觉是不是挺神奇的?三、如何求瞬时零点?好,既然讲到了这些例子,咱们就得提一下,怎么计算瞬时零点呢?这就进入了刚体动力学的难点了。
其实啊,计算瞬时零点并不复杂,最常见的方法就是通过方程来推导。
比如你知道了物体的运动方程,通过求导,你就能找到物体的速度公式。
然后,找到速度为零的那个瞬间,就能得出瞬时零点的位置了。
简单来说,就是你先得弄清楚物体的位置,速度等关系,然后通过数学公式“逆推”出速度为零的时刻和点。



1大学物理-刚体力学习题解答一、选择题1、 B,r v⨯=ω 2、 C, 3 、B, 4 、C, 5、 B, 平轴的力矩和为零,θθsin 2cos lmgNl =,所以2)tan (θmg N =。
6 、B, 7、 A, 32202mgR rdr R mrgrgdm M Rf μππμμ===⎰⎰ 8、 B ,在碰撞过程中,小球和摆对O 轴的角动量守恒,所以有1011sin 100mlv l v m=θ,220v v = 二、填空题1.t 108-==θω ,10-==θβ ,所以s rad s t 62.0==ω;22.010s rad s t -==β; s m R v m R s t 35.0,2.0====ω;()25.0,2.05s m R a m R s t -====βτ;()225.0,2.018s m R a m R s t n ====ω 2s m 18-⋅。
2.刚体对转轴转动惯性大小的量度;2I r dm =⎰;质量、质量分布、转轴的位置。
3.mLv 。
4.()()k t mgv j gt v i v j gt t v i t v v r L αααααcos 21sin cos 21sin cos 200020000-=-+⨯⎪⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛-+=⨯=;k t mgv dt L d αcos 00-=;k t mgv dtL d Mαcos 00-==。
5.角动量;04ω 。
6.同时到达。
7.32g。
8.20012I ω。
三、计算题,1、设1m 向下运动,2m 向上运动,对两物体应用牛顿定律列方程有:1111m g T m a -=,2222T m g m a -=,对鼓轮应用转动定律有:11220T r T r -= ,(因为鼓轮的质量忽略不计) 设鼓轮的角加速度为β,则有:11a r β= ,22a r β= 。
联立求解以上各式得:21122221122m r m r g m r m r β-=+ ;若1m 向上运动,2m 向下运动,则 2211221122m r m r g m r m r β-=+ 。

第3章 刚体力学习题解答 时间2021.03.10 创作:欧阳治3.13 某发动机飞轮在时间间隔t 内的角位移为 ):,:(43s t rad ct bt at θθ-+=。
求t 时刻的角速度和角加速度。
解:23212643ct bt ct bt a dt d dt d-==-+==ωθβω3.14桑塔纳汽车时速为166km/h ,车轮滚动半径为0.26m ,发动机转速与驱动轮转速比为0.909, 问发动机转速为每分多少转?解:设车轮半径为R=0.26m ,发动机转速为n 1, 驱动轮转速为n 2, 汽车速度为v=166km/h 。
显然,汽车前进的速度就是驱动轮边缘的线速度,909.0/2212Rn Rn v ππ==,所以:3.15 如题3-15图所示,质量为m 的空心圆柱体,质量均匀分布,其内外半径为r 1和r 2,求对通过其中心轴的转动惯量。
解:设圆柱体长为h ,则半径为r ,厚为dr 的薄圆筒的质量dm 为:对其轴线的转动惯量dI z 为3.17 如题3-17图所示,一半圆形细杆,半径为,质量为 ,求对过细杆二端 轴的转动惯量。
解:如图所示,圆形细杆对过O 轴且垂直于圆形细杆所在平面的轴的转动惯量为mR 2,根据垂直轴定理z x y I I I =+和问题的对称性知:圆形细杆对过轴的转动惯量为12mR 2,由转动惯量的可加性可求得:半圆形细杆对过细杆二端 轴的转动惯量为:214AA I mR '=3.18 在质量为M ,半径为R 的匀质圆盘上挖出半径为r 的两个圆孔,圆孔中心在半径R 的中点,求剩余部分对过大圆盘中心且与盘面垂直的轴线的转动惯量。
解:大圆盘对过圆盘中心o 且与盘面垂直的轴线(以下简称o 轴)的转动惯量为221MR I =.由于对称放置,两个小圆盘对o 轴的转动惯量相等,设为I’,圆盘质量的面密度σ=M/πR 2,根据平行轴定理,设挖去两个小圆盘后,剩余部分对o 轴的转动惯量为I”3.19一转动系统的转动惯量为I=8.0kgm 2,转速为ω=41.9rad/s,两制动闸瓦对轮的压力都为392N ,闸瓦与轮缘间的摩擦系数为μ=0.4,轮半径为r=0.4m ,问从开始制动到静止需多长时间?解:由转动定理:制动过程可视为匀减速转动,/t αω=∆∆3.20一轻绳绕于r=0.2m 的飞轮边缘,以恒力 F=98N 拉绳,如题3-20图(a )所示。