苏教版高中数学高二选修1-1练习平均变化率

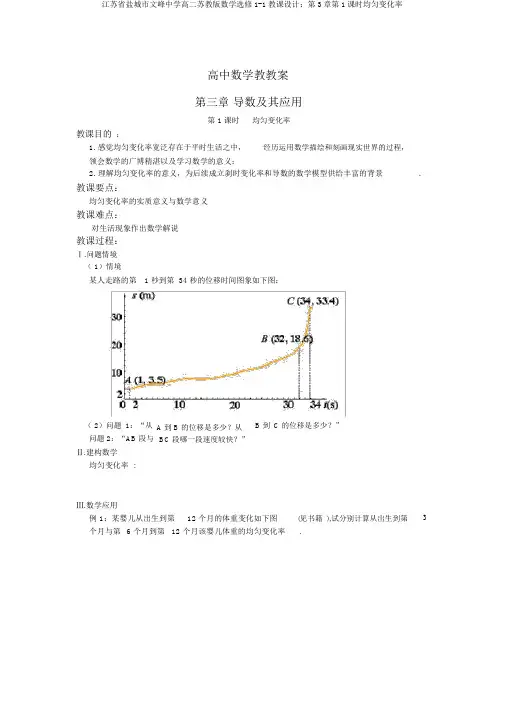
高中数学教教案第三章导数及其应用第 1课时均匀变化率教课目的：1. 感觉均匀变化率宽泛存在于平时生活之中，经历运用数学描绘和刻画现实世界的过程，领会数学的广博精湛以及学习数学的意义；2. 理解均匀变化率的意义，为后续成立刹时变化率和导数的数学模型供给丰富的背景.教课要点：均匀变化率的实质意义与数学意义教课难点：对生活现象作出数学解说教课过程：Ⅰ.问题情境（ 1）情境某人走路的第 1 秒到第 34 秒的位移时间图象如下图：（ 2）问题 1：“从问题 2：“AB 段与Ⅱ.建构数学均匀变化率 :A 到 B 的位移是多少？从BC 段哪一段速度较快？”B 到C 的位移是多少？”Ⅲ.数学应用例 1：某婴儿从出生到第12 个月的体重变化如下图个月与第 6 个月到第12 个月该婴儿体重的均匀变化率(见书籍.),试分别计算从出生到第3变式练习：水经过虹吸管冷静器甲中流向容器乙, t s 后容器甲中水的体积V t5e 0.1t (单位cm3),计算第一个 10s 内 V 的均匀变化率 .例 2：已知函数f x x 2,分别计算 f x 在以下区间上的均匀变化率:(1)1,3(2)1,2(3) 1,1.1(4)1,1.001变式练习：已知函数 f x 2x 1 , g x2x ,分别计算在区间3, 1, 0,5上f x 及 g x 的均匀变化率.Ⅳ.课时小结 :Ⅴ.讲堂检测Ⅵ.课后作业书籍 P59习题 2， 3，41.甲、乙两人投入同样的资本经营某商品，甲用 5 年时间挣到10 万元，已用 5 个月时间挣到 2 万元，怎样比较和评论甲、乙两人的经营成就？2. 已知函数f x x2x ,分别计算 f x 在以下区间上的均匀变化率:(1)1,3(2)1,2(3) 1,1.1(4)1,1.001。

江苏省镇江市丹徒镇高中数学3.1.1 平均变化率学案（无答案）苏教版选修1-1编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（江苏省镇江市丹徒镇高中数学3.1.1 平均变化率学案（无答案）苏教版选修1-1）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为江苏省镇江市丹徒镇高中数学3.1.1 平均变化率学案（无答案）苏教版选修1-1的全部内容。

平均变化率●三维目标1．知识与技能通过丰富的实例，让学生经历平均变化率概念的形成过程，体会平均变化率是刻画变量变化快慢程度的一种数学模型．2．过程与方法理解平均变化率的概念，了解平均变化率的几何意义，会计算函数在某个区间上的平均变化率．3．情感、态度与价值观感受数学模型刻画客观世界的作用，进一步领会变量数学的思想，提高分析问题、解决问题的能力．●重点难点重点：平均变化率的概念．难点：平均变化率概念的形成过程．【问题导思】1．物体从某一时刻开始运动，设s表示此物体经过时间t走过的路程，显然s是时间t 的函数，表示为s＝s（t)．在运动的过程中测得了一些数据,如下表．t/s025101315…s/m069203244…物体在0~2 s和10~13 s这两段时间内,哪一段时间运动得快？如何刻画物体运动的快慢？2．某病人吃完退烧药，他的体温变化如图所示．比较时间x从0 min到20 min和从20 min到30 min体温的变化情况，哪段时间体温变化较快？如何刻画体温变化的快慢?一般地，函数f（x)在区间[x1,x2］上的平均变化率为。

【题型分类】【类型一】平均变化率的概念及意义的应用例1、在经营某商品中，甲挣到10万元，乙挣到2万元，如何比较和评价甲，乙两人的经营成果？变式：在经营某商品中，甲用5年时间挣到10万元，乙用5个月时间挣到2万元，如何比较和评价甲，乙两人的经营成果？例2、水经过虹吸管从容器甲中流向容器乙，t s后容器甲中水的体积0.1=⨯（单位：3()52tV t-cm)，计算第一个10s内V的平均变化率。

2019-2020年高二数学选修1-1平均变化率教案苏教版教学目标：（一）知识目标1．感受平均变化率广泛存在于日常生活之中，经历运用数学描述和刻画现实世界的过程，体会数学的博大精深以及学习数学的意义。

2．理解平均变化率的意义，为后续建立瞬时变化率和导数的数学模型提供丰富的背景。

（二）能力目标体会平均变化率的思想及内涵（三）情感态度与价值观使学生拥有豁达的科学态度，互相合作的风格，勇于探究，积极思考的学习精神教学重点：平均变化率的实际意义与数学意义教学难点：对生活现象作出数学解释教学过程：一．问题情境（1）情境某人走路的第1秒到第34秒的位移时间图象如图所示：（2）问题1：“从A到B的位移是多少？从B到C的位移是多少？”问题2：“AB段与BC段哪一段速度较快？”二．师生活动（1）速度快慢是生活用语，怎样将它数学化？（2）曲线上BC之间一段几乎成了直线，由此联想到如何量化直线的倾斜程度？（3）由点B上升到C点必须考察的大小，但仅注意到的大小能否精确量化BC段陡峭的程度？为什么？（4）在考察的同时必须考察，函数的本质在于一个量的改变本身就隐含着这种改变必定相对于另一个量的改变而言。

三．建构数学（1）通过比较位移在区间上的平均变化率与位移在区间上的平均变化率，感知曲线陡峭程度的量化。

（2）一般地，给出函数在区间上的平均变化率（3）回到位移曲线图中，从数和形两方面对平均变化率进行意义建构（4）用平均变化率来量化一段曲线的陡峭程度是“粗糙不精确的”，但应注意当很小时，这种量化便由“粗糙”逼迫“精确”。

四．课堂练习学生讨论P57练习1，发表见解。

教师补例：甲、乙两汽车，速度从分别加速到和，如何评判两车的性能？五．数学应用例1．P56页例1、例2，并注意小结（1）如何解释例1中从出生到第3个月，婴儿体重平均变化率为1（月）？（2）例1中两个不同的平均变化率的实际意义是什么？（3）例2中是一个随时间变化而变化的量，（）是否表示10秒内每一时刻容器甲中水的体积减少的速度？例2．P57页例3、例4，并注意小结（1）例3、例4均为数学内部的例子，是例1、例2的深化（2）例3中四个区间的变化导致平均变化率有怎样的变化？这种变化的实际意义和数学意义分别是什么？（3）例4讲完后应让学生当堂回答课本中的思考。

2019-2020学年度最新苏教版高中数学苏教版选修1-1学案：3-1-1 平均变化率．1.1平均变化率学习目标 1.通过实例，了解平均变化率的概念，并会求具体函数的平均变化率(重点).2.了解平均变化率概念的形成过程，会在具体的环境中，说明平均变化率的实际意义(难点).3.了解平均变化率的正负(易混点)．知识点一函数的平均变化率在吹气球时，气球的半径r(单位：dm)与气球空气容量(体积)V(单位：L)之间的函数关系是r(V)＝33V4π.思考1当空气容量V从0增加到1 L时，气球的平均膨胀率是多少？思考2当空气容量从V1增加到V2时，气球的平均膨胀率是多少？梳理一般地，函数y＝f(x)在区间[x1，x2]上的平均变化率为________________，其中________________是函数值的改变量．知识点二平均变化率的意义思考如何用数学反映曲线的“陡峭”程度？梳理 平均变化率的几何意义：设A (x 1，f (x 1))，B (x 2，f (x 2))是曲线y ＝f (x )上任意不同的两点，函数y ＝f (x )的平均变化率ΔyΔx＝________________为割线AB 的斜率．类型一 求函数的平均变化率 例1 (1)已知函数f (x )＝2x 2＋3x －5.①求：当x 1＝4，x 2＝5时，函数增量Δy 和平均变化率Δy Δx ； ②求：当x 1＝4，x 2＝4.1时，函数增量Δy 和平均变化率Δy Δx. (2)求函数y ＝f (x )＝x 2在x ＝1,2,3附近的平均变化率，取Δx 都为13，哪一点附近的平均变化率最大？反思与感悟 求平均变化率的主要步骤 (1)先计算函数值的改变量Δy ＝f (x 2)－f (x 1)； (2)再计算自变量的改变量Δx ＝x 2－x 1； (3)得平均变化率Δy Δx ＝f (x 2)－f (x 1)x 2－x 1.跟踪训练1 (1)已知函数f (x )＝x 2＋2x －5的图象上的一点A (－1，－6)及邻近一点B (－1＋Δx ，－6＋Δy )，则ΔyΔx＝________.(2)如图所示是函数y ＝f (x )的图象，则函数f (x )在区间[－1,1]上的平均变化率为________；函数f (x )在区间[0,2]上的平均变化率为________．类型二平均变化率的应用例2在高台跳水运动中，运动员相对于水面的高度h(单位：m)与起跳后的时间t(单位：s)存在函数关系h(t)＝－4.9t2＋6.5t＋10.(1)求运动员在第一个0.5 s内高度h的平均变化率；(2)求高度h在1≤t≤2这段时间内的平均变化率．反思与感悟(1)结合物理知识可知，在第一个0.5 s内高度h的平均变化率为正值，表示此时运动员在起跳后处于上升过程；在1≤t≤2这段时间内，高度h的平均变化率为负值，表示此时运动员已开始向水面下降．事实上平均变化率的值可正、可负也可以是0.(2)平均变化率的应用主要有：求某一时间段内的平均速度，物体受热膨胀率，高度(重量)的平均变化率等等．解决这些问题的关键在于找准自变量和因变量．跟踪训练22012年冬至2013年春，我国北部某省冬麦区遭受严重干旱，根据某市农业部门统计，该市小麦受旱面积如图所示，据图回答：(1)2012年11月至2012年12月间，小麦受旱面积变化大吗？(2)哪个时间段内，小麦受旱面积增幅最大？(3)从2012年11月至2013年2月间，与从2013年1月至2013年2月间，试比较哪个时间段内，小麦受旱面积增幅较大？1．若函数f(x)＝x2的图象上存在点P(1,1)及邻近的点Q(1＋Δx,1＋Δy)，则ΔyΔx的值为________．2．圆的半径r从0.1变化到0.3时，圆的面积S的平均变化率为________．3．如图，函数y＝f(x)在A，B两点间的平均变化率是________．4．如图，函数y＝f(x)在[x1，x2]，[x2，x3]，[x3，x4]这几个区间内，平均变化率最大的一个区间是________．5．甲企业用2年时间获利100万元，乙企业投产6个月时间就获利30万元，如何比较和评价甲、乙两企业的生产效益？(设两企业投产前的投资成本都是10万元)1．准确理解平均变化率的意义是求解平均变化率的关键，其实质是函数值增量Δy与自变量取值增量Δx的比值．涉及具体问题，计算Δy很容易出现运算错误，因此，计算时要注意括号的应用，先列式再化简，这是减少错误的有效方法．2．函数的平均变化率在生产生活中有广泛的应用，如平均速度、平均劳动生产率、面积体积变化率等．解决这类问题的关键是能从实际问题中引出数学模型并列出函数关系式，需注意是相对什么量变化的．提醒：完成作业第3章§3.1 3.1.1答案精析问题导学 知识点一思考1 平均膨胀率为r (1)－r (0)1－0≈0.621＝0.62 (dm/L)．思考2 平均膨胀率为r (V 2)－r (V 1)V 2－V 1.梳理f (x 2)－f (x 1)x 2－x 1Δy ＝f (x 2)－f (x 1) 知识点二思考 如图，表示A 、B 之间的曲线和B 、C 之间的曲线的陡峭程度，可以近似地用直线的斜率来量化．如用比值y C －y Bx C －x B 近似量化B 、C 这一段曲线的陡峭程度，并称该比值是曲线在[x B ，x C ]上的平均变化率． 梳理f (x 2)－f (x 1)x 2－x 1＝f (x 1＋Δx )－f (x 1)Δx题型探究例1 解 (1)因为f (x )＝2x 2＋3x －5， 所以Δy ＝f (x 1＋Δx )－f (x 1)＝2(x 1＋Δx )2＋3(x 1＋Δx )－5－(2x 21＋3x 1－5) ＝2[(Δx )2＋2x 1Δx ]＋3Δx ＝2(Δx )2＋(4x 1＋3)Δx .Δy Δx ＝2(Δx )2＋(4x 1＋3)Δx Δx＝2Δx ＋4x 1＋3.①当x 1＝4，x 2＝5时，Δx ＝1，Δy ＝2(Δx )2＋(4x 1＋3)Δx ＝2＋19＝21， ΔyΔx＝21. ②当x 1＝4，x 2＝4.1时，Δx ＝0.1， Δy ＝2(Δx )2＋(4x 1＋3)Δx ＝0.02＋1.9＝1.92. ΔyΔx＝2Δx ＋4x 1＋3＝19.2. (2)在x ＝1附近的平均变化率为 k 1＝f (1＋Δx )－f (1)Δx ＝(1＋Δx )2－1Δx＝2＋Δx ；在x ＝2附近的平均变化率为 k 2＝f (2＋Δx )－f (2)Δx ＝(2＋Δx )2－22Δx＝4＋Δx ；在x ＝3附近的平均变化率为 k 3＝f (3＋Δx )－f (3)Δx ＝(3＋Δx )2－32Δx＝6＋Δx .当Δx ＝13时，k 1＝2＋13＝73，k 2＝4＋13＝133，k 3＝6＋13＝193.由于k 1<k 2<k 3，所以在x ＝3附近的平均变化率最大． 跟踪训练1 (1)Δx (2)12 34例2 解 (1)运动员在第一个0.5 s 内高度h 的平均变化率为h (0.5)－h (0)0.5－0＝4.05 m/s.(2)在1≤t ≤2这段时间内，高度h 的平均变化率为h (2)－h (1)2－1＝－8.2 m/s.跟踪训练2 解 (1)在2012年11月至2012年12月间，Δs 变化不大，即小麦受旱面积变化不大．(2)由图可知，在2013年1月至2013年2月间，平均变化率ΔsΔt 较大，故小麦受旱面积增幅最大．(3)在2012年11月至2013年2月间，平均变化率＝s B －s A3，在2013年1月至2013年2月间，平均变化率＝s B －s C 1＝s B －s C ，显然k BC >k AB ，即s B －s C >s B －s A3，所以在2013年1月至2013年2月间，小麦受旱面积增幅较大．当堂训练1．2＋Δx 2.0.4π 3.－1 4.[x 3，x 4]5．解 甲企业生产效益的平均变化率为100－1012×2－0＝154.乙企业生产效益的平均变化率为30－106－0＝103.∵154>103， ∴甲企业的生产效益较好．。