准静态电磁场

第四章 准静态电磁场4．1 准静态电磁场1．电准静态场由麦克斯韦方程组知，时变电场由时变电荷和时变磁场产生的感应电压产生。

时变电荷产生库仑电场，时变磁场产生感应电场。

在低频情况下，一般时变磁场产生的感应电场远小于时变电荷产生的库仑电场，可以忽略。

此时，时变电场满足ρ=∙∇≈⨯∇D 0E 称为电准静态场。

可见，电准静态场与静电场类似，可以定义时变电位函数ϕ ，即ϕ-∇=E且满足泊松方程ερϕ-=∇2 与电准静态场对应的时变磁场满足 0t =∙∇∂∂+=⨯∇B DE H γ 2．磁准静态场由麦克斯韦方程组知，时变磁场由时变传导电流和时变电场产生的位移电流产生。

在低频情况下，一般位移电流密度远小于时变传导电流密度，可以忽略。

此时，时变磁场满足0=∙∇≈⨯∇B J H c称为磁准静态场。

可见，磁准静态场与恒定磁场类似，可以定义时变矢量位函数A ，即A B ⨯∇=且满足矢量泊松方程c J A μ-=∇2与磁准静态场对应的时变电场满足ρ=∙∇∂∂-=⨯∇D B E t例1：图示圆形平板电容器，极板间距d = 0.5 cm ，电容器填充εr =5.4的云母介质。

忽略边缘效应，极板间外施电压t t u 314cos 2110)(=V ，求极板间的电场与磁场。

[解]：极板间的电场由极板上的电荷和时变磁场产生。

在工频情况下，忽略时变磁场的影响，即极板间的电场为电准静态场。

在如示坐标系下，得()()()V/m t 31410113t 31410501102d u z 4z 2z e e e E -⨯=-⨯⨯=-=-cos .cos . 由全电流定律得出，即由()z z 20r 4Sl t 31431410113d t H 2d e e S D l H ∙-π⨯⨯-=∙∂∂=π=∙⎰⎰ρεερφsin . 极板间磁场为φφφρe e H t 314103352H 4sin .-⨯== A/m也可以由麦克斯韦方程直接求解磁场强度，如下tt 0r ∂∂=∂∂=⨯∇E D H εε 展开，得t 314106694H 14sin .)(-⨯=∂∂φρρρ 解得φφφρe e H t 314103352H 4sin .-⨯== A/m 讨论：若考虑时变磁场产生的感应电场，则有tt ∂∂-=∂∂-=⨯∇H B E 0μ 展开，得t E z 314cos 103.231440ρμρ-⨯⨯-=∂∂- 解得 t E z 314cos 10537.428ρ-⨯= V/m可见，在工频情况下，由时变磁场产生的感应电场远小于库仑电场。

workbench coupled field static模块介绍
workbench coupled field static模块是COMSOL Multiphysics软
件中的一个模块，用于模拟静态和准静态电磁场。

该模块适用于解决与电磁场静态和准静态行为相关的问题，例如静电荷分布和电场、磁场、电位的计算。

利用workbench coupled field static模块，用户可以对包括电磁
力和电磁耦合效应在内的静电场和磁场进行建模和分析。

该模块支持各种不同的物理现象，包括电场、磁场、静电荷分布、麦克斯韦方程、静电场与电流的相互作用等。

通过设置合适的边界条件和物理参数，用户可以对不同材料和几何形状中的电磁现象进行高度精确的建模和仿真。

workbench coupled field static模块还具有灵活的后处理功能，
可以计算和可视化各种电磁场量，例如电场强度、磁场强度、电势、电磁能量等。

同时，该模块还支持电磁场与其他物理现象（如热传导、结构力学等）的耦合分析。

总而言之，workbench coupled field static模块是一个功能强大
的工具，用于解决静态和准静态电磁场问题，并提供丰富的建模和分析功能，可以应用于多种不同的工程领域和科学研究中。

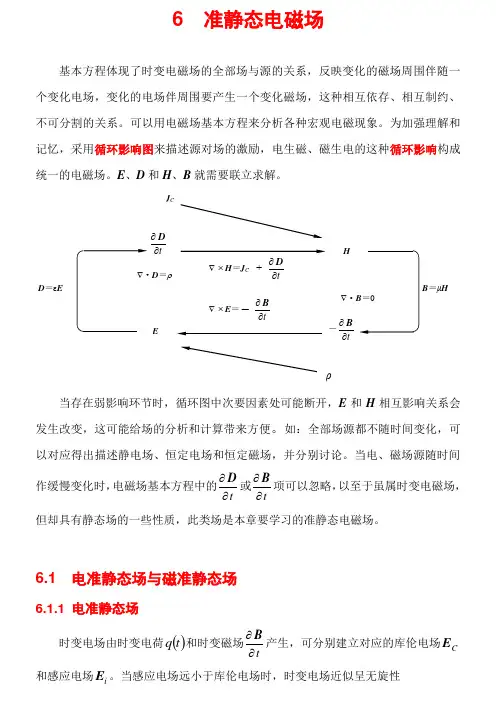
6 准静态电磁场基本方程体现了时变电磁场的全部场与源的关系，反映变化的磁场周围伴随一个变化电场，变化的电场伴周围要产生一个变化磁场，这种相互依存、相互制约、不可分割的关系。

可以用电磁场基本方程来分析各种宏观电磁现象。

为加强理解和记忆，采用循环影响图来描述源对场的激励，电生磁、磁生电的这种循环影响构成统一的电磁场。

E 、D 和H 、B 就需要联立求解。

当存在弱影响环节时，循环图中次要因素处可能断开，E 和H 相互影响关系会发生改变，这可能给场的分析和计算带来方便。

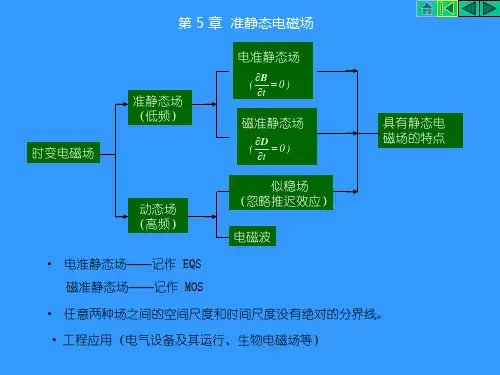
如：全部场源都不随时间变化，可以对应得出描述静电场、恒定电场和恒定磁场，并分别讨论。

当电、磁场源随时间作缓慢变化时，电磁场基本方程中的t ∂∂D 或t∂∂B项可以忽略，以至于虽属时变电磁场，但却具有静态场的一些性质，此类场是本章要学习的准静态电磁场。

6.1 电准静态场与磁准静态场6.1.1 电准静态场时变电场由时变电荷()t q 和时变磁场t∂∂B产生，可分别建立对应的库伦电场CE 和感应电场i E 。

当感应电场远小于库伦电场时，时变电场近似呈无旋性D ＝ρD ＝εEt∂∂D∇ ⨯ H ＝J C +t∂∂DHE∇ ⨯ E ＝－ t∂∂B－t∂∂B∇ ⋅ ρJ CB ＝μH()0=⨯∇≈+⨯∇=⨯∇c i c E E E E即可忽略t∂∂B的作用，称之为电准静态场（Electr oquasistatic ---- EQS ）。

此时电磁场的循环图在E--- t∂∂B 处断开，就每一瞬时而言，磁场不再影响电场，而可以单独地计算电场。

比如E 与场源ρ之间完全对应，只要知道ρ的分布，就可以只运用静电场中计算E 、D 、φ的公式，加上媒质的构成方程，确定出E 、D 和φ等时变电场的场量。

即描述时变电场的方程与静电场方程完全一样，只是E 和D 为时间的函数。

于是，EQS 基本方程的微分形式为t ∂∂+=⨯∇DJ H c （6.1.1） 0≈⨯∇E （6.1.2）0=⋅∇B （6.1.3） ρ=⋅∇D （6.1.4）来求解场量H 、B 等。

电准静态场与磁准静态场电工基础教研室周学本节的研究目的了解准静态场的性质。

本节的研究内容一、电准静态场与磁准静态场二、磁准静态场与电路⎪⎪⎪⎩⎪⎪⎪⎨⎧=⋅∇=⋅∇∂∂-=⨯∇∂∂+=⨯∇f D B tB E tD J H ρ0C 当变化磁场感应出的电场远小于库仑电场时，即0B t ∂≈∂C 00f D D J t B E H ρ⎧⎪∇⋅=⎪⎪⎨∂∇⨯=+⎪∂⎪⎪∇⋅=⎩∇⨯≈与静态场相比，电准静态场具有与静电场类似的有源无旋特性。

因此两种场的计算方法相同。

电力传输系统和装置中的高压电场，各种常用电子器件、设备附近的电场，低频交流情况下，平板电容器中的电场属于电准静态场。

⎪⎪⎪⎩⎪⎪⎪⎨⎧=⋅∇=⋅∇∂∂-=⨯∇∂∂+=⨯∇fD B t BE tD J H ρ0C 当位移电流远小于传导电流时，即0Dt ∂≈∂C0f H B B E t D J ρ⎧⎪∇⋅=⎪⎪⎨∂∇⨯=-⎪∂⎪∇⋅=∇⨯⎪⎩≈与静态场相比，磁准静态场具有与静磁场类同的有旋无源特性。

因此两种场的计算方法相同。

运行于低频情况下的各类电磁装置中的磁场问题(电机、变压器、感应加热装置、磁悬浮等等)、电工技术中的涡流问题属于磁准电磁场。

磁准静态场中的位函数引出与时变电磁场相同22(0)Cf A J A μρϕε⎧∇=-∇⋅=⎪⎨∇=-⎪⎩即在准静态电磁场中，可以略去电磁场的波动性，认为场和源之间具有类似于静态场中场和源之间的“瞬时”对应关系。

磁准静态场也称作似稳场。

⎭⎬⎫≡⨯∇⋅∇=⋅∇0)(0A BAB ⨯∇=⇒⎪⎭⎪⎬⎫≡∇⨯∇∂∂-=⨯∇0ϕt B E ϕ∇-∂∂-=⇒tA E似稳条件：对于导体内的时变电磁场来说，当，导体中的时变电磁场可按磁准静态场来处理。

通常把导体中的磁准静态场称作涡流场。

ωεγ<<对于理想介质中的时变电磁场来说，当或，理想介质中的时变电磁场可按磁准静态场来处理。

即如果系统用准静态方法处理，载流系统的尺寸必须远小于电磁波的波长。

写出微分形式的磁准静态场的麦克斯韦方程组。

麦克斯韦方程组用来求解磁准静态场的极化问题，它是一组连续的作用于某一特定领域上变量的偏微分方程，可以用来求解物理量在该特定领域上的分布情况。

磁准静态场是一种有序的、自发而无他力生成的电场，主要表现为有序、同向的电压差分。

微分形式的麦克斯韦方程组：
1.守恒方程：
∇·E=ρ/ε , 其中ρ表示电介质中固体物质所形成的电荷密度，ε为介质中相对介电常数。

2.电场不变式：∇×E=0 , 表明E场是完备的无旋的向量场。

3.法曲式：∇×B=μ×J , 其中μ为真对气体中相对磁导率。

J为真对气体中因外
界作用产生回流电流所形成的回流电流密度。

4.磁通闭合不变式：∇·B=0, 表明B场是完备无旋向量场。

由以上几个偏微分方程，我们可以求解磁准静态场的物理量在指定区域内的分布情况。

可以看出，磁准静态场的微分形式的麦克斯韦方程是一组复杂的偏微分方程。

此外，我们还可以求解电场、磁场及其他相关物理量在空间上的分布情况，从而更好地理解磁准静态场中的物理本质。