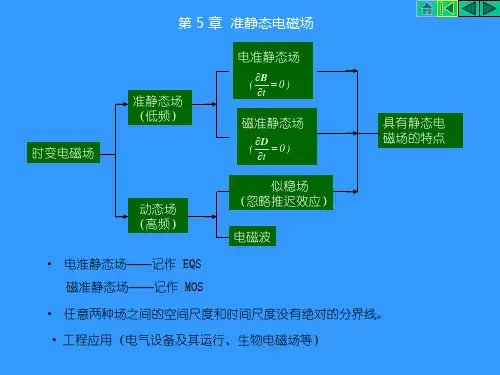
第五章准静态电磁场
- 格式:ppt
- 大小:2.72 MB
- 文档页数:57







第五章习题答案5-2 如题图所示,一半径为a 的金属圆盘,在垂直方向的均匀磁场B 中以等角速度ω旋转,其轴线与磁场平行。
在轴与圆盘边缘上分别接有一对电刷。
这一装置称为法拉第发电机。
试证明两电刷之间的电压为22ωBa 。
证明:,选圆柱坐标, ρφe vB e B e v B v E z ind=⨯=⨯=其中 φρωe v=22ωρρωρερρa B d B e d e v B l d E aal ind====⎰⎰⎰∙∙∴证毕 5-3解:5-4 一同轴圆柱形电容器,其内、外半径分别为cm r 11=、cm r 42=,长度cm l 5.0=,极板间介质的介电常数为04ε,极板间接交流电源,电压为V t 10026000u πsin =。
求s t 0.1=时极板间任意点的位移电流密度。
解法一:因电源频率较低,为缓变电磁场,可用求静电场方法求解。
忽略边沿效应,电容器中的场为均匀场,选用圆柱坐标,设单位长度上内导体的电荷为τ,外导体电荷为τ-,因题图5-2zvρ此有ρρπετe 2E 0=21r r <<ρ1200222121r r d dl E u r r r r lnπετρρπετ===⎰⎰∙1202r r u ln=∴πετ所以ρρer r u E 12 ln =, ρρεer r u D 12ln=2A/mρρππρερεe t 10010026000r r e tu r r tD J 1212dcos ln ln ⨯=∂∂=∂∂=当s t 1=时2512A/m10816100100260004108584ρρρππρe e J d--⨯=⨯⨯⨯⨯=.cos ln .解法二:用边值问题求解,即⎪⎩⎪⎨⎧=====∇401u 02ρϕρϕϕ 由圆柱坐标系有0)(1=∂∂∂∂ρϕρρρ(1)解式(1)得 21ln c c +=ρϕ由边界条件得: 4u c 1ln -= u c 2=u 4u +-=∴ρϕln ln所以 ρρπϕe 4t10026000Eln sin =-∇=ρρπεεe 4t 100260004E D 0ln sin ==ρπρπεe 1004t 100260004t D J 0D⨯=∂∂=ln cos当s t 1=时)(.25D mAe 10816J ρρ-⨯=5-5由圆形极板构成的平板电容器)(d a >>见题图所示,其中损耗介质的电导率为γ、介电系数为ε、磁导率为μ,外接直流电源并忽略连接线的电阻。