高中数学必修4三角函数综合测试题

必修四三角函数与解三角形综合测试题（本试卷满分150分，考试时间120分）第Ⅰ卷（选择题 共40分）一．选择题（本大题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的） 1.若点P 在32π的终边上，且OP=2，则点P 的坐标（ ） A ．)3,1( B ．)1,3(- C ．)3,1(-- D ．)3,1(-2.已知=-=-ααααcos sin ,45cos sin 则（ ）A ．47 B ．169- C ．329- D ．3293.下列函数中，最小正周期为2π的是（ ） A ．)32sin(π-=x y B ．)32tan(π-=x y C ．)62cos(π+=x y D ．)64tan(π+=x y4.等于则)2cos(),,0(,31cos θππθθ+∈=（ ）A ．924-B ．924C ．97- D ．97 5．函数y ＝sin （π4 －2x )的单调增区间是 （ ）A.［kπ－3π8 ，kπ＋π8 ］(k ∈Z )B.［kπ＋π8 ，kπ＋5π8 ］(k ∈Z )C.［kπ－π8 ，kπ＋3π8 ］(k ∈Z )D.［kπ＋3π8 ，kπ＋7π8 ］(k ∈Z )6.将函数x y 4sin =的图象向左平移12π个单位，得到)4sin(ϕ+=x y 的图象，则ϕ等于( )A ．12π-B ．3π-C ．3πD ．12π7. 50tan 70tan 350tan 70tan -+的值等于( )A ．3B ．33C ．33-D ．3-8．在△ABC 中，sinA ＞sinB 是A ＞B 的( )A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件 9.ABC ∆中，π=A ，BC ＝3，则ABC ∆的周长为（ ）A ．33sin 34+⎪⎭⎫ ⎝⎛+πB B ．36sin 34+⎪⎭⎫ ⎝⎛+πBC ．33sin 6+⎪⎭⎫ ⎝⎛+πBD ．36sin 6+⎪⎭⎫ ⎝⎛+πB10．已知0≤x ≤π，且－12 ＜a ＜0，那么函数f (x )＝cos 2x －2a sin x －1的最小值是 （ ）A.2a ＋1B.2a －1C.－2a －1D.2a11．已知函数)sin(φϖ+=x A y 在同一周期内，当3π=x 时有最大值2，当x=0时有最小值-2，那么函数的解析式为 （ ）A ．x y 23sin 2=B ．)23sin(2π+=x y C ．)23sin(2π-=x y D ．x y 3sin 21=12．求使函数y ＝sin(2x ＋θ)＋ 3 cos(2x ＋θ)为奇函数，且在［0，π4 ］上是增函数的θ的一个值为 （ ） A. 5π3B. 4π3C. 2π3D. π3第Ⅱ卷（非选择题 共110分）二．填空题（本大题共4小题，每小题5分，共20分，把答案填在题中横线上） 13.在ABC ∆中，若120A ∠=，5AB =，7BC =，则ABC ∆的面积S ＝_________14.已知,1)cos(,31sin -=+=βαα则=+)2sin(βα _______．15.ΔABC 的三内角,,A B C 所对边的长分别为,,a b c 设向量(,)p a c b =+,(,)q b a c a =--,若//p q ,则角C 的大小为 _．16.函数x x y 2cos )23cos(--=π的最小值为_____．三．解答题（本大题共6小题，共70分。

必修四《三角函数》测试题一、选择题(本大题共10小题,每小题5分，共50分) 1.下列命题正确的是（ D ）.A.终边相同的角都相等B.钝角比第三象限角小C.第一象限角都是锐角D.锐角都是第一象限角 2.若角︒600的终边上有一点()a ,4-，则a 的值是（ A ）.A.34-B.34±C.3D.34B ）. A.3cos5πB.3cos5π-C.3cos5π± D.2cos 5π 4.下列函数中，最小正周期为π，且图象关于直线3x π=对称的是（ C ）.A.)62sin(+=x yB.sin()26x y π=+C.sin(2)6y x π=-D.sin(2)3y x π=-5.设tan()2απ+=，则sin()cos()sin()cos()αααα-π+π-=π+-π+（ A ）.A.3B.13C.1D.1-6.函数y =的定义域是( D ）. A.2,2()33k k k Z ππππ-+∈⎡⎤⎢⎥⎣⎦ B.2,2()66k k k Z ππππ-+∈⎡⎤⎢⎥⎣⎦C.22,2()33k k k Z ππππ++∈⎡⎤⎢⎥⎣⎦D.222,2()33k k k Z ππππ-+∈⎡⎤⎢⎥⎣⎦7. 定义在R 上的函数)(x f 既是偶函数又是周期函数，若)(x f 的最小正周期是π，且当[0,]2x π∈时，x x f sin )(=，则5()3f π的值为（ B ）.A.21-B.23 C.23- D.21 8.函数2sin(2)6y x π=-（[0,]x ∈π）的单调递增区间是（ C ）. A.[0,]3π B.7[,]1212ππ C.5[,]36ππ D.5[,]6ππ9. 若角α的终边落在直线0=+y x 上，则ααααcos cos 1sin 1sin 22-+-的值等于（ D ） A ．2 B ．2- C ．2-或2 D ．010.设a 为常数，且1>a ，02x ≤≤π，则函数1sin 2cos )(2-+=x a x x f 的最大值为（ B ）. A.12+a B.12-a C.12--a D.2a二、填空题(本大题共7小题，每小题5分，共35分. 把答案填在题中的横线上.) 11．与02013-终边相同的最小正角是___147 __；最大负角是___213-_______ ____ 12.在扇形中，已知半径为8，弧长为12，则圆心角是23弧度，扇形面积是 48 .13.方程x x lg sin =的解的个数为__3________.14. 化简：0360sin 270cos 180sin 90cos 0tan r q p x m ---+=____ 0； ________15. 若(cos )cos 2,(sin)______6f x x f π==则12-16.若角α与角β的终边关于y 轴对称，则α与β的关系是________()(21),k k z αβπ+=+∈17.设()s i n ()c o s (f x a x b x αβ=π++π+，其中βα,,,b a 为非零常数. 若(2013)1f =-，则(2014)f = 1 . 三、解答题(本大题共5小题，共65分，解答应写出必要的文字说明、证明过程及演算步骤.)18.（本小题满分12分）已知α是第三角限角，化简ααααs i n 1s i n 1s i n 1s i n 1+---+.解：∵α是第三角限角， ∴0s i n 1>+α，0s i n 1>-α，0c o s <α，∴)s i n 1)(sin 1()sin 1()sin 1)(sin 1()sin 1(sin 1sin 1sin 1sin 122αααααααααα-+-++-+=+---+αααααααα22222222c o s )s i n 1(c o s )s i n 1(s i n 1)s i n 1(s i n 1)s i n 1(--+=----+=ααααααααcos sin 1cos sin 1|cos sin 1||cos sin 1|-++-=--+= αααtan 2cos sin 2-=-=.19.（本小题满分12分）（1）当3tan =α，求αααcos sin 3cos 2-的值；（2）设3222cos sin (2)sin()32()22cos ()cos()f θθθθθθπ+π-++-=+π++-，求()3f π的值. 19.解：（1）因为1tan tan 31cos sin cos sin 3cos cos sin 3cos 22222+-=+-=-αααααααααα， 且3tan =α， 所以，原式=+⨯-=13331254-. （2）θθθθθθθπθπθπθθcos cos 223cos sin cos 2)cos()(cos 223)2sin()2(sin cos 2)(223223++-++=-+++-++-+=fθθθθθθθθθθθθcos cos 22)1(cos cos )1cos )(cos 1(cos 2cos cos 222cos cos cos 222223++--++-=++-+-=1cos 2cos cos 2)2cos cos 2)(1(cos 22-=++++-=θθθθθθ， ∴1()cos1332f ππ=-=-. 20.（本小题满分12分）已知函数())4f x x π=-，x ∈R ．(1)求函数()f x 的最小正周期和单调递增区间；(2)求函数()f x 在区间[]82ππ-，上的最小值和最大值，并求出取得最值时x 的值.20.解：（1）因为())4f x x π=-，所以函数()f x 的最小正周期为22T π==π，由2224k x k π-π+π≤-≤π，得388k x k ππ-+π≤≤+π，故函数)(x f 的递调递增区间为3[,]88k k ππ-+π+π（Z k ∈）；(2)因为())4f x x π=-在区间[]88ππ-，上为增函数，在区间[]82ππ，上为减函数，又()08f π-=，()8f π=π())1244f ππ=π-==-，故函数()f x 在区间[]82ππ-，8x π=；最小值为1-，此时2x π=．21.（本小题满分14分）已知()2sin(2)26f x a x a b π=-+++，3[,]44x ππ∈，是否存在常数Q b a ∈,，使得)(x f 的值域为}133|{-≤≤-y y ？若存在，求出b a ,的值；若不存在，说明理由.21.解：存在1-=a ，1=b 满足要求. ∵344x ππ≤≤， ∴252363x πππ≤+≤，∴1sin(2)6x π-≤+≤， 若存在这样的有理b a ,，则（1）当0>a 时，⎪⎩⎪⎨⎧-=++-=++-,1322,323b a a b a a 无解；（2）当0<a 时，⎩⎨⎧-=++--=++,1323,322b a a b a a 解得1-=a ，1=b ，即存在1-=a ，1=b 满足要求.22.（本小题满分14分）已知函数()()()sin 0,0f x A x B A ωϕω=++>>的一系列对应值如下表：（1）根据表格提供的数据求函数()f x 的一个解析式； （2）根据（1）的结果，若函数()()0y f kx k =>周期为23π，当[0,]3x π∈时，方程()f kx m =恰有两个不同的解，求实数m 的取值范围.22. 解：（1）设()f x 的最小正周期为T ，得11()266T ππ=--=π， 由2T ωπ=，得1ω=，又31B A B A +=⎧⎨-=-⎩，解得21A B =⎧⎨=⎩ 令562ωϕππ⋅+=，即562ϕππ+=，解得3ϕπ=-， ∴()2sin 13f x x π⎛⎫=-+ ⎪⎝⎭. （2）∵函数()2sin 13y f kx kx π⎛⎫==-+ ⎪⎝⎭的周期为23π，又0k >， ∴3k =， 令33t x π=-，∵0,3x π⎡⎤∈⎢⎥⎣⎦， ∴2[,]33t ππ∈-，如图，s t =sin 在2[,]33ππ-上有两个不同的解，则)1,23[∈s ，∴方程()f kx m =在[0,]3x π∈时恰好有两个不同的解，则)1,3m ∈，即实数m 的取值范围是)1,3。

必修4三角函数综合测试题及答案详解一、选择题1 •下列说法中，正确的是（）A. 第二象限的角是钝角B. 第三象限的角必大于第二象限的角C. —831 °是第二象限角D. —95° 20', 984° 40', 264° 40'是终边相同的角a n2.若点（a, 9）在函数y = 3x的图象上，贝U tang的值为（）A. 0B. -3 C . 1 D. 33g3 .若|cos g | = cos g , |tan g | = —tan B ,则㊁的终边在（）A. 第一、三象限B. 第二、四象限C•第一、三象限或x轴上D.第二、四象限或x轴上4 .如果函数f（x）= sin（n x + B ）（0< B <2n ）的最小正周期是T,且当x = 2时取得最大值，那么（）A. T= 2, n 十g= ~ B . T= 1, g = nC. T= 2,n g = n D . T= 1, g=5 .若sin—x =—于，且n<xv2n,则x 等于（）4 A.§n7 B・6nc.)小11 D.§n6 .已知a是实数，而函数f （x）= 1 + asin ax的图象不可能是（）7.将函数y = sin x的图象向左平移© (0 < © <2n )个单位长度后，得到yn=sin x-~6的图象，贝U ©=( )7n 11 n8.若tan 9 = 2,则2sin B —cosBsin 9 + 2cos 9的值为(A. 0B. 1D.5tan x9.函数f(x)= 的奇偶性是()1 + cosx ' /A. 奇函数B. 偶函数C•既是奇函数又是偶函数D.既不是奇函数也不是偶函数10.函数f(x) = x —cosx 在(0,+x)内()A.没有零点B•有且仅有一个零点C. 有且仅有两个零点D. 有无穷多个零点11 _ cosA = n 贝U igsin A 的值是( B. m- n 1D ・2(m- n)n12. 函数f (x) = 3sin 2x -空 的图象为C,n 5 n② 函数f (x )在区间—12,刁2内是增函数;n③由y 二3sin2x 的图象向右平移 ㊁个单位长度可以得到图象C,其中正确命 题的个数是( )A. 0B. 1C. 2D. 3二、填空题(本大题共4小题，每题5分，共20分.将答案填在题中横线上)- n 1 n ,13. ___________________________________________________ 已知 sin a +~2 = 3， a € —-^, 0，则 tan a = ________________________________ .14. 函数y = 3cosx(0 <x <n )的图象与直线y = — 3及y 轴围成的图形的面 积为 ________ .15 .已知函数f (x) = sin( 3x + © )( 3 >0)的图象如图所示，贝U 3 =16. 给出下列命题:① 函数y = cos / +专 是奇函数;11.已知 A 为锐角,lg(1 + cosA) = m ig 1A. RH-①图象C 关于直线x =11n 12 对称;②存在实数x,使sinx + cosx = 2；③若a , B是第一象限角且a <B ,贝U tan a <tan B ;④ X = nn 是函数y = sin 2X + 5n 的一条对称轴;nn⑤ 函数y = sin 2X + -3的图象关于点12， 0成中心对称.其中正确命题的序号为 __________ . 三、解答题17. (10 分)已知方程 sin( a -3n ) = 2cos( a -4n ),n 32sinn —a 3n+ 5cos 2 n — a的18.a — sin（12 分）在^ ABC 中, sin A + cosA = _22求tan A 的值.19. （12 分）已知f（x）= sin 2X+6 + 2, x€ R.(1) 求函数f(x)的最小正周期；(2) 求函数f(x)的单调减区间；(3) 函数f (x)的图象可以由函数y= sin2x(x € R的图象经过怎样变换得到？n20. (12 分)已知函数y = Asi n( ”+© )( A>0, co >0)的图象过点P^, 0 ,n图象与P点最近的一个最高点坐标为nn, 5 .(1)求函数解析式；⑵求函数的最大值，并写出相应的x的值;(3)求使y W0时，x的取值范围.21. （12 分）已知cos nn —a = 2cos 3 n+B , 3sin —an=—• 2s in — + B，且0< a <n, 0< B <n,求a , B 的值.22. (12 分)已知函数f(x) = x2+ 2xtan 9 —1, x € ［—1, 3］，其中n n-T , y.n(1)当9 =——时，求函数的最大值和最小值；⑵求9的取值范围，使y = f(x)在区间［—1, .3］上是单调函数(在指定区间为增函数或减函数称为该区间上的单调函数).必修4三角函数综合测试题答案可知 COS aM 0. sin a + 5cos a•原式—一2C0S a + Sin a—2cos a + 5cos a 3COS a——2cos a — 2cos a — — 4COS a — x/2 18 .解 I sin A + cosA =-^，①1两边平方，得2sinAcosA = — 2,n 从而知 cosAvO,'./ A € —, n••• si nA — cosA = ,： sin A + cosA 2— 4s in AcosA 由①②，得 sinA -cosA — — 6+，2,sin A厂、 选择题1. D;2.；3. D;4. A ;5.6.D 7. D ;8.C ; 9.A ; 10.11. D; 12. C二_ 填空题13. —2.2 1 4. 33n; 15.2；三、 解答题17. 解 T sin( a — 3 n ) — 2cos( a — 4• — sin(3 n 一 a ) — 2cos(4 n —a•• — sin( n- —a)—2cos( — a ).①④3 4. BB 16.n )• • sin a —•tanA二cosA—2- 3.小n21.解cos ——a = 2cos 3n+ B ,即sin a = 2sin B ①3sin 3n— a=—2sin ,即，3cos a = 2cos B ②22 2 2n19. 解(1)T=_y 二n.n n 3 n(2)由2k n + — <2x + — <2 k 冗+, k € Z,n , 2 n ,得k n + x < k n + , k € Z.6 3所以所求的单调减区间为, n , 2 nk 冗+石,k n+~^(k€ Z).n3⑶把y二sin2x的图象上所有点向左平移厉个单位，再向上平移3个单位，即得n3函数f (x) = sin 2x +石+ 2的图象.T n n n20. 解(1)由题意知4="3—12="4，••• T=n.2 n . n /口n —"•①=~T = 2，由3 • 12+ © = 0，得© = —"6，又A= 5，n•y = 5sin 2x —百.n n⑵函数的最大值为5,此时2x —石=2k n+ y(k € Z).・ n .•x = k n+"3(k € Z).n ■n . .(3) - 5sin 2x —< 0,・• 2k n — n<2 x —<2 k n( k € Z)., 5 n , n ,• k n-在 < x< k n+/(k € Z).9=-_6 时， 2 2 ； 3 , 3 2 4 =x -亍-1= x -§ - v x € [ - 1, .3],二当 x = f 时，f(x)的最小值为一3 ,⑵f (x) = (x + tan 9 )2-1-tan 2 9是关于x 的二次函数.它的图象的对称轴为x =—tan 9 .又 v a € (0 ,n ) , — a n、 =N , 或 a 3 =—n 4n ■n f, 当 a ==时，COS a 4€ (0 ,n ), 5 n ，宀「 :B = -y.综上， ~6，或a 3n ， 5 n B =〒 22. f(x) 当x =- 1时，f(x)的最大值为 2,3 3 . ¥，COS ⑵ cos B COS a =当v y= f(x)在区间［-1, 3］上是单调函数,/• —tan 9 <—1,或一tan 9 > _ 3,即卩tan 9 > 1,或tan 9<-,3.nnn，二9的取值范围是n n 2，一3。

高一数学必修4三角函数试题一、选择题（本大题10小题，每小题5分，共50分．只有一项是符合题目要求的）1.cos(60)-的值是 （ ）A.12B.12- C. D. 2.下列函数是偶函数且周期为π的是 （ ）A. sin y x =B. cos y x =C.tan y x =D. cos 2y x =3.已知sin 0,cos 0θθ<>，则θ的终边在 （ ）A.第一象限B. 第二象限C. 第三象限D. 第四象限4.函数()sin f x x =的周期为 （ ）A. πB. 2πC. 3πD. 4π 5.已知sin(),cos(),tan()654a b c πππ=-=-=-，则大小关系为 （ ） A. a b c << B. c a b << C. b a c << D. c b a << 6.已知扇形的半径为3，圆心角为120°，则扇形的弧长和面积分别为 （ ）A.π、2πB. 2π、3πC. 3π、4πD. 4π、4π7.集合{sin }A y y x ==,{cos }B y y x ==，下列结论正确的是 （ ）A. A B =B. A B ⊆C. [1,0)A C B =-D. [1,0]A C B =-8.下列关于正切函数tan y x =的叙述不正确的是 （ ）A.定义域为{,}2x x k k Z ππ≠+∈ B. 周期为πC.在(,),22k k k Z ππππ-++∈上为增函数 D.图象不关于点(,0)2k π，k Z ∈对称 9.下列关系式成立的是 （ ）A.sin(3)sin παα+= B .tan(5)tan παα-= C.3cos()sin 2παα+= D.3sin()cos 2παα-= 10. 下列不等式成立的是 （ ）A. sin1cos1<B. sin 2cos2<C. sin3cos3<D. sin 4cos4<第Ⅱ卷（非选择题 共100分）二、填空题：本大题共5小题，每小题5分，共25分.把答案填在题中横线上.11.函数2sin(3)6y x π=+的最大值为 . 12.已知1cos 3α=，则sin()2πα-= . 13.已知tan 1α=，(,2)αππ∈，则cos α= .14.函数()sin(3)f x x π=+的最小正周期为 .15.已知sin()y A x ωϕ=+(0,0,)2A πωϕ<><的部分图象，则y = .三、解答题：本大题共6小题，共75分，解答题应写出文字说明、证明过程或演算步骤。

三角函数单元测试一、选择题(12小题60分)1、将分针拨慢5分钟，则分钟转过的弧度数是 ( C ),,,, A( B(, C( D(, 3366P(sin,cos,,2cos,)2、如果点位于第三象限，那么角所在象限是 ( B ) ,,、第一象限 B、第二象限 C、第三象限 D、第四象限 3、已知角的终边经过点(，)()，则的值是 ( B ) P,4m3mm,02sin,，cos,,2221或 (B)或 (C)1或 (D) (A),1,1,,555,4、要得到的图象只需将y=3sin2x的图象 ( C ) y,3sin(2x，)4,,A(向左平移个单位 B(向右平移个单位 44,,C(向左平移个单位 D(向右平移个单位 885、如图，曲线对应的函数是 ( C ) A(y=|sinx| B(y=sin|x| C(y=,sin|x| D(y=,|sinx|12A6、为三角形ABC的一个内角,若,则这个三角形形状为 ( B )sincosAA，,25A. 锐角三角形B. 钝角三角形C. 等腰直角三角形D. 等腰三角形,7、函数的图象 ( B ) y,2sin(2x，)3,,A(关于原点对称 B(关于点(,，0)对称 C(关于y轴对称 D(关于直线x=对称668、函数的定义域是 ( D ) yx,，2cos1,,,,，，，，2,2()kkkZ,，,2,2()kkkZ,，,A( B( ,,,,,,,,3366，，，，,,222,,，，，，，，,,，,2,2()kkkZ2,2()kkkZC( D( ,,,,,,,,3333，，，，,9(函数的单调递减区间是 ( C ) y,sin(,2x，)6,,5,,(，2k,,，2k,]k,ZA( B( [,，2k,,，2k,]k,Z6366,,5,,C( D( [，k,,，k,]k,Z(,，k,,，k,)k,Z6663,,2210(函数的最小正周期为 ( C ) y,cos(x,)，sin(x，),11212,,A( B( C( D( 2,,42411(把函数的图象向右平移个单位，所得图象正好关于轴对称，则,y,y,cos(x，),3的最小正值是 ( C )4215A( B( C( D( ,,,,3333y,2cosx(0,x,2,)y,212(把函数的图象和直线围成一个封闭的图形，则这个封闭图形的面积为 ( D )A(4 B(8 C(2 D(4 ,,二、填空题:共4小题，把答案填在题中横线上((20分) ,,2113、函数的最小值是 y,cos(x,)(x,[,,])286313,,,14、已知则 cos,,sin,,sin,cos,,且,,,,,,2842cos15:sin9:，sin6:15( ,3,2sin15:sin9:,cos6:,,16、不等式的解集是 {x/,，k,,x,，k,,k,Z}1，3tanx,062三、解答题:共6小题，解答应写出文字说明、证明过程或演算步骤(317、(10分)已知,求的值. sincos,,,,,,,,,,tan3,23解: ,,,,,,,且tan3,2,3,sin,,,,sin3cos,,,13,,,2？,,sincos,,？,,sin0,cos0,,，由得 ,,2221sincos1，,,,,,,cos,,,,,2,,,12318、(12分)已知，且，. ,,,,,,,,，,,,,,cos()sin()24135,,,,,，,(1)求的取值范围;cos2,(2)求的值.,,,,,,,,,解:(1)由，得，又， ,,,,,,,,,,,,,,244224,,,,,,,0两式相加有，而，?0， ,,,,,,,,,,,444,,,,,,,,由与相加得， ,,,,,,,,,,，,24242,,,?，; (0,)(),,,,,,，,,～421253422,,,,,,cos()1(),,，,,,,,,sin()1()(2)由(1)及已知得，， 551313 cos2cos[()()],,,,,,，,,?cos()cos()sin()sin(),,,,,,,,，,，，, =4123563 = =. ,()(),，，,，655135133xx19((12分)已知函数 f(x),(cos，3sin)，3.222(1)用五点法画出它在一个周期内的闭区间上的图象;f(x)(2)指出的周期、振幅、初相;(3)说明此函数图象可由上的图象经怎样的变换得到. y,sinx在[0,2,]解: (1)略.,,(2)A=3，T=4，( ,,6(3)略.20((12分)将一块圆心角为60?，半径为20cm的扇形铁电裁成一个矩形，求裁得矩形的最大面积.2020sin,MN,20cos,sin,,,，P0N,,解: 如图设，则PN=，320 S=， MNPQ20sin,(20cos,,sin,)3,,30:当时，2003S取最大值 MNPQ321. (本小题满分12分)2已知函数 fxxx()sin22sin,,fx()(I)求函数的最小正周期。

高一必修4三角函数部分综合测试卷（满分150分，时间120分钟）一、选择题：（每小题5分共计60分）1.sin α=错误！未找到引用源。

,α∈错误！未找到引用源。

,则cos α= ( )A.- 错误！未找到引用源。

B.错误！未找到引用源。

C.错误！未找到引用源。

D.-错误！未找到引用源。

2．在（0，2π）内，x x cos sin >成立的x 的取值范围（ ）A. )45;()2,4(ππππ B.),4(ππ C . )45,4(ππ D. )23,45(),4(ππππ3．已知角α的终边与单位圆交于点错误！未找到引用源。

,则sin2α的值为 ( ) A.错误！未找到引用源。

B.-错误！未找到引用源。

C.- 错误！未找到引用源。

D.错误！未找到引用源。

4. sin89cos14sin1cos76-=（ ）A45．=+-)12sin12(cos)12sin12(cosππππ( )A. 23-B. 21-C. 21 D . 236.将函数sin(2)ϕ=+y x 的图象沿x 轴向左平移8π个单位后，得到一个偶函数 的图象，则ϕ的一个可能取值为 ( )(A) 34π (B) 4π (C) 0 (D) 4π-7、函数cos sin =+y x x x 的图象大致为（ ）A B C D8．在ABC ∆中，2sin sin cos2AB C =，则ABC ∆一定是（ ） A ．直角三角形 B ．等腰三角形 C ．等腰直角三角形 D ．正三角形9．=-+0tan50tan703tan50tan70 （ ）A.3 B.33 C. 33- D. 3-10．要得到函数x y 2sin =的图象，可由函数)42cos(π-=x y （ ）A. 向左平移8π个长度单位 B. 向右平移8π个长度单位 C. 向左平移4π个长度单位 D. 向右平移4π个长度单位11．设tan α,tan β是方程x 2-3x+2=0的两个根,则tan(α+β)的值为( )A .-3 B.-1 C.1 D.312．若均βα,为锐角，==+=ββααcos ,53)(sin ,552sin 则（ ） A.552 B. 2552 C. 2552552或 D. 552-二、填空题：（每小题5分共计20分） 13.函数)62sin(π+-=x y 的单调递减区间是________________________；14. 已知函数)52sin()(ππ+=x x f ，若对任意R x ∈都有)()()(21x f x f x f ≤≤成立，则||21x x -的最小值是____________；15．设sin 2sin αα=-，(,)2παπ∈，则tan 2α的值是____________；16. 已知βα,为锐角, 的值为则βαβα+==,51cos ,101cos .三、解答题：（6道小题共计70分）17．（10分）如图,在平面直角坐标系xOy 中,以Ox 轴为始边作两个锐角α,β,它们的终边分别与单位圆相交于A,B 两点.已知A,B 的横坐标分别为错误！未找到引用源。

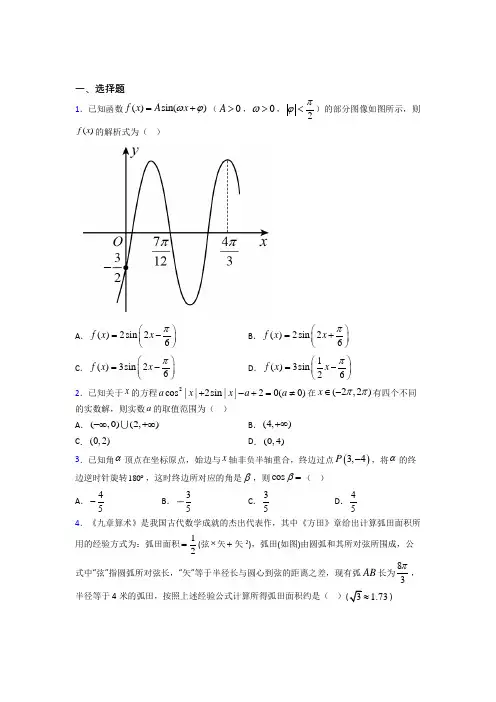
一、选择题1．已知函数()sin()f x A x ωϕ=+（0A >，0>ω，2πϕ<）的部分图像如图所示，则()f x 的解析式为（ ）A ．()2sin 26f x x π⎛⎫=- ⎪⎝⎭B ．()2sin 26f x x π⎛⎫=+ ⎪⎝⎭C ．()3sin 26f x x π⎛⎫=-⎪⎝⎭D ．1()3sin 26f x x π⎛⎫=-⎪⎝⎭ 2．已知关于x 的方程2cos ||2sin ||20(0)+-+=≠a x x a a 在(2,2)x ππ∈-有四个不同的实数解，则实数a 的取值范围为（ ） A ．(,0)(2,)-∞+∞B ．(4,)+∞C ．(0,2)D ．(0,4)3．已知角α顶点在坐标原点，始边与x 轴非负半轴重合，终边过点()3,4P -，将α的终边逆时针旋转180︒，这时终边所对应的角是β，则cos β=（ ） A ．45-B ．35C ．35D ．454．《九章算术》是我国古代数学成就的杰出代表作，其中《方田》章给出计算弧田面积所用的经验方式为：弧田面积12=(弦⨯矢+矢2)，弧田(如图)由圆弧和其所对弦所围成，公式中“弦”指圆弧所对弦长，“矢”等于半径长与圆心到弦的距离之差，现有弧AB 长为83π，半径等于4米的弧田，按照上述经验公式计算所得弧田面积约是（ ）3 1.73≈)A ．6平方米B ．9平方米C ．12平方米D ．15平方米5．函数1sin3y x =-的图像与直线3x π=，53x π=及x 轴所围成的图形的面积是（ ） A ．23π B ．πC ．43π D ．53π 6．已知奇函数()f x 满足()(2)f x f x =+，当(0,1)x ∈时，函数()2x f x =，则12log 23f ⎛⎫= ⎪⎝⎭（ ） A ．1623-B ．2316-C ．1623D ．23167．《九章算术》中《方田》章有弧田面积计算问题，术日：以弦乘矢，矢又自乘，并之，二而一．其大意是弧田面积计算公式为：弧田面积12=(弦×矢+矢×矢)．弧田是由圆弧(弧田弧)及圆弧两端点的弦(弧田弦)围成的平面图形，公式中的“弦”指的是弧田弦的长，“矢”指的是弧田所在圆的半径与圆心到孤田弦的距离之差，现有一弧田，其矢长等于8米，若用上述弧田面积计算公式算得该弧田的面积为128平方米，则其弧田弧所对圆心角的正弦值为（ ） A ．60169B ．120169C ．119169D ．591698．已知函数()[][]sin cos cos sin f x x x =+，其中[]x 表示不超过实数x 的最大整数，则（ ）A ．()f x 是奇函数B ．π2π33f f ⎛⎫⎛⎫<⎪ ⎪⎝⎭⎝⎭C ．()f x 的一个周期是πD ．()f x 的最小值小于09．下列函数中，既是偶函数，又在(),0-∞上是增函数的是（ ） A ．()22xxf x -=- B ．()23f x x =-C ．()2ln =-f x xD ．()cos3=f x x x10．现有四个函数：①y =x |sin x |，②y =x 2cos x ，③y =x ·e x ；④1y x x=+的图象(部分)如下，但顺序被打乱，则按照从左到右将图象对应的函数序号安排正确的一组是（ ）A ．①②③④B ．①③②④C ．②①③④D ．③②①④11．若函数()22()sin 23cos sin f x x x x =+-的图像为E ，则下列结论正确的是（ ） A ．()f x 的最小正周期为2π B ．对任意的x ∈R ，都有()()3f x f x π=-C ．()f x 在7(,)1212ππ上是减函数D ．由2sin 2y x =的图像向左平移3π个单位长度可以得到图像E 12．函数22y cos x sinx ＝－ 的最大值与最小值分别为( ) A ．3，－1 B ．3，－2 C ．2，－1D ．2，－2二、填空题13．下列判断正确的是___________(将你认为所有正确的情况的代号填入横线上). ①函数1tan 21tan 2xy x+=-的最小正周期为π；②若函数()lg f x x =，且()()f a f b =，则1ab =； ③若22tan 3tan 2αβ=+，则223sin sin 2αβ-=；④若函数()2221sin 41x xy x ++=+的最大值为M ，最小值为N ，则2M N +=.14．函数()()sin f x x ωϕ=+的部分图象如图所示，则()f x 的单调递增区间为___________．15．sin 75=______．16．如图，从气球A 上测得正前方的B ，C 两点的俯角分别为75︒，30，此时气球的高是60m ，则BC 的距离等于__________m .17．如图，游乐场所的摩天轮匀速旋转，每转一周需要l2min ，其中心O 离地面45米，半径40米.如果你从最低处登上摩天轮，那么你与地面的距离将随时间的变化而变化，以你登上摩天轮的时刻开始计时，请问：当你第六次距离地面65米时，用了________分钟？18．函数251612()sin (0)236x x f x x x x ππ-+⎛⎫=--> ⎪⎝⎭的最小值为_______. 19．关于函数()4sin(2)(),3f x x x R π=+∈有下列命题：①由12()()0f x f x ==可得12x x -必是π的整数倍；②()y f x =的图象关于点(,0)6π-对称；③()y f x =的表达式可改写为4cos(2);6y x π=-④()y f x =的图象关于直线6x π=-对称.其中正确命题的序号是_________. 20．给出下列命题： ①函数()4cos 23f x x π⎛⎫=+⎪⎝⎭的一个对称中心为5,012π⎛⎫-⎪⎝⎭； ②若α，β为第一象限角，且αβ>，则tan tan αβ>；③在ABC ∆中，内角A ，B ，C 所对的边分别为a ，b ，c ，若40a =，20b =，25B =︒，则ABC ∆必有两解.④函数sin 2y x =的图象向左平移4π个单位长度，得到sin 24y x π⎛⎫=+ ⎪⎝⎭的图象.其中正确命题的序号是 _________（把你认为正确的序号都填上）．三、解答题21．已知函数()()1sin 226f x x x R π⎛⎫=+∈ ⎪⎝⎭． （1）填写下表，并用“五点法”画出()f x 在[0,]π上的图象；26x π+6π 136πxπ ()f x（2）将()y f x =的图象向上平移1个单位，横坐标缩短为原来的2，再将得到的图象上所有点向右平移4π个单位后，得到()g x 的图象，求()g x 的对称轴方程． 22．现给出以下三个条件：①()f x 的图象与x 轴的交点中，相邻两个交点之间的距离为2π；②()f x 的图象上的一个最低点为2,23A π⎛⎫- ⎪⎝⎭； ③()01f =.请从上述三个条件中任选两个，补充到下面试题中的横线上，并解答该试题. 已知函数()()2sin 05,02f x x πωϕωϕ⎛⎫=+<<<< ⎪⎝⎭，满足________，________. （1）根据你所选的条件，求()f x 的解析式； （2）将()f x 的图象向左平移6π个单位长度，得到()g x 的图象求函数()()1y f x g x =-的单调递增区间.23．函数()cos()0,02f x x πωϕωϕ⎛⎫=+><<⎪⎝⎭的部分图象如图所示．（1）写出()f x 的解析式； （2）将函数()f x 的图象向右平移12π个单位后得到函数()g x 的图象，讨论关于x 的方程()3()0f x g x m -=(11)m -<≤在区间,2ππ⎡⎤-⎢⎥⎣⎦上的实数解的个数．24．已知函数π()3sin 26f x x ⎛⎫=+⎪⎝⎭． （1）用“五点法”画出函数()y f x =在一个周期内的简图；（2）说明函数()y f x =的图像可以通过sin y x =的图像经过怎样的变换得到？（3）若003()[2π3π]2f x x =∈，，，写出0x 的值. 25．已知函数()sin()0,0,||2f x A x A πωϕωϕ⎛⎫=+>>< ⎪⎝⎭，,28M π⎛⎫⎪⎝⎭､5,28N π⎛⎫- ⎪⎝⎭分别为其图象上相邻的最高点､最低点. （1）求函数()f x 的解析式； （2）求函数()f x 在0,2π⎡⎤⎢⎥⎣⎦上的单调区间和值域. 26．已知函数()2sin(2)(0)6f x x πωω=+>.（1）若点5(,0)8π是函数()f x 图像的一个对称中心，且(0,1)ω∈，求函数()f x 在3[0,]4π上的值域； （2）若函数()f x 在(,)33π2π上单调递增，求实数ω的取值范围.【参考答案】***试卷处理标记，请不要删除一、选择题 1．C解析：C 【分析】 本题首先可根据33π44T 求出ω，然后根据当43x π=时函数()f x 取最大值求出ϕ，最后代入30,2⎛⎫- ⎪⎝⎭，即可求出A 的值. 【详解】因为4π7π3π3124，所以33π44T ，T π=，因为2T πω=，所以2ω=，()sin(2)f x A x ϕ=+，因为当43x π=时函数()sin(2)f x A x ϕ=+取最大值， 所以()42232k k Z ππϕπ⨯+=+∈，()26k k Z πϕπ=-+∈，因为2πϕ<，所以6πϕ=-，()sin 26f x A x π⎛⎫=-⎪⎝⎭， 代入30,2⎛⎫- ⎪⎝⎭，3sin 26A π⎛⎫-=- ⎪⎝⎭，解得3A =，()3sin 26f x x π⎛⎫=- ⎪⎝⎭， 故选：C. 【点睛】关键点点睛：本题考查根据函数图像求函数解析式，对于()sin()f x A x ωϕ=+，可通过周期求出ω，通过最值求出A ，通过代入点坐标求出ϕ，考查数形结合思想，是中档题.2．D解析：D 【分析】令2()cos ||2sin ||2(0)=+-+≠f x a x x a a ，易知函数()f x 是偶函数，将问题转化为研究当(0,2)x π∈时，2()cos 2sin 2=+-+f x a x x a 有两个零点，令sin t x =，则转化为2()22(0)=--≠h t at t a 有一个根(1,1)t ∈-求解.【详解】当(2,2)x ππ∈-，2()cos ||2sin ||2(0)=+-+≠f x a x x a a ，则()()f x f x -=，函数()f x 是偶函数，由偶函数的对称性，只需研究当(0,2)x π∈时，2()cos 2sin 2=+-+f x a x x a 有两个零点，设sin t x =，则2()22(0)=--≠h t at t a 有一个根(1,1)t ∈- ①当0a <时，2()22=--h t at t 是开口向下，对称轴为10t a=<的二次函数，(0)20h =-<则(1)0->=h a ，这与0a <矛盾，舍去；②当0a >时，2()22=--h t at t 是开口向上，对称轴为10t a=>的二次函数， 因为(0)20h =-<，(1)220-=+->=h a a ， 则存在(1,0)t ∈-，只需(1)220=--<h a ，解得4a <， 所以04a <<．综上，非零实数a 的取值范围为04a <<． 故选：D ． 【点睛】方法点睛：已知函数有零点(方程有根)求参数值(取值范围)常用的方法： （1）直接法：直接求解方程得到方程的根，再通过解不等式确定参数范围； （2）分离参数法：先将参数分离，转化成求函数的值域问题加以解决；（3）数形结合法：先对解析式变形，进而构造两个函数，然后在同一平面直角坐标系中画出函数的图象，利用数形结合的方法求解3．B解析：B 【分析】先根据已知条件求解出cos α的值，然后根据,αβ之间的关系结合诱导公式求解出cos β的值. 【详解】 因为3cos 5α==，且180βα=+︒， 所以()3cos cos 180cos 5βαα=+︒=-=-， 故选：B. 【点睛】结论点睛：三角函数定义有如下推广：设点(),P x y 为角α终边上任意一点且不与原点重合，r OP =，则()sin ,cos ,tan 0y x yx r r xααα===≠. 4．B解析：B 【分析】根据已知求出矢2=，弦2AD ==. 【详解】由题意可得：823=43AOB ππ∠=，4OA =，在Rt AOD 中，可得：3AOD π∠=，6DAO π∠=，114222OD AO ==⨯=， 可得：矢422=-=， 由3sin4233AD AO π==⨯=， 可得：弦243AD ==， 所以：弧田面积12=（弦⨯矢+矢221)(4322)43292=⨯+=+≈平方米．故选：B 【点睛】方法点睛：有关扇形的计算，一般是利用弧长公式l r α=、扇形面积公式12S lr =及直角三角函数求解.5．C解析：C 【分析】作出函数1sin3y x =-的图像，利用割补法，补成长方形，计算面积即可. 【详解】作出函数1sin3y x =-的图象，如图所示，利用割补法，将23π到π部分的图象与x 轴围成的图形补到图中3π到23π处阴影部分，凑成一个长为3π，宽为2的长方形，后面π到53π，同理；∴1sin3y x =-的图象与直线3x π=，53x π=及x 轴所围成的面积为24233ππ⨯=，故选：C. 【点睛】用“五点法”作()sin y A ωx φ=+的简图，主要是通过变量代换，设z x ωϕ=+，由z 取0，2π，π，32π，2π来求出相应的x ，通过列表，计算得出五点坐标，描点后得出图象． 6．B解析：B【分析】由已知得到(2)()f x f x +=，即得函数的周期是2，把12(log 23)f 进行变形得到223()16f log -， 由223(0,1)16log ∈满足()2x f x =，求出即可． 【详解】(2)()f x f x +=，所以函数的周期是2.根据对数函数的图象可知12log 230<，且122log 23log 23=-；奇函数()f x 满足(2)()f x f x +=和()()f x f x -=-则2312222223(log 23)(log )(log 23)(log 234)()16f f f f f log =-=-=--=-， 因为223(0,1)16log ∈ 2231622323()21616log f log ∴-=-=-，故选：B ． 【点睛】考查学生应用函数奇偶性的能力，函数的周期性的掌握能力，以及运用对数的运算性质能力．7．B解析：B 【分析】求出弦长，再求出圆的半径，然后利用三角形面积求解． 【详解】如图，由题意8CD =，弓琖ACB 的面积为128，1(8)81282AB ⨯+⨯=，24AB =， 设所在圆半径为R ，即OA OB R ==，则22224(8)2R R ⎛⎫=-+ ⎪⎝⎭，解得13R =， 5OD =，由211sin 22AB OD OA AOB ⨯=∠得 2245120sin 13169AOB ⨯∠==． 故选：B ．【点睛】关键点点睛：本题考查扇形与弓形的的有关计算问题，解题关键是读懂题意，在读懂题意基础上求出弦长AB ，然后求得半径R ，从而可解决扇形中的所有问题．8．D解析：D 【分析】利用奇函数的性质判断A ，分别求3f π⎛⎫⎪⎝⎭和23f π⎛⎫⎪⎝⎭判断大小，取特殊值验证的方法判断C ，分区间计算一个周期内的最小值，判断选项D 。

完整版)高中三角函数测试题及答案高一数学必修4第一章三角函数单元测试班级：__________ 姓名：__________ 座号：__________评分：__________一、选择题：共12小题，在每小题给出的四个选项中，只有一项是符合题目要求的。

（48分）1、已知$A=\{\text{第一象限角}\}$，$B=\{\text{锐角}\}$，$C=\{\text{小于90°的角}\}$，那么$A$、$B$、$C$ 关系是（）A．$B=A\cap C$B．$B\cup C=C$C．$A\cap D$D．$A=B=C$2、将分针拨慢5分钟，则分钟转过的弧度数是A。

$\frac{\pi}{3}\sin\alpha-\frac{2}{3}\cos\alpha$ B。

$-\frac{\pi}{3}$C。

$\frac{\pi}{6}$D。

$-\frac{\pi}{6}$3、已知 $\tan\alpha=-5$，那么 $\tan\alpha$ 的值为A。

2B。

$\frac{1}{6164}$C。

$-\frac{1}{6164}$D。

$-\frac{2}{3}$4、已知角 $\alpha$ 的余弦线是单位长度的有向线段，那么角 $\alpha$ 的终边（）A。

在 $x$ 轴上B。

在直线 $y=x$ 上C。

在 $y$ 轴上D。

在直线 $y=x$ 或 $y=-x$ 上5、若 $f(\cos x)=\cos 2x$，则 $f(\sin 15^\circ)$ 等于()A。

$-\frac{2}{3}$B。

$\frac{3}{2}$C。

$\frac{1}{2}$D。

$-\frac{1}{2}$6、要得到 $y=3\sin(2x+\frac{\pi}{4})$ 的图象只需将$y=3\sin 2x$ 的图象A。

向左平移 $\frac{\pi}{4}$ 个单位B。

向右平移 $\frac{\pi}{4}$ 个单位C。

一、选择题1.sin(1560)-的值为（ ）A 12-B 12C 32-D 322.如果1cos()2A π+=-，那么sin()2A π+=（ ）A 12-B 12C 32-D 323.函数2cos()35y x π=-的最小正周期是 （ ） A 5π B 52π C 2π D 5π4.轴截面是等边三角形的圆锥的侧面展开图的中心角是 ( )5.A3π B 23π C π D 43π 5.已知tan100k =，则sin80的值等于 （ ）A21k k+ B 21k k-+C21k k + D 21k k+- 7.下列四个函数中，既是(0,)2π上的增函数，又是以π为周期的偶函数的是（ ）A B |sin |y x = B sin y x = C cos y x = D |c o s |y x= 8.已知tan1a =，tan 2b =，tan 3c =，则 （ ）A a b c <<B c b a <<C b c a <<D b a c << 9.已知1sin()63πα+=，则cos()3πα-的值为（ ） A 12 B 12- C 13D 13-10.θ是第二象限角，且满足2cos sin (sin cos )2222θθθθ-=-，那么2θ是 （ ）象限角A 第一B 第二C 第三D 第一或第三11.已知()f x 是以π为周期的偶函数，且[0,]2x π∈时，()1sin f x x =-，则当5[,3]2x ππ∈时，()f x 等于( ）A 1sin x +B 1sin x -C 1sin x --D 1sin x -+12.函数)0)(sin()(>+=ωϕωx M x f 在区间],[b a 上是增函数，且M b f M a f =-=)(,)(，则)cos()(ϕω+=x M x g 在],[b a 上 （ ）A 是增函数B 是减函数C 可以取得最大值MD 可以取得最小值M -13．已知cos tan 0θθ⋅<，那么角θ是 （ ）Ａ．第一或第二象限角 Ｂ．第二或第三象限角 Ｃ．第三或第四象限角 Ｄ．第一或第四象限角 14．已知弧度数为2的圆心角所对的弦长也是2，则这个圆心角所对的弧长是 （ ）A ．2B ．1sin 2 C ．1sin 2 D ．2sin15．为了得到函数2sin(),36x y x R π=+∈的图像，只需把函数2sin ,y x x R =∈的图像上所有的点A ．向左平移6π个单位长度，再把所得各点的横坐标缩短到原来的31倍（纵坐标不变）B ．向右平移6π个单位长度，再把所得各点的横坐标缩短到原来的31倍（纵坐标不变）C ．向左平移6π个单位长度，再把所得各点的横坐标伸长到原来的3倍（纵坐标不变） D ．向右平移6π个单位长度，再把所得各点的横坐标伸长到原来的3倍（纵坐标不变）16．设函数()sin ()3f x x x π⎛⎫=+∈ ⎪⎝⎭R ，则()f x （ ） A ．在区间2736ππ⎡⎤⎢⎥⎣⎦，上是增函数B ．在区间2π⎡⎤-π-⎢⎥⎣⎦，上是减函数 C ．在区间84ππ⎡⎤⎢⎥⎣⎦，上是增函数D ．在区间536ππ⎡⎤⎢⎥⎣⎦，上是减函数17．函数sin()(0,,)2y A x x R πωϕωϕ=+><∈的部分图象如图所示，则函数表达（ ）A ．)48sin(4π+π-=x y B ．)48sin(4π-π=x y C ．)48sin(4π-π-=x y D ．)48sin(4π+π=x y18． 函数sin(3)4y x π=-的图象是中心对称图形,其中它的一个对称中心是 ( )A ．,012π⎛⎫-⎪⎝⎭ B ． 7,012π⎛⎫- ⎪⎝⎭ C ． 7,012π⎛⎫⎪⎝⎭ D ． 11,012π⎛⎫⎪⎝⎭19．已知()21cos cos f x x +=，则()f x 的图象是下图的 ( )A B C D20．定义在R 上的偶函数()f x 满足()()2f x f x =+，当[]3,4x ∈时，()2f x x =-，则 （ ） A ．11sincos 22f f ⎛⎫⎛⎫< ⎪ ⎪⎝⎭⎝⎭ B ．sin cos 33f f ππ⎛⎫⎛⎫> ⎪ ⎪⎝⎭⎝⎭C ．()()sin1cos1f f <D ．33sincos 22f f ⎛⎫⎛⎫> ⎪ ⎪⎝⎭⎝⎭21.已知)0)(sin()(>+=ωϕωx x f 的最小正周期为π，则该函数的图象（ ） A ．关于点)0,3(π对称 B ．关于直线4π=x 对称C ．关于点)0,4(π对称D ．关于直线3π=x 对称22.若函数()2sin()f x x ωϕ=+，x ∈R （其中0ω>，2ϕπ<）的最小正周期是π，且(0)3f =，则（ ）A ．126ωϕπ==，B ．123ωϕπ==， C ．26ωϕπ==， D ．23ωϕπ==，二、填空题 1.函数tan()3y x π=+的定义域为___________。

高一数学必修四《三角函数》测试题班级： 姓名：一、选择题：本大题共10小题，每小题5分，共50分。

在每小题给出的四个 选项中，只有一项是符合题目要求的。

1、 化简sin6000的值是（）D.2、若角 的终边过点（sin30o , —cos30o ），则sin 等于（）5、要得到函数 y=cos （— —）的图象，只需将 y=sin ”的图象 2 42A.向左平移一个单位2B.同右平移一个单位27cos ——cos （ 5C.向左平移 6、下列不等式中, 13 A. tan ——4一个单位4正确的是（. 13 tan 一 5 D.向右平移一个单位4B. sin — cos （一）5 7）8、函数y |tanx|的周期和对称轴分别为（）B.3、已知-sn ——2cos —5,那么tan 的值为（）3sin 5cos23A. — 2B. 2C.—164、下列函数中，最小正周期为兀的偶函数是（）A.y=sin2xB.y=cos —C .sin2x+cos2x D.23 16D. y=cos2xC. sin （九一1）＜sin1o D.D.23kA.,x ——(k Z) 2C. , x k (k Z)B. — ,x k (k Z) 2kD. -,x —(k Z) 2 2则f (竺_)的值等于()4D. f(x) 2sin(2 x —)6二、填空题：本大题共4小题，每小题 11、与 20020终边相同的最小正角是12、设扇形的周长为8cm,面积为4cm 2,则扇形的圆心角的弧度数是2, 、13、函数 y f(cosx)的定义域为 2k -,2k— (k Z), 63则函数y f(x)的定义域为. 14、给出下列命题：5①函数y sin(5— 2x)是偶函数；2②函数y sin( x 1)在闭区间［一,一］上是增函数；42 2 5③直线x 一是函数y sin(2x ——)图象的一条对称轴；84④将函数y cos(2x ―)的图象向左平移 一单位，得到函数 y cos2x 的图象; 33其中正确的命题的序号是：、. ............... 一， 一，,39、设f(x)是定义域为R,最小正周期为— 2的函数，若f (x) cos x( sinx(0x 0) )A.1B. _22C.010、已知函数f(x)Asin( x )(A 0,.则函数f(x)的解析式为( A. f(x) B. f(x) 1 2sin( —x2 12sin(-x2 6)C. f(x) 2sin(2x5分，共20分。

必修4三角函数综合测试题一、选择题1.若点A(x , y)是600°角终边上异于原点的一点，贝U X 的值是( )X A. _2 3 B •-^C •-D•-2. 已知角a 的终边经过点 (—4,3)，贝U cos a =()4 3 小34 A .5 B . ■ C5• — 5D —5 03 .若 |cos0|= cos 0, |tan 0|= — tan 0,则㊁的终边在()A •第一、三象限B .第二、四象限C .第一、三象限或x 轴上D .第二、四象限或 x 轴上4.如果函数f(x)= sin(劇0(0< 0<2n 的最小正周期是 T ,且当x = 2时取得最大值，那么()nA . T = 2, 0= 2B . T = 1 , 0= nC . T = 2,6 .已知a 是实数，而函数f(x)= 1 + asinax 的图象不可能是 … —2sin — cos 0“士 丄，若 tan 0= 2,则 sin 0+2cos 的值为(0= nnD . T = 1 , 0= 25.若 sin (n —x ) = -- 2，且 n<<2n,则 x 等于(A*4 nB.6nof nD.^n 67.将函数 nA.612 t r1 i1 1fr i1iI ” O2 IT -V2^7 XDy = sinx 的图象向左平移 (t(0< ^<2n 个单位长度后，得到 y = sin (x -》 的图象，则©=()5nB.5T 7nC.7n11 n D w8. 2O9. 函数f(x)=tanx1 + cosx的奇偶性是(D•既不是奇函数也不是偶函数A •奇函数B •偶函数C •既是奇函数又是偶函数16. 给出下列命题:十2)是奇函数；②存在实数 X ，使sinx + cosx = 2;③若a, B 是第一象限角且 a < B ，则tan a tan B ；④x=?是函数y = sin (2x +才)的一条对称轴; ⑤函数y = sin (2x + 3)的图象关于点 其中正确命题的序号为 .三、解答题 八 丄、卄..sin n — a +5cos 2 n — a /士17. (10 分)已知万程 sin( a-3n ) 2C0S (a — 4n)求 的值.—sin — a18.(本小题满分12分)已知函数f (x ) = A sin( 3 x + 0 )( A >0, 3 >0, x € R)在一个周期10 .函数 f(x) = V x — cosx 在(0, )内(A •没有零点B •有且仅有一个零点C .有且仅有两个零点D .有无穷多个零点11.已知函数 n f(x)=sin(2x + $)，其中以实数，若f(x)<陀)对x € R 恒成立，且 的单调递增区间是 n A. [ k n —3， k n+ 6】(k € Z) nB. [ k n, k n + 至](k € Z) n 2 nC. [ k n + -Q ， k n — ]( k € Z) nD. [k n — $，k n ]( k € Z)12.函数f(x) = 3sin (2x —扌)的图象为C , ①图象C 关于直线x= 12n 对称；②函数f(x)在区间(器)内是增函数; ③由y = 3sin2x 的图象向右平移个单位长度可以得到图象 C ,其中正确命题的个数是(3B . 1二、填空题(本大题共4小题，每题5分，共20分.将答案填在题中横线上) 13. __________________________________________________ 已知 sin (a + ^) = I , a€ (—扌，°)，则 tan a= ______________________ . 14. 函数y = 3cosx(0<x < n 的图象与直线y =— 3及y 轴围成的图形的面积为 15.已知函数f(x) = sin (3x+册(eO)的图象如图所示，则 (1n ，0)成中心对称. 2前(爭-①函数y =内的图像如图所示，求直线 y = ,；3与函数f (x )图像的所有交点的坐标.n 319. (12 分)已知 f(x) = sin(2x 十百)+ 2, x € R.(1) 求函数f(x)的最小正周期； (2) 求函数f(x)的单调减区间；⑶函数f(x)的图象可以由函数 y = sin2x(x € R)的图象经过怎样变换得到?20. (12分)已知函数y = Asin( 3x+Q (A>0, 3>0)的图象过点 P(1)求函数解析式;⑵求函数的最大值，并写出相应的 x 的值; (3)求使y w 0时，x 的取值范围.点坐标为 (n5).图象与P 点最近的一个最高21. （12 分）已知cos（n- a）=护cos© n+ B），护sin^l^—%）n 一22.函数f i（x）= Asin@ x+ $ ）（A>0, w>0 ,忆|<空）的一段图像过点（0,1），如图所示.y°⑴求函数f i（x）的表达式;⑵将函数y = f i（x）的图像向右平移才个单位，得函数y = f2（x）的图像，求y=f2（x）的最大值, 自变量x的集合，并写岀该函数的增区间.并求出此时且0< a<n,必修4三角函数综合测试题答案二、填空题13. —2羽;14. 3n; 15. 3; 16.三、解答题「sin a=—2cos a可知COS a丸.sin a+ 5cos a原式=—2cos a+ sin a—2cos a+ 5cos a3cos a 3= =—4.—2cos a—2cos a —4COS a18. [解析]由图可知，函数f(x)的A= 2 , T=此时f(x) = 2sin 2x + $，又f nn = 2，n得sin -4 = 1，二$ = 2n n+*，n€ 乙•-f(x) = 2sin 2x +2门兀+于，即f(x) = 2sin1 n当f (x) ='[3，即2sin ^x+ 4 = “•.3 即sin1 n n 1 n2 n二^x+ 4 = 2k n + —或2X+ ~4 = 2k n + , k€ Zn 5 n二x = 4k n + 7-或x= 4k n —, k€ Z6 6n 5 n二所求交点的坐标为4k n + —，3或4k n +〒，秽3，其中k €乙19.解(1)T=2n= n., n 小n 〜 3 n ⑵由2k n+ W 2x+ 6W 2k n+ y,w n , 2 nk ①，得k n+ 6W x< k n+-^ , k€Z.所以所求的单调减区间为[k n+ n，k n+ 2n ](k^Z).n 3 n 3⑶把y= sin2x的图象上所有点向左平移石个单位，再向上平移2个单位，即得函数f(x)= sin(2x+孑)+ ?的图象.20.解(1 )由题意知T= n —12=4，「T=n.一、选择题1. C;2. D;3. D;4. A;5. B6 . D; 7. D ; 8 . C; 9. A; 10. B11 . C; 12. C 17.解'.Sin( a—3 n = 2cos( a—4 n , .「一sin(3 —o) = 2cos(4 —sin( —a)= 2cos(—a).①④2n 1=4 n，. • 3 =3, col x+A =」2 4 22 n . n n , / … n •'•w= T = 2，由3彳2 + $= 0,得 $=—6，又A = 5 ,「y = 5sin( 2x—6).n n n(2)函数的最大值为 5,此时 2x —6 = 2k n+ 2(k^Z).^x = k n+.⑶-.5sin(2x — n) < 0,/-2k n- n 2x —孑 2k n k^Z).5 n^ ,. , n•'k n —12三 x < kn + ^^(k ^Z).n3(2— a )= 2cos(2 n + B )，即 sin a= 2sin pCD3n穆3sin (g — a) = — ,2sin (2 + B )，即.3cos a= 2cos p ②①2 + ② 2得，2 = sin 2 a+ 3COS 2 a 又 Sin 2 a + COS 2 a= 1，—COS 2 a=「COS a= ±2 ■ 又•「aq O , n ，—a= 4，或 a= 4 n⑴当 a= n 时，COS a=¥，COS P=^3COS a=^23，又 贰(0，5 n ，亠「 又Bq o , n) ••• =百.综上,n n 3 n a= 4， 3= 6，或 a = ~4， 3= y.、.nT2.将y = A Sin2 x 的图像向左平移 p ，n n n得 y = A sin(2 x + $ )的图像，于是 $= 2x 巨=g.将(0,1)代入 y = A sin 2x +g ，得 A = 2.,, n故 f 1(x ) = 2sin 2x + y .n nn⑵ 依题意，f 2(x ) = 2sin 2 x — -4 + — =— 2cos 2x + y .n• y = f 2( x )的最大值为 2.当 2x + 百=2k n + n (k € Z),即 x = k n+冷2(k ^ Z)时，y max = 2, x 的取值集合为 x | x = k n + ， k €ZT y = cos x 的减区间为 x € [2 k n, 2k n + n ] , k € Z ,n• f 2( x ) = — 2cos(2 x + )的增区间为6n{x |2 k n< 2x + W 2k n + n, k € Z},6再小n5 n解得{x | k n — "W x < k n + 12, k € Z},⑵当aCOSa #，COS B=W cOS a=—今, 21.解 cos (nn , ;-3= 6.5n2n 22. （1）由题图知，T =n ，于是3n• f2（x ） =-2COS（2x +石）的增区间为x€ [ k n —12, k n + 筈],k € 乙。

兀兀兀兀(cos ------ sin ——)(cos — + sin ——)12 12 1212D.4、1 3 若 sin(^ +A)=- —,则cos (―)的值是 V32 A 、 11 — B 、一 C 、2 2D 、 5、 函数 f(x)=l-二.已知xw B. -1 2 C. 1 20 j ,sin(兀-x)=-1,则 tan 2x 等于( A.Z 24 B ・丄7 .已知 sin(兀 +a)= 1,则 cos 3 3兀 --a 等于A.-1 B. 1 3 c.-晅 3 A.-i 3D. i5必修4三角函数单元测试题一、选择题B.--28 .已知 tan 0=2,则 sin 2d+sin Qcos d-2cos 2Q 等于( C. -14 JT9.函数y = 2sin （2x + —）的最小正周期（氏4c .1 —D.2 1 22. &是第四象限角，tancif =5_12, 贝!] sin a =1 i5 5A.-B.——C. ——D.5513 _131. sin210° =3. B.C. reD.71~213、 函数y =sinl 2x-y I 在区间15、 10、y = （sin x 一 cos x ）? -1 是A.最小正周期为2兀的偶函数B.最小正周期为2兀的奇函数C.最小正周期为兀的偶函数D.最小正周期为兀的奇函数7T11、 给出的下列函数中在（匸）71上是增函数的是（）A 、 y = sin xB 、 y = cos xC 、 y = sin 2xD 、 y = cos 2x12、 已知函数f （x ）=c 〃（x-彳（兀丘砂下面结论错误的是（） A.函数f （x ）的最小正周期为2JI函数f （x ）在区间r 0,£l±是增函数C.函数f （x ）的图象关于直线x=0对称D.函数f （x ）是奇函数7T要得到y = sin （2x-彳）的图象，只要将y = sin2x 的图象（ '1 / /y/A 、向左平移一B 、向右平移一C 、向左平移一D 、向右平移一3 3 6 614.满足函数y = sinx 和y = cosx 都是增函数的区间是（ ）A. [2k7i,2k7T + —], k E ZB. [2k7V + —+ k E Z2 2 C. [2k/v - 7i2kn - —], k e Z D. [2k7V - — ,2k/v] k e Z2 2'7Tn 的简图是（）2A BC D19、贝llsin2 x-cos x =二、填空题16.函数y=Asin( CO x+ (p )( co >0」cp I < 分图象如图，则函数表达式为17.函数/(x) = A/1-2COSX的定义域是18.已知0,0为锐角，且C0S6Z = y COS（Q + 0）= 一昔,贝U COS 0 =1sin x 一cos 兀=一220.已知函数f(x)= A/3sin caxcos cox-c6>52cox(co>0)的周期为巴贝3 二221.给出下列命题：3⑴存在实数&，使sin a cos a (2)存在实数使sin a + cos a23⑶函数y = sin(—7i + x)是偶函数(4)若Q、0是第一象限的角，且a> (3 ,则sin a > sin0 .其中正确命题的序号是 ___________________________________三、解答题22.已知cos 0=-—,冬<0< 兀•5 2(1)求tan 6； (2)求$加2°為％加cos的值.3®flz2+cos223.(15分)已知函数俭)=3$加［丄％ +彳-1/丘尺求: ⑴函数f(x)的最小值及此时自变量x 的取值集合;(2)函数y=W x的图象经过怎样的变换得到函数f(x)=3血［、+了-1的图象?7F(3)若xu 0,—,求函数的最大值。

高中数学必修四三角函数检测题一选择题：本大题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．下列不等式中，正确的是（ ）A ．tan 513tan413ππ< B ．sin )7cos(5ππ-> C ．sin(π－1)<sin1o D ．cos )52cos(57ππ-<2. 函数)62sin(π+-=x y 的单调递减区间是（ ）A ．)](23,26[Z k k k ∈++-ππππB ．)](265,26[Z k k k ∈++ππππC ．)](3,6[Z k k k ∈++-ππππD ．)](65,6[Z k k k ∈++ππππ3.函数|tan |x y =的周期和对称轴分别为（ ）A. )(2,Z k k x ∈=ππ B. )(,2Z k k x ∈=ππC. )(,Z k k x ∈=ππD.)(2,2Z k k x ∈=ππ4.要得到函数x y 2sin =的图象，可由函数)42cos(π-=x y （ ）A. 向左平移8π个长度单位 B. 向右平移8π个长度单位 C. 向左平移4π个长度单位 D. 向右平移4π个长度单位5．三角形ABC 中角C 为钝角，则有 （ ） >cos B B. sin A <cos B C. sin A =cos B D. sin A 与cos B 大小不确定6．设()f x 是定义域为R ，最小正周期为32π的函数，若cos (0)()2sin (0)x x f x x x ππ⎧-≤<⎪=⎨⎪≤≤⎩，则15()4f π-的值等于（ ）A.1 BD.7.函数)(x f y =的图象如图所示，则)(x f y =的解析式为（A.22sin -x yB.13cos 2-=x yC.1)52sin(--=πx yD. )52sin(1π--=x y8．已知函数x b x a x f cos sin )(-=（a 、b 为常数，0≠a ，R x ∈）在4π=x 处取得最小值，则函数)43(x f y -=π是（ ） A ．偶函数且它的图象关于点)0,(π对称B ．偶函数且它的图象关于点)0,23(π对称C ．奇函数且它的图象关于点)0,23(π对称D ．奇函数且它的图象关于点)0,(π对称9．函数]0,[,cos 3sin )(π-∈-=x x x x f 的单调递增区间是（ ）A ．]65,[ππ--B ．]6,65[ππ--C ．]0,3[π-D ．]0,6[π-10. 已知函数sin cos 1212y x x ππ⎛⎫⎛⎫=-- ⎪ ⎪⎝⎭⎝⎭，则下列判断正确的是（ ）A ．此函数的最小周期为2π，其图像的一个对称中心是,012π⎛⎫⎪⎝⎭B ．此函数的最小周期为π，其图像的一个对称中心是,012π⎛⎫⎪⎝⎭C ．此函数的最小周期为2π，其图像的一个对称中心是,06π⎛⎫⎪⎝⎭D ．此函数的最小周期为π，其图像的一个对称中心是,06π⎛⎫⎪⎝⎭11. 若22)4sin(2cos -=-παα，则ααsin cos +的值为（ ） Ａ．27- Ｂ．21- Ｃ．21Ｄ．2712. . 函数23)cos 3(sin cos +-=x x x y 在区间],2[ππ-的简图是（ ）Ａ． Ｂ．二．填空题：本大题共4小题，每小题4分，共16分。